基于投影加权的多能光子计数X线CT全能谱图像重建改进方法
周正东 管绍林 余子丽 张雯雯
(南京航空航天大学核科学与工程系,南京210016)
基于投影加权的多能光子计数X线CT全能谱图像重建改进方法
周正东 管绍林 余子丽 张雯雯
(南京航空航天大学核科学与工程系,南京210016)
为了提高多能光子计数X线CT全能谱重建图像的对比噪声比,提出了一种基于投影加权的图像重建改进方法.首先,针对包含不同对比材料的3种模体进行投影仿真,获得包含泊松噪声和高斯噪声的投影正弦图;然后,从投影正弦图中提取噪声信息,构造关于权重的对比噪声比优化函数;最后,求解出使对比噪声比最优的权重,利用该权重进行投影加权图像重建,并对重建图像进行评估.实验结果表明:与当前仅考虑泊松噪声的基于投影加权的图像重建方法相比,对于含钙材料的模体,利用改进方法可明显提高重建图像的对比噪声比;对于含碘材料和等效软组织材料的模体,利用改进方法重建的图像对比噪声比则无显著统计差异.
光子计数;X线CT;投影;加权;图像重建
不同材料对X线的衰减特性不同,透射出的X线份额也不同.透射X线同时携带材料及入射X线能量的信息.基于投影加权的多能光子计数X线CT图像重建方法充分利用这些信息,通过赋予各能量段投影较优的权重来重建全能谱图像,有利于改善图像质量[1].Giersch等[2]对基于投影加权的多能光子计数X线CT全能谱图像重建方法进行了初步研究,实验结果表明利用该方法可获得对比噪声比良好的全能谱图像;Choi等[3-8]对该方法的有效性进行了进一步验证.然而,这些方法仅考虑了成像系统中泊松噪声的影响,未考虑成像系统中存在的其他噪声源(如探测器元器件的电子噪声、探测器读出电路的读出噪声等).
本文提出了一种基于投影加权的多能光子计数X线CT全能谱图像重建改进方法.从包含多种噪声的投影正弦图中直接提取噪声信息,利用提取的噪声信息及探测光子数的差异,构造关于权重的对比噪声比函数,求解出对比噪声比最优时的权重,并利用该权重进行投影加权图像重建.分别构建了包含等效软组织、钙和碘3种对比材料的3种模体,通过仿真获得包含泊松噪声和高斯噪声的投影正弦图,利用提出的改进方法重建图像并进行评估.
1 图像重建方法
1.1 基于投影加权的图像重建方法
图1为某扫描角度下透射光子探测示意图.图中,Ii0表示多能光子计数X线CT在某一旋转角度下能量段i内发射的X线光子数,该X线穿过衰减系数分别为μ1和μ2的背景材料和对比材料后,探测器采集到的光子数分别为Ii1和Ii2,则其期望值差异Si可表示为[2,6]
Si=〈Ii1〉-〈Ii2〉
(1)
式中,〈·〉表示探测光子数的期望值.
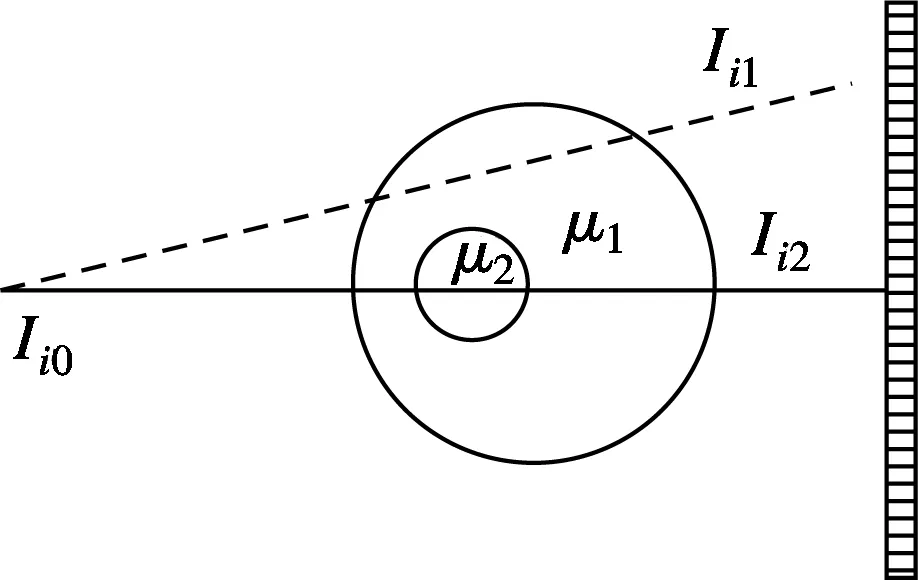
图1 透射光子探测示意图

(2)

(3)
对比噪声比平方最大时的权重为[9-10]
(4)
将上述权重赋予各能量段投影,获得总的探测输出信号,即由光子计数探测器获得的总投影为[9]
(5)
式中,M为能量段的数目;Ii,Ii0分别为能量段i的透射光子计数和入射光子数.利用滤波反投影算法对总投影lp进行重建,即可获得全能谱图像.
1.2 基于投影加权的图像重建改进方法
利用X线对模体扫描,由探测器对透射X线信号进行采集,通过相应电子电路传输处理后的信号中包含多种噪声,主要为与X线相关的噪声,包括X线光子数随机变化引起的噪声、X线进行光电转换时产生的噪声(由康普顿散射、脉冲堆积效应等原因导致)等,这些噪声服从泊松随机分布,称为泊松噪声;此外,还存在与X线无关的噪声,如成像系统中探测器单元的电子噪声、探测器读出电路的读出噪声等,这部分噪声的幅度服从高斯概率密度分布,称为高斯噪声.
由于CT成像过程中存在多种噪声,因此,从投影正弦图中直接提取噪声信息构造关于权重的对比噪声比函数进行图像重建,可以提高重建图像的质量.提取噪声的具体方法为:在包含多种噪声的正弦图中选取一定大小且相对均匀的矩形区(如图2中的矩形区),利用该矩形区内数据的标准差σ来表示正弦图的噪声水平,σ的计算公式为
(6)

图2 投影正弦图
对于由各探测路径下所有扫描角度的投影数据构成的投影正弦图,若考虑其存在的泊松噪声和高斯噪声,则该路径下最终获得的投影信号y可表示为[11]
y=yp+yg
(7)
式中,yp为透射X线被探测器采集前受泊松噪声影响的光子计数;yg为受高斯噪声影响的光子计数.
根据泊松分布可得[11]
(8)
式中,λ为泊松分布的期望.若受泊松噪声影响后的光子又被高斯噪声污染,设该高斯噪声的期望和方差分别为r和δ2,且该高斯噪声为高斯白噪声(即r=0),则最终的投影信号y服从[11]
(9)
从上述投影信号中直接获取噪声信息用于进行对比噪声比的计算.令提取的能量段i投影正弦图的噪声为σi,则对比噪声比的平方可表示为[9]
(10)
式(10)与式(3)的区别在于噪声模型不同.改进方法与基于图像域的加权图像重建方法[9]类似,但是噪声水平的计算域不同,前者是在投影正弦图中计算噪声水平,而后者是在各能量段的重建图像中计算噪声水平.对式(10)求导取极值,可得归一化优化权重为[9]
(11)
将上述权重赋予各能量段的投影后得出总投影,利用滤波反投影算法对总投影进行重建,即可获得全能谱图像.
2 对比材料
运用Geant4软件对多能X线探测进行仿真,以获取多能量段的投影.其中,光子计数探测器的能量阈值设置为58.5和86.5keV,即透射光子被分成3个能量通道采集.受照模体设计为2个半径和位置不同的圆柱状物体,其截面如图3所示.2个圆柱体内分别填充不同X线衰减性质的材料,大圆柱体内填充的是等效脂肪组织材料(即背景材料),小圆柱体内填充的材料为对比材料.为了分析不同材料间的对比差异,内部小圆柱体依次填充设定3种对比材料:等效软组织材料、含碘材料和含钙材料.圆柱体位置、半径和组成材料见表1.

图3 圆柱体模体截面图

材料分类中心坐标/mm半径/mm材料组成密度/(g·cm-3)背景材料(0,0)100C5H8O20.95等效软组织材料(0,50)2514.8%C+11%H+74.2%O1.10含碘材料(0,50)251.2%I+98.8%H2O1.00含钙材料(0,50)2522.5%Ca+20.4%C+9.4%H+47.7%O1.60
通过仿真获得的各能量段投影服从泊松分布.在此基础上,利用normrnd函数添加服从高斯分布的噪声,设置高斯分布的标准差为5.在包含各对比材料的情况下,分别采用基于投影加权的重建方法(以下简写为原方法)和本文提出的改进方法进行图像重建,具体的实验分组情况见表2.由于添加的噪声具有随机性,同组情况(相同的对比材料和重建方法)下多次重建的多幅图像仍存在差异,因此对每一组情况均重复进行实验,获取20次重建结果,并计算得到相应的重建图像对比噪声比.运用统计分析软件SPSS对对比噪声比样本进行统计分析,并假定显著性水平α=0.05.

表2 图像重建分组
3 实验结果与分析
对于表2中的6个实验分组,单次图像重建的结果如图4所示.由图可知,基于2种方法的重建图像难以通过视觉直观评价,同时由于添加的噪声具有随机性,难以根据单次重建结果的优劣来评价方法的优劣程度.

(a) A1

(b) A2

(c) A3

(d) B1

(e) B2

(f) B3
为了客观评价重建图像的质量,对于上述6个实验分组,分别进行20次重复实验,获得的对比噪声比样本值如图5所示.从图中可以看出,各组对比噪声比样本值均存在一定的波动性.当对比材料为等效软组织材料和含碘材料时,2种方法重建图像的对比噪声比样本值差别较小;当对比材料为含钙材料时,对应样本值之间差别明显.
为了分析原方法与改进方法所得图像的对比噪声比样本间的统计学差异,运用SPSS软件对配对样本进行T检验.根据对比材料,将对比噪声比样本分成3对:配对样本(SA1,SB1)、配对样本(SA2,SB2)和配对样本(SA3,SB3), 其中,SA1,SB1,SA2,SB2,SA3,SB3分别表示A1, B1, A2, B2, A3, B3情况下重复进行20次图像重建实验获得的对比噪声比样本.

(a) A1和B1

(b) A2和B2

(c) A3和B3
对配对样本进行T检验需要预先确定配对的2组样本间差值是否服从正态分布.为此,利用SPSS软件对配对样本进行正态性检验.当样本量较大(>2 000)时,Kolmogorov-Smirnov检验的结果较好;反之则Shapiro-Wilk检验的结果较好[12].本文中样本量为20,因此,以Shapiro-Wilk检验的结果作为评价标准,实验结果如表3所示.由表可知,3种情况下Shapiro-Wilk检验的概率值p分别为0.637,0.507和0.516,均大于显著性水平α,说明配对样本间的差值均服从正态分布[13],因此,可以采用T检验对总体参数进行估计.
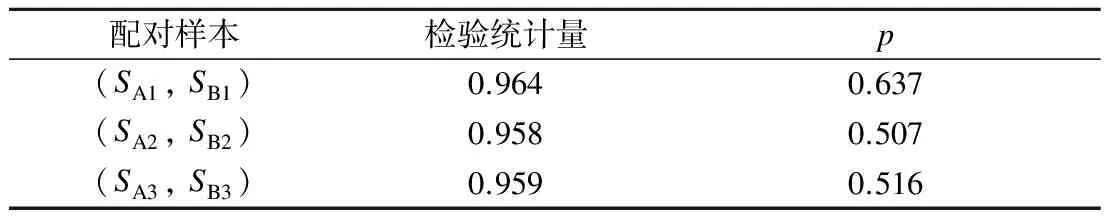
表3 配对样本正态性检验结果
运用SPSS软件进行配对样本T检验.表4给出了配对样本的均值、标准差及均值的标准误差.由表可知,利用改进方法进行图像重建获得的对比噪声比样本的相对均值波动程度以及抽样误差均与原方法所得结果相近.当对比材料为等效软组织材料和含碘材料时,2种方法重建图像的对比噪声比均值没有显著差别;当对比材料为含钙材料时,均值差别较明显,但该差别是否具有统计显著性需进行进一步分析判断.
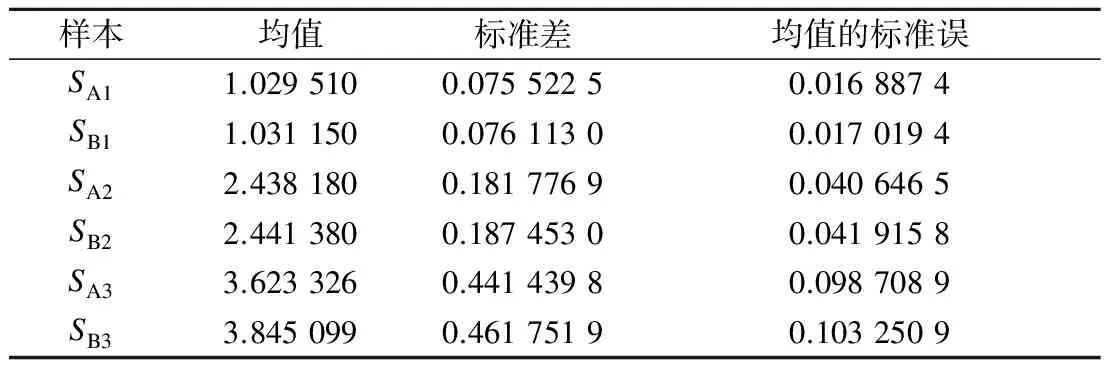
表4 2种方法重建图像对比噪声比样本统计量
表5为配对样本的相关系数及其检验概率值.由表可知,3对样本的相关系数均为正,并且概率值均小于0.05,表明利用2种方法重建的图像对比噪声比样本的线性相关程度较高.
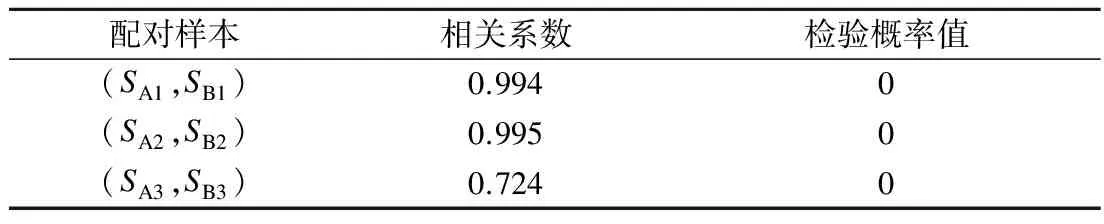
表5 2种方法重建图像对比噪声比样本的相关系数
表6给出了配对样本T检验的结果.由表可知,对于配对样本(SA1,SB1)和(SA2,SB2),双侧概率值分别为0.355和0.451,均大于显著性水平α,表明利用2种方法重建的图像对比噪声比之间不存在显著性差异,即对比材料为等效软组织材料和含碘材料时,利用改进方法重建的图像对比噪声比与原方法所得结果没有显著差别.对于配对样本(SA3,SB3),双侧概率值为0.008,小于显著性水平α,表明利用2种方法重建的图像对比噪声比之间存在显著差异, 结合表6中配对样本(SA3,SB3)差的均值可知,对比材料为密度较大的含钙材料时,利用改进方法重建的图像对比噪声比较大,重建图像的质量较高.

表6 2种方法重建图像对比噪声比样本的配对T检验结果
4 结语
基于投影加权的多能光子计数X线CT图像重建方法利用透射X线包含的信息,通过赋予各能量段投影较优的权重,获得全能谱重建图像,对提高全能谱重建图像质量具有积极意义.目前,基于投影加权的图像重建方法在构造权重优化函数时仅考虑了成像系统中的泊松噪声,而未考虑其他噪声来源.针对该问题,本文提出从投影正弦图中直接提取噪声信息,构造关于权重的对比噪声比优化函数,获得最优权重,进行图像重建,并对重建图像性能进行评估.实验结果表明,与仅考虑泊松噪声的基于投影加权的图像重建方法相比,当对比材料为含钙材料时,利用改进方法可提高重建图像的对比噪声比.投影正弦图包含成像过程中的各种噪声,改进方法从投影正弦图中直接提取噪声信息,能准确地反映噪声的实际情况,在一定程度上有利于改善全能谱重建图像的质量.下一步的研究工作为,在实际成像条件下对该改进方法进行分析与评估,并开展多能光子计数X线CT在物质识别方面的研究.
References)
[1]郝佳, 张丽, 陈志强,等. 多能谱 X 射线成像技术及其在CT中的应用[J]. CT 理论与应用研究, 2011, 20(1): 141-150. Hao Jia, Zhang Li, Chen Zhiqiang, et al. Multi-energy X-ray imaging technique and its application in computed tomography[J].CTTheoryandApplicationsResearch, 2011, 20(1):141-150. (in Chinese)
[2]Giersch J, Niederlöhner D, Anton G. The influence of energy weighting on X-ray imaging quality[J].NuclearInstrumentsandMethodsinPhysicsResearchSectionA:Accelerators,Spectrometers,DetectorsandAssociatedEquipment, 2004, 531(1): 68-74. DOI:10.1016/j.nima.2004.05.076.
[3]Choi Y-N, Lee S-W,Cho H-M, et al. The effect of photon energy weighting on X-ray imaging based on a photon counting detector[J].JournaloftheKoreanPhysicalSociety, 2011, 59(5):3114-3119. DOI:10.3938/jkps.59.3114.
[4]Lee S-W, Choi Y-N, Cho H-M,et al. The effect of energy weighting on X-ray imaging based on photon counting detector: A Monte Carlo simulation[J].PhysicsofMedicalImaging, 2012, 8313(2): 83135M-1-83135M-6. DOI:10.1117/12.910845.
[5]Choi S-H, Lee S-W, Choi Y-N,et al. Projection-based energy weighting on photon-counting X-ray images in digital subtraction mammography: A feasibility study[J].PhysicsofMedicalImaging, 2014, 9033(9): 163-171. DOI:10.1117/12.2043035.
[6]Berglund J, Johansson H, Maack H I, et al. Energy weighting improves the image quality of spectral mammograms: Implementation on a photon-counting mammography system[C]//ProceedingsofSPIEMedicalImagingofMedicalImaging. San Diego, CA, USA 2014:90331E. DOI:10.1117/12.2042238.
[7]Rupcich F, Gilat-Schmidt T. Experimental study of optimal energy weighting in energy-resolved CT using a CZT detector[J].PhysicsofMedicalImaging, 2013,8668(3): 303-311. DOI:10.1117/12.2008439.
[8]Kalluri K S, Mahd M, Glick S J. Investigation of energy weighting using an energy discriminating photon counting detector for breast CT[J].MedicalPhysics, 2013, 40(8): 081923. DOI:10.1118/1.4813901.
[9]Schmidt T G. Optimal “image-based” weighting for energy-resolved CT[J].MedicalPhysics, 2009, 36(7): 3018-3027. DOI:10.1118/1.3148535.
[10]Schmidt T G. CT energy weighting in the presence of scatter and limited energy resolution[J].MedicalPhysics, 2010, 37(3): 1056-1067. DOI:10.1118/1.3301615.
[11]吴治华. 原子核物理实验方法[M]. 北京:原子能出版社, 1997: 1-10.
[12]Nnornadiah M R, Yap B W. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-darling tests[J].JournalofStatisticalModelingandAnalytics, 2011, 2(1):21-33.
[13]何清, 王震坤. 正态性检验方法在教学研究中的应用[J]. 高等理科教育, 2014(4): 18-21,77. DOI:10.3969/j.issn.1000-4076.2014.04.004. He Qing, Wang Zhenkun. Discussion on the application of normality test method in teaching research[J].HigherEducationofSciences, 2014(4): 18-21,77. DOI:10.3969/j.issn.1000-4076.2014.04.004.(in Chinese)
Improved projection-based weighting method for full spectral image reconstruction of multi-energy photon counting X-ray CT
Zhou Zhengdong Guan Shaolin Yu Zili Zhang Wenwen
(Department of Nuclear Science and Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
To improve the contrast-to-noise ratio (CNR) of the full spectral reconstructed image of multi-energy photon counting X-ray computed tomography (CT), an improved projection-based weighting method for image reconstruction is proposed. First, the projection simulation for three kinds of phantom including different contrast materials was carried out and the projection sinograms with Poisson noise and Gaussian noise were obtained. Then,the noise information was extracted from these sinograms, and the CNR optimization function with regard to the weights was formulated. Finally, the optimal weights were figured out and used for the projection-based weighting image reconstruction, and the reconstructed images are evaluated. The experimental results show that, compared with the current projection-based weighting image reconstruction method considering Poisson noise only, the proposed method can obviously improve the CNR of the reconstructed image for the phantom containing contrast material calcium. However, there is no statistically significant difference in CNR for the phantoms containing either iodine or contrast material soft tissue.
photon counting; X-ray computed tomography (CT); projection; weighting; image reconstruction
10.3969/j.issn.1001-0505.2016.06.003
2016-05-22. 作者简介: 周正东(1969—),男,博士,副教授,zzd_msc@nuaa.edu.cn.
国家自然科学基金资助项目(51575256)、中央高校基本科研业务费专项资金资助项目(NP2015101)、江苏高校优势学科建设工程资助项目.
周正东,管绍林,余子丽,等.基于投影加权的多能光子计数X线CT全能谱图像重建改进方法[J].东南大学学报(自然科学版),2016,46(6):1126-1131.
10.3969/j.issn.1001-0505.2016.06.003.
TP391; R318
A
1001-0505(2016)06-1126-06

