考虑冻融的粉质黏土统计损伤本构关系研究

王松鹤，刘奉银，齐吉琳

(1 西安理工大学 岩土工程研究所，陕西 西安 710048；2 北京建筑大学 土木与交通工程学院，北京 100044)



考虑冻融的粉质黏土统计损伤本构关系研究

王松鹤1，刘奉银1，齐吉琳2

(1 西安理工大学 岩土工程研究所，陕西 西安 710048；2 北京建筑大学 土木与交通工程学院，北京 100044)

【目的】 研究冻融作用下土的物理力学性质的变化，构建一种同时考虑荷载效应和冻融循环的损伤模型，为预测冻土地基反复冻融作用下的沉降变形提供理论基础。【方法】 以青藏铁路沿线常见的粉质黏土为研究对象，制备了20组同一目标含水量(16%)和干容重(1.30 g/cm3)的重塑试样，开展了3种正压力(100，200和300 kPa)下的直接剪切试验，剪切变形速率控制为0.8 mm/min。以粉质黏土的抗剪强度数据为基础，采用3种常用的分布函数(正态分布、对数正态分布和Weibull分布)，分析了粉质黏土的抗剪强度分布特征。之后基于Weibull概率密度函数和Lemaitre等效应力原理,推导出三维应力条件下冻土的本构关系；采用Drucker-Prager强度准则反映荷载所致土结构损伤，并选取冻融数次后弹性模量描述冻融循环所致结构损伤，最后提出了一种同时考虑冻融作用和荷载效应的损伤变量，并嵌入冻土损伤本构关系，构建了损伤模型。采用冻融试验数据和三轴剪切试验数据，验证该模型的合理性。【结果】 相比于正态分布和对数正态分布，粉质黏土的强度数据更符合Weibull分布规律，曲线吻合程度和最大偏差均最小。验证试验结果表明，构建的损伤模型的计算结果与试验结果的相关系数均高于0.70，说明该模型能够较好地描述粉质黏土冻融数次后的应力应变特征。【结论】 成功构建了一种同时考虑荷载效应和冻融作用的损伤模型，这为统计损伤本构关系的研究和有效的工程应用提供了参考依据。

粉质黏土；冻融；本构关系；统计损伤；Weibull分布

长期冻融循环严重影响着寒区岩土工程的稳定性，并引发一系列工程问题，比如道路工程翻浆、机场跑道沉降和堤坝裂缝等[1-3]。另外，在深部岩土工程的人工冻结技术使用过程中，冻结壁在开挖过程中及融化后的变形和稳定性越来越引起岩土工作者的关注[4-5]。长期以来，学者对冻胀和融沉两个古老的课题进行了大量研究，积累了丰富的研究资料。然而，冻融后岩土材料性质变化的相关研究开展较晚，已有研究表明[6]，冻融后土的性质会发生明显变化，涉及渗透性增大、强度和模量降低等，这会在寒区工程地基的季节活动层内引起一定附加沉降。目前大量研究集中于冻融后土的物理力学性质方面，主要针对融化状态下土的渗透性、孔隙度等物理指标[7-11]和应力应变特征、强度及其参数等力学性质等的变化[12-15]。

为了合理地预测冻土地基冻融数次后的变形，一些学者采用土的冻融试验，通过研究冻融后弹性模量的变化规律间接预测冻融过程中土的变形过程[12]。此外，从冻融循环作用所致土结构变形的机理出发构建本构关系也是解决冻融数次后冻土地基变形规律的一种方法，Shoop等[16]从春季融化层的破坏出发发现融化后土的变形大部分为塑性变形，包括压缩和剪切两部分，并提出了一种与临界状态类似的Drucker-Prager塑性模型。Zhang等[17]推导出了一种基于临界状态的冻融土力学模型，并将含冰量作为一种标量指标以反映屈服状态的发展。这种方法从试验分析出发很好地反映了冻融后冻土地基的变形规律，但关于冻融循环效应对土的渗透性、孔隙度和力学特性等特征参数的影响及其复杂的变化规律并未在模型中涉及，这在一定程度上限制了模型的发展与推广。另外，冻融过程中，土结构会遭受较大的扰动与重塑，由于冻土结构内部原有细裂纹和结构缺陷的随机分布，也导致土冻融后本构建模仍然有较大难度[18-19]。

鉴于此，本研究尝试从统计损伤的角度出发，选取青藏铁路沿线常见的粉质黏土为研究对象，开展大量的直接剪切试验以分析粉质黏土的抗剪强度的随机分布特征，通过建立合理的损伤变量，构建一种能够综合考虑荷载和冻融循环作用的损伤模型，最后采用室内试验数据对模型的合理性进行验证，以期为损伤模型的研究和有效使用提供参考依据。

1 粉质黏土的强度统计分布特性

1.1 试验方案

试验所用粉质黏土取自青藏铁路沿线，取土深度1.0～2.0 m。粉质黏土的相对密度为2.70，液限和塑限分别为36.8%和20.7%。所取土样的颗粒筛分曲线如图1所示。试验所用土样为重塑圆柱形试样，由湿土压制而成，试样截面积为30 cm2，高度为2.0 cm。目标干容重为1.30 g/cm3，初始含水率为16%，制样前后含水率和干容重误差在1.0%之内。试验在直剪试验仪上进行，试验过程中，正压力(P)分别控制为100，200和300 kPa。每一级正压力下，分别开展20个相同试样的直剪试验，剪切变形速率控制为0.8 mm/min。

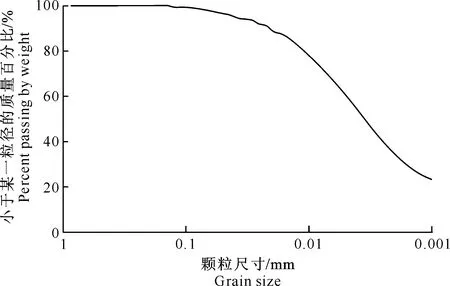
图 1 粉质黏土的颗粒筛分曲线

1.2 试验结果与分析

图2给出了3种正压力下粉质黏土的应力应变曲线。从图2可以看出，在给定的正压力下，应力应变曲线呈现明显的离散性。

图 2 3种正压力(P)下粉质黏土的剪切试验结果

表1列出了粉质黏土的剪切强度和相关的统计分析结果，包括平均值(AVG)、标准差(SD)和变异系数(CV)。从表1可以看出，在正压力为100 kPa情况下，试验数据的离散性较大。

表 1 3种正压力(P)粉质黏土的抗剪强度

1.3 抗剪强度分布特征

为了进一步分析粉质黏土的抗剪强度分布特征，使用SPSS 16.0软件对比了抗剪强度3种常用的统计分布，即正态分布、对数正态分布和Weibull分布，结果如图3所示。一般常用Q-Q图研究样本是否来自于某一特定的目标分布[20]，本研究使用Q-Q图来反映其概率分布。对于正态分布，表1已列出粉质黏土抗剪强度的平均值和均方差，故表2仅给出对数正态分布和Weibull分布的比例参数和形参数。

表 2 不同正压力(P)下粉质黏土抗剪强度对数正态分布和Weibull分布的特征参数

从图3可以看出，Q-Q图中粉质黏土抗剪强度的数据点大部分位于Y=X线附近，表明试验数据与3种常用的统计分布均吻合较好。为了进一步评定3种常用统计分布的预测效果，图4给出了抗剪强度预测值与观测值的偏差与观测值的关系。从图4可以看出，相比于正态分布和对数正态分布而言，Weibull分布预测结果与实测值偏差均较小，大多数数据点集中在偏差为0的虚线附近，在正压力分别为100，200和300 kPa时，其最大偏差分别为4.04,3.28,和-4.94 kPa。这种差别可能与制样过程中含水率和干密度的控制精度有关。

图 3 不同正压力(P)下粉质黏土抗剪强度分布特征的对比

2 考虑冻融作用的冻土统计损伤本构关系探讨

在冻土中原有结构缺陷和微裂隙等导致外荷载作用下均会导致初始损伤扩展和连接，从而弱化冻土的宏观力学性质；与此同时，长期的反复冻融也会对其结构产生复杂影响。如何合理反映冻土在荷载和冻融双重作用下的损伤规律，关键在于选取适宜的损伤变量。对于荷载作用损伤，许多学者选取了微观基准量进行分析[21-22]，由于土体初始损伤的随机性及随机演化，使用常规方法确定的本构关系不能很好地反映随机特征，而概率统计损伤的引入为解决这一问题提供了新思路。

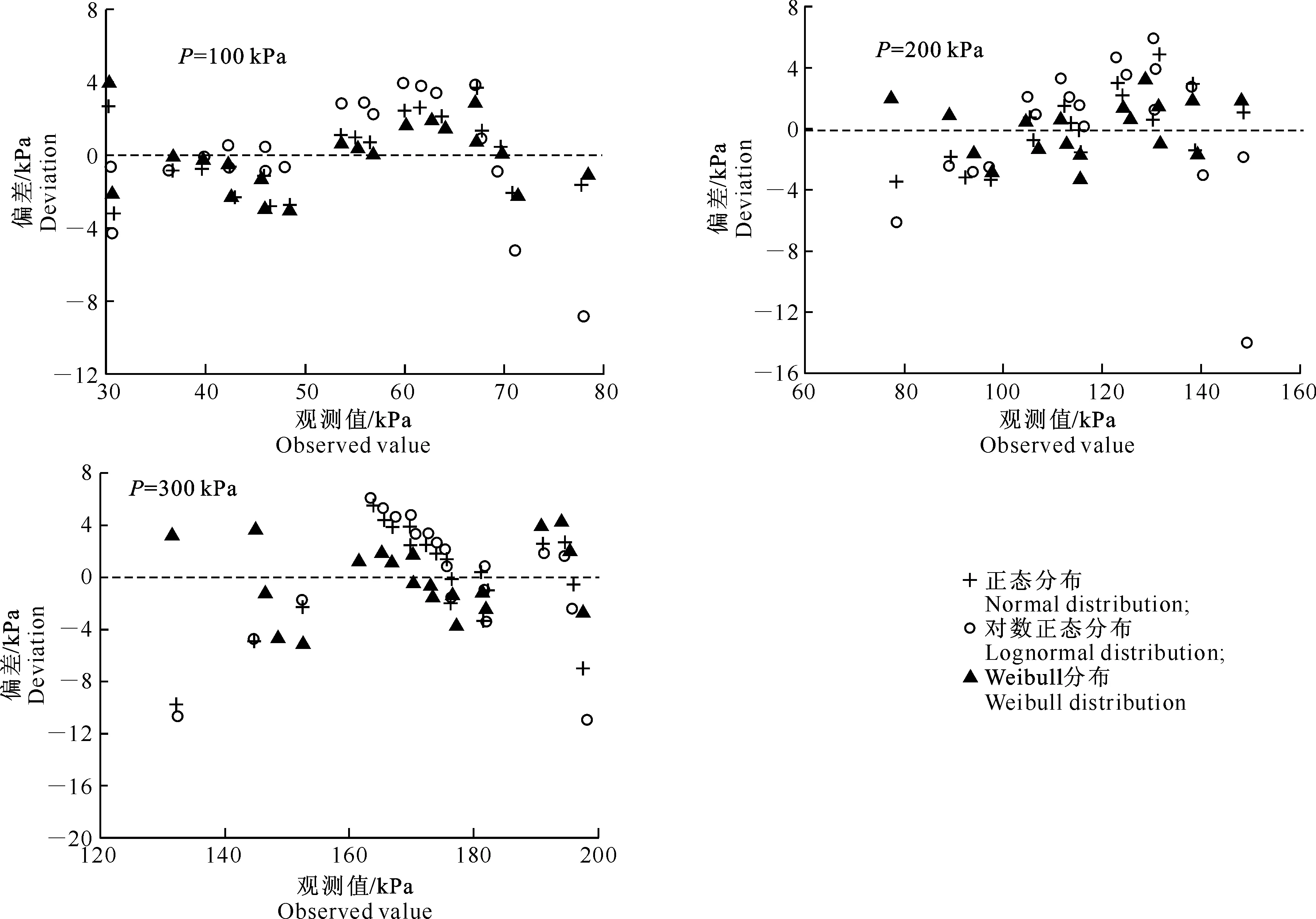
图 4 不同正压力(P)下粉质黏土抗剪强度观测值与预测值偏差

对于岩石和混凝土等岩土材料的强度，大致可以从正态分布、对数正态分布和Weibull分布等概率分布出发分析其随机性。前期试验研究表明，Weibull分布更适宜描述冻结和融化状态下青藏铁路沿线粉质黏土的强度分布规律[18-19]。以微元强度作为随机变量的Weibull概率密度函数，有：

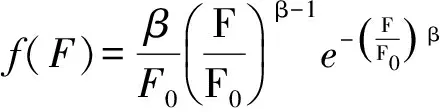
(1)

式中：β和F0均为Weibull分布规律的特征参数，即形参数和比例参数；F为微元体的强度准则。

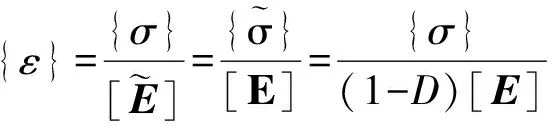
(2)

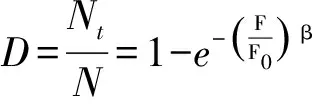
(3)

引入上述损伤变量，可以得到轴对称三轴应力条件下土体的应力应变关系为：

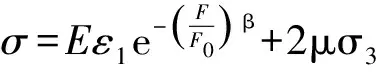
(4)

式中：E为土的弹性模量，ε1为土的轴向应变，μ为土的泊松比，σ3为围压。

以上即是土在荷载作用下的统计损伤本构关系。

对于土体微元，需要给定相应的强度准则F。常规土力学中，目前常用的屈服准则包括Tresca准则、Mises准则、Mohr-Coulomb准则和Drucker-Prager系列准则等[24]。其中Drucker-Prager系列准则简单实用，能合理反映岩土材料的黏聚力和粒间摩擦效应，广泛应用于土力学研究和工程领域。邓楚键等[25]根据光滑刚性条形地基的极限承载力问题对比了Drucker-Prager系列准则的理论结果与精确解发现，平面应变情况下内切圆准则与理论结果较一致。据此，这里引入Drucker-Prager内切圆准则F，以主应力表示为：

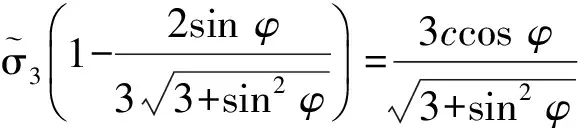
(5)

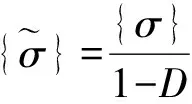
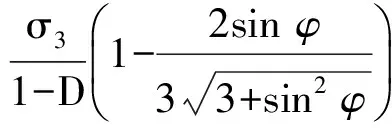
(6)

根据应力应变关系可得：

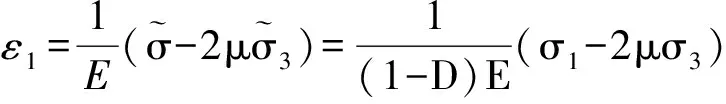
(7)

结合上述两式得：

(8)

根据冻融n次后土的弹性模量En以及土体破坏时的应力σp、应变εp和屈服函数Fp，可求得损伤变量中参数β和F0：

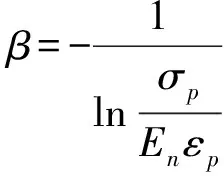
(9)

(10)

对于冻融作用引发的损伤，在研究材料的损伤状态时采用以宏观尺度表示的损伤变量，并以弹性模量这一宏观物理量定义土冻融数次后的损伤变量Dn，有：

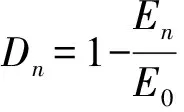
(11)

式中：E0为土未经冻融情况下的弹性模量，En为冻融n次后土的弹性模量。

为了综合反映荷载和冻融的影响，本研究采用文献[26]中冻融与荷载耦合作用下岩石结构损伤发展演化规律的处理方法。首先，采用张全胜等[27]建议的应力等效原理，将冻土的初始损伤状态定义为基准损伤状态，并认为在材料损伤扩展过程中，任取其中两种损伤状态，则材料在第一种损伤状态下的有效应力作用于第二种损伤状态引起的应变，等价于材料在第二种损伤状态下的有效应力作用于第一种损伤状态引起的应变。

其次，假设冻融损伤后的状态定义为第一种损伤状态，冻融受荷引起的总损伤状态作为第二种损伤状态，则冻土材料内部损伤本构关系为：

{σ}=(1-Dm)[E]{ε}。

(12)

Dm=D+Dn-D·Dn。

(13)

式中：Dm为考虑冻融和荷载综合作用的损伤变量；D为考虑荷载作用的损伤变量；Dn为考虑冻融作用的损伤变量；D·Dn为耦合项，反映了冻融循环与荷载对结构损伤的综合作用。

最后，将D和Dn代入总损伤变量公式中，得：

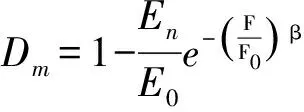
(14)

将上述损伤演化方程代入原本构关系中，得：

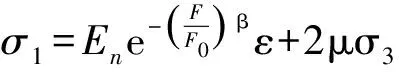
(15)

需要确定的参数包括不同冻融次数下土的弹性模量En、内摩擦角φ、参数β、F0和破坏应变εp。

3 验证试验

根据文献[12]中的试验资料验证上述模型。试验所用粉质黏土取自青藏铁路沿线，其液限和塑限分别为36.8%和20.7%。试样为直径61.8 mm、高125 mm圆柱体试样，初始含水率为17.78%。所制备的黏土试样分为8组，每组5个试样，其中1组不进行冻融循环试验，直接进行三轴剪切试验，确定未经冻融试样的强度指标；其余7组进行不补水冻融试验，随后在围压(σ3)分别为200，400和600 kPa时进行三轴不固结不排水剪切试验，轴向加载速率控制为0.5 mm/min。冻融试验过程中，冻结温度控制为-7.0 ℃，融化温度控制为14.0 ℃，冻融次数(n)分别控制为0，3，10和21。

选取应变为1%对应的偏应力数据，计算粉质黏土冻融数次后的弹性模量[28]。损伤变量Dn的变化过程如图5所示。

图 5 不同围压(σ3)下粉质黏土损伤变量(Dn)随冻融次数的变化

从图5可以看出，土体结构在初始数次冻融循环后发生了明显的结构损伤，而后由于结构裂隙恢复而逐渐趋于稳定。另外，损伤变量Dn随冻融次数的变化较剧烈，在冻融7次后基本趋于稳定。

图6给出了同时考虑荷载效应和冻融作用的损伤变量Dm的变化规律。从图6可以看出，在给定围压条件下，损伤变量与应变发展均呈现出非线性变化特征，且在一定冻融次数后趋于稳定。另外，由于较高压力下土样本身颗粒破碎和重定向等因素影响，故高压力下的损伤变量Dm较低压力大。

图 6 不同围压(σ3)和冻融次数(n)下粉质黏土损伤变量(Dm)的变化

假设泊松比在冻融后变化较小，取为定值0.35。根据文献[12]中所用的剪切试验资料，本研究分析得到不同围压下考虑冻融和荷载耦合影响的本构关系参数如表3所示。

表 3 不同围压(σ3)下考虑冻融和荷载耦合影响的粉质黏土本构关系模型的参数

图7给出了实测的应力应变结果与计算结果的对比。图7表明，计算得到的应力应变结果与实测数据较为接近，大致分布于Y=X线附近，表明计算结果与实测试验结果吻合较好。采用SPSS软件数理统计功能计算了应力应变实测试验结果与计算结果的相关系数，结果见表4。从表4可以看出，模型的计算结果与试验数据的相关系数均高于0.70，说明该模型能够较好地描述粉质黏土冻融数次的应力应变特征。

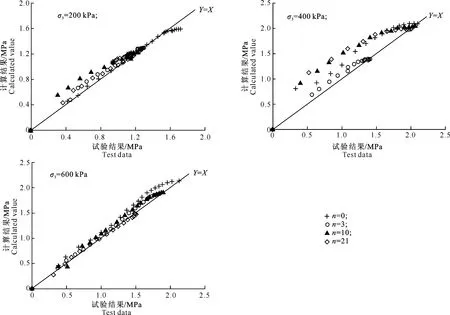
图 7 不同围压(σ3)下粉质黏土应力应变实测数据与计算结果的比较

σ3/kPa冻融次数(n)Numberoffreeze⁃thawcycles0310212000．900．940．770．854000．860．940．850．816000．880．900．900．98

4 结 论

本研究以青藏铁路沿线的粉质黏土为对象，通过大量直接剪切试验测试了其抗剪强度，并分析了其抗剪强度分布特征，结果表明，Weibull分布相比于正态分布和对数正态分布更适用于描述粉质黏土不同荷载水平下的抗剪强度分布规律。

为了反映荷载所致土结构损伤，本研究引入Drucker-Prager强度准则反映土体微元的破坏，推导出了荷载作用下的粉质黏土损伤变量；考虑到冻融数次后土的弹性模量变化，选取宏观指标弹性模量的变化率作为冻融所致结构损伤的基本变量。在综合二者影响基础上，推导出一种同时考虑荷载和冻融综合影响的本构关系。采用冻融试验数据和三轴剪切试验数据，验证了模型的合理性，结果表明，应力应变预测结果与实测数据吻合较好，该本构关系能够比较合理地反映冻融后粉质黏土的应力应变特征。

[1]Qi J L,Sheng Y,Zhang J M,et al.Settlement of embankments in permafrost regions in the Qinghai-Tibet Plateau [J].Norwegian Journal of Geography,2007,61(2):49-55.

[2]Wang S H,Qi J L,Yu F,et al.A novel method for estimating settlement of embankment in cold regions [J].Cold Regions Science and Technology,2013,88:50-58.

[3]Qi J L,Yao X L,Yu F.Consolidation of thawing permafrost considering phase change [J].KSCE Journal of Civil Engineering,2013,17(6):1293-1301.

[4]马 巍,程国栋,吴青柏.青藏铁路建设中动态设计思路及其应用研究 [J].岩土工程学报,2004,26(4):537-540.

Ma W,Cheng G D,Wu Q B.Study and application of idea of dynamic design in Qinghai-Tibet railway construction [J].Chin J Geotech Eng,2004,26(4):537-540.

[5]Wang D Y,Ma W,Wen Z,et al.Study on strength of artificially frozen soils in deep alluvium [J].Tunneling and Underground Space Technology,2008,23(4):381-388.

[6]Qi J L,Pieter A V,Cheng G D.A Review of the influence of Freeze-thaw cycles on soil geotechnical properties [J].Permafrost and Periglacial Processes,2006,17:245-252.

[7]齐吉琳,张建明,朱元林.冻融作用对土结构性影响的土力学意义 [J].岩石力学与工程学报,2003,22(S2):2690-2694.

Qi J L,Zhang J M,Zhu Y L.Influence of freezing-thawing on soil structure and its soil mechanics significance [J].Rock Mech Eng,2003,22(S2):2690-2694.

[8]Viklander P.Permeability and volume changes in till due to cyclic freeze/thaw [J].Canadian Geotechnical Journal,1998,35(3):471-477.

[9]Chamberlain E J,Gow A J.Effect of freezing and thawing on the permeability and structure of soils [J].Eng Geol,1979,13(1/2/3/4):73-92.

[10]Eigenbrod K D.Effects of cyclic freezing and thawing on volume changes and permeabilities of soft fine-grained soils [J].Canadian Geotechnical Journal,1996,33(4):529-537.

[11]Othman M A,Benson C H.Effect of freeze-thaw on the hydraulic conductivity and morphology of compacted clay [J].Canadian Geotechnical Journal,1993,30:236-246.

[12]王大雁,马 巍,常小晓，等.冻融循环作用对青藏黏土物理力学性质的影响 [J].岩石力学与工程学报,2005,24(23):4313-4319.

Wang D Y,Ma W,Chang X X,et al.Physico-mechanical properties changes of Qinghai-Tibet clay due to cyclical freezing and thawing [J].Rock Mech Eng,2005,24(23):4313-4319.

[13]齐吉琳,马 巍.冻融作用对超固结土强度的影响 [J].岩土工程学报,2006,28(12):2082-2086.

Qi J L,Ma W.Influence of freezing-thawing on strength of overconsolidated soils [J].Chin J Geotech Eng,2006,28(12):2082-2086.

[14]Simonsen E,Isacsson U.Soil behavior during freezing and th-awing using variable and constant confining pressure triaxial tests [J].Canadian Geotechnical Journal,2001,38:863-875.

[15]Simonsen E,Janoo V C,Isacsson U.Resilient properties of un-bound road materials during seasonal frost conditions [J].Journal of Cold Regions Engineering,2002,16(1):28-50.

[16]Shoop S,Affleck R,Haehnel R,et al.Mechanical behavior modeling of thaw-weakened soil [J].Cold Regions Science and Technology，2008，52：191-206.

[17]Zhang Y,Michalowski R.Thermal-mechanical constitutive mo-deling for freezing and thawing soils [C]//Jon E,Zufelt.Proceedings of the 10th International Symposium on Cold Regions Development.Anchorage,Alaska,United States:American Society of Civil Engineers,2013:256-267.

[18]Lai Y M,Li S Y,Qi J L,et al.Strength distributions of warm frozen clay and its stochastic damage constitutive model [J].Cold Regions Science and Technology,2008,53:200-215.

[19]Li S Y,Lai Y M,Zhang S J,et al.An improved statistical damage constitutive model for warm frozen clay based on Mohr-Coulomb criterion [J].Cold Regions Science and Technology,2009,57:154-159.

[20]Wilk M B,Gnanadesikan R.Probability plotting methods for the analysis of data [J].Biometrika,1968,55(1):1-17.

[21]赖远明,李双洋,高志华,等.高温冻结黏土单轴随机损伤本构关系及强度分布规律 [J].冰川冻土,2007,29(6):969-976.

Lai Y M,Li S Y,Gao Z H.Stochastic damage constitutive model for warm frozen soilunder uniaxial compression and its strength distribution [J].Journal of Glaciology and Geocryology,2007,29(6):969-976.

[22]宁建国,朱志武.含损伤的冻土本构关系及棍合问题数值分析 [J].力学学报,2007,39(1):70-76.

Ning J G,Zhu Z W.Constitutive model of frozen soil with damage and numerical simulation of the coupled problem [J].Chinese Journal of Theoretical and Applied Mechanics,2007,39(1):70-76.

[23]Lemaitre J,Chaboche J L.Mechanics of solid materials [M].London:Cambridge University Press,1970.

[24]黄文熙.土的工程性质 [M].北京:水利电力出版社,1983.

Huang W X.Engineering properties of soil [M].Beijing:Water Resources and Electric Power Press,1983.

[25]邓楚键,何国杰,郑颖人.基于M-C准则的D-P系列准则在岩土工程中的应用研究 [J].岩土工程学报,2006,28(6):735-739.

Deng C J,He G J，ZhengY R.Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering [J].Chin J Geotech Eng,2006,28(6):735-739.

[26]张慧梅,杨更社.冻融受荷岩石唯象损伤扩展特性探讨 [J].西安建筑科技大学学报(自然科学版)，2010,42(2):300-303.

Zhang H M,Yang G S.Discussion on the enological damage propagation characteristics of rock under freeze-thaw and load conditions [J].J Xi’an Univ Arch Technol(Nat Sci Ed),2010,42(2):300-303.

[27]张全胜,杨更社,任建喜.岩石损伤变量及本构方程的新探讨 [J].岩石力学与工程学报,2003,22(1):30-34.

Zhang Q S,Yang G S,Ren J X.New study of damage variable and constitutive equation ofrock [J].Rock Mech Eng,2003,22(1):30-34.

[28]Lee W J,Bohra N C,Altschaeffl A G,et al.Resilient modulus of cohesive soils and the effect of freeze-thaw [J].Candian Geotechnical Journal,1995,32:559-568.

Statistical damage constitutive model for silty clay after freeze-thaw cycling

WANG Songhe1,LIU Fengyin1,QI Jilin2

(1 Institute of Geotechnical Engineering,Xi’an University of Technology,Xi’an,Shaanxi 710048,China;2CollegeofCivilandTransportationEngineering,BeijingUniversityofCivilEngineeringandArchitecture,Beijing100044,China)

【Objective】 The physical and mechanical properties of soils after freeze-thaw cycling were studied and a constitutive model was built to provide theoretical basis for better predicting settlement of permafrost foundations after cyclic freeze-thaw.【Method】 This study investigated the frequently encountered silty clay along Qinghai-Tibet railway.Twenty remolded samples with identical target water content (16%) and dry unit density (1.30 g/cm3) were produced and used in direct shear tests under three normal stresses (100,200 and 300 kPa),with a shear rate of 0.8 mm/min.Based on the shear strength data of silty clay,the statistical strength characteristics were investigated by comparing three typical statistical distributions including the normal distribution,lognormal distribution and Weibull distribution. The constitutive equation for frozen soils at triaxial conditions was deduced based on a Weibull probability density function and Lemaitre equivalent stress principle.A statistical damage variable incorporating a Drucker-Prager strength criterion was suggested for load-induced structural damage of silty clay while the variation in the elastic modulus was taken as the damage variable for freeze-thaw induced damage.After coupling the two damage variables,a statistical damage constitutive model was proposed for silty clay.The reasonability of the constitutive equation was verified by a series of laboratory freeze-thaw tests and conventional triaxial tests on silty clay.【Result】 The Weibull distribution was more suitable for the strength of silty clay compared with the normal and the lognormal distributions and the predicted curve fit well with test data and the maximum deviation was relatively small.The calculated stress-strain curves agreed in general with test data with correlation coefficient of >0.7.【Conclusion】 A damage constitutive model was proposed by considering both the loading and freeze-thaw effects to provide guidance for further study on statistical damage constitutive model and the effective application in engineering.

silty clay;freeze-thaw;constitutive model;statistical damage;Weibull distribution

时间:2016-10-20 16:37

10.13207/j.cnki.jnwafu.2016.12.031

2015-07-17

国家自然科学基金项目(51408486,41572268)；北京市属高等学校高层次人才引进与培养计划项目(CIT&TCD20150101)

王松鹤(1985-),男, 河北藁城人，讲师，博士，主要从事冻土力学与寒区工程研究。E-mail：wangsonghe@126.com

TU445

A

1671-9387(2016)12-0226-09

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20161020.1637.062.html