广义极值分布序列经验概率的计算
齐哲娴,宋松柏
(1 西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100;2 浙江大学 建筑工程学院,浙江 杭州 310058)
广义极值分布序列经验概率的计算
齐哲娴1,2,宋松柏1
(1 西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100;2 浙江大学 建筑工程学院,浙江 杭州 310058)
【目的】 研究并建立广义极值分布无偏经验概率计算公式,为广义极值分布经验概率的计算提供支持。【方法】 应用次序统计量原理,推导广义极值分布无偏经验概率计算公式,采用统计试验方法将推导的公式与现有的经验频率公式进行对比,对其进行检验,最后以陕北地区12个水文测站的年最大洪峰流量系列为例进行模型应用。【结果】 推导出了便于工程设计应用的广义极值分布经验概率计算公式GEVQG。统计试验和实例应用表明:推导的公式GEVQG和现有经验频率公式Cunnane公式的相对误差和偏差均较小,并且对研究区的拟合效果良好。【结论】 推导的计算公式GEVQG和Cunnane公式均可以作为广义极值分布经验概率计算的优选公式,为工程水文经验概率计算提供了新的选择。
无偏经验频率公式;广义极值分布;洪水频率分析;次序统计量;陕北地区
绘点位置公式也称经验频率公式,是目前适线法确定分布参数和评定各类参数估算方法的依据。从20世纪50年代开始,我国一直沿用数学期望公式进行P-Ⅲ型分布参数适线法估算。武汉大学郭生练等[1]指出:不少人在这种不合适的绘点位置基础上推敲各种适线准则的优劣,或抽取“理想”样本作为比较各种参数估计方法的基准,这显然劳而无功或不太合理。
Hazen[2]最早将经验频率公式应用到水文频率分析中。Weibull[3]以次序统计量频率的数学期望值(E[F(xm)])为依据,建立了数学期望公式。Kimball[4]推荐以次序统计量的数学期望频率(F[E(xm)])为依据建立经验概率公式。Harter[5]指出,经验频率公式选择存在各种混乱和争议的原因在于F[E(xm)]不等于E[F(xm)],并研究推荐使用中值公式。当样本长度小于20时,可以利用Johnson[6]给出的表格查算经验频率;而当样本长度大于20时,可以应用Blom公式[7]。
Gringorten[8]建立了适用于极值Ⅰ型分布的以F[E(xm)]为依据的经验频率公式。Cunnane[9]提出了一个与分布无关的无偏经验概率公式。Arnell等[10]利用概率权重矩法推求了广义极值分布的无偏绘点位置公式,由于数值计算问题该公式仅适用于样本容量小于35的情况,但其也给出了样本容量更大时的近似求解公式。In-na等[11]在Arnell公式的基础上,进一步发展了广义极值分布无偏经验频率公式。Goel等[12]利用概率权重矩法提出了具有偏态系数的广义极值分布经验频率公式。De[13]修正了Gringorten公式。Kim等[14]利用遗传算法推求了广义极值分布的经验频率公式。
郭生练[15]选用湖北省42个测站的年最大流量系列,分析对比了6种线型,发现广义极值分布和P-Ⅲ分布一样都能较好地拟合实测资料。陈兴旺[16]以南昌市年汛期最大降水量为例,采用广义极值分布理论进行拟合,认为该理论分布合理可靠,可以满足实际工程设计的需要。上述研究初步说明,广义极值分布基本适用于我国的水文情势[17],但由于水文情势影响因素的复杂性,不同地区适宜的水文频率和参数估计方法具有一定的差异,而目前我国尚缺乏不同地区水文广义极值分布无偏经验频率计算理论的研究报道。
本研究采用水文统计原理和数值计算方法,研究和推导极值Ⅰ型、极值Ⅱ型和极值Ⅲ型分布无偏经验频率计算公式和求解技术,在Goel和De[12]推荐的概化公式基础上,推导理论上更适合广义极值分布经验概率的计算公式,并与现有的经验频率公式进行对比,利用统计试验优选最佳经验频率公式,最后以陕北地区12个水文测站的洪水资料进行洪水分布参数和设计值推求,以期为研究区水利工程建筑物的设计提供科学依据,并为工程水文经验概率计算提供理论支撑。
1 理论与方法
1.1 广义极值分布[12,18]
广义极值分布(GEV)的定义为:
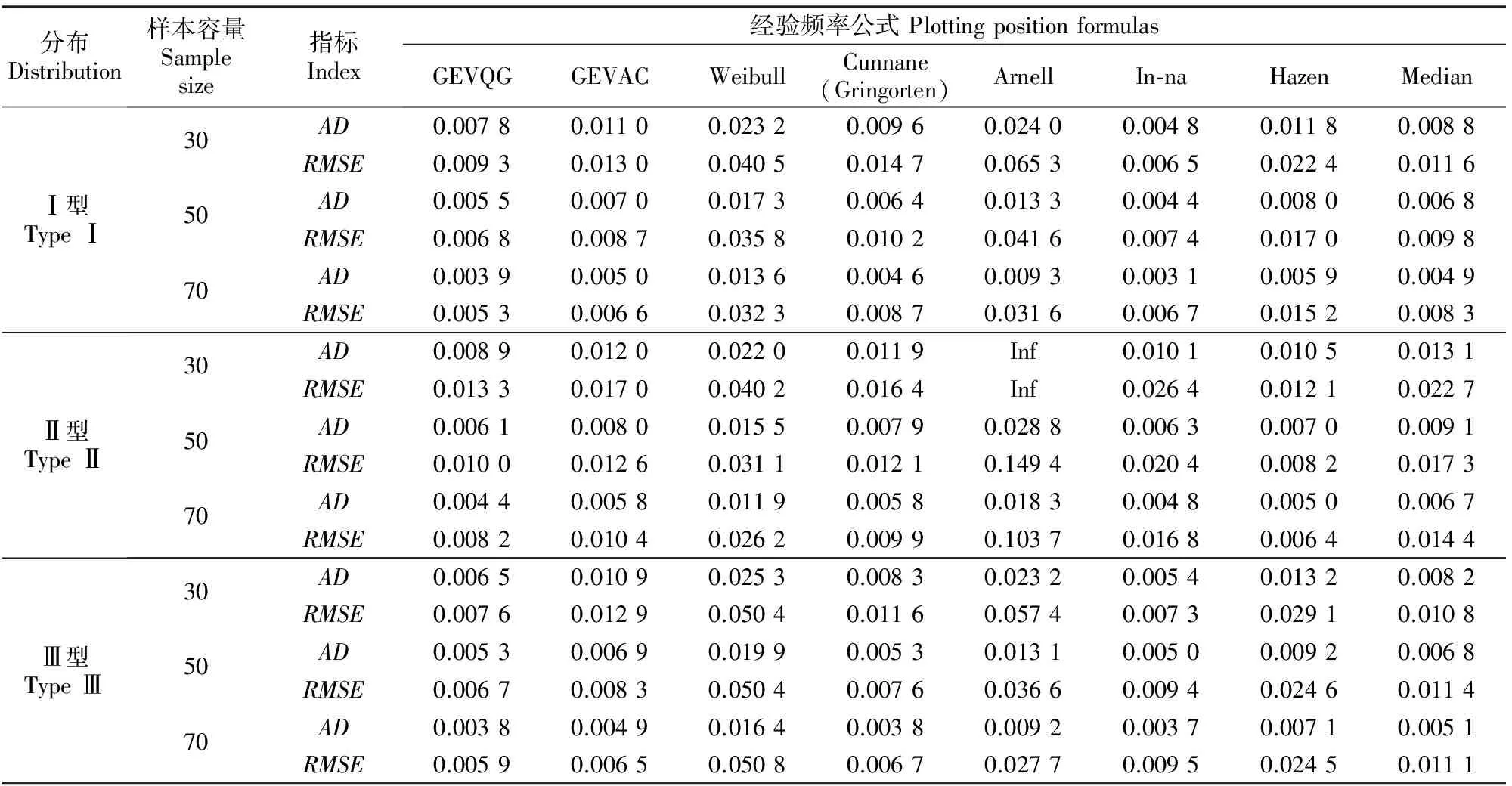
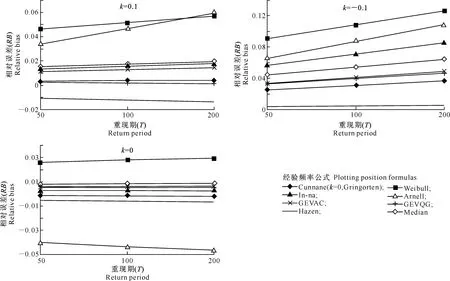
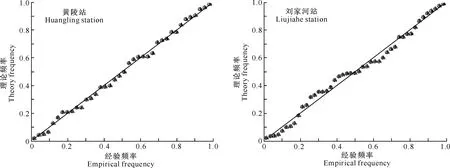
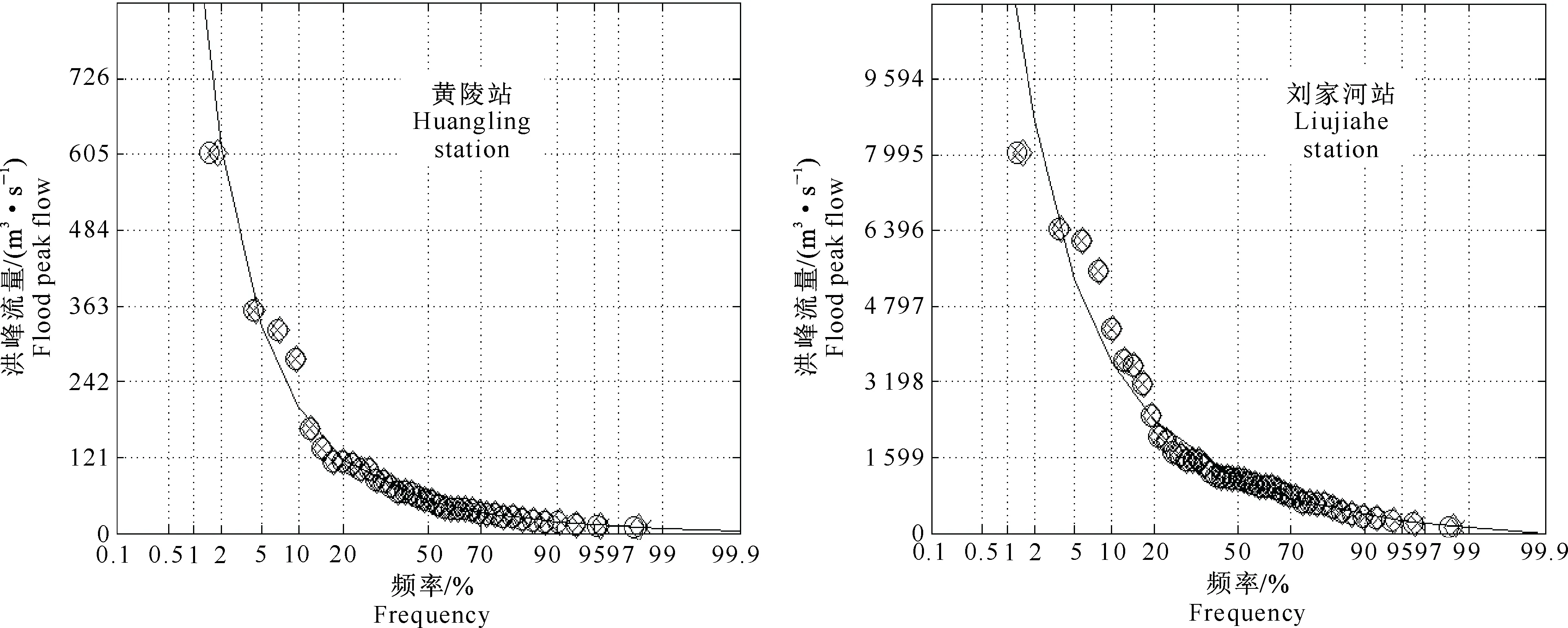
F(x)=P(X exp{-[1-k(x-u)/α]1/k},k≠0; (1) F(x)=P(X exp{-exp[-(x-u)/α]},k=0。 (2) 式中:X为随机变量,u、α和k分别为位置、尺度和形状参数。 广义极值分布分为Ⅰ、Ⅱ、Ⅲ型,即有: 1)k=0时,分布为极值Ⅰ型分布(EV1),也称耿贝尔分布(Gumbel distribution),x的取值范围为-∞ 2)k<0时,分布为极值Ⅱ型分布(EV2),也称弗雷德分布(Frechet distribution),x的取值范围为(u+α/k)≤x<∞;分布曲线的下端有限,上端无限。 3)k>0时,分布为极值Ⅲ型分布(EV3),也称威布尔分布(Weibull distribution),x的取值范围为-∞ 形状参数k与偏态系数Cs的关系见图1。 图 1 广义极值分布形状参数k和偏态系数Cs的关系 形状参数k与偏态系数Cs的关系式为: (3) μ2=Γ(1+2k)-Γ2(1+k); (4) μ3=Γ(1+3k)-3Γ(1+2k)Γ(1+k)+ 2Γ3(1+k),k<0; (5) μ3=-[Γ(1+3k)-3Γ(1+2k)Γ(1+k)+ 2Γ3(1+k)],k>0。 (6) 1.2 广义极值分布次序统计量的数学期望[12,19] 给定样本容量为n的次序化随机观测样本y(1)≤y(2)≤…≤y(n),第m阶次序统计量的概率密度函数为: (7) 式中:F(·)和f(·)分别为样本的分布函数和密度函数。 则y(m)的数学期望为: (8) 由此可得极值Ⅰ型、Ⅱ型、Ⅲ型分布第m阶次序统计量的数学期望依次为: (9) (10) (11) 将式(9)、(10)和(11)分别应用二项级数展开,进行计算后可得: (-1)s[γ+ln(m+s)](m+s)-1, (12) (13) E(y(3m))=-E(y(2m))。 (14) 式中:γ为欧拉常数,γ=0.577 2;s为参数;其他符号意义同前。 1.3 广义极值分布经验概率的计算 以F(E(Xm))作为绘点位置不仅具有良好的理论基础支撑,而且会得到良好的统计性质[1]。因此,广义极值分布第m阶次序统计量y(m)的绘点位置计算公式为: Pm=F[E(y(m))]。 (15) E(y(m))为上述方法推得广义极值分布次序统计量的数学期望。为了便于工程设计的使用,通过综合归纳,多数经验频率公式可以概化为下列通式: (16) nPm-m=a+bPm。 (17) 式中:a和b为未知系数。 式(17)右边是Pm的线性函数,对于给定的样本容量n和偏态系数Cs(或形状参数k),(nPm-m)与Pm之间存在线性关系,应用式(12)、(13)、(14)计算广义极值分布第m阶次序统计量的数学期望E(y(m))。可令y=E(y(m)),应用下式计算Pm,然后利用MATLAB软件将(nPm-m)和Pm进行回归分析,即可得到a和b的值。 (18) 本研究中形状参数k取-0.3 ~1.5,k计算步长为0.1。n取10~100,n计算步长为5。参照公式(3)中k与Cs的关系,经过回归分析计算后,广义极值分布经验概率公式有: (19) 将式(19)命名为GEVQG公式。 为了比较得出广义极值分布连续序列最佳经验概率公式,下面将用2个试验来检验该公式的描述能力和预见能力。针对广义极值分布,在现有的经验频率公式中选择Hazen公式、中值(Median)公式、Weilbull公式、Gringorten公式(只适用于极值Ⅰ型分布,k=0)、Cunnane公式(替代Gringorten公式用于极值Ⅱ、Ⅲ型分布)、Arnell公式、In-na公式和GEVAC公式,通过统计试验方法评价GEVQG与以上经验频率公式优劣性。 2.1 试验1[1,20] (20) 然后,计算出j个经验频率公式[2-3,8-12,20]的P(i),j值,根据下式计算X(i),j: X(i),j=F-1(P(i),j),i=1,2,…,N。 (21) 式中:X(i),j为采用j公式计算的第i阶次序统计量,F-1代表广义极值分布的逆函数,i、j分别代表样本次序和所采用的公式。 (22) (23) 表1列出了样本容量分别为30,50,70时不同经验频率公式在极值Ⅰ型(k=0,均值EX=100,变差系数Cv=0.5,Cs=1.139)、Ⅱ型(k=-0.2,均值EX=100,变差系数Cv=0.5,Cs=3.535)和Ⅲ型(k=0.05,均值EX=100,变差系数Cv=0.5,Cs=0.868)分布时的平均绝对偏差(AD)和均方根误差(RMSE)的计算结果。综合来看,GEVQG公式误差较小,In-na公式在Cs值较小时误差较小,GEVAC公式和Cunnane公式的误差值比较接近,中值(Median)公式和Hazen公式有较大偏差,Weibull公式和Arnell公式的平均绝对偏差和均方根误差均较大(表1)。 表 1 不同经验频率公式平均绝对偏差(AD)和均方根误差(RMSE)的比较 2.2 试验2[1,21] (24) 图2为k=0.1,k=-0.1,k=0时广义极值分布的重现期与相对误差的关系。从图2可以看出,k=0.1和k=-0.1时,Arnell公式和Weibull公式相对误差偏大;k=0时,Weibull公式和中值公式相对误差也较大;In-na公式在部分重现期表现良好,部分重现期相对误差较大;Cunnane公式、Gringorten公式和GEVAC公式的相对误差较小,且三者的相对误差值也很接近;GEVQG公式在分位数估计中表现最为良好。整体上来看,重现期的增大使得各个经验频率公式的相对误差均随之增大。 选择陕西省陕北地区12个水文测站(神木(二)、赵石窑、绥德、交口河、杏河、枣园、吴旗、刘家河、安塞、黄陵、张村驿和志丹)的年最大洪峰流量系列,在资料审查的基础上,采用兼具广泛性和良好统计特性的GEVQG公式、GEVAC公式和Cunnane公式进行洪水频率分析。 利用编制的MATLAB程序对研究区12个水文测站的年最大洪峰流量系列进行频率计算,获得3种经验公式下的点据分布,并与理论频率进行相关关系比较,其中以代表性水文测站黄陵站和刘家河站为例的计算结果见图3。从图3可以看出,经验点数据基本均聚集在45°线附近,由此证明理论分布和样本系列的拟合效果较为良好,即选择的广义极值分布理论与该地区的适合程度较为良好。 图 2 不同形状参数(k)下广义极值分布的重现期与相对误差的关系 △.GEVAC公式 GEVAC formula;*.Cunnane公式 Cunnane formula;○.GEVQG公式 GEVQG formula 图 3 陕北地区2个水文测站年最大洪峰流量经验频率和理论频率的相关关系 Fig.3 Relationship between empirical and theoretical frequencies for annual maximum flood peak flow series at two stations in Northern Shaanxi 采用离差平方和最小准则法(OLS)和相对离差平方和最小准则法(WLS)进行拟合效果的定量评价分析,表2中列出了不同评价方法和不同重现期(50年一遇、100年一遇和200年一遇)下拟合效果最优的经验概率公式。从表2可以看出,拟合效果的评价标准不同,得到的结论也不尽相同。总体上而言,GEVQG公式和Cunnane公式对于大多数测站的拟合效果较为良好。选择代表性水文测站黄陵站和刘家河站为例绘制频率曲线图,结果如图4所示。由图4可以看出,经验点据和理论频率曲线的拟合效果良好,其中曲线中部和尾部的拟合程度最好,可以较好地兼顾曲线首部。 表 2 不同评价方法和重现期下陕北各水文测站拟合效果最优时对应的经验概率公式 ◇.GEVAC公式 GEVAC formula;○.GEVGQ公式 GEVGQ formula;×.Cunnane公式 Cunnane formula 图 4 不同公式拟合陕北地区2个水文测站年最大洪峰流量频率曲线的比较 Fig.4 Comparison of frequency curves for annual maximum flood peak flow series at two stations in Northern Shaanxi with different formulas 1)Goel和De[12]推荐的GEVAC公式基于对称分布的通式进行推导,本研究应用的通式从理论上更适合广义极值分布。 Arnell公式[10]未考虑样本数据的性质,变量之间未形成一个准确的联系,只罗列出了部分Cs、N、m的值,在实际应用中十分不便,而且在Arnell所列的表格中会出现参数α=β的情况,显然这不符合实际。在统计试验中,Arnell公式的偏差很大,因此不建议使用。In-na公式[11]在Cs总体较小时展现出较为良好的统计特性,但在Cs总体较大时会产生较大的偏差,该公式推导时假定的是一组降序排列的数值,所以In-na公式很难应用到水文频率分析中。Weibull公式[3]与总体分布无关,在我国得到了较为广泛的应用,但从统计试验可以看出,Weibull公式误差较大,不宜继续使用。中值公式[20]与总体分布无关,使用简便,一般情况下实测资料被认为是随机独立的,但是中值公式头尾2项的频率间隔与样本中间部分不同,不符合样本各项为等可能独立事件的基本假定,而且在统计试验中,其抽样误差也较大。Hazen公式[2]是纯经验公式,理论基础薄弱,其重现期T=n/(1-0.5)=2n,即n年观测资料中最大项的重现期为2n,也就是说如果要得到100年一遇的结果,只要50年的资料就可以,显然计算结果偏于不安全。Gringortern公式[8]只适用于极值Ⅰ型分布,在统计试验中可以看出,其无偏性和有效性都较优。Cunnane公式[9]和GEVQG公式表现都较好,且统计特性接近,只是GEVQG公式与偏态系数有关,需初定统计参数。 2)对研究区陕北神木(二)、赵石窑、绥德、交口河、杏河、枣园、吴旗、刘家河、安塞、黄陵、张村驿和志丹等12个水文测站洪水频率的实例分析研究表明,采用广义极值分布作为该地区的频率分布曲线合理可行。 3)在实际应用中,推荐将GEVQG公式和Cunnane公式作为广义极值分布的最佳经验概率公式。 [1]郭生练,叶守泽.论水文计算中的经验频率公式 [J].武汉水利电力学院学报,1992(2):38-45. Guo S L,Ye S Z.Another look at plotting position formulae in hydrology [J].Journal of Wuhan University of Hydraulic and Electric Engineering,1992(2):38-45. [2]Hazen A.Storage to be provided in impounding reservoirs for municipal water supply [J].Transactions of the American Society of Civil Engineers,1914,77(1):15-39. [3]Weibull W.A statistical theory of the strength of materials [M].Stockholm:Generalstabens Litografiska Anstals Forlag,1939. [4]Kimball B F.Assignment of frequencies to a completely ordered set of sample data [J].Transactions American Geophysical Union,1946,27(6):843-846. [5]Harter H L.Another look at plotting positions [J].Communications in Statistics-Theory and Methods,1984,13(13):1613-1633. [6]Johnson L G.The median ranks of sample values in their population with an application to certain fatigue studies [J].Bulletin of the American Mathematical Society,1950,56(3):247. [7]Blom G.Statistical estimates and transformed beta-variables [M].New York:Wiley,1958. [8]Gringorten I I.A plotting rule for extreme probability paper [J].Journal of Geophysical Research,1963,68(3):813-814. [9]Cunnane C.Unbiased plotting positions:a review [J].Journal of Hydrology,1978,37(3):205-222. [10]Arnell N W,Beran M,Hosking J R M.Unbiased plotting positions for the general extreme value distribution [J].Journal of Hydrology,1986,86:59-69. [11]In-na N,Nguyen V.An unbiased plotting position formula for the general extreme value distribution [J].Journal of Hydrology,1989,106(89):193-209. [12]Goel N K,De M.Development of unbiased plotting position formula for general extreme value distributions [J].Stochastic Hydrology & Hydraulics,1993,7(1):1-13. [13]De M.A new unbiased plotting position formula for Gumbel distribution [J].Stochastic Environmental Research Risk Assessment,2000,14(1):1-7. [14]Kim S,Shin H,Joo K,et al.Development of plotting position for the general extreme value distribution [J].Journal of Hydrology,2012,475(12):259-269. [15]郭生练.考虑历史洪水资料的频率计算方法 [J].武汉水利电力学院学报,1988(1):15-21. Guo S L.Flood frequency analysis with historic information [J].Journal of Wuhan University of Hydraulic and Electric Engineering,1988(1):15-21. [16]陈兴旺.广义极值分布理论在重现期计算的应用 [J].气象与减灾研究,2008,31(4):52-54. Chen X W.Application of generalized extreme value distribution theory in calculating return periods [J].Journal of Meteorology and Disaster Reduction Research,2008,31(4):52-54. [17]原秀红.基于部分概率权重矩的洪水频率分布参数估计方法研究 [D].陕西杨凌:西北农林科技大学,2014. Yuan X H.Partial probability weighted moments for estimating distribution parameters in flood frequency analysis [D].Yangling,Shaanxi:Northwest A&F University,2014. [18]Jenkinson A F.The frequency distribution of the annual maximum (or minimum) values of meteorological elements [J].Quarterly Journal of the Royal Meteorological Society,1955,81(348):158-171. [19]陈元芳,黄振平.水文统计学 [M].北京:中国水利水电出版社,2011. Chen Y F,Huang Z P.Hydrologic statistics [M].Beijing:China Waterpower Press,2011. [20]Benard A,Bos-Levenbach E C.The plotting of observations on probability paper [J].Statistica Rijswijk,1953:163-173. [21]Guo S L.A discussion on unbiased plotting positions for the general extreme value distribution [J].Journal of Hydrology,1990,121(90):33-44. Plotting position formula for general extreme value distribution QI Zhexian1,2,SONG Songbai1 (1 College of Water Resources and Architectural Engineering,Northwest A&F University,Yangling,Shaanxi 712100,China;2CollegeofCivilEngineeringandArchitecture,ZhejiangUniversity,Hangzhou,Zhejiang310058,China) 【Objective】 This study developed the unbiased plotting position formula for general extreme value (GEV) distribution.【Method】 Based on the theory of order statistics,this paper developed an unbiased plotting position formula for the GEV distribution.The statistical testing was used to compare the developed formula and other existing formulas.At last,the parameters of annual maximum floods peak flow series of twelve stations in Northern Shaanxi were estimated.【Result】 This paper developed a practical and convenient plotting position formula for the GEV distribution.The case study and statistical testing showed that the developed formula and Cunnane formula had small error and bias as well as good fitness in the study area.【Conclusion】 The developed formula and Cunnane formula can be used as better methods for the GEV distribution,which provides new choice for empirical probability calculation in hydrology engineering. unbiased plotting position formula;general extreme value distribution;flood frequency analysis;order statistics;Northern Shaanxi 时间:2016-10-20 16:37 10.13207/j.cnki.jnwafu.2016.12.030 2015-07-10 国家自然科学基金项目(51479171,51179160,71273081);高等学校博士点基金项目(20110204110017) 齐哲娴(1993-),女,河北唐山人,在读博士,主要从事市政工程研究。E-mail:qzx@zju.edu.cn 宋松柏(1965-),男,陕西永寿人,教授,博士,博士生导师,主要从事水文与水资源研究。 E-mail:ssb6533@nwsuaf.edu.cn P333.9 A 1671-9387(2016)12-0219-07 网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20161020.1637.060.html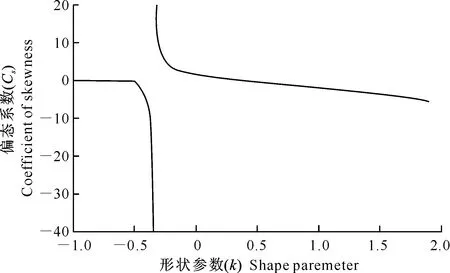
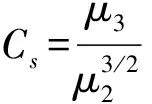
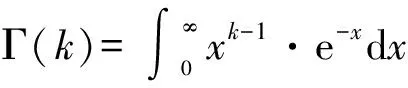

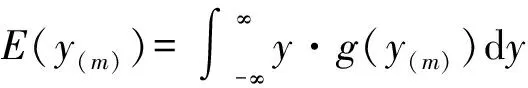
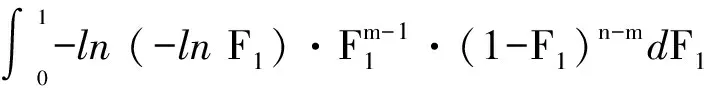
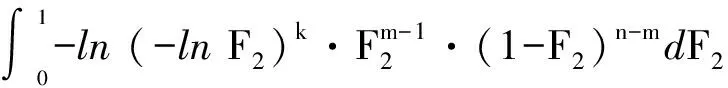
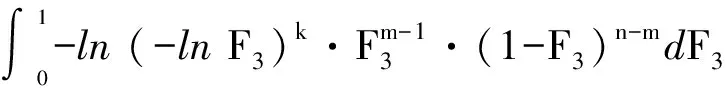
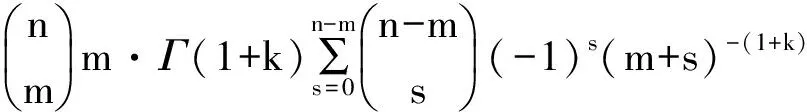
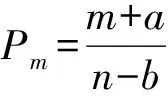
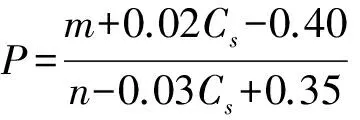
2 统计试验研究
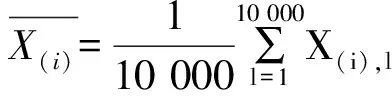
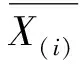
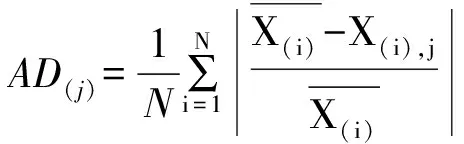
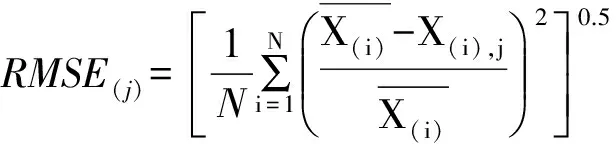
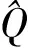
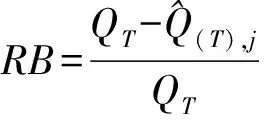
3 实例应用
4 结 论

