级联单模光纤中初始啁啾对高阶孤子脉冲压缩的影响

徐永钊， 张 耿， 叶 海， 刘敏霞

(东莞理工学院 电子工程学院， 广东 东莞 523808)



级联单模光纤中初始啁啾对高阶孤子脉冲压缩的影响

徐永钊， 张 耿， 叶 海， 刘敏霞*

(东莞理工学院 电子工程学院， 广东 东莞 523808)

采用两段级联单模光纤对高阶孤子脉冲进行压缩。两段光纤具有不同的反常色散值，当高阶孤子脉冲在第一段光纤中获得最大程度压缩时，通过转换色散值不同的光纤，使压缩脉冲继续以高阶孤子的形式在第二段光纤中再次被压缩。每段光纤的长度都进行了优化，使得脉冲在每段光纤中都获得最大程度的压缩。基于非线性薛定谔方程，数值研究了初始啁啾对高阶孤子脉冲压缩的影响。研究结果表明，初始啁啾对高阶孤子脉冲的压缩有重要影响。与无初始啁啾时的情形相比，正的初始啁啾能增强每段光纤中脉冲的压缩效果，降低压缩脉冲的基座能量，而负初始啁啾的影响则相反。随着初始啁啾参量Cp的增大，脉冲在每段光纤中的压缩因子均增加，而基座能量、最优光纤长度均减小。

非线性光学； 光脉冲压缩； 光孤子； 啁啾

1 引 言

超短光脉冲在高速光通信、超快光子学、非线性物理以及生物医学等众多领域有重要的应用，脉冲压缩技术的研究一直受到人们广泛的关注[1-7]。利用光纤压缩光脉冲是获得超短光脉冲的主要手段之一，常用的方案有两种：绝热孤子压缩和高阶孤子压缩[8]。绝热孤子压缩技术通常使用色散渐减光纤作为压缩光纤，可以获得基座能量很低的压缩脉冲[9]，但是这种压缩方法需要较长的光纤长度。另外，由于色散渐减光纤色散渐减率的限制，脉冲最大压缩因子的典型值限制在20左右[10]。而利用高阶孤子压缩技术可以获得很高的脉冲压缩因子，但压缩过程中有很多能量转移到基座中，导致压缩脉冲具有宽且高的基座[11]。为了避免这两种压缩技术的显著缺点，Li等[12-13]提出了一种基于级联单模光纤的高阶孤子脉冲压缩技术。他们的方案采用两段或三段具有不同色散的单模光纤级联在一起，对高阶孤子脉冲进行压缩。每段光纤的长度都进行了优化，以使脉冲在每段光纤内都获得最大程度的压缩。研究结果显示，每段光纤的最优长度都小于半个孤子周期，脉冲经过两个或三个阶段的级联压缩，可以获得很高程度的压缩，且基座相对较小。例如，两个阶段的三阶孤子压缩可以获得70.8的压缩因子，基座能量仅为44.8%；三个阶段的三阶孤子压缩则可以获得高达599.7的压缩因子，而基座能量也仅为58.8%。基于级联单模光纤的高阶孤子脉冲压缩技术优于常规的绝热孤子压缩和高阶孤子压缩技术，但是，Li等的研究仅考虑了对无啁啾高阶孤子脉冲压缩的情形。据我们所知，脉冲的初始啁啾对级联高阶孤子脉冲压缩的影响目前还没有这方面的研究报道。众所周知，实际的激光器输出的脉冲经常具有啁啾，作为脉冲的一个重要参量，研究啁啾对脉冲压缩效应的影响具有现实意义。

本文通过数值求解非线性薛定谔方程，研究了初始啁啾对级联单模光纤中高阶孤子脉冲压缩的影响。结果发现，初始啁啾对级联单模光纤中高阶孤子脉冲的压缩有重要影响。

2 理论模型

光脉冲在单模光纤中的传输采用非线性薛定谔方程描述，表示如下[14]：

(1)

其中A为光场振幅，z为传输距离，α为光纤损耗系数，τ为以群速度为移动参考系的时间参量，βm为在中心频率ω0处m阶色散系数，γ为光纤的非线性系数。方程左边第二项为损耗，第三项为色散效应；方程右边第一项为自相位调制(SPM)，后面两项为高阶非线性效应项，分别为自变陡和脉冲内拉曼散射。

假设初始脉冲为双曲正割脉冲，脉冲的光场表达为：

(2)

其中，P0是脉冲的峰值功率；T0为脉冲1/e强度处的半宽度，对于双曲正割脉冲，T0与脉冲的半高全宽(TFWHM)的关系为TFWHM≈1.763T0；Cp为脉冲的初始线性啁啾参量。

本文研究高阶孤子脉冲在单模光纤中的压缩，脉冲的孤子阶数N定义为：

(3)

其中LD和LNL分别为色散长度和非线性长度。对于高阶孤子脉冲，N>1。高阶孤子脉冲在光纤中传输时，其波形会发生周期性的演化，孤子周期为：

(4)

基于级联光纤的高阶孤子脉冲压缩技术的原理是当高阶孤子在一段光纤中获得最大程度的压缩时，立刻输入到下一段光纤，通过转换光纤的色散，使输入脉冲在接下来的光纤中重新作为高阶孤子继续被压缩。在级联压缩的过程中，每段光纤都选取最优的光纤长度和适当的色散值，使脉冲作为高阶孤子在每个阶段都达到最大程度的压缩。经过两段或三段级联光纤，即通过两个或三个阶段的级联压缩，脉冲最终可以获得很高的压缩因子。为了衡量脉冲压缩后的质量，引入压缩因子FC和基座能量(%)两个参量进行描述，其中压缩因子FC定义为初始脉冲的宽度与压缩后脉冲的宽度之比：

(5)

压缩脉冲的基座能量定义为：

(6)

其中，Etotal是压缩脉冲的总能量，Esech是理想双曲正割脉冲的能量，该双曲正割脉冲具有与压缩脉冲相同的宽度(TFWHM)和峰值强度。认为压缩脉冲有基座，双曲正割脉冲无基座，则两者能量之差相对于压缩脉冲的总能量即为压缩脉冲的基座能量，代表基座能量所占压缩脉冲总能量的百分比。

3 结果与讨论

本文考虑基于两段级联光纤的高阶孤子压缩的情形。设第一段光纤初始输入脉冲的孤子阶数为N1，当脉冲在第一段光纤中压缩到最大程度时从光纤中输出，并输入到第二段光纤中。设第二段光纤输入脉冲的孤子阶数为N2。假设N1=N2=N，且两段光纤的非线性系数相同(γ=2.5 W/km)，其他参量的取值分别为：初始脉冲的宽度TFWHM=30 ps，第一段光纤的二阶色散系数β21=-20 ps2/km(反常色散)。在数值计算中，忽略光纤衰减的影响。另外，为便于与文献[12]的结果进行比较，我们参考其做法，忽略了高阶色散和高阶非线性效应的影响。实际上，对于T0>5 ps的脉冲，高阶色散和高阶非线性效应对脉冲传输的影响很小。

图1 无初始啁啾的三阶孤子(N=3)脉冲的峰值功率在一个孤子周期内的演化图。(a)第一段光纤中一个孤子周期z01内的演化图；(b)第二段光纤中一个孤子周期z02内的演化图。

Fig.1 Peak power evolution of the third order soliton (N=3) pulse within one soliton period. (a) Peak power evolution in the first fiber within one soliton periodz01. (b) Peak power evolution in the second fiber within one soliton periodz02.

首先考虑无初始啁啾的三阶孤子(N=3)脉冲在光纤中压缩的情形。图1(a)所示为第一段光纤内，脉冲的峰值功率在一个孤子周期z01内的演化图。图中虚线所标记的位置为脉冲峰值功率达到最大值时的相对位置L1/z01，在该位置脉冲获得最大程度的压缩，相应的光纤长度L1为第一段光纤的最优长度。脉冲在L1处输出后，随即作为第二段光纤的输入脉冲。若第二段光纤的二阶色散系数β22取值为-1.769 ps2/km时，可使得输入脉冲的孤子阶数仍然为N=3。图1(b)所示为第二段光纤内，脉冲的峰值功率在一个孤子周期z02内的演化图。可以看到，在一个孤子周期内，脉冲的峰值功率在两段光纤中演化的情形极为相似，而且L1/z01≈L2/z02。与图1(a)类似，脉冲在相对位置L2/z02处获得最大程度的压缩，第二段

光纤的最优长度为L2。表1给出了无初始啁啾的三阶孤子压缩时的光纤设计。脉冲经过第一段光纤的压缩，获得的压缩因子为8.4，基座能量为26.0%(基座能量所占脉冲总能量的百分比)；经过第二段光纤的压缩，最终获得的压缩因子为70.8，基座能量为44.8%。

表1 无初始啁啾(Cp=0)的三阶孤子(N=3)脉冲压缩时的光纤设计

Tab.1 Fiber design in pulse compression forN=3 andCp=0

β2i/(ps2·km-1)Li/kmLi/Z0i第一段光纤-205.3910.237第二段光纤-1.7690.8650.235

接下来，我们改变脉冲的初始啁啾参量Cp，研究初始啁啾对三阶孤子脉冲压缩的影响。图2(a)和(b)分别给出了脉冲经过第一段光纤和第二段光纤压缩后，压缩因子和基座能量随初始啁啾参量Cp的变化曲线。由图可见，随着啁啾参量Cp的增大，压缩因子单调增加，而基座能量则单调减小。在两段光纤中，压缩因子和基座能量随初始啁啾参量Cp的变化规律相同。与无初始啁啾(Cp=0)时的情形相比，可以发现，正初始啁啾(Cp>0)可以增强脉冲的压缩效果，减小压缩脉冲的基座能量。当正啁啾较大时，这种效果非常显著。例如，与Cp=0时的结果相比，当Cp=4时，脉冲经过第一段光纤的压缩，压缩因子由8.4增加到12.0，而基座能量由26.0%减少到仅9.0%；经过第二段光纤的压缩，压缩因子由70.8增加到102.0，而基座能量则由44.8%减少到31.8%。相反，负初始啁啾(Cp<0)会使脉冲的压缩效果减弱，基座能量增加。负初始啁啾值越大(负初始啁啾参量的绝对值Cp越大)，脉冲压缩的质量越差。

为比较压缩的效果，图3(a)和(b)分别给出了三阶孤子在第一段和第二段光纤中，当Cp=0和Cp=4时，脉冲压缩程度最大时的波形。通过图3中脉冲波形的对比，可以清晰地看出正初始啁啾对脉冲压缩效果的改善。

图2 初始啁啾对压缩因子和基座能量的影响。(a)脉冲在第一段光纤的压缩因子和基座能量随初始啁啾参量Cp的变化曲线；(b)脉冲在第二段光纤的压缩因子和基座能量随初始啁啾参量Cp的变化曲线。

Fig.2 Effect of initial chirp on compression factor and pedestal energy. (a) Calculated compression factor and pedestal energy as a function ofCpin the first fiber. (b) Calculated compression factor and pedestal energy as a function ofCpin the second fiber.

图3 当Cp=0和Cp=4时，三阶孤子脉冲在第一段和第二段光纤中压缩程度最大时的波形。(a)脉冲在第一段光纤中压缩程度最大时的波形；(b)脉冲在第二段光纤中压缩程度最大时的波形。

Fig.3 Pulse shapes where compression is maximized in both the first and second fibers of the third-order soliton whenCp=0 andCp=4. (a) Pulse shapes where compression is maximized in the first fiber. (b) Pulse shapes where compression is maximized in the second fiber.

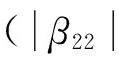
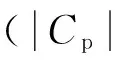
图4 第二段光纤的色散值与第一段光纤的色散值的比值β22/β21随初始啁啾参量Cp的变化曲线

Fig.4β22/β21as a function ofCp

图5 第一段光纤(a)和第二段光纤(b)的最优光纤长度和最优光纤长度与孤子周期的比值随初始啁啾参量Cp的变化曲线

Fig.5 Optimal length and the ratio of optimal length to soliton period of the first fiber (a) and the second fiber (b) as a function ofCp

为便于比较，图5中同时也给出了两段光纤的最优长度与孤子周期的比值Li/z0i(i=1,2)随初始啁啾参量Cp的变化曲线。在第一段光纤中，L1/z01和L1随啁啾参量Cp的变化趋势相同；但在第二段光纤中，L2/z02基本保持不变，与初始啁啾参量Cp无关。L2/z02仅与输入第二段光纤的孤子阶数N有关。

保持初始脉冲的孤子阶数不变，我们计算了不同宽度脉冲的压缩效果。结果表明，在不考虑损耗、高阶色散和高阶非线性效应的情况下，当初始啁啾相同时，对于不同宽度的初始脉冲，其压缩因子、基座能量的占比以及两段光纤最优长度与孤子周期的比值Li/z0i均保持不变。

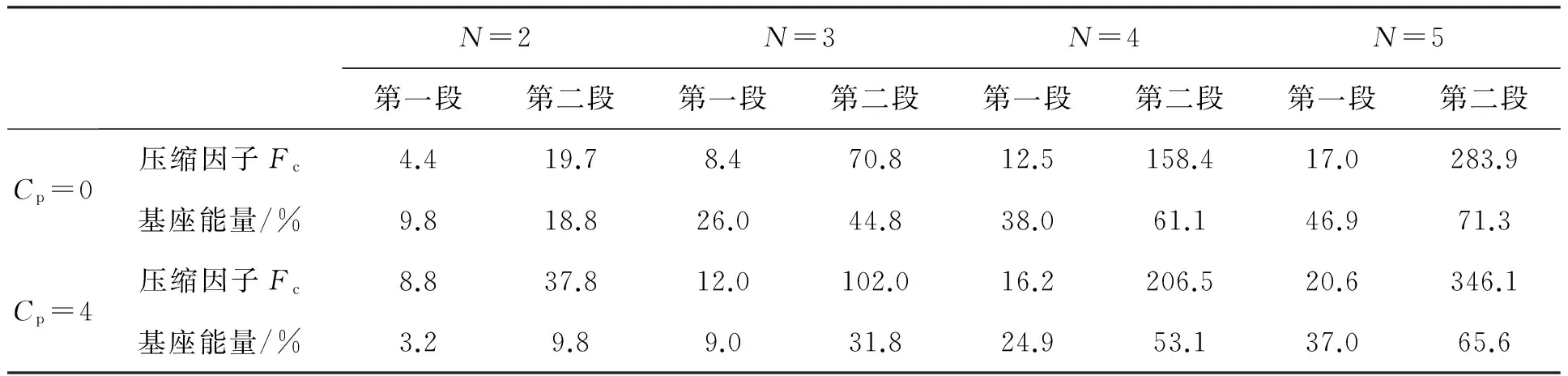
表2 初始啁啾参量Cp=0和Cp=4时，不同孤子阶数的脉冲在两段级联光纤中的压缩因子和基座能量

我们同时也研究了其他阶数的高阶孤子脉冲压缩的情形。结果发现，初始啁啾对不同阶数的高阶孤子的影响有相同的规律。表2给出了初始啁啾参量Cp=0和Cp=4时，不同孤子阶数的脉冲在两段级联光纤中的压缩因子和基座能量的对比，其中初始啁啾参量Cp=0时的结果即文献[12]的计算结果。表2的结果显示，与无初始啁啾时的情形相比，当Cp=4时，不同N值的压缩因子都有显著的提高，而基座能量都明显降低。另外，N值越小，初始啁啾的影响越显著。例如，当Cp=4时，对于二阶孤子(N=2)，与无初始啁啾时的情况相比，经过第一级压缩后，压缩因子增大了一倍，而基座能量减少67%；经过第二级压缩后，压缩因子也接近增大一倍，而基座能量减少48%。随着孤子阶数的增加，压缩因子的增幅减小，基座能量下降的幅度也减小。

表3给出了Cp=4时，不同N值的高阶孤子的两段级联光纤的设计参数。结果显示，在相同初始啁啾的情况下，随着N的增加，两段光纤色散值的比值β22/β21减小。另外，随N值的增加，L1/z01和L2/z02同时减小。这表明脉冲的孤子阶数越高，在一个孤子周期内发生最大程度压缩的相对距离越短。例如，当N=2时，第一段光纤和第二段光纤分别在L1=0.146z01处和L2=0.475z02处发生最大程度的压缩；当N=5时，第一段光纤和第二段光纤分别在L1=0.0735z01处和L2=0.109z02处发生最大程度的压缩。当Cp=4时，对于不同的N值，两段光纤的最优长度L1和L2均小于半个孤子周期。

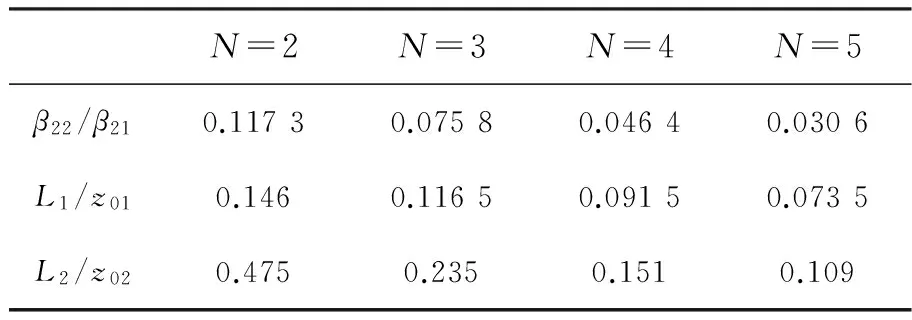
表3 Cp=4时，两段级联光纤的设计

4 结 论

本文数值研究了初始啁啾对两段级联单模光纤中高阶孤子脉冲压缩的影响。研究结果表明，与无初始啁啾时的情形相比，正的初始啁啾能增强每段光纤中脉冲的压缩效果，降低压缩脉冲的基座能量，而负初始啁啾的影响则相反。随着初始啁啾参量Cp的增大，脉冲在每段光纤中的压缩因子均增加，而基座能量均减小。当正初始啁啾较大时，与无初始啁啾的情形相比，脉冲压缩的质量可以获得十分显著的改善。另外，随着初始啁啾参量Cp的增大，两段光纤的最优长度以及第一段光纤的最优长度与孤子周期的比值L1/z01均减小，而第二段光纤的最优长度与孤子周期的比值L2/z02则保持不变，与初始啁啾无关。对于不同阶数的高阶孤子，初始啁啾对脉冲压缩的影响也不同。当脉冲具有相同正初始啁啾时，随着孤子阶数的增加，与无初始啁啾的情形相比，压缩因子的增幅减小，基座能量下降的幅度也减小。

[1] 曹文华,徐平,刘颂豪. 马赫-曾德尔型色散渐减光纤干涉仪的孤子效应脉冲压缩研究 [J]. 光学学报, 2011, 31(4):419001-1-8. CAO W H, XU P, LIU S H. Soliton-effect pulse compression in a dispersion-decreasing fiber-based Mach-Zehnder interferometer [J].ActaOpt.Sinica, 2011, 31(4):419001-1-8. (in Chinese)

[2] 李博,娄淑琴,谭中伟,等. 两种基于交叉相位调制的光脉冲压缩方案 [J]. 物理学报, 2012, 61(19):194203-1-7. LI B, LOU S Q, TAN Z W,etal.. Two kinds of optical pulse compression approaches based on cross phase modulation [J].ActaPhys.Sinica, 2012, 61(19):194203-1-7. (in Chinese)

[3] WANG D, LENG Y X, XU Z Z. Optical pulse compression of ultrashort laser pulses in a multi-hollow-core fiber [J].Opt.Commun., 2012, 285(9):2418-2421.

[4] VORONIN A A, MIKHAILOVA J M, GORJAN M,etal.. Pulse compression to sub-cycle field waveforms with split-dispersion cascaded hollow fibers [J].Opt.Lett., 2013, 38(21):4354-4357.

[5] LEFORT C, KALASHYAN M, DUCOURTHIAL G,etal.. Sub-30-fs pulse compression and pulse shaping at the output of a 2-m-long optical fiber in the near-infrared range [J].J.Opt.Soc.Am. B, 2014, 31(10):2317-2324.

[6] BANANEJ A, AGHAEE A K, MADJABADI A,etal.. Adjustable enhancement of higher order soliton effect pulse compression by using optimized active dispersion decreased nonlinear fiber loop mirror [J].Optik-Int.J.LightElectronOpt., 2014, 125(19):5476-5479.

[7] RUBENCHIK A M, CHEKHOVSKOY I S, FEDORUK M P,etal.. Nonlinear pulse combining and pulse compression in multi-core fibers [J].Opt.Lett., 2015, 40(5):721-724.

[8] AGRAWAL G P.ApplicationofNonlinearFiberOptics[M]. 2nd ed. New York: Academic Press, 2008.

[9] MOSTOFI A, HATAMI-HANZA H, CHU P L. Optimum dispersion profile for compression of fundamental solitons in dispersion decreasing fibers [J].IEEEJ.Quant.Electron., 1997, 33(4):620-628.

[10] PELUSI M D, LIU H F. Higher order soliton pulse compression in dispersion-decreasing optical fibers [J].IEEEJ.Quant.Electron., 1997, 33(8):1430-1439.

[11] CHAN K, LIU H F. Short pulse generation by higher order soliton-effect compression: effects of optical fiber characteristics [J].IEEEJ.Quant.Electron., 1996, 31(12):2226-2235.

[12] LI Q, KUTZ J N, WAI P K A. Cascaded higher-order soliton for non-adiabatic pulse compression [J].J.Opt.Soc.Am. B, 2010, 27(11):2180-2189.

[13] LI Q, KUTZ J N, WAI P K A. High-degree pulse compression and high-coherence supercontinuum generation in a convex dispersion profile [J].Opt.Commun., 2013, 301-302:29-33.

[14] AGRAWAL G P.NonlinearFiberOptics[M]. San Diego: Academic Press, 2007.

徐永钊(1972-)，男，广东广州人，博士，副教授，2007年于北京邮电大学获得博士学位，主要从事光纤通信技术、非线性光纤光学的研究。

E-mail： yongzhaoxu@126.com刘敏霞(1979-)，女，河北石家庄人，博士，副教授，2007年于北京大学获得博士学位，主要从事光电材料、非线性光学的研究。

E-mail： liumxdgut@qq.com

Effect of Initial Frequency Chirp on Pulse Compression of Higher-order Solitons in Cascaded Single-mode Fibers

XU Yong-zhao， ZHANG Geng， YE Hai， LIU Min-xia*

(SchoolofElectronicEngineering,DongguanUniversityofTechnology,Dongguan523808,China)

We consider the pulse compression of higher-order solitons in two cascaded single-mode fibers. The two single-mode fibers have different anomalous dispersion value. When the higher-order soliton pulse achieves maximal compression in the first fiber, by switching the fiber with different dispersion, the pulse is compressed again as a new higher-order soliton in the second fiber. Each fiber length is optimized in order to achieve maximal compression inside each fiber segment. Based on the generalized nonlinear Schrödinger equation, we numerically study the effect of initial frequency chirp on pulse compression of higher-order solitons. Our numerical results show that initial frequency chirp has significant influence on higher-order solitons pulse compression. In comparison with the case of without initial chirp, a positive chirp can enhance the pulse compression and can reduce the pedestal energy in each fiber segment, while a negative chirp does the opposite. In each fiber segment, as the chirp parameterCpincreases, the compression factor increases, while pedestal energy and optimal fiber length decrease.

nonlinear optics; optical pulse compression； optical solitons； chirp

1000-7032(2016)11-1360-07

2016-05-07；

2016-06-20

国家自然科学基金(61501118)； 广东省自然科学基金(2014A030310262)资助项目

TN929．11

A

10.3788/fgxb20163711.1360

*CorrespondingAuthor,E-mail:liumxdgut@qq.com