基于大数据的配电网络复合攻击预测方法研究

王国欢，李敏，陶振文

（1.国网江西省电力公司信息通信分公司，江西南昌 330007；2.国网江西省电力公司，江西南昌 330007）

基于大数据的配电网络复合攻击预测方法研究

王国欢1，李敏1，陶振文2

（1.国网江西省电力公司信息通信分公司，江西南昌 330007；2.国网江西省电力公司，江西南昌 330007）

当前配电网络复合攻击环境较为复杂，有很大的不确定性，当前复合攻击预测方法收敛性较低，很难准确预测出攻击背景，导致预测结果不可靠。提出一种新的基于大数据的配电网络复合攻击预测方法，对配电网络中的报警数据进行预处理，以提高效率。在大数据分析的基础上，将隐马尔科夫模型应用于配电网络复合攻击预测中，要求配电网络依据得到的报警信息对隐藏的攻击行为进行挖掘。通过攻击行为概率分布、关联规则法得到初始状态矩阵、状态转移矩阵以及观察矩阵，引入粒子群算法对参数进行全局优化。通过隐马尔科夫模型中的Viterbi算法对配电网络复合攻击的攻击意图进行挖掘，预测下一步攻击。实验结果表明，所提方法具有很高的收敛性和预测精度。

大数据；配电网络；复合攻击预测

随着人们生活水平的逐渐提高，电力在人们的生活和工作中起到了越来越关键的作用，人们对配电网络安全性的要求越来越高[1-2]。复合攻击中每个攻击行为之间都在一定程度上有所联系，这些联系主要包括串联、并联和并发，给配电网络的安全性带来了很大的威胁[3-5]。因此，研究配电网络复合攻击预测方法成为亟需解决的问题，能够为预防复合攻击提供重要依据，更好地保证配电网络的安全性[6]。

文献[7]提出一种基于响应事件相关性的复合攻击预测方法，该方法利用复合攻击事件之间的关系对未来一段时间内相同攻击者的攻击行为进行预测。该方法效率高，但因为配电网络攻击的复杂性，通过具体攻击行为获取攻击行为关系是非常困难的；文献[8]提出一种基于攻击树的复合攻击预测方法，通过先验概率与攻击概率对复合攻击进行预测。该方法实现过程简单，但实时性较差；文献[9]提出一种基于攻击意图的复合攻击预测方法，该方法用攻击意图对复合攻击进行描述，通过扩展的有向图体现攻击意图间的逻辑关系，塑造攻击意图模型，实现复合攻击预测，预测效果较好，但需要先验知识；文献[10]提出一种基于系统状态集合的复合攻击预测方法，通过系统状态集合构建复合攻击模型，利用该模型发现攻击行为之间的关系，从而实现复合攻击预测。该方法预测时间少，但精度较低。

针对上述方法的弊端，提出一种新的基于大数据的配电网络复合攻击预测方法，对配电网络中的报警数据进行预处理，以提高效率。在大数据的基础上，将隐马尔科夫模型应用于配电网络复合攻击预测中，实现配电网络复合攻击预测。实验结果表明，所提方法具有很高的收敛性和预测精度。

1 基于大数据的配电网络复合攻击预测方法

现代化配电网络结构复杂、集成度高，容易遭受攻击，对配电网络的安全性提出了更高的要求。随着信息化的深入，配电网络数据库中大数据的存在为预测复合攻击提供了很好的平台。将大数据作为基础，通过隐马尔科夫模型对配电网络复合攻击进行预测。

1.1 配电网络报警数据预处理

配电网络中数据量非常大，以大数据为基础，首先对报警数据进行预处理，以提高效率，详细实现过程描述如下：

假设用SA（Ai，Aj）、Sdes（Ai，Aj）和Sstamp（Ai，Aj）描述报警事件Ai、Aj的名称相似隶属函数、目的IP地址相似隶属函数与事件间隔的相似隶属函数，公式描述如下：

则总相似隶属度函数可通过下式求出：

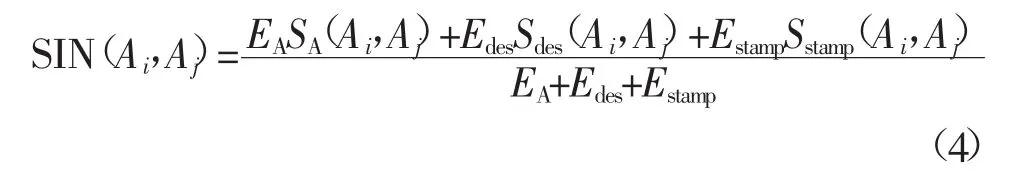
式中：EA、Edes和Estamp分别为配电网络中报警事件的名称、目标IP地址及权重系数，EA+Edes+Estamp=1，本节EA、Edes和Estamp值分别取0.6、0.4、0.3。

假设此刻已经处理了N－1个配电网络中的报警信息，当接收到第N个报警信息时，需比较前N－1个报警信息，以获取N－1个SIN值，则有：

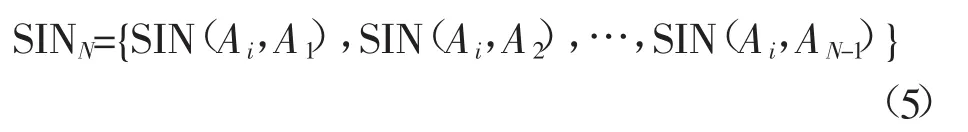
式中：Ai为配电网络已经接收到的报警信息。SINM= max（SINN），如果SINM超过既定阈值，则合并新的报警信息与第m个报警信息；反之，将第m个报警信息看作新的报警信息，从而实现配电网络报警信息的预处理。

1.2 配电网络复合攻击预测的实现

复合式攻击是当前配电网络攻击中的主要形式，在大数据分析的基础上，依据配电网报警数据预处理结果，通过隐马尔科夫模型对配电网络复合攻击进行预测。

在大数据分析的基础上，将隐马尔科夫模型应用于配电网络复合攻击预测中，要求配电网络依据得到的观察值（报警信息），对隐藏的真实状态（攻击行为）进行挖掘，基本思想如下：完成对原始报警信息的预处理后，通过攻击行为概率分布、关联规则法得到初始状态矩阵、状态转移矩阵以及观察矩阵，引入粒子群算法对参数进行全局优化。最后通过隐马尔科夫模型中的Viterbi算法对配电网络复合攻击的攻击意图进行挖掘，同时预测下一步攻击。

1.2.1 隐马尔可夫模型理论

隐马尔可夫模型实质上是统计学习模型，主要由初始状态概率分布矩阵、状态转移概率分布矩阵、观测概率分布矩阵确定，隐马尔可夫模型理论可描述如下：

用Q描述全部可能状态集合，Q={q1，q2，…，qN}；用V描述全部可能观测值集合V={v1，v2，…，vM}；其中N用于描述状态数，M用于描述观测值数，I用于描述长度为T的状态序列，I={i1，i2，…，iT}，O用于描述观测序列，O={o1，o2，…，oT}。

A用于描述状态转移概率分布矩阵。A=[aij]N*N，其中，aij用于描述t时刻处于qi且在t+1时刻转移到qj的概率，可通过下式求出：

B用于描述观测概率分布矩阵。B=[bj（k）]N*M，其中，bj（k）用于描述t时刻处于qj同时产生观测值vk的概率，可通过下式求出：

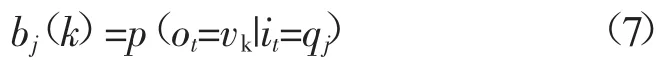
PI用于描述初始状态概率分布矩阵，PI=（PIi），其中PIi用于描述t=1时刻处于qi的概率，公式描述如下：

隐马尔科夫模型取决于PI、A及B，状态序列可通过PI与A确定，观测值序列可通过B确定。所以，隐马尔科夫模型λ可通过三元组λ=（A，B，PI）进行描述。

1.2.2 状态转移矩阵的确定

配电网络中状态之间的相互转换构成状态转移矩阵A，而关联规则主要负责统计配电网络复合攻击数据库中所有攻击之间的联系，该思想可应用于配电网络复合攻击预测中。在复合攻击中任意2个攻击意图intenti、intentj之间的状态转移概率P（intenti，intentj）可通过下式求出：

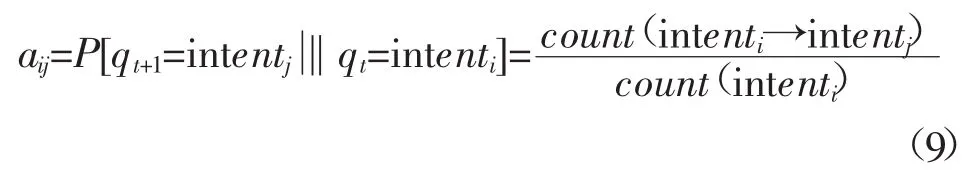
通过上述过程挖掘出配电网络复合攻击意图之间的关联规则，从而求出任意2个攻击意图间的转移概率aij，获取状态转移概率矩阵A。

1.2.3 观察矩阵的确定

因为观察矩阵中不同状态形成观察值的概率不同，所以本节通过统计的方法对观察矩阵进行确定。假设配电网络中共存在n个复合攻击事务集T= {t1，…，tn}，m个攻击意图Q={intent1，…，intentm}。某攻击意图intentj上的报警信息集用Alert={Alert1，…，Alertt}进行描述，第i个攻击事物用ti=（ti[1]，…，ti[f]）进行描述，ti攻击事物中各分量构成攻击意图的集合为intent=（ti[1]，…，ti[f]），攻击者达到攻击意图j后，给出报警信息Alert，其中Alert∈{Alert1，…，Alertt}的概率为：

式中：Sij，Alert={intent|intent∈Sij}为在集合Sij中得到的报警信息Alert的攻击意图集合。通过上式得到的概率值即为bj（k），将其代入式（7）即可确定观察矩阵B。

1.2.4 参数的全局优化

隐马尔科夫模型会使参数收敛于局部极值，导致得到的配电网络复合攻击预测结果不可靠，不一定是最优值，本节通过粒子群算法对隐马尔科夫模型中的参数进行优化。

在粒子群算法中，所有个体均被称作一个粒子，N个粒子将构成一个群体，每个粒子i及其移动速度均是m维向量，分别记作xi（i=1，2，…，N）和vi（i= 1，2，…，N）。用f（x）描述待优化的目标函数，则粒子群优化公式可描述成：

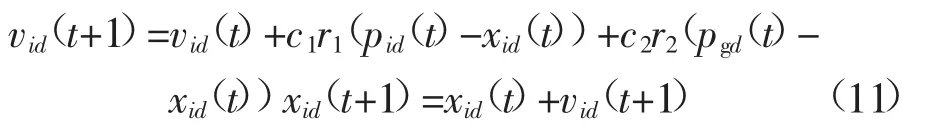
式中：ω为惯性因子；c1、c2为学习因子；r1、r2为加速系数，是[0，1]范围内的随机数；pi（t）（i=1，2，…，N）用于描述第i个粒子在t时刻搜索到的最佳位置，也就是当前极值；pg（t）为整个粒子群搜索到的最佳位置，也就是全局极值。采用粒子群算法对隐马尔科夫模型中的参数进行优化时，每个粒子对应一个隐马尔科夫模型的参数，从而实现参数的全局优化。

1.2.5 复合攻击预测

通过隐马尔科夫模型中的Viterbi算法对配电网络复合攻击的攻击意图进行挖掘，同时预测下一步攻击，下面给出实现过程：

1）通过下式对参数进行初始化处理：

2）通过下式进行迭代计算：

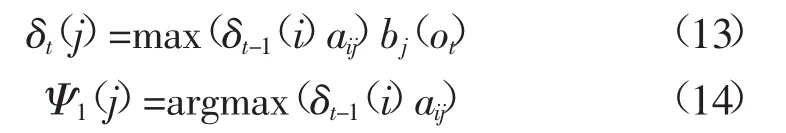
3）当符合下式描述的终止条件时，结束迭代：

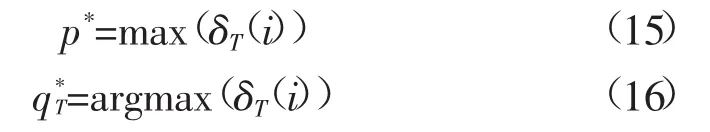
4）通过下式求解最佳攻击路径，对配电网络复合攻击进行预测：

2 实验结果分析

2.1 测试环境

为了验证本方法的有效性，需要进行相关的实验分析。实现将攻击树方法和模糊时间序列方法作为对比进行测试。

首先搭建一个如图1所示的实验配电网络，对该网络进行扫描，采集数据构建配电网络主机表、网络主机连接表等数据表，再按照计划进行攻击。

图1 实验配电网络拓扑图Fig.1 Topology of the experimental distribution network

2.2 收敛速度测试

对本方法、攻击树方法和模糊时间序列方法的收敛性进行测试，收敛速度越快，则预测的攻击路径越准确。图2描述的是本文方法、攻击树方法和模糊时间序列方法的收敛速度比较结果。

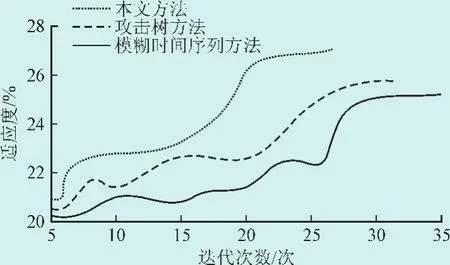
图2 3种方法收敛速度比较结果Fig.2 Comparison of convergence rates of the three methods

分析图2可以看出，本文方法不仅收敛速度明显快于攻击树方法和模糊时间序列方法，而且迭代次数也明显低于其他2种方法，说明通过本文方法得到的攻击路径为最佳路径，以此确定的预测结果可靠性很高。

2.3 复合攻击预测结果

实验将配电网络中的部分DDoS攻击数据集和FTP Bounce攻击数据集作为实验数据集，构建2个攻击场景。

实验首先对配电网络复合攻击场景进行识别，得到的结果用图3进行描述。

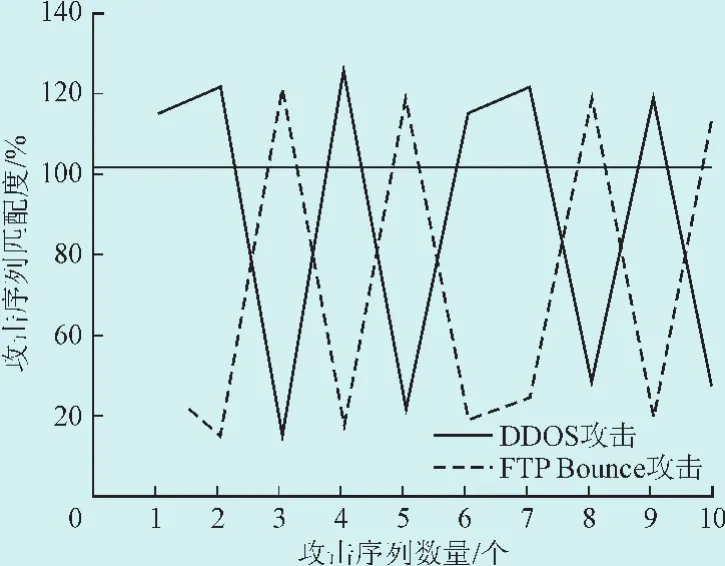
图3 复合攻击场景识别结果Fig.3 Recognition results of composite attack scenarios

分析图3可以看出，在对DDoS攻击场景进行识别时，共存在6个峰值，而对FTP Bounce攻击场景进行识别时共存在4个峰值。说明在10条时间序列中，有6条攻击序列属于DDoS攻击场景，其他4条攻击序列属于FTP Bounce攻击场景。

分别采用本文方法、攻击树方法和模糊时间序列方法对上述识别的配电网络复合攻击进行预测，3种方法的预测准确率如图4所示。

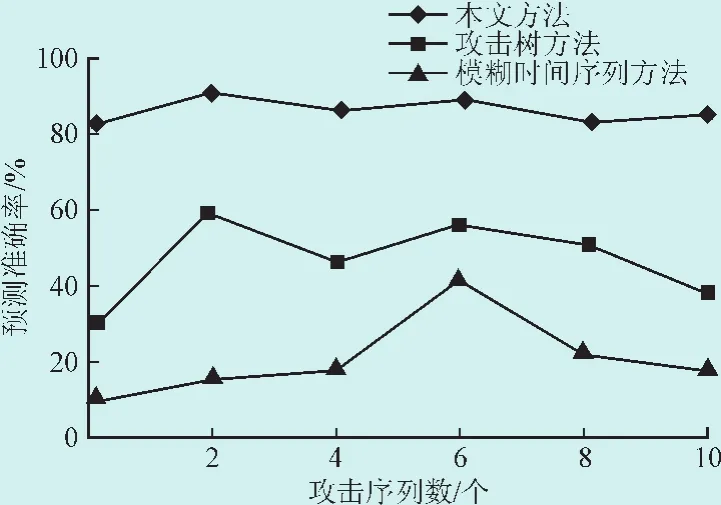
图4 3种方法预测准确率比较结果Fig.4 Comparison of the accuracy results by 3 methods

分析图4可以看出，采用本文方法对配电网络复合攻击进行预测的准确率明显高于攻击树方法和模糊时间序列方法，且一直高于2种方法，说明本文方法的预测精度最高。

3 结论

本文提出一种新的基于大数据的配电网络复合攻击预测方法，对配电网络中的报警数据进行预处理，通过攻击行为概率分布、关联规则法得到初始状态矩阵、状态转移矩阵以及观察矩阵，引入粒子群算法对参数进行全局优化。通过隐马尔科夫模型中的Viterbi算法对配电网络复合攻击的攻击意图进行挖掘，预测下一步攻击。实验结果表明，所提方法具有很高的收敛性和预测精度。

[1]饶尧，邱泽晶，彭旭东.基于层次分析法的电网能效影响因子分析研究[J].节能技术，2014，32（1）:51-54.RAO Yao，QIU Zejing，PENG Xudong.Analysis of grid energy efficiency factors based on analytic hierarchy process[J].Energy Conservation Technology，2014，32（1）: 51-54（in Chinese）.

[2]康忠健，刘睿莹，田爱娜.适用于非同步采样的含DG配电网多端单相故障定位方法研究[J].电网与清洁能源，2015，31（12）:1-6.KANG Zhongjian，LIU Ruiying，TIAN Aina.Fault location in distribution network with DG suitable for nonsynchronous sampling[J].Power System and Clean Energy，2015，31（12）:1-6（in Chinese）.

[3]方健，徐栎，季时宇，等.基于状态矩阵的大型城市配电网可靠性评估研究[J].电网与清洁能源，2015，31（4）: 59-65.FANG Jian，XU Li，JI Shiyu，et al.Study on reliability assessment of large urban distribution network based on the equipment state matrix[J].Power System and Clean Energy，2015，31（4）:59-65（in Chinese）.

[4]张雪峰，龚浩，别士光，等.含分布式电源的配电网网损组合优化[J].科学技术与工程，2014，14（30）:46-50.ZHANG Xuefeng，GONG Hao，BIE Shiguang，et al.Combinatorial optimization of distribution network loss with distribution generaltions[J].Science Technology and Engineering，2014，14（30）:46-50（in Chinese）.

[5]李闫远，刘会家，胡頔，等.基于自动区域模型的含分布式电源配电网可靠性评估[J].陕西电力，2015，43（2）:49-52.LI Yanyuan，LIU Huijia，HU Di，et al.Reliability evaluation of distributed network with DG based on automatic area model[J].Shaanxi Electric Power，2015，43（2）:49-52（in Chinese）.

[6]何健，陈光宇，张杭，等.考虑安全性的含风电场配电网动态无功优化[J].陕西电力，2014，42（9）:48-52.HE Jian，CHEN Guangyu，ZHANG Hang，et al.Dynamic reactive power optimization of distribution system with wind farm considering security[J].Shaanxi Electric Power，2014，42（9）:48-52（in Chinese）.

[7]陈靖，路志英，刘洪，等.基于改进 ANP的配电网综合评估方法及应用[J].电力科学与工程，2015（5）:21-28.CHEN Jing，LU Zhiying，LIU Hong，et al.Research and application of a comprehensive distribution network assessment method based on improved ANP[J].Electric Power Science and Engineering，2015（5）:21-28（in Chinese）.

[8]李平，武建文，张之昊，等.基于双DSP结构的配电网静止同步补偿器设计[J].高压电器，2015（9）:28-33.LI Ping，WU Jianwen，ZHANG Zhihao，et al.Design of the distribution static synchronous compensator based on dual-DSP[J].High Voltage Apparatus，2015（9）:28-33（in Chinese）.

[9]沈琦，陈博.基于大数据处理的ETL框架的研究与设计[J].电子设计工程，2016，24（2）:25-27.SHEN Qi，CHEN Bo.Research and design of ETL framework based on data processing[J].Electronic Design Engineering，2016，24（2）:25-27（in Chinese）.

[10]马业宁.先进节能技术在西石门铁矿配电系统中的应用[J].节能技术，2013，31（4）:95-99.MA Yening.The application of energy saving technology in power distribution system ofXishimen iron mines[J].Energy Conservation Technology，2013，31（4）:95-99（in Chinese）.

（编辑 徐花荣）

Research on the Prediction Method of Composite Attacks of Distribution Network Based on Large Data

WANG Guohuan1，LI Min1，TAO Zhenwen2
（1.Information&Telecommunication Branch of State Grid Jiangxi Electric Power Company，Nanchang 330007，Jiangxi，China；2.Stat Grid Jiangxi Electric Power Company，Nanchang 330007，Jiangxi，China）

At present，the environment of the distribution network composite attack is complicated with a large amount of uncertainty，and the prediction method of the composite attack is of low convergence，thus it is difficult to accurately predict the attack background，resulting in unreliable prediction results.Based on large data，this paper proposes a new prediction method for the composite attack，by which the alarm data can pretreated in the distribution network to improve the efficiency.On the basis of large data analysis，the hidden Markov model（HMM）is applied in the prediction，which requires the distribution network to mine the hidden attack behavior according to the information

.The initial state matrix，state transition matrix and observation matrix are obtained by the probability distribution of the attack behavior and associated rules method，and the parameters are optimized by the particle swarm optimization algorithm.The intention of the composite attack is explored through the Viterbi algorithm of the hidden Markov model to predict the next attack.The experimental results show that the proposed method has high convergence and prediction accuracy.

bigdata；distributionnetwork；composite attack prediction

国家级青年基金面上项目（51677047）。

ProjectSupported by the NationalYouth Fund Program（51677047）.

1674-3814（2016）10-0104-05

TM76；TP393.08

A

2016-02-29。

王国欢（1963—），男，高级工程师，研究方向为信息管理；

李 敏（1970—），女，硕士，高级工程师，研究方向为信息管理；

陶振文（1972—），男，硕士，高级工程师，研究方向为信息管理。