基于物质点法金属体积成形过程的仿真

谢桂兰 于 超 龚曙光 田 杰 胡骏迪

湘潭大学，湘潭，411105



基于物质点法金属体积成形过程的仿真

谢桂兰 于 超 龚曙光 田 杰 胡骏迪

湘潭大学，湘潭，411105

针对传统有限元法开展金属体积成形分析过程中存在的网格畸变，以及在常规无网格法分析中存在的本质边界条件施加困难等问题，建立了基于物质点法金属体积成形过程的仿真模型。因其背景网格积分采用了有限元形函数，从而有效地解决了边界条件施加困难的问题。通过对圆柱顶镦和反向挤压等金属体积成形过程的仿真，并将仿真结果与实验和有限元结果进行了对比分析，结果显示物质点法不仅能有效地消除网格畸变，而且在金属发生大变形时其计算精度优于有限元法的计算精度。所得结论可为物质点法在弹塑性大变形分析中的应用提供指导。

物质点法；弹塑性大变形；金属体积成形；数值模拟

0 引言

金属体积成形是固态金属材料成形的主要方式，其成形过程属于几何非线性和物理非线性的大变形问题。目前有限元(finite element,FE)数值模拟技术是金属体积成形问题广泛采用的分析方法，但由于有限元法依赖于网格，在开展大变形分析时易产生网格畸变，从而造成计算失败，故需要对其进行网格重构，同时新旧网格节点场量映射会降低其计算效率与精度[1-2]。针对有限元法的不足，近年来SPH(smooth particle hydrodynamics)[3]、RKPM(reproducing kernel particle method)[4]、EFG(element free Galerkin method)[5]等无网格法在计算金属体积成形问题中得到广泛应用，但它们存在本质边界条件施加困难[6]、粒子响域搜索费时[7]、积分时间步长随粒子间距减小而减小[8]等不足。

Sulsky等[9]提出了一种新型的数值方法即物质点法(material point method, MPM)。它将材料域离散成质点集合，质点携带所有的物质信息如质量、速度、应力、应变等，且用质点的运动来描述材料的流动与变形，同时采用规则背景网格来计算空间导数和求解动量方程[10]。目前物质点法已在高速碰撞[11]、爆炸[12]、动态裂纹扩展[13]等领域得到应用。Wieckowski[14]借助MPM研究了颗粒材料流动、金属材料切削等问题；Carter等[15]采用MPM模拟了沙粒崩溃现象；Nair等[16]针对广义物质点法提出了一种隐式时间积分方法，并应用于超弹性问题的求解。鉴于MPM具有拉格朗日和欧拉算法的优势，非常适合模拟涉及材料特大变形的断裂破碎等问题，本文开展了基于MPM的金属体积成形的仿真研究。

1 物质点法(MPM)简介

MPM的基本思想是将连续体离散成若干个集中质量的物质点集合，并按照连续体的形状分布在背景网格内，在整个计算过程中，物质点和背景网格节点之间应用节点形函数完成两次映射计算并采用显式时间积分算法求解，以实现各物质点应力和应变的更新。图1为物质点法离散示意图。其理论推导见文献[9-10]。

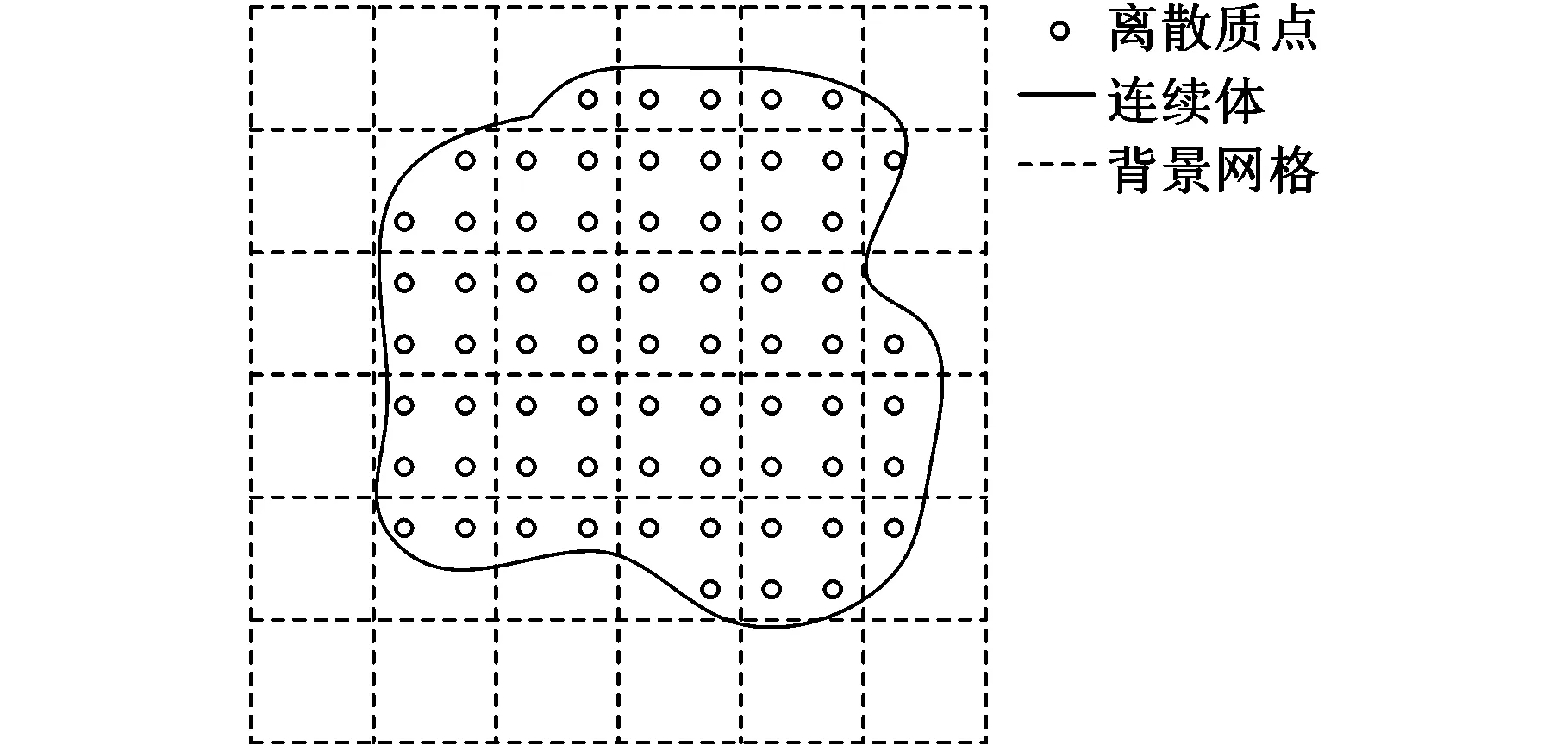
图1 物质点法示意图

采用MPM求解时，连续体满足下面的控制方程(不考虑热量交换)。

动量方程：

ρa=·σ+ρb

(1)

质量守恒方程：

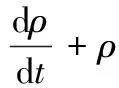
(2)

式中，ρ为密度；a为加速度矢量；v为速度矢量；σ为柯西应力张量；b为单位质量上的体积力。

任取试函数w代入式(1)得动量方程的弱形式为

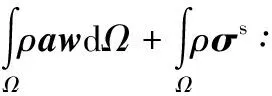
(3)

式中，Ω为当前构形；σs为比应力；ts为比边界面力。

当材料域用质点离散时，连续体的密度等于所有物质点质量之和，写成δ函数为

(4)

式中，Np为质点总数；mj为质点j的质量；δ为Dirac Delta函数；xij为t时刻质点j的坐标。

将式(4)代入式(3)，积分形式转变为求和形式：

(5)

式中，h为假想的边界层厚度。

物质点法在背景网格上计算动量方程，通过背景网格节点的形函数NI(x)来实现质点与背景网格之间的相互映射。对于三维问题背景网格采用规则八节点六面体，其形函数为

(6)

I=1,2,…,8

其中,ξI、ηI、ζI分别是网格节点I的自然坐标。由于形函数NI(x)兼具紧支性和插值性，故质点xp的影响域是其所在网格单元，同时也消除了无网格法中本质边界条件施加困难的缺陷。

质点的任意某参数cp可通过背景网格节点相应的参数cI插值得到：

(7)

(8)

其中，Ng是背景网格单元节点总数，NIp=NI(xp)表示网格节点I的形函数在质点p处的值，c参数可以代表位移、加速度、速度等。

将式(5)中质点位移、加速度以及试函数由背景网格节点的插值替代，整理得

(9)

J=1,2,…,Ng

(10)

(11)

(12)

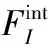
为了加快求解速度，采用集中质量矩阵元素：

(13)

则动量方程式(9)简化为

(14)

I=1,2,…,Ng

MPM通过在背景网格上求解动量方程即式(14)，获得网格节点运动信息并返回质点，用来更新质点的运动状态以及应力应变等。因为背景网格每次参加计算后都可重新生成，所以变形不会累加，网格不会发生畸变。

2 金属成形的MPM仿真模型

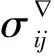
(15)

σijp=Sijp+σmpδij

(16)

采用J2流动理论的径向返回算法[17]对应力进行更新,返回映射法由弹性预测步和塑性修正步组成，在弹性预测步中有

(17)

(18)

将式(17)和式(18)代入式(15)得到应力更新格式：

(19)

(20)

(21)

(22)

(23)

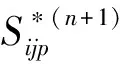
(24)

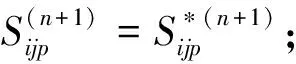
(25)

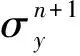
根据物质点法的基本理论及金属体积成形的仿真模型，利用FORTRAN语言编写了金属体积成形MPM程序。下面采用编写的程序分别对棒材顶镦和反向挤压两种工艺过程进行仿真模拟。

3 棒材顶镦工艺过程模拟

图2为棒材顶镦成形过程示意图。选用文献[18]中的几何参数和材料模型，已知圆棒坯料初始尺寸为φ20 mm×49.69 mm，凹模型孔尺寸为φ20 mm×20 mm。坯料材料为AlMgF10，材料在室温下的应力应变关系为σ=180.65×106ε0.183(Pa)。

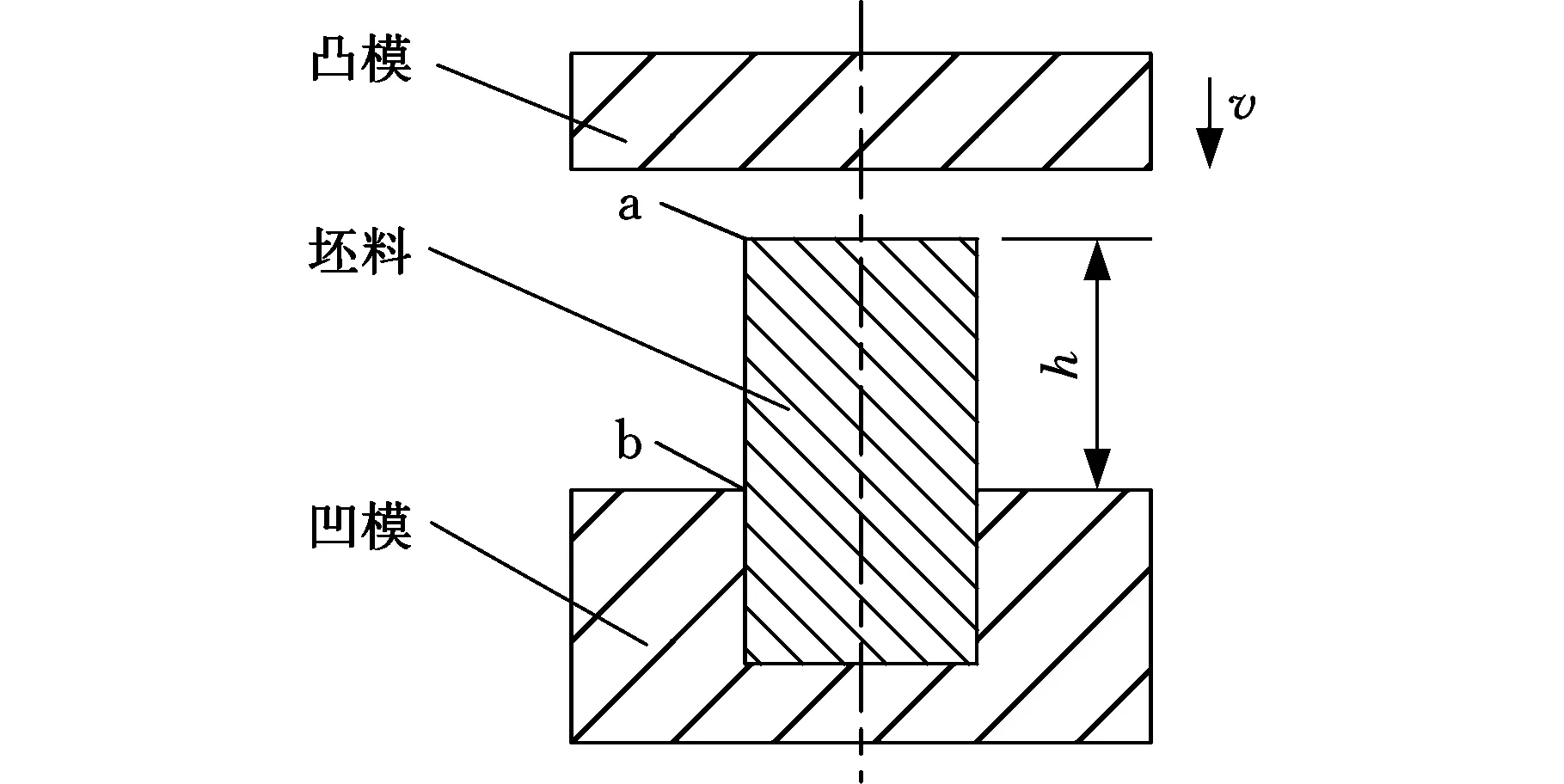
图2 圆棒顶镦模型

凹模固定不动，凸模向下运动，下降速度v=5 m/s。凸模和凹模简化为刚体，模具与工件的摩擦采用库仑摩擦，摩擦因数取0.12。根据模型的对称特点，本文采用1/4模型，棒材被均匀离散成11 067个质点，如图3a所示。通过仿真分析得到自由段高度方向的变形比(D=Δh/h)分别为40%、50%、60%的结果如图3b～3d所示。图4所示为文献[18]的实验结果。

(a)D=0 (b)D=40% (c)D=50% (d)D=60%图3 圆棒在不同变形程度下的结果

图4 文献[18]实验结果

对比图3和图4可知，本文MPM计算所得的工件变形与实验结果相吻合，质点的排布也符合金属流动规律，圆棒下端由于凹模的固定作用而保持不变，上端材料沿径向流动，从而形成了顶镦件的头部。

为进一步研究工件与模具在a和b接触处的金属流动规律，设RS=Ra/R0，RI=Rb/R0，其中，Ra、Rb分别为圆棒在位置a和b处的半径，R0为圆棒初始半径。RS、RI随下压行程s的变化曲线如图5所示。

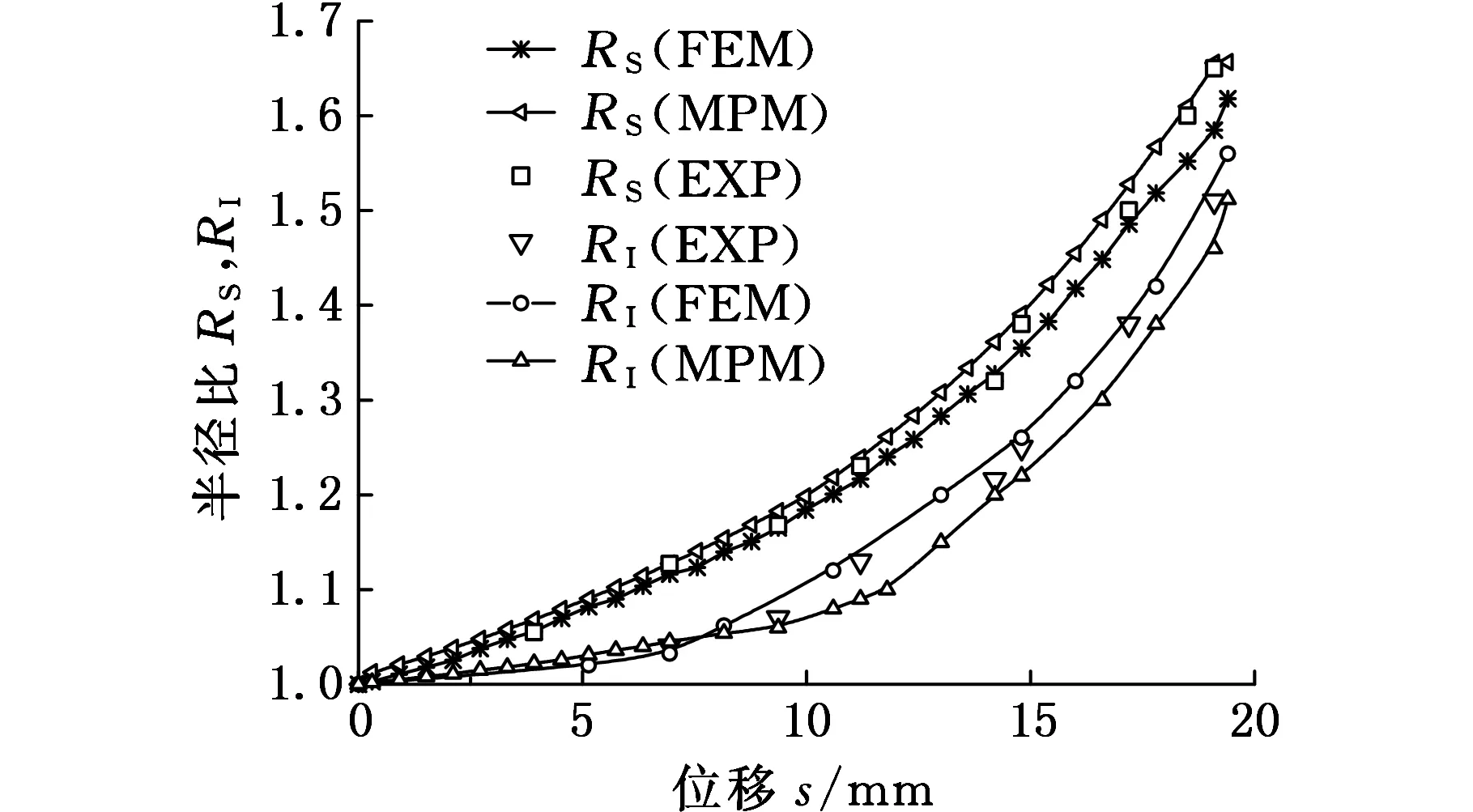
图5 RS和RI随下压行程的变化曲线

从图5可看到，MPM得到的RS、RI曲线与实验结果相吻合，而FEM在下压量小时结果也相吻合。但随着下压量增大，利用FEM得到的RS、RI曲线与实验结果产生了偏离，这主要是因为随着下压量增大，坯料的变形程度增加，此时FEM网格发会生畸变，需要不断地进行网格重构。

圆棒在顶镦时头部变形呈鼓形。压下量不同时MPM与FEM计算结果的最大鼓形半径对比见表1。从表1中得知，MPM结果与FEM结果吻合较好，最大误差为0.62%。

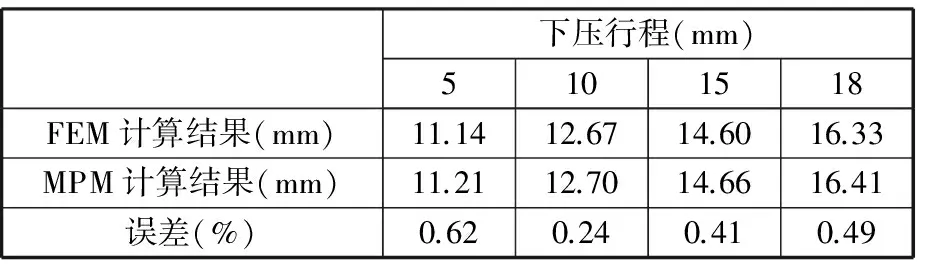
表1 最大鼓形半径

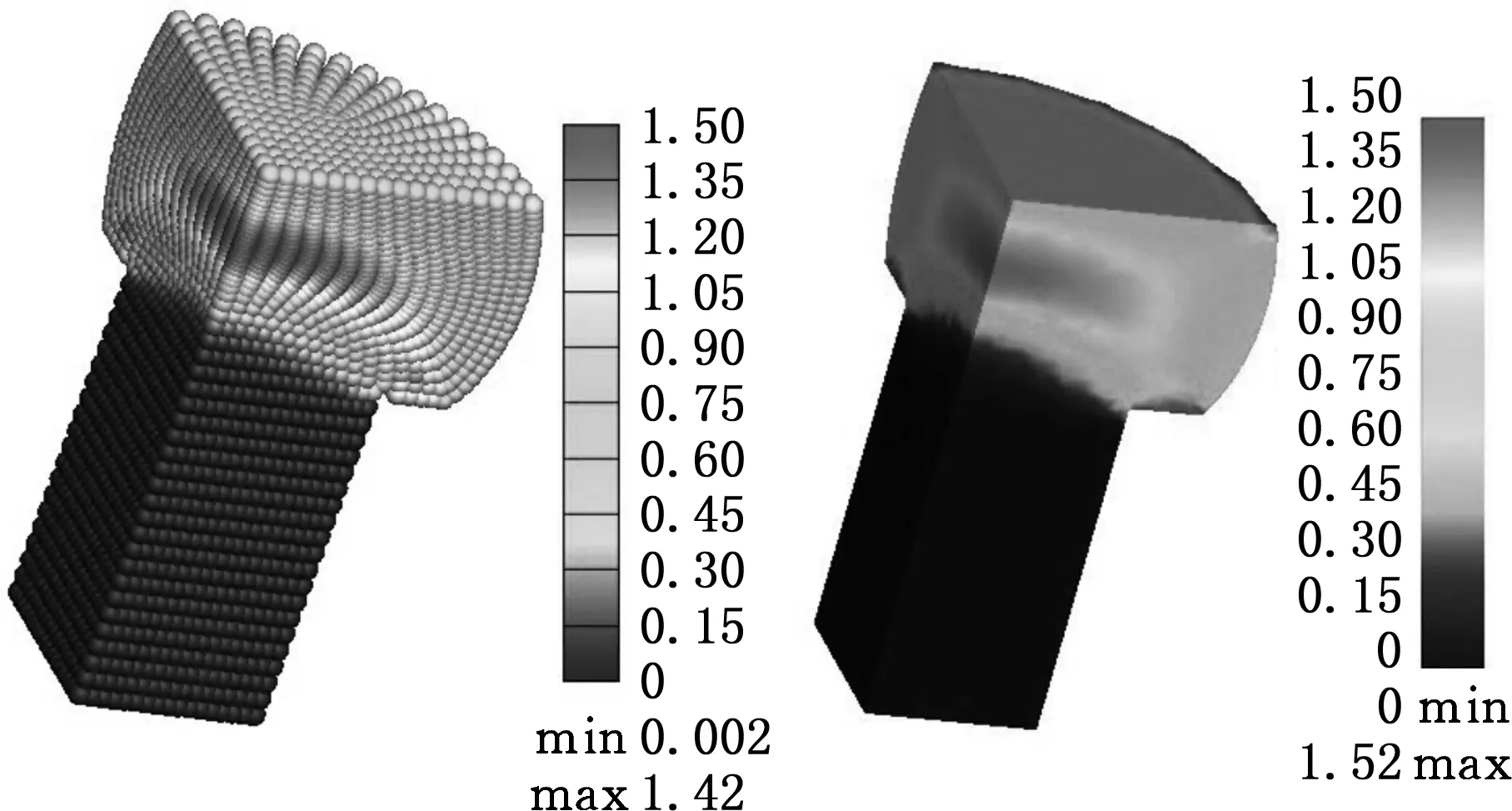
(a)MPM (b)FEM图6 等效应变分布云图

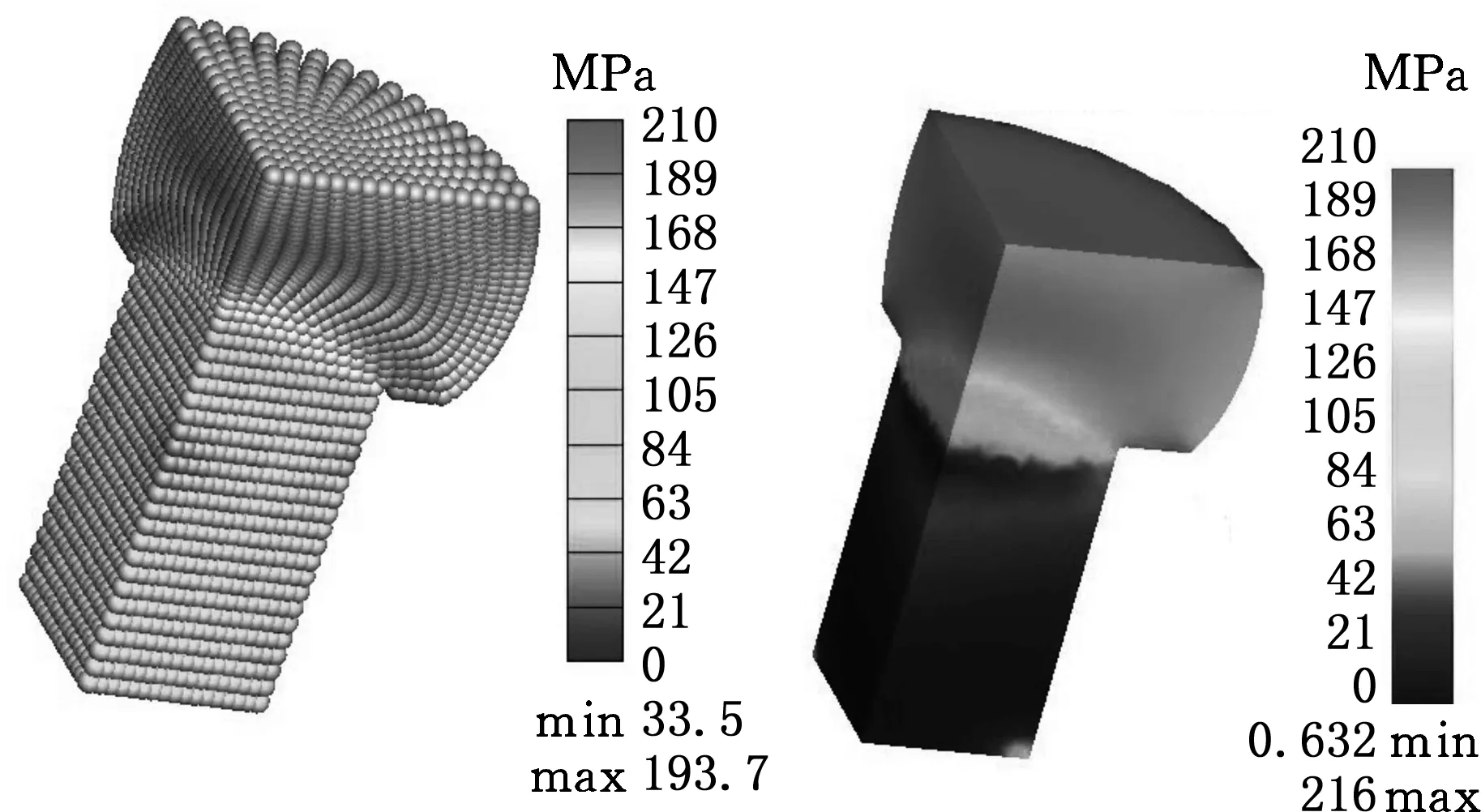
(a)MPM (b)FEM图7 等效应力分布云图

D=60%时MPM和FEM计算得到的等效应变和应力的云图分别见图6和图7。比较图6与图7可知，MPM计算所得的应力应变与FEM计算所得到的结果相近，即工件的自由段由于缺少约束，其变形比较大，最大的应变在自由段的中间部位，锻件下端由于凹模的固定作用，故其应变很小。

4 反挤压工艺过程模拟

金属坯料三维反挤压的成形模型及尺寸如图8所示。工件材料参数如下：弹性模量E=117 MPa，初始屈服应力σ0=400 MPa，硬化模量H=100 MPa，密度ρ=8930 kg/m3，泊松比μ=0.35。凸模和凹模简化为刚体，凹模固定，凸模以v=5 m/s的速度向下挤压工件。采用库仑摩擦，摩擦因数取0.12。为验证MPM仿真金属大变形成形过程的有效性，暂不考虑变形过程中的材料失效。

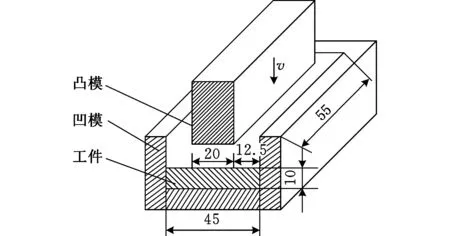
图8 金属反挤压成形过程的物理模型和尺寸

工件在不同压下量Δh时，FEM与MPM的计算结果分别如图9所示。

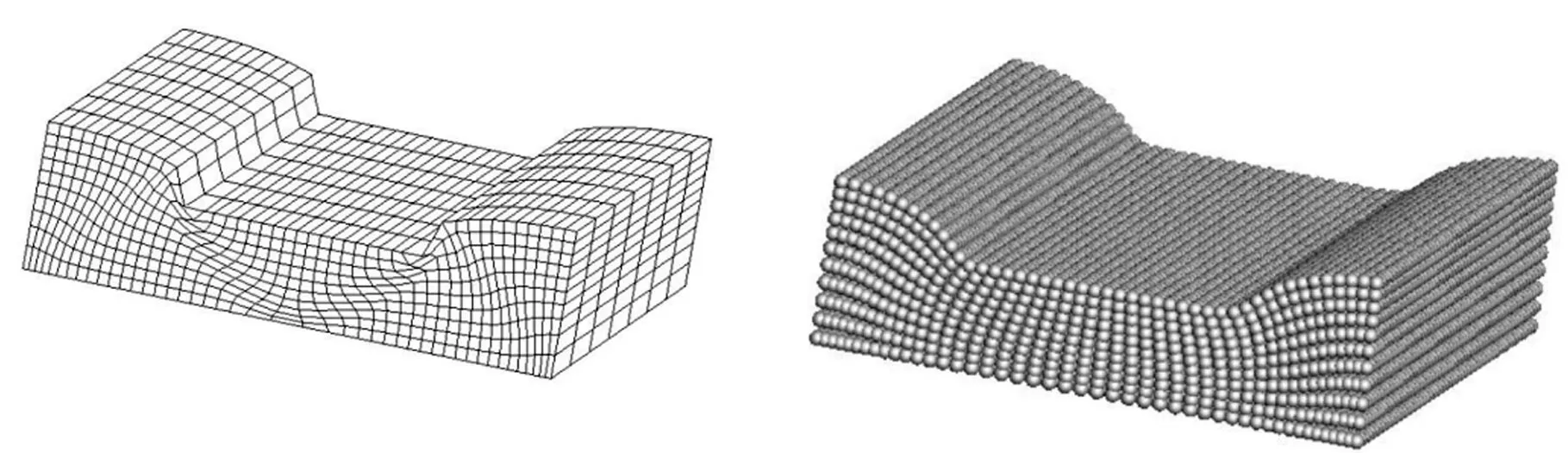
(a)FEM(Δh=2 mm) (b)MPM(Δh=2 mm)

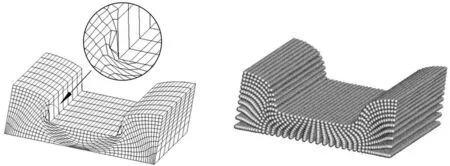
(c)FEM(Δh=4 mm) (d)MPM(Δh=4 mm)图9 不同Δh下反挤压模拟结果

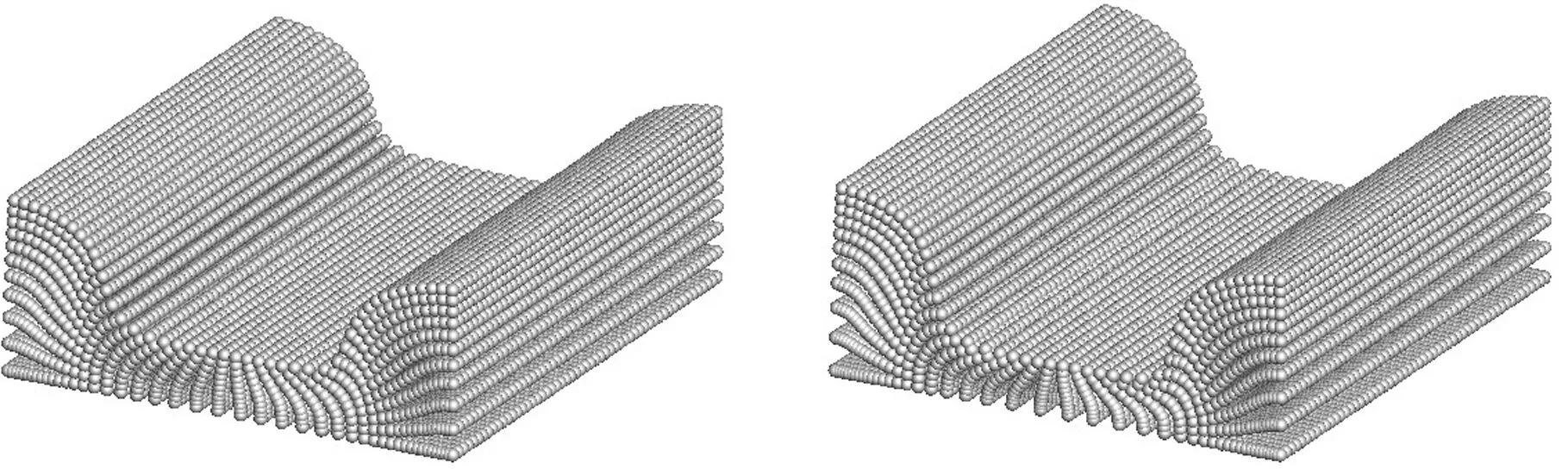
(a)Δh=4.5 mm (b)Δh=5.5 mm

从图9可以看出，当垂直压下量Δh较小时，MPM和FEM均能得到很好的结果。但随反向挤压垂直压下量Δh的增大，即当压下量为4 mm时，有限元法计算的网格已发生了严重畸变，需要进行重构才能继续求解，而MPM的计算却不受影响。若继续增大压下量，MPM依然能计算，图10所示为后续挤压时的一些变形结果，该结果与文献[19]相同。

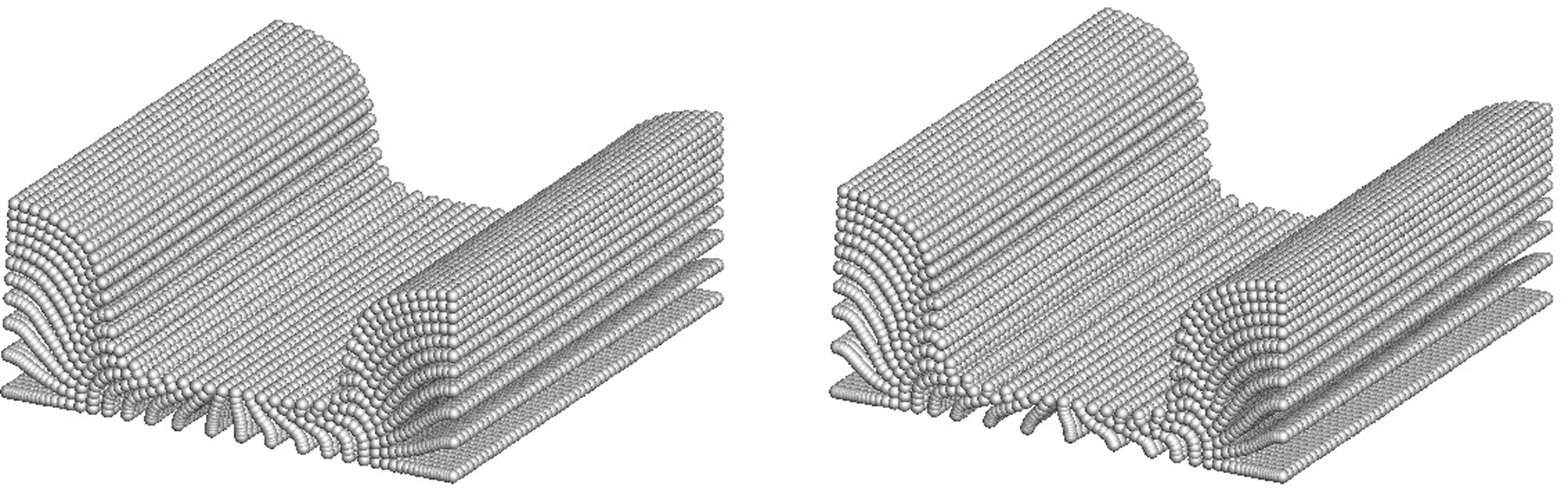
(c)Δh=6 mm (d)Δh=7 mm图10 MPM法模拟反挤压过程结果

从图10可看到，即使工件变形非常大，MPM也能够在不需要任何特殊处理的情况下完成整个反挤压过程的模拟，并且其结果保持光滑，这说明MPM在计算金属大变形时具有较好的优越性。

5 结论

(1)无论是顶镦成形还是反挤压成形，MPM均能得到非常好的仿真结果。

(2)由于MPM在背景网格的计算中采用有限元形函数，故MPM能克服传统无网格法中施加本质边界条件困难的问题。

(3)MPM能克服有限元法在模拟材料大变形时所出现的网格畸变，当材料发生非常大的变形时MPM不需要任何特殊处理就能一次性完成整个计算过程，说明MPM在模拟金属塑性大变形问题时具有较大的优势。

[1] 刘玉红, 李付国, 吴诗惇. 体积成形数值模拟技术的研究现状及发展趋势[J].航空学报, 2002, 23(6): 547-551. Liu Yuhong, Li Fuguo, Wu Shichun. Numerical Simulation for Bulk Forming Process: Its Current Status and Future Progress[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(6): 547-551.

[2] 齐会萍, 李永堂, 华林, 等. 环形零件辗扩成形工艺研究现状与发展趋势[J]. 机械工程学报, 2014, 50(14): 75-80. Qi Huiping, Li Yongtang, Hua Lin, et al. Research Status and Developing Trends on the Rolling Forming Process of Ring Parts[J]. Journal of Mechanical Engineering. 2014, 50(14): 75-80.

[3] 朱蒙蒙，谢桂兰，曹尉南，等. 无网格SPH法在金属镦粗成形中的应用[J]. 热加工工艺,2012,41(5): 20-23. Zhu Mengmeng，Xie Guilan，Cao Weinan，et al. Application of Smooth Particle Hydrodynamic in Metal Forging[J]. Hot Working Technology,2012,41(5): 20-23.

[4] 刘永辉，陈军. 任意模具形状的金属三维体积成形过程刚塑性无网格RKPM分析方法[J]. 塑性工程学报, 2008, 15 (3): 105-109. Liu Yonghui, Chen Jun. Rigid-plastic Reproducing Kernel Particle Method for Three-dimensional Bulk Metal Forming with Arbitrarily-shaped Dies[J]. Journal of Plasticity Engineering,2008, 15(3): 105-109.

[5] 康永林，朱国明，陈伟. LS-DYNA无网格伽辽金方法在轧制过程三维仿真分析中的应用[J]. 塑性工程学报, 2007, 14(4): 140-146 Kang Yonglin, Zhu Guoming, Chen Wei. EFG Method’s Application in the 3D Simulation of Rolling Process in LS-DYNA[J]. Journal of Plasticity Engineering,2007, 14(4): 140-146.

[6] 崔青玲，李长生，刘相华，等. 无网格法及其在金属塑性成形中的应用[J]. 塑性工程学报，2005, 12(1): 38-42. Cui Qingling，Li Changsheng，Liu Xianghua，et al. Meshless Methods and Its Application in Metal Forming[J]. Journal of Plasticity Engineering，2005, 12(1): 38-42.

[7] Ma S, Zhang X, Qiu X M. Comparison Study of MPM and SPH in Modeling Hypervelocity Impact Problems[J]. International Journal of Impact Engineering，2009, 36(2): 272-282.

[8] Smolinski P, Palmer T. Procedures for Multi-time Step Integration of Element-free Galerkin Methods for Diffusion Problems [J]. Computers & Structures，2000, 77(2): 171-183.

[9] Sulsky D, Chen Z, Schreyer H L. A Particle Method for History-dependent Materials [J]. Computer Methods in Applied Mechanics and Engineering,1994, 118(1/2): 179-196.

[10] 廉艳平，张帆，刘岩，等. 物质点法的理论和应用[J].力学进展,2013,43(2): 237-264. Lian Yanping,Zhang Fan,Liu Yan,et al.Material Point Method and Its Applications[J].Advances in Mechanics,2013,43(2): 237-264.

[11] 马上，张雄，邱信明. 超高速碰撞问题的三维物质点法[J]. 爆炸与冲击,2006，26(3): 273-278. Ma Shang，Zhang Xiong，Qiu Xinming. Three-dimensional Material Point Method for Hypervelocity Impact[J]. Explosion and Shock Waves,2006，26(3): 273-278.[12] 王宇新，陈震，孙明. 滑移爆轰问题无网格MPM法数值模拟[J].力学与实践,2007, 29(3): 20-25. Wang Yuxin，Cheng Zhen，Sun Ming. Numerical Simulation of Slippage Detonation by Material Point Method-MPM[J]. Mechanics in Engineering, 2007, 29(3): 20-25.

[13] Guo Y J, Nairn J A. Three-dimensional Dynamic Fracture Analysis Using the Material Point Method[J]. Computer Modeling in Engineering and Sciences,2006, 16(1): 141-155.

[14] Wieckowski Z. The Material Point Method in Large Strain Engineering Problems[J]. Computer Methods in Applied Mechanics and Engineering,2004, 193(39/41): 4417-4438.

[15] Carter M M, Pedro A, Peter M H, et al. Simulation Granular Column Collapse Using the Material Point Method[J]. Acta Geotechnina, 2014, 10(1):101-116.

[16] Nair A,Roy S.Implicit Time Integration in the Generalized Interpolation Material Point Method for Finite Deformation Hyperelasticity[J]. Mechanics of Advanced Material and Structures, 2012, 19(6): 465-473.

[17] 张雄,王天舒.计算动力学[M].北京:清华大学出版社,2007.

[18] Xiong S, Li C S, Rodrigues J M C, et al. Steady and Non-steady State Analysis of Bulk Forming Processes by the Reproducing Kernel Particle Method[J]. Finite Elements in Analysis and Design,2005, 41(6): 599-614.

[19] Li G, Belytschko T. Element-free Galerkin Method for Contact Problems in Metal Forming Analysis[J]. Engineering Computations, 2001, 18(1/2): 62-78.

(编辑 陈 勇)

Simulation of Metal Bulk Forming Based on MPM

Xie Guilan Yu Chao Gong Shuguang Tian Jie Hu Jundi

Xiangtan University,Xiangtan,Hunan,411105

Aiming at the problems that mesh distortions in finite element method(FEM) and difficulties of applying the essential boundary conditions in the traditional mesh-less method when doing the analysis of metal bulk forming process, a simulation model of metal bulk forming process was presented based on MPM. Because the shape function of the finite element method was used on the background grid nodes, MPM might solve the difficulty problems in dealing with the boundary conditions effectively. Two metal bulk forming processes(heading of cylindrical billets and backward extrusion) were performed, compared the results of experiments with those of finite element method, it is shown that MPM may eliminate the mesh distortions, and may get more accurate results than that of the finite element method when large deformations occur. The conclusions may provide guidance for the MPM to be applied in the large elastic-plastic deformation analyses.

material point method(MPM); large elastic-plastic deformation; metal bulk forming; numerical simulation

2016-01-19

国家自然科学基金资助项目(51475403)

TG302

10.3969/j.issn.1004-132X.2016.22.019

谢桂兰，女，1966 年生。湘潭大学机械工程学院教授。主要研究方向为新材料力学性能。发表论文 30 余篇。于 超，男， 1990年生。湘潭大学机械工程学院硕士研究生。龚曙光，男，1964年生。湘潭大学机械工程学院教授。田 杰，男, 1988 年生。湘潭大学机械工程学院博士研究生。胡骏迪，男，1990年生。湘潭大学机械工程学院硕士研究生。