叶片电化学加工过程多场耦合仿真

陈远龙 方 明 裴 迪 常伟杰

合肥工业大学，合肥，230009



叶片电化学加工过程多场耦合仿真

陈远龙 方 明 裴 迪 常伟杰

合肥工业大学，合肥，230009

针对叶片电化学加工过程难以预测、实验参数修正周期长的问题，建立与温度相关的叶片多场耦合仿真模型，基于COMSOL Multiphysics平台对叶片电化学加工过程进行多场耦合仿真，仿真分析了不同加工电压和不同进液流量对法向平衡间隙的影响。结果表明：加工电压越大，间隙也相应增大，且间隙分布越不均匀；进液流量越大，间隙分布越均匀。采用其中一组仿真参数进行工艺实验，仿真与实验的对比结果表明，叶片轮廓曲率变化缓慢处的仿真结果和实验结果比较贴合，而轮廓曲率变化较快处的仿真值与实验值差别相对较大，但两者的变化趋势相同。

叶片；电化学加工；多物理场；耦合仿真

0 引言

叶片是航空发动机的核心零件，随着航空技术的发展，叶片结构向叶身超薄、型面扭曲复杂等方向发展，而叶片所用的材质向钛合金、钴基超耐热合金等难加工材料方向发展。由于电化学加工能高效加工各种难切削金属材料以及复杂形状零件，具有工具无损耗、加工表面质量好等突出优点，被广泛应用于航空发动机叶片的制造中[1-2]。但电化学加工过程非常复杂，涉及电场、流场、温度场等多个物理场，属于典型的多场耦合过程，这使得电化学加工过程难以被准确预测以及工具阴极不能被精确设计[3]。因此，为了获得满足要求的加工参数，需要进行大量的工艺实验，这导致电化学加工的准备周期变长和成本变高，不易于电化学加工的应用推广[4]。针对这一问题，国内外学者对电化学加工的模拟与仿真进行了大量研究，仿真理论模型由最初的纯电场仿真向多场耦合仿真方向发展[5-9]。而目前大多数多场耦合仿真研究只是在加工进入平衡状态下进行阳极型面的预测和阴极形状的设计，对复杂工件型面的成形过程进行仿真却很少涉及，且大多数加工过程多场耦合仿真流场模型采用层流Navier-Stokes方程[10-11]。

本文以叶片电化学加工为研究对象，围绕电场、流场以及温度场等耦合作用对电化学加工成形过程的影响，引入壁函数法与湍流模型相结合的流场模型，建立与温度相关的多场耦合仿真模型，对电化学加工成形过程进行仿真，揭示电化学加工在平衡态和非平衡态过程中阳极轮廓的溶解规律，为工件阳极轮廓的准确预测和工具电极的精确设计提供理论支持，从而提高叶片电化学加工精度，缩短实验周期。

1 理论模型

叶片电化学加工采用单面进给加工方式，供液形式采用侧流式，其加工过程多场耦合仿真几何模型见图1。在叶盆电化学加工几何模型中，电解液从左向右流经加工区；在叶背电化学加工几何模型中，电解液从右向左流经加工区。

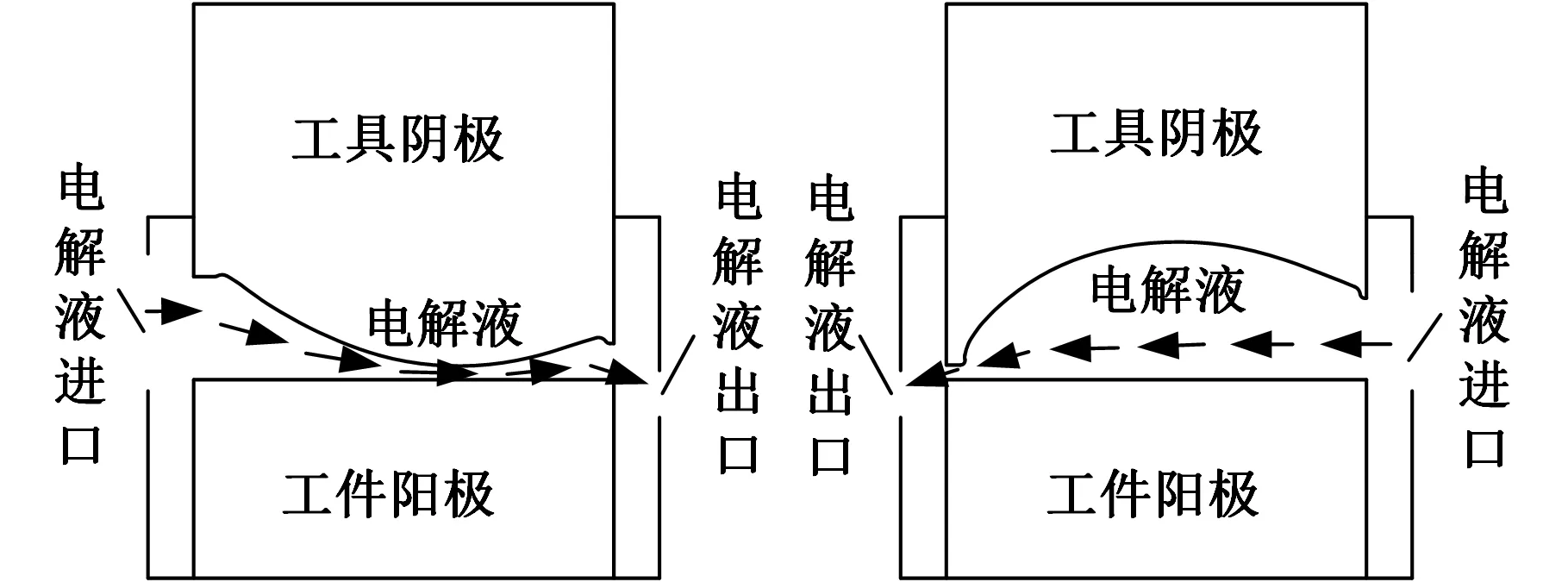
(a)叶盆仿真几何模型 (b) 叶背仿真几何模型图1 叶片电化学加工过程仿真几何模型

1.1 电场模型

假设阴极、阳极表面均为等电位面，忽略电极边界效应，则在电解液中，由电荷守恒可知，电势U满足下式：

·(κU)=0

(1)

式中，κ为电解液电导率。

电解液电导率可由一个温度相关的线性模型来定义[10]：

κ=κ0[1+γ(θ-θ0)]

(2)

式中，θ0为初始温度；γ为温度相关系数；κ0为初始电导率。

1.2 流场模型

在电化学加工过程中，为了有效地带走加工产物和加工过程中产生的热量，整个流道的流体应处于湍流状态。假设电解液为不可压缩流体，则由质量守恒定律和动量守恒定律可知，流体流动满足下式：

(3)

式中，ρ为电解液密度；v为流速；p为电解液压力；μ为电解液动力黏度；μT为湍流黏性系数；k为湍流动能。

综合考虑所研究的湍流类型、计算精度和计算时间，RNS k-ε模型可以很好地满足工程实际需求[12]，其湍流动能方程和耗散率方程如下：

(4)

式中，ε为湍流耗散率； σk、σε、C1s、C2s为模型常数；pk为平均速度梯度产生的湍流动能。

在流道近壁区雷诺数低，湍流发展不充分。因此，在近壁区不能使用RNS k-ε模型来进行计算，而壁函数法消耗的计算资源少，计算成本低，具有很强的工程实用性[13]。所以本文采用壁函数法来求解近壁处湍流流动。

1.3 传热模型

加工间隙内电解液的温度分布可由对流-扩散方程描述[10]：

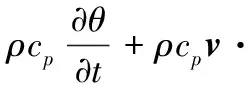
(5)

式中，cp为电解液质量定压热容；kt为电解液热导率；Qbulk为加工中产生的热量。

加工中热量的产生通常由电解液的焦耳热和电极-电解液边界的反应热组成。由于绝大多数反应热通过电极的热传导作用传入电极中，所以其对电解液的影响很小[10]。忽略反应热的影响，则由欧姆定律可知：

Qbulk=QJoule=i·U

(6)

式中，QJoule为电解液焦耳热；i为电流密度。

1.4 阳极溶解模型

随着电化学加工过程的进行，加工区域的几何结构不断变化。由法拉第定律可知，电化学加工阳极溶解速度与电流密度相关，即

υa=ηωin

(7)

式中，υa为阳极材料法向去除速度；η为电流效率；ω为体积电化学当量；in为法向电流密度。

由式(1)可知，法向电流密度in可表示为

(8)

式中，n为阳极-电解液界面边界外法向向量。

由于钛合金、钴基超耐热合金等材料价格昂贵且不易获取，为了实验方便，选用304不锈钢作为工件材料，进行验证实验。查阅相关文献获得其在NaNO3溶液中的电流效率曲线，通过数学拟合得到电流效率曲线近似数学关系如下[7]：

(9)

式中，i为电流值。

2 耦合与仿真

电化学加工过程中，温度场与电场、流场以及几何结构的影响关系如图2所示。由法拉第定律可知，阳极的溶解速度直接取决于加工间隙内电场分布。当加工电压一定时，极间电场分布受电解液电导率和几何结构的影响，而电解液电导率的大小受极间温度分布的影响。因此，电化学加工过程仿真的关键是对加工间隙内温度分布的耦合求解。

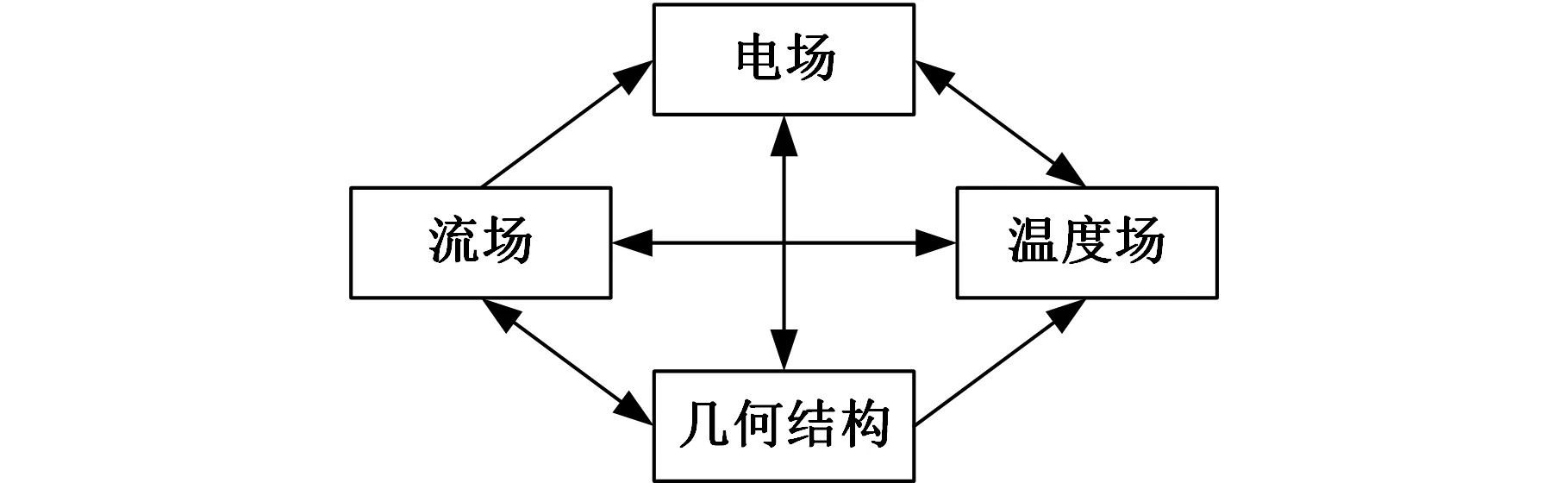
图2 各物理场之间的影响关系

本文通过对流-扩散方程(式(6))的对流项来耦合流场的影响，通过热源项来耦合电场的影响，从而实现对极间温度分布的耦合求解。具体求解过程见图3。

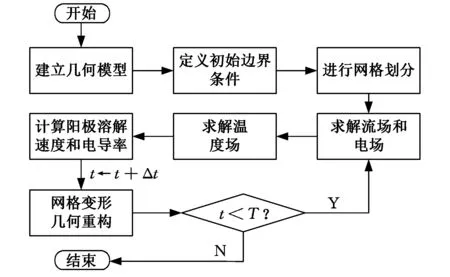
图3 耦合求解流程图

3 仿真分析与实验验证

3.1 叶片加工过程多场耦合仿真

基于COMSOL Multiphysics有限元仿真平台，对叶片电化学加工过程进行多物理场耦合仿真研究。设定初始加工间隙为0.5 mm，加工电压为12 V，阴极进给速度为0.1 mm/min，电解液初始温度为25 ℃，电解液为质量分数为8%的NaNO3溶液(初始电导率为7.2 S/m)，电解液流量为2 kg/s，得到叶盆和叶背轮廓形状及电解液流速分布随加工时间的变化，如图4、图5所示。

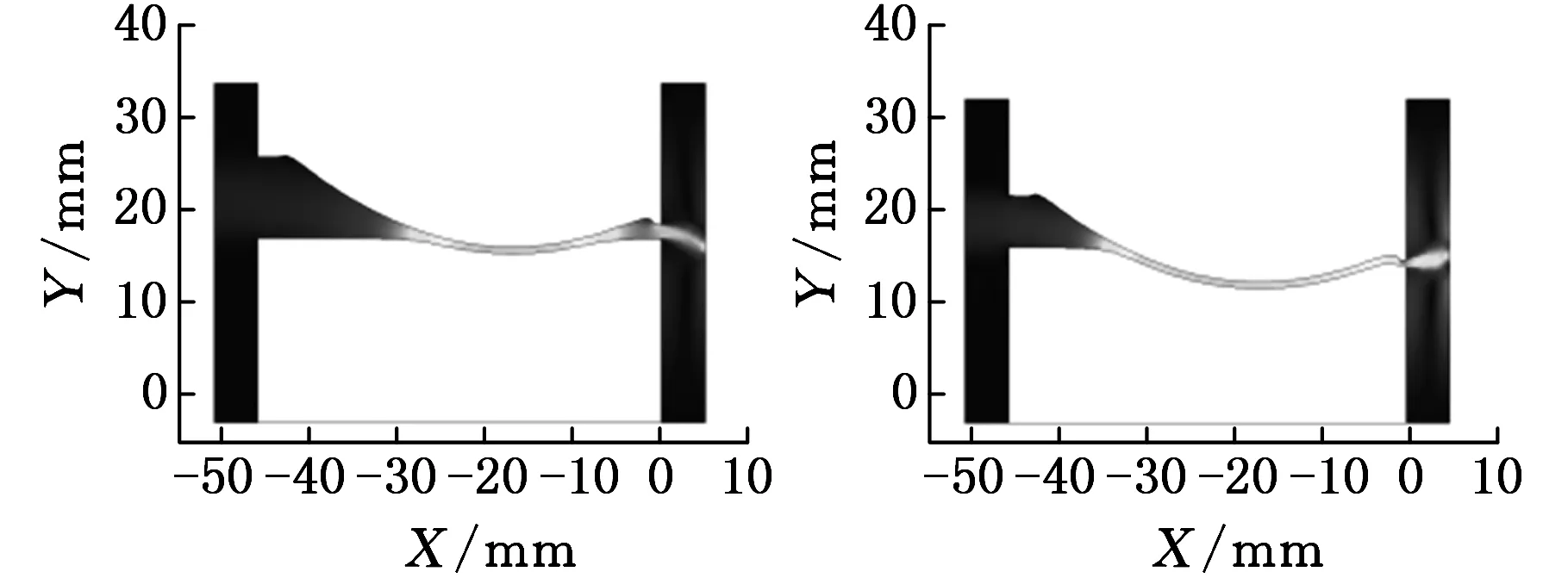
(a)加工600 s (b) 加工1800 s

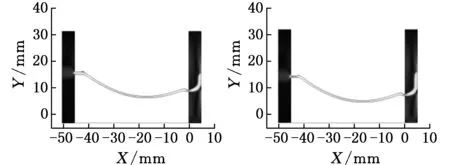
(c)加工3900 s (d)加工4700 s图4 叶盆轮廓随加工时间的变化

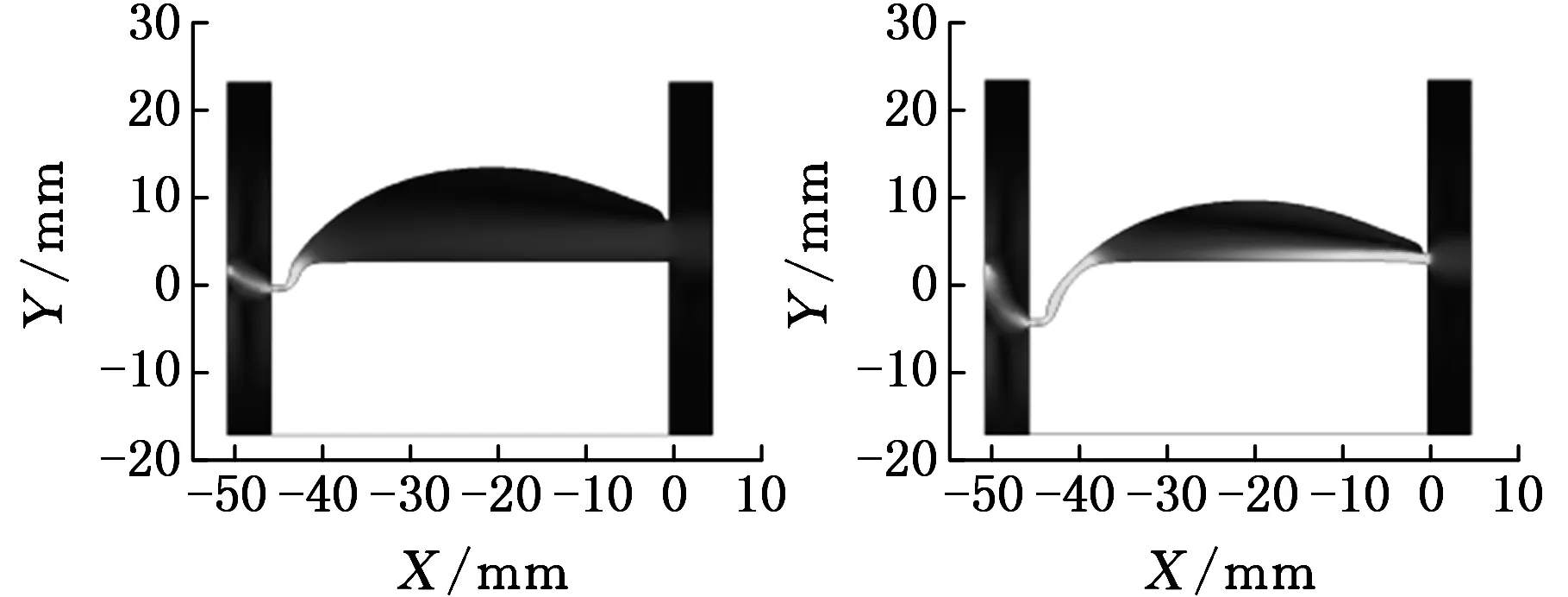
(a)加工1300 s (b) 加工2900 s

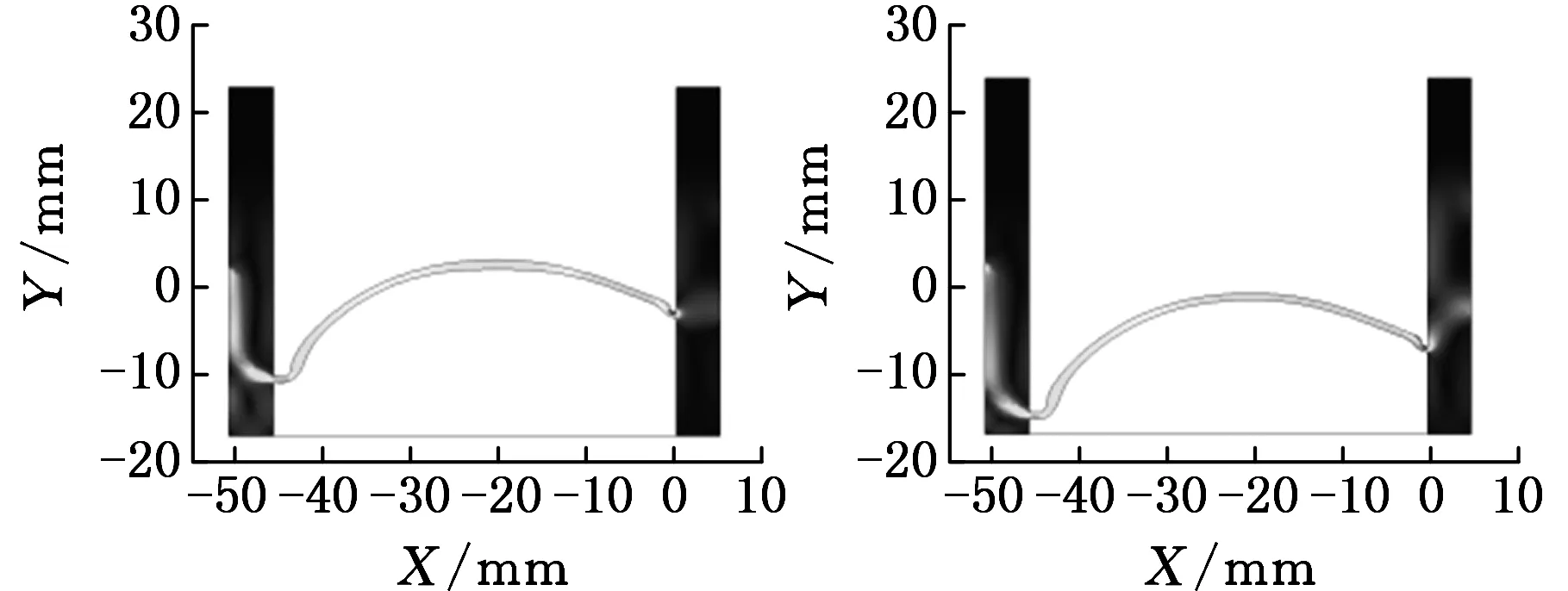
(c)加工5300 s (d)加工7180 s图5 叶背轮廓随加工时间的变化

从图4知，叶盆轮廓最低点最先进入平衡状态，随着加工的进行，叶盆在该点两侧位置也逐渐进入平衡状态。当整个加工过程进入平衡状态时，极间间隙内电解液的流速分布趋于均匀。

从图5知，叶背轮廓左侧最先进入平衡状态，随着加工的进行，叶背进入平衡状态的位置由两侧向中间变化。当整个加工过程进入平衡状态时，极间间隙内电解液的流速分布趋于均匀，但叶背左侧位置电解液流速低于中间位置电解液流速。

3.2 不同加工电压的多场仿真结果

进给速度为0.3 mm/min，电解液参数同上，进液流量qm为4 kg/s，选用不同加工电压U进行叶片电化学加工多场耦合仿真，并在仿真后的叶片轮廓上取10个测量点，测量点位置和仿真电解液流向如图6所示，得到极间温度分布和法向平衡间隙随加工电压的变化如图7和图8所示。

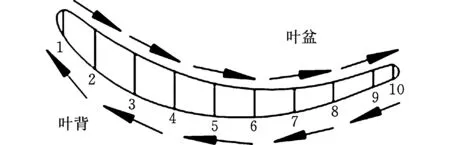
图6 电解液流向与叶片轮廓测量点位置

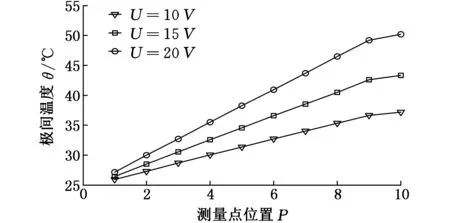
(a)叶盆极间温度随加工电压的变化

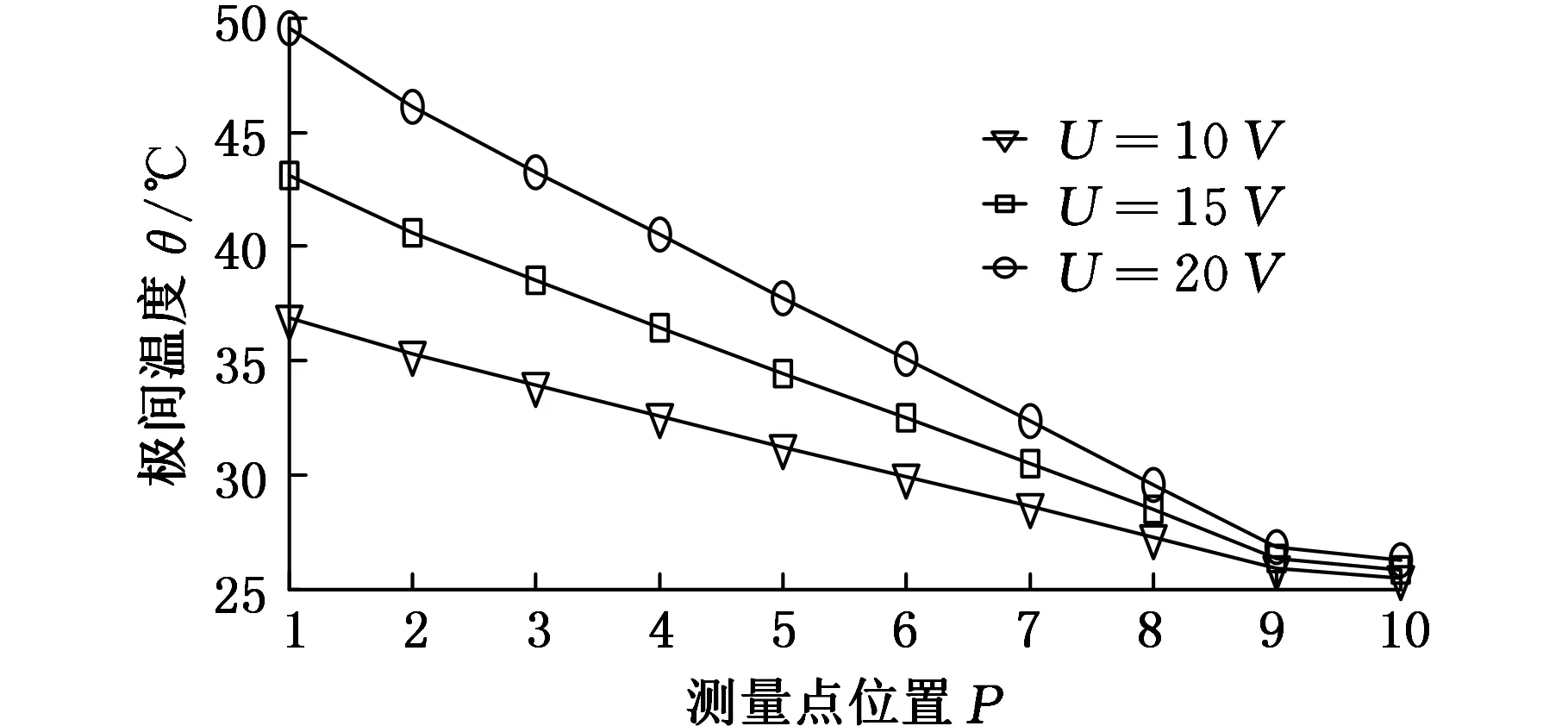
(b)叶背极间温度随加工电压的变化图7 极间温度随加工电压的变化

由图7可知，沿着流程方向，极间温度逐渐升高，且随着加工电压的增加，极间温度也相应升高。当加工电压由10 V增加到20 V时，叶盆在测量点1与10处温度差由11.2 ℃增加到23.1 ℃，叶背在两处温度差由11.4 ℃增加到23.3 ℃，即相同参数条件下，加工电压越大，极间温度分布越不均匀，从而导致极间电导率分布也越不均匀。

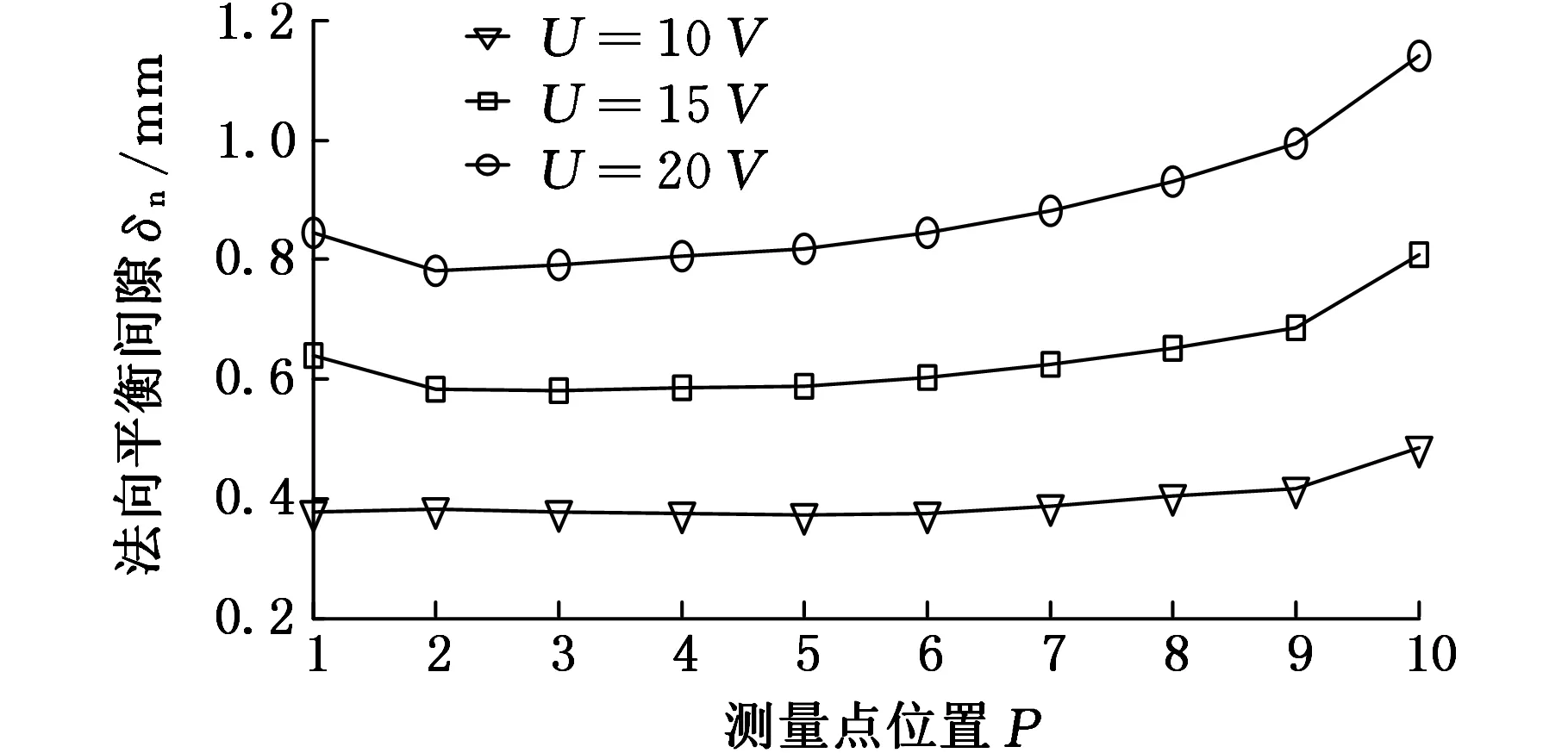
(a)叶盆法向平衡间隙随加工电压的变化

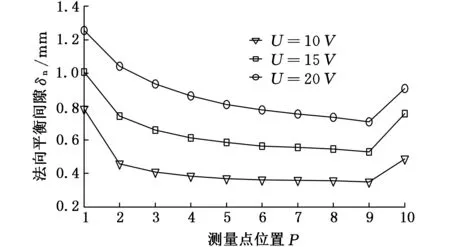
(b)叶背法向平衡间隙随加工电压的变化图8 法向平衡间隙随加工电压的变化

由图8可知，随着加工电压的变大，法向平衡间隙也相应变大，而极间间隙分布均匀度却变差。在叶片进排气边位置(测量点1和10)，法向平衡间隙增幅较大，尤其是在电解液出口侧(测量点1)。由于在进排气边处，叶片轮廓法线方向与阴极进给方向夹角较大，造成已加工面发生侧面腐蚀而使其间隙变大，而由图7可知，在出液口侧，电解液温度高于其他位置温度，从而加剧了侧面腐蚀。

3.3 不同进液流量的多场仿真结果

加工电压为15 V，进给速度为0.6 mm/min，电解液参数同上，选用不同进液流量进行叶片电化学加工多场耦合仿真，得到极间温度和法向平衡间隙随进液流量的变化，如图9、图10所示。

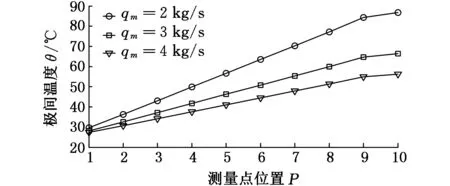
(a)叶盆极间温度随进液流量的变化

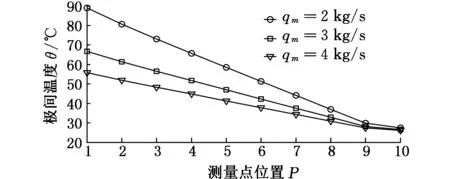
(b)叶背极间温度随进液流量的变化图9 极间温度随进液流量的变化

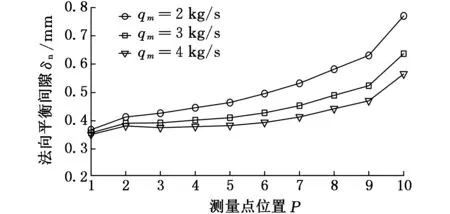
(a)叶盆法向平衡间隙随进液流量的变化

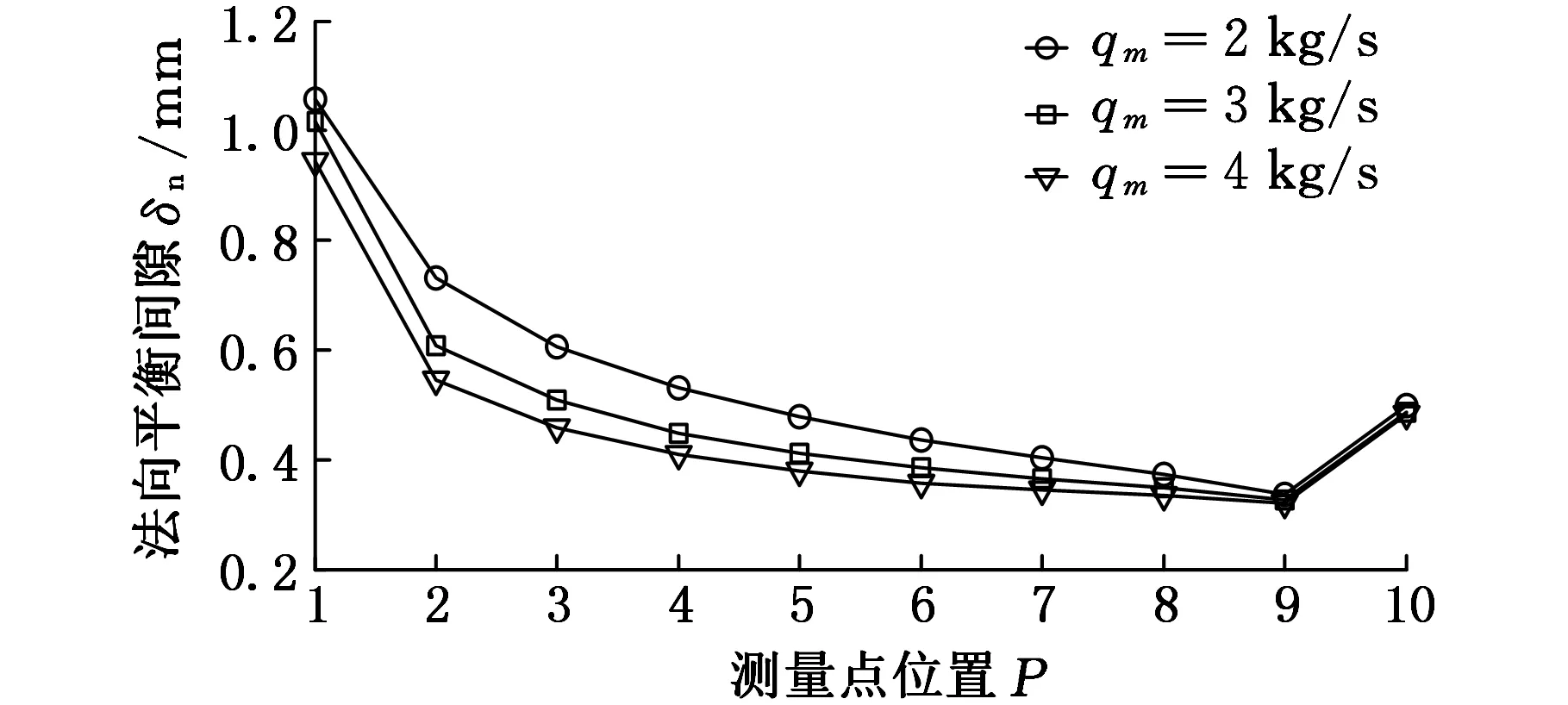
(b)叶背法向平衡间隙随进液流量的变化图10 法向平衡间隙随进液流量的变化

由图9知，沿电解液流程方向，电解液温度逐渐升高，且随着进液流量的减小，温度升高越快。当进液流量为2 kg/s时，在测量点10处叶盆极间温度高达86.6 ℃，在测量点1处叶背极间温度高达89.1 ℃。

由图10可知，法向平衡间隙沿流程方向逐渐增大，且随着进液流量的增大，间隙逐渐减小。这是因为随着进液流量的变大，对流作用逐渐增强，进而带走更多的热量，使电解液电导率变小，从而引起间隙的减小。而在叶背进液口位置，从测量点10到测量点9间隙减小了0.16 mm，这是因为在进液口位置，电解液温度温升较小，对间隙的影响较弱，而测量点10处阴极进给方向与轮廓法向夹角比测量点9处要大，使得测量点10处间隙要大于测量点9处间隙。

3.4 叶片电化学加工实验验证

选用进液流量为2 kg/s，加工电压为12 V，阴极进给速度为0.1 mm/min，电解液采用质量分数为8%的NaNO3溶液，初始加工间隙为0.5 mm，进行叶片电化学加工过程多场耦合仿真，并采用相同加工参数进行实验验证，实验装置如图11所示。

图11 实验装置

运用德国ZEISS公司生产的MC850三坐标测量机对加工后的叶片轮廓进行测量(图12)，测量点位置如图6所示。实验结果与仿真结果的对比如图13所示。

图12 叶片轮廓的检测

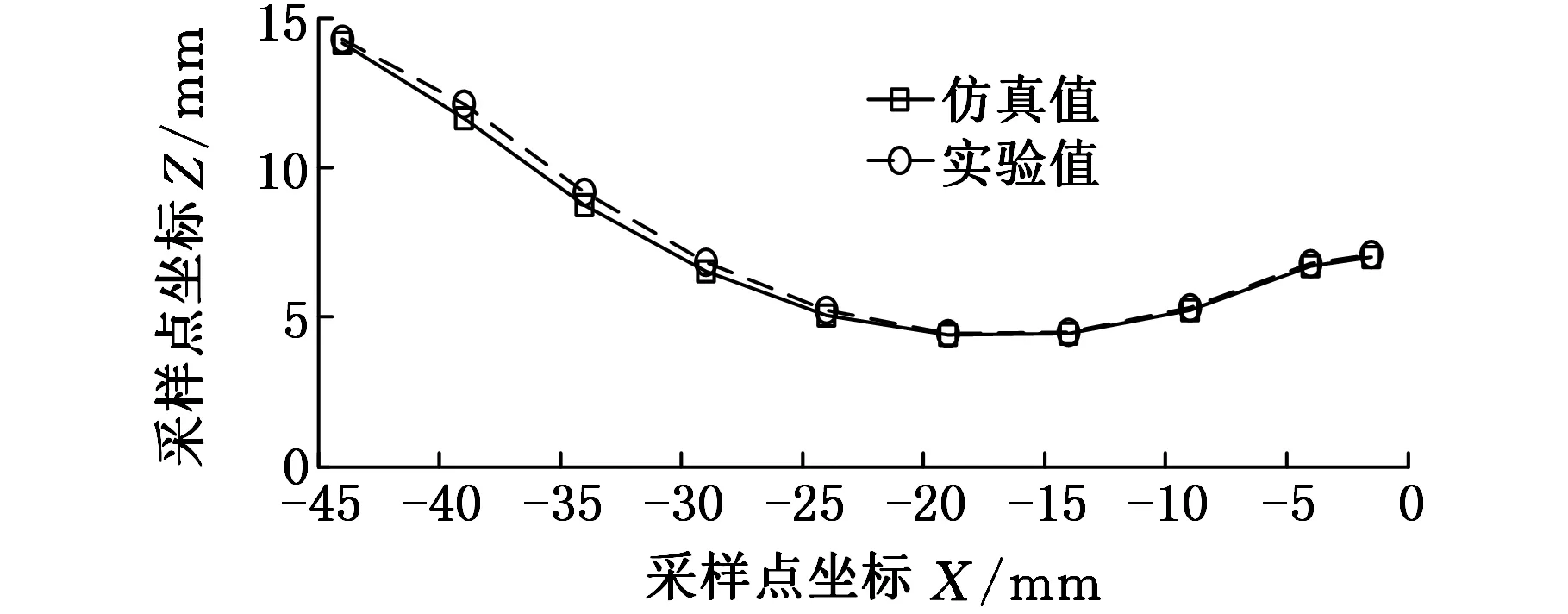
(a)叶盆仿真与实验结果对比

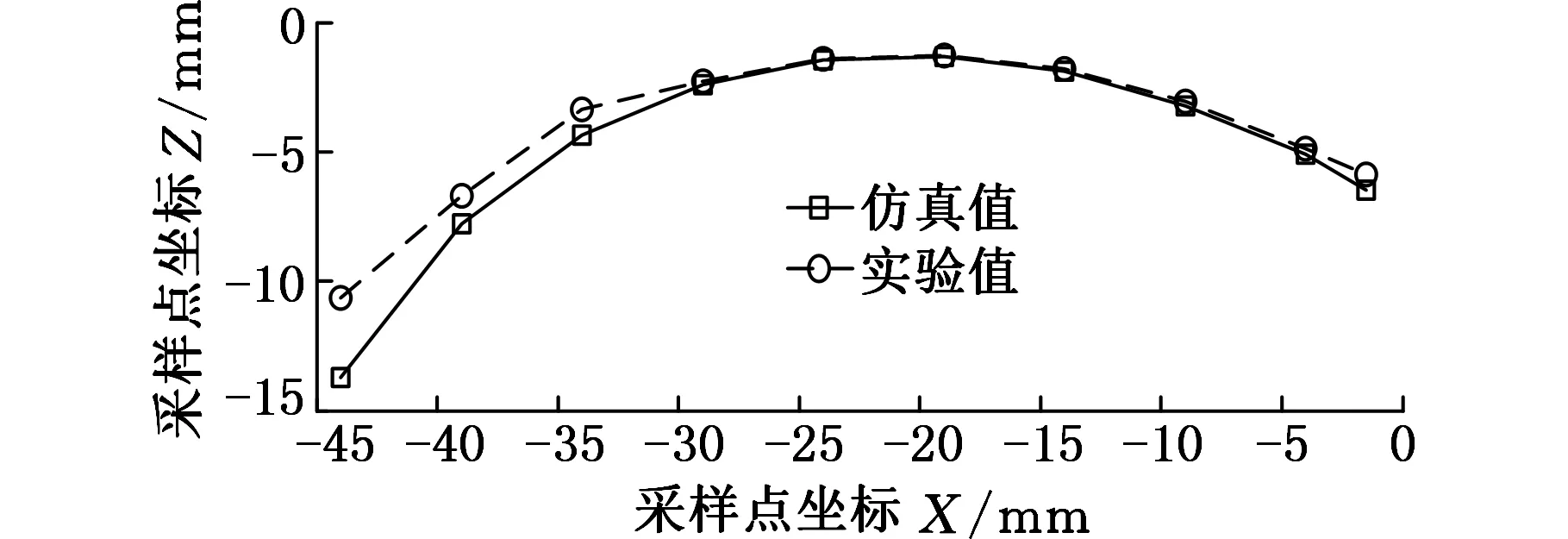
(b)叶背仿真与实验结果对比图13 叶片仿真与实验结果对比

由图13可得，叶盆的轮廓仿真值与实验值比较吻合，而叶背的轮廓仿真值与实验值在轮廓法向与进给方向夹角较小处比较贴合，在夹角较大处误差相对较大，特别是叶背轮廓的测量点1处。由仿真与实验结果分析可知，造成误差的主要原因是叶背轮廓曲率变化缓慢的地方，电解液流动顺畅；在夹角较大处，轮廓曲率变化较快，加工产生的气泡容易在此堆积，造成电解液电导率下降，从而使阳极材料去除量减小，由于本次多场耦合仿真着重研究温度对电化学加工过程的影响，并没有考虑气泡的影响，故在叶背测量点1处产生较大误差。

总体而言，叶片电化学多场耦合仿真可以形象化地反映出实际电化学加工过程，且仿真结果与实验结果基本吻合。验证实验加工出的叶片试件如图14所示。

图14 加工出的叶片试件

4 结论

(1)采用该仿真模型，能得到整个电化学加工过程中阳极轮廓、极间温度分布、电解液流速分布和电解液压力分布的变化规律。

(2)由不同加工电压对加工过程的影响的仿真得出，加工电压越大，极间温度分布越不均匀，从而使法向平衡间隙分布也越不均匀。

(3)由不同进液流量对加工过程的影响的仿真得出，法向平衡间隙沿流程方向逐渐增大， 且随着进液流量的增大，法向间隙逐渐减小。

(4)通过实验与理论仿真模型的比较，证明了仿真模型的有效性。

[1] 朱栋，朱荻，徐正扬.航空发动机叶片电解加工阴极数字化修正模型及其试验研究[J].机械工程学报，2011，47(7)：191-198. Zhu Dong，Zhu Di，Xu Zhengyang.Experimental Study on the Cathode Digital Modification of Turbine Blade in Electrochemical Machining[J].Journal of Mechanical Engineering，2011，47(7)：191-198.

[2] Klockea F，Zeisa M，Harsta S，et al.Modeling and Simulation of the Electrochemical Machining (ECM) Material Removal Process for the Manufacture of Aero Engine Components[J].Procedia CIRP,2013(6):265-270.

[3] Mount A R，Clifton D，Hpwarth P，et al. An Integrated Strategy for Materials Characterization and Process Simulation in Electrochemical Machining[J].Journal of Materials Processing Technology，2003，138(1)：449-454.

[4] 王福元，徐家文，赵建社，等.基于加工过程数值模拟的电解加工参数选择方法[J].中国机械工程，2006，17(7)：716-723. Wang Fuyuan，Xu Jiawen，Zhao Jianshe，et al.A Method of Selecting Electrochemical Machining Parameters Based on Numerical Simulation of Electrochemical Machining Process[J].China Mechanical Engineering，2006，17(7)：716-723.

[5] 李志永，朱荻，孙春华，等.发动机叶片电解加工阴极设计有限元数值解法研究[J].中国机械工程，2004，15(13)：1151-1154. Li Zhiyong，Zhu Di，Sun Chunhua，et al.Study on Finite-element Arithmetic in Electrochemical Machining for Turbine Blades[J].China Mechanical Engineering，2004，15(13)：1151-1154.

[6] 王峰，赵建社，江琴，等.基于电场仿真的微尺度群缝电解加工技术研究[J].中国机械工程，2013，24(23)：3154-3158. Wang Feng，Zhao Jianshe，Jiang Qin，et al.Investigation on Meso Scale Multi-groove Machining by ECM Based on Electric Field Simulation[J].China Mechanical Engineering，2013，24(23)：3154-3158.

[7] Fang Xiaolong，Qu Ningsong，Zhang Yudong，et al.Effects of Pulsating Electrolyte Flow in Electrochemical Machining[J].Journal of Materials Processing Technology，2014，214(1)：36-43.

[8] Hinduja S，Kunieda M.Modelling of ECM and EDM Processes[J].CIRP Annals-Manufacturing Technology，2013，62(2)：775-797.

[9] 王明环，章巧芳，彭伟.螺旋孔电解加工多物理场耦合机理研究[J].南京航空航天大学学报，2014，46(5)：774-779. Wang Minghuan，Zhang Qiaofang，Peng Wei.Multiphysics Coupling of Electrochemical Machining for Spiral Hole[J].Journal of Nanjing University of Aeronautics & Astronautics，2014，46(5)：774-779.

[10] Deconinck D，van Damme S，Albu C，et al.Study of the Effects of Heat Removal on the Copying Accuracy of the Electrochemical Machining Process[J].Electrochimica Acta,2011,56(16)：5642-5649.

[11] Deconinck D, van Damme V, Deconinck J.A Temperature Dependent Multi-ion Model for Time Accurate Numerical Simulation of the Electrochemical Machining Process.Part I: Theoretical Basis[J].Electrochimica Acta，2012，60(8)：321-328.

[12] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京：清华大学出版社，2004.

[13] 胡源.复杂型面电解加工电解液压力调控研究[D].南京：南京航空航天大学，2014.

(编辑 陈 勇)

Multi-physics Coupling Simulation of ECM Processes for Compressor Blade

Chen Yuanlong Fang Ming Pei Di Chang Weijie

Hefei University of Technology,Hefei,230009

A temperature dependent multi-physics coupling model was developed to predict ECM process and shorten the period for modifying machining parameters. Based on COMSOL multiphysics software, ECM processes for compressor blades were simulated and influences of the applied potential and the inlet mass flow on the normal equilibrium gap were analyzed. The simulation results indicate that with the applied potential increasing, the gap is increasing and the distribution of gap is less and less uniformity. However, with the inlet mass flow increasing, the distribution of gap tends to uniformity. The ECM experiments were carried out according to a set of simulation parameters. Comparisons between simulation and experimental results indicate that the errors are small when the blade profile curvature changes slowly and the errors are relatively large, but variation trend of the gap is same when the blade profile curvature changes fast.

compressor blade; electrochemical machining(ECM); multi-physics; coupling simulation

2016-01-05

国家自然科学基金资助项目(51075111)；中央高校基本科研业务费专项资金资助项目(JZ2013HGCH0004，JZ2015HGQC0206)

TG662

10.3969/j.issn.1004-132X.2016.22.018

陈远龙，男，1964年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为特种加工工艺及装备。方 明，男，1990年生。合肥工业大学机械与汽车工程学院博士研究生。裴 迪，女，1991年生。合肥工业大学机械与汽车工程学院硕士研究生。常伟杰，男，1981年生。合肥工业大学机械与汽车工程学院讲师、博士。