“一带一路”视角下基于模糊证据推理的物流园区选址方法

周映筱，赵 鹏

(北京交通大学 交通运输学院，北京 100044)



“一带一路”视角下基于模糊证据推理的物流园区选址方法

周映筱，赵 鹏

(北京交通大学 交通运输学院，北京 100044)

基于模糊理论和证据推理理论提出了一种基于模糊证据推理的物流园区选址方法.该方法首先确定“一带一路”下物流园区选址的评价维度，然后采用专家评分的方式得到每个备选选址在不同维度上的模糊评分，接着采用模糊Dempster-Shafer规则将备选方案在不同维度上的得分进行集成，最后根据综合得分鉴别出最优的备选方案.本文提出的园区选址方法是证据推理理论在物流园区选址问题上的一种新的尝试，旨为企业界和相关政府主管部门进行“一带一路”物流园区选址决策提供新的支撑工具.

物流园区选址；证据推理理论；模糊集

高效的物流基础设施是我国“一带一路”战略顺利推进的重要保障和前提.但是由于我国位于“一带一路”沿线的省市很多处在欠发达的内陆和西部地区，所以物流园区建设水平相对落后.一些省市虽然已经建设了物流园区，但是由于规划时间较早，未能放到此战略背景下进行考虑，因此，科学合理地加强沿线省市物流园区的建设是保证“一带一路”战略顺利实施的必要条件.

鉴于选址工作在物流设施规划中的重要意义，学者们已经对物流设施的选址方法进行了大量的探讨.常用的选址方法可以分为4类，第1类是基于综合得分排序的方法，其中最具代表性的是层次分析

法[1-2]、模糊综合评价法[3-6]和TOPSIS法[7-10]等.该类方法一般应用于备选方案的择优问题，虽然具有能够充分利用专家智慧和经验、操作方便等优点，但是无法有效解决专家判断的主观偏误问题；第2类是基于优化理论的选址方法，包括重心法[11-12]、最短路径法[13-14]、Baumol-Wolfe模型[15]、双层规划法[16-17]和混合整数规划法[18-19].第3类是基于智能模型的方法，主要是基于神经网络和遗传算法的选址方法，典型的研究可参考文献[20-21].第2类和第3类方法无需预先确定备选方案，能够直接生成最优方案，但是需要非常细节的实际数据或充足的数据积累，这在现实问题中往往难以满足；第4类是组合选址方法，如文献[22-23]分别将AHP和Steiner树，AHP和目标规划进行了组合.组合模型拥有不同模型的优点，同时也具有各自模型的不足；除了以上4类主要方法外，还有一些其他的方法，但是每种方法文献量很少且不成体系，如文献[24-25]分别运用改进的DEA模型和鲁棒优化理论解决物流中心选址问题.

“一带一路”战略的推行赋予物流园区选址工作新的特点，其中选址工作的前瞻性、系统性和数据难以获取性是3个极其鲜明的特点，这意味着在此战略背景下的物流园区选址工作面临3个困难：①在进行物流园区选址时必须同时兼顾当前具体要素和未来战略两个方面；②战略的推行将在较长时间内对我国交通物流行业产生重要影响，从而使经济变量取值出现较大不确定性；③在战略推行初期，相关数据严重缺乏.现有模型无法胜任“一带一路”背景下的物流园区选址工作，必须研究新的选址方法.

鉴于“一带一路”背景下物流园区选址的特点和难点，本文作者将模糊理论和证据推理理论相结合提出了一种基于模糊证据推理理论的选址方法，确定了选址模型中的6个评价指标:政策环境、地缘因素、基础设施、土地可得性、自然环境和发展潜力.该方法着重考虑“一带一路”下物流园区选址的新要求，既是证据推理理论在物流选址领域的新尝试，也可为我国物流园区选址工作提供一种新工具.

1 理论框架

本文提出的物流园区选址方法综合运用了模糊理论、配对对比方法和证据推理理论，然后集成这3种理论得到基于模糊理论和证据推理理论的多目标决策方法，最后将该方法用于最优备选物流园区选址的评价.

1.1 模糊理论

在物流园区选址决策中人们难以找到一个定量化指标以精确地判断选址的优劣，因此本文借助模糊集合理论来解决这个问题.

模糊集的概念可以由精确集引申而来，特征函数(隶属度函数)是连接二者的纽带.特征函数的值可以用来判断某个元素是否存在于特定集合内.假设存在一个n重符合变量X={X1,X2,…,Xn}，其论域记为U={U1×U2×…×Un}，R(X1,X2,…,Xn)是U上的一个n元限制，则集合{X,U,R(X;u)}中元素的特征函数可记为μR:U1×U2×…×Un→{0,1}并由下式定义：

(1)

式(1)说明精确集元素的特征函数的取值只能为0或1两种可能，非常明确.

然而对于模糊集而言，各元素的特征函数值不仅仅取0或1，而可以取区间[0,1]的任何值.所以模糊集合定义为“隶属度可在集合[0,1]上连续取值的一类对象的集合”.模糊集的严格定义可以描述如下：假设一个精确集的论域为U={U1,…,Un}，记为U=∑iUi，注意此处的∑不是加法运算而是表示联(集合运算方法).记μi为Ui在论域U的一个模糊子集F中的特征函数，则模糊子集F可表示为

(2)

1.2 配对对比法

为了更加客观全面地评价备选选址，需要综合考虑多方面的因素、采用多个评价指标.但是每个评价指标的重要程度是不相同的，需要采用科学的方式为不同的评价指标分配权重,配对比较法是解决以上问题的有效手段.

假设一个备选选址的评价指标体系由m (本例中m=3) 个评价指标构成，记为{E1, E2, E3}.配对比较法的具体步骤可以描述为：

1)采用百分制构造配对比较表(此处数据只是一个示例,在实际操作中数据由专家讨论给出)，如表1所示.

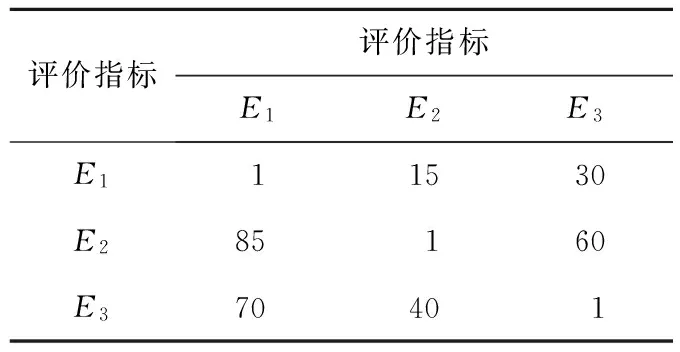
表1 配对比较表ⅠTab.1 Pairwise comparison table Ⅰ

相应地令

(3)

2)令cij=aij/aji(i≠j) 且cii=1，其中aij表示A中第i行第j列元素.令C=[cij],从而构造出中间配对比较矩阵C.

3)对配对比较矩阵C进行一致性检验.若C具有满意的一致性，则转到第4)步，否则请专家调整评价结果.

4)将C中同一列的第i行的数值除以第i+1(i=1,…,m-1)行的数值,计算值见表2.

表2 配对比较表ⅡTab.2 Pairwise comparison table Ⅱ

5)计算表2中每行的平均值.

(4)

(5)

6)令评价指标E3的平均相对重要性为1，记为mean(E3)=1，根据式(4)和式(5)可得到E1和E2相对重要性的计算公式.

7)将评价指标E1，E2和E3的平均相对重要性标准化,即得到最终的权重分配.

通过以上步骤，可以得到评价指标体系{E1,E2,E3}的权重分配.

1.3 证据推理理论

证据推理是通过D-S (Dempster-Shafer) 理论把多个观测或多个评价因素集成起来得到对事物的综合评价.D-S理论的一个重要概念是mass函数.mass函数m(x)的功能是将x的子集A映射为一个位于区间[0,1]上的实数，且满足以下性质：

m(φ)=0,m(A)≥0

(11)

∑A⊂xm(A)=1

(12)

其中φ表示空集.若x的子集A 满足m(A)>0则称A为函数m的焦元.设m1和m2表示x上的两个mass函数，A⊂x且A≠φ则m1和m2的直和可以定义为

(13)

式(13)称为D-S集成规则.式中:A是m1⊕m2的焦元;B和C分别表示m1和m2的焦元.式(13)意味着m1⊕m2的焦元可以通过对m1和m2的焦元做交运算得到，且(m1⊕m2)(φ)=0.

在证据推理理论中，可信度和似然度是两个非常重要的概念，也是衡量评价对象综合水平的重要统计量.可信度和似然度分别表示一个未知概率函数的下界和上界.模糊集上的可信度和似然度的计算公式可写为

Bl(B)=∑ainf(Aa⟹B)m(Aa)

(14)

Pl(B)=∑asup(B∧Aa)m(Aa)

(15)

式中:Aa表示第a个焦元；Aa⟹B表示Aa∨B;inf(Aa⟹B)表示Aa被B包含的程度;sup(B∧Aa)表示B和Aa相交的程度;sup和inf都是模糊运算符;表示运算符“非”.

1.4 基于模糊证据推理的多目标决策方法

将模糊理论、配对对比法和证据推理理论相结合，可以得到基于模糊理论和证据推理理论的多目标决策(多因素综合评价)方法，具体步骤描述如下：

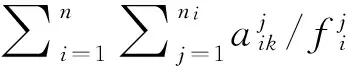
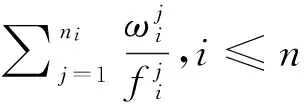
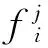
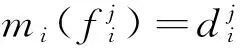
7)根据算式计算可信度和似然度

其中Aϑ是由所有mass函数的焦元相互组合而形成的集合中的第ϑ个元素.

8)计算似然度和可信度的和BPl=Bl(objj)+Pl(objj)，并以此作为最终的综合评价标准.

9)将待评价对象根据BPl的值按照从大到小的顺序排列，将排名最高的参评对象作为最优方案.

2 基于模糊集和证据推理的选址模型

本文选址模型考虑的因素包括政策环境、地缘因素、基础设施、土地可得性、自然环境和发展潜力等6个指标，依次记为S={Si，i=1,…,6}.假设每个评价指标的评级都是具有5个等级“非常好”、“好”、“一般”、“差”和“非常差”，记为A={Aj，j=1,…,5}.需要进行评价指标的配对分析、专家模糊评分、基于证据推理的综合评价，直到最终得到最优选址方案.

2.1 评价指标的配对分析

针对每个Si(i=1,…,6)，都可以建立一个5维配对对比矩阵H={Hpq，p,q=1,…,6}表示指标Si的评价级别对“当前选址是物流园区最佳选址”这条判断的支持力度.如对于指标S1，若H31=75而H13=25，则表示对于指标“环境政策”而言，“非常好”的政策环境对“当前选址是物流园区最佳选址”判断的支持力度是“一般”政策环境的3倍.

将配对对比得到的Si(i=1,…,6)的不同评级的权重向量记为

(18)

2.2 专家模糊评分

隶属度函数是模糊评分的重要基础，虽然学者们已提出多种隶属度函数形态，但是三角隶属度函数以期简单易行和计算复杂度小的特点得到了广泛的应用.三角隶属度函数数学表达式的一般形式为

(19)

式中:l、m、u分别是起点、最大值点和终点的横坐标值.

图1展示了多个不同评价等级Ri(i=1,…,4)的三角隶属度函数.

为了更加方便地表达三角隶属度函数，可以用隶属度函数3个顶点(起点、最大值点、终点)的横坐标数值的组合来表示该函数.如，评价等级Ri的三角隶属度函数可表示为(li,mi,ui)(i=1,…,4)，即第i个评价等级的起点、最大值点和终点横坐标的组合.

隶属度函数的确定要通过专家判断来进行，经常使用专家系统来保证判断结果的可靠性.本节采用了5级评判标准，所以最终得到的三角隶属度函数可记为{(li,mi,ui),i=1,…,4}.根据隶属度函数，专家可以针对备选选址A在每个评价指标上做出模糊评价，数学表达式为

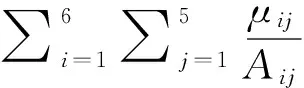
式中:Aij表示指标i的第j个评价等级；μij表示专家针对当前评价对象在Aij上的隶属度.

2.3 基于证据推理的综合评价

首先构造不同评价指标的评价等级的mass函数，令指标i的第j个评价等级的mass函数为

(20)

设mi的焦元集合为Fi={Aij,j≤5}，则所有焦元集合的笛卡尔积可记为F1⊗…⊗F6，数学表达式为

F1⊗…⊗F6=A1j1∧A2j2∧…∧A6j6

(21)

其中Aiji(ji=1,…,5)表示mi的焦元.

使用D-S规则将mass函数在F1⊗…⊗F6进行综合集成得到综合mass函数m=m1⊕…⊕m6.计算当前评价对象的可信度Bl和似然度Pl，并把可信度和似然度之和BPl作为评价当前选址的最终指标.计算所有对象的BPl值，然后选取BPl最大的备选选址作为最优选址.

3 数据模拟

本节使用数据模拟方法详细展示基于证据推理理论的宏观选址模型的具体操作过程和最终结果.

3.1 场景设定

假设有4个备选区域(省、市)，记为{objj,j=1,…,4}，任务是从这4个备选区域中选出最佳的选址方案来.评价指标及评价指标的等级定义与第2节相同.定义A={Aj，j=1,…,5}.Aij(i≤6，j≤5)表示第i个指标的第j个评价等级，如A21表示备选选址在“地缘因素”的评价等级是“好”.

使用专家系统对备选选址在每个指标上的表现进行评分，并经过专家讨论确定5等级隶属度函数.假设专家系统对备选选址的评分如表3所示，确定的隶属度函数记为{(0,0,0.3), (0.1,0.3,0.5), (0.3,0.5,0.7), (0.5,0.7,0.9), (0.7,1.0,1.0)}，如图2所示.

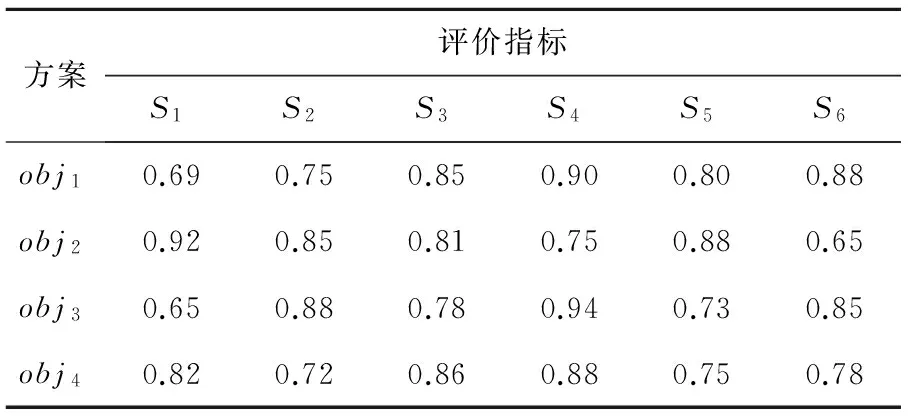
表3 备选选址得分Tab.3 Scores of candidate locations

将表3中的数据按照图2所示的隶属度函数进行计算，可以得到备选选址在每个评价指标不同等级上的隶属度函数.表4展示了4个备选选址方案在第1个指标上5个不同等级的隶属度，由于篇幅所限，其余指标的具体数值此处略.

表4 选址方案在每个评价指标不同等级上的隶属度Tab.4 Menbership values of candidate loctions regarding different evaluation criteria and degrees

使用专家系统对6个评价指标的5个不同评价等级的相对重要性进行评判.要指出的是，在6个评价指标中“政策环境”和“发展潜力”是对物流园区长期发展的考量，评价等级越高越好；“土地可得性”和“自然环境”是物流园区建立和运行的物质环境基础，只要适用即可，不需要追求最佳评级；“地缘因素”、“基础设施”是对当地物流当前状况的考量，这两个因素的评价等级越高意味着需要付出的成本也越高，因为当地的人工成本、地价等都会更高，因此这两个因素也是遵循适用性原则，不追求最高的评价等级.所以，本文设“政策环境”和“发展潜力”的评价等级重要性的配对对比矩阵相同(见表5)，而“土地可得性”、“自然环境”、“地缘因素”和“基础设施”共用一个等级重要性配对对比矩阵(见表6).

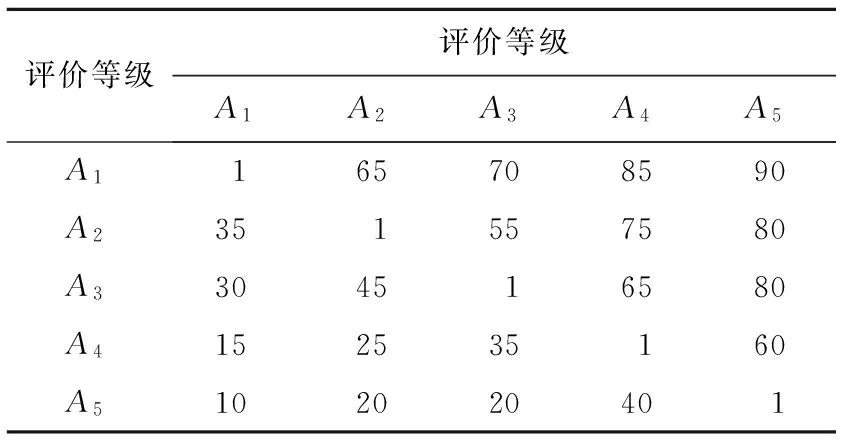
表5 政策环境和发展潜力的评价等级配对对比表ⅠTab.5 Pairwise comparison table Ⅰ of policy environment and development potential

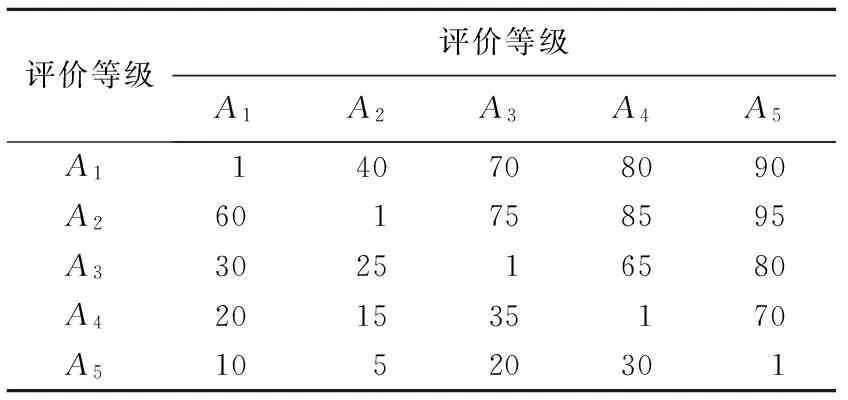
表6 其余4个指标的评价等级配对对比表ⅠTab.6 Pairwise comparison table Ⅰ of the remaining 4 criteria

3.2 基于配对对比法判定评价等级重要性

根据表5和表6中的数值求解不同评价等级的权重分配.

1)一致性检验

表7 政策环境和发展潜力的评价等级配对对比表ⅡTab.7 Pairwise comparison table Ⅱ of policy environment and development potential

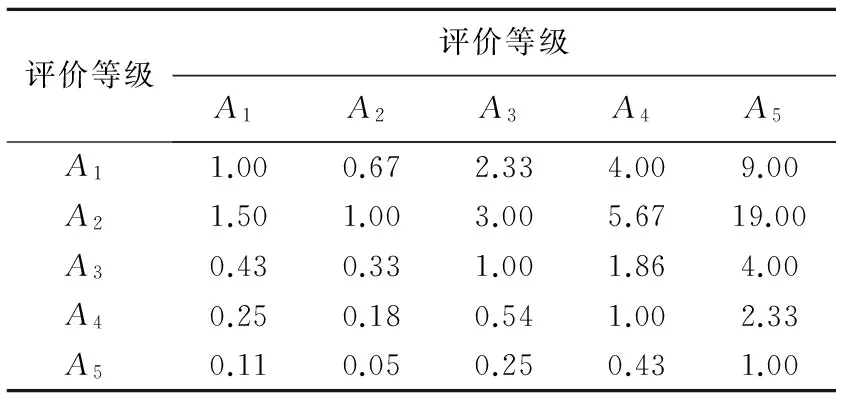
表8 其余4个指标的评价等级配对对比表ⅡTab.8 Pairwise comparison table Ⅱ of the remaining 4 criteria

令B为表7对应矩阵，C为表8对应矩阵.将B和C按列标准化，然后再按行相加并归一化，可分别得向量ωB=[0.45，0.23，0.19，0.08，0.05]T和ωC=[0.30，0.46，0.14，0.07，0.03]T，进而可求得B和C的最大特征值分别为

(22)

(23)

所以矩阵B和矩阵C的偏离一致性系数分别为

(24)

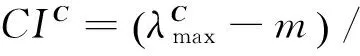
(25)

根据CIB、CIC，可求得矩阵B和矩阵C随机一致性系数为

IRB=CIB/RI=0.005/1.12<0.1

(26)

IRC=CIC/RI=0.005/1.12<0.1

(27)

所以矩阵B和矩阵C具有比较强的一致性.

2)判定评价等级权重

矩阵B和矩阵C具有较强的一致性，说明表7和表8中的数据可直接采纳，无需专家进行调整.根据前面的运算结果，对于“政策环境”和“发展潜力”两个因素，分配在评价等级“非常好”、“好”、“一般”、“差”和“非常差”上的权重为ω1=ωB=[0.45,0.23,0.19,0.08,0.05]，剩余4个因素的评价等级的权重分配为ω2=ωC=[0.30,0.46,0.14,0.07,0.03].

3.3 mass函数和焦元集合

根据表3中的隶属度矩阵可知，所有的备选选址在A14、A15、A23、A24、A25、A33、A34、A35、A44、A45、A53、A54、A55、A64和A65上的隶属度都为0，所以不同评价因素的焦元集合分别为F1={A11,A12,A13}, F2={A21,A22}，F3={A31,A32}, F4={A41,A42,A43}, F5={A51,A52}, F6={A61,A62,A63}，需要为Fi(i=1,…,6)中的元素定义mass函数.

令评价因素Si(i=1,…,6)的不同评价等级Aij(j=1,…,5)上的权重等于mass函数的值.根据ω1和ω2，可以定义如下mass函数：

记F=F1⊗…⊗F6,F为6个焦元集合的笛卡尔积得的新焦元.前3个焦元分别为：

F1=A11∧A21∧A31∧A41∧A51∧A61

(34)

F2=A11∧A21∧A31∧A41∧A51∧A62

(35)

F3=A11∧A21∧A31∧A41∧A51∧A63

(36)

使用D-S规则将mass函数mi(i=1,…,6)在F上进行集成得到集成mass函数m.

3.4 方案评价

根据表3，可以将F中的焦元表示为备选选址上的模糊集，如

(37)

用同样方法可求出所有F中焦元在备选选址上的模糊集.根据式(16)和式(17)，备选选址obji的可信度和似然度可写为

Bl(obji)=∑Fj[1-∨x≠objiμFj(x)]m(Fj)

(38)

Pl(obji)=∑FjFj{objj}m(Fj)

(39)

使用式(38)和式(39)得到4个备选选址的可信度Bl和似然度Pl，将其标准化之后4个备选选址的可信度和似然度组合分别为(Bl,Pl)1=(0.250,0.204)，(Bl,Pl)2=(0.247,0.188)，(Bl,Pl)3=(0.247,0.149)，(Bl,Pl)4=(0.257,0.459).4个备选选址的BPl=Bl+Pl的值分别为BPl1=0.454，BPl2=0.435，BPl3=0.396和BPl4=0.716.所以4个备选选址的优劣顺序为obj4>obj1>obj2>obj3，备选选址obj4是最优选址.

要特别指出的是，从表3中可以看出，obj4在“政策环境”和“发展潜力”两个指标上的综合表现与obj1相近，但是在其余的4个指标上的综合表现不及obj1.之所以obj4最终的评价结果优于obj1，是因为我们考虑到成本因素，从而在3.1节中的场景设定中做出了“好的选址应该在‘政策环境’和‘发展潜力’两个指标上尽可能地突出，而在其他4个指标遵循适宜原则不追求最高等级”的设定.数据模拟的结果表明:本文提出的方法能够把一些非常重要但难以量化的因素考虑进来，能够更加贴近现实应用.

4 结论

本文为了应对“一带一路”战略实施对我国物流园区选址带来的新挑战，综合应用模糊集理论和证据推理理论提出了一种基于模糊证据推理的选址方法,这是证据推理理论在物流园区选址领域的新尝试.数据模拟结果表明，该方法能够评选出合理的选址方案，并且可以将一些在实际选址决策中非常重要但难以量化的因素考虑进来，从而更加贴合实际.但是由于受数据可得性限制，本文只是采用模拟数据对方法进行了验证，方法的泛化性能和效果还需要在未来真实的选址工作中加以验证.

[1] CHANG P Y, LIN H Y. Manufacturing plant location selection in logistics network using analytic hierarchy process[J]. Journal of Industrial Engineering and Management, 2015, 8(5): 1547-1575.

[2] 周晓晔,王艳茹,刘作峰.物流中心选址的综合分析法研究[J].物流科技,2005,28(11):4-7. ZHOU Xiaoye, WANG Yanru, LIU Zuofeng. Research on the integrated analysis method of logistics center location[J]. Logistics Technology, 2005, 28(11): 4-7.(in Chinese)

[3] 李卓斌,綦群高,田童.基于模糊综合模型的商业地产多维定位研究[J].黑龙江农业科学,2013 (3): 44-46. LI Zhoubin, QI Qungao, TIAN Tong. Multidimensional location research based on the fuzzy comprehensive model of the commercial real estate[J]. Heilongjiang Agricultural Sciences, 2013 (3): 44-46.(in Chinese)

[4] LIN Q L, LIU H C, WANG D J, et al. Integrating systematic layout planning with fuzzy constraint theory to design and optimize the facility layout for operating theatre in hospitals[J]. Journal of Intelligent Manufacturing, 2015, 26(1): 87-95.

[5] LEE S K, MOGI G, HUI K S. A fuzzy analytic hierarchy process (AHP)/data envelopment analysis (DEA) hybrid model for efficiently allocating energy R&D resources:in the case of energy technologies against high oil prices[J]. Renewable and Sustainable Energy Reviews, 2013, 21: 347-355.

[6] KABIR G, SUMI R S. Power substation location selection using fuzzy analytic hierarchy process and PROMETHEE: A case study from Bangladesh[J]. Energy, 2014, 72: 717-730.

[7] ANAND G, KODALI R, DHANEKULA C S. An application of analytic network process for selection of a plant location: a case study[J]. International Journal of Services and Operations Management, 2012, 12(1): 35-66.

[8] NING X, LAM KC, LAM C K. A decision-making system for construction site layout planning[J]. Automation in Construction, 2011, 20(4): 459-473.

[9] LI Y, LIU X, CHEN Y. Selection of logistics center location using axiomatic fuzzy set and TOPSIS methodology in logistics management[J]. Expert Systems with Applications, 2011, 38(6): 7901-7908.

[10] 辛晶. 基于熵权TOPSIS 法的城市消防站选址模型[J].消防科学与技术,2010 (5): 25-27. XIN Jing. Optimization model of city fire station sites based on entropy weight TOPSIS[J]. Fire Science and Technology, 2010 (5): 25-27. (in Chinese)

[11] CHEN W. Location of logistics center planning of Changzhutan based on center-of-gravity method[C].Proceedings of the International Conference on Computer, Networks and Communication Engineering, 2013:703-705.

[12] 邓涛, 熊自明, 王青山. 一种结合重心法和 GIS 技术的机场抢修预置物资仓库选址模型[J]. 北京测绘, 2014 (5): 35-37. DENG Tao, XIONG Ziming, WANG Qingshan. A model for locating prestore material depot for airport rapid repair using barycentric model and the techonology of GIS[J]. Beijing Surveying and Mapping, 2014 (5): 35-37. (in Chinese)

[13] KLOSE A, DREXL A. Facility location models for distribution system design[J]. European Journal of Operational Research, 2005, 162(1): 4-29.

[14] BEASLEY J E. Lagrangean heuristics for location problems[J]. European Journal of Operational Research, 1993, 65(3): 383-399.

[15] 高学东, 李宗元. 物流中心选址模型及一种启发式算法[J]. 运筹与管理, 1994, 3(3): 56-62. GAO Xuedong, LI Zongyuan. Logistics center location models and a heuristic algorithm[J]. Operation and Management, 1994, 3(3): 56-62. (in Chinese)

[16] 鄢章华. 基于二层规划的物流中心选址模型研究[D]. 哈尔滨: 哈尔滨理工大学, 2008. YAN Zhanghua. Study on location model of logistics center based on bi-level programming[D]. Harbin: Harbin University of Science and Technology, 2008. (in Chinese)

[17] 李爽, 邓卫, 吕宜生. 基于场景规划的区域公共物流中心选址模型[J]. 交通运输系统工程与信息, 2009, 9(5): 85-89. LI Shuang, DENG Wei, LYU Yisheng. Location model of regional public logistics centers based on scenario planning[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(5): 85-89. (in Chinese)

[18] HAMACHER H W, LABBÉ M, NICKEL S, et al. Polyhedral properties of the uncapacitated multiple allocation hub location problem[R]. Kaiserslautern: ITWM, 2000.

[19] MAYER G, WAGNER B. HubLocator: an exact solution method for the multiple allocation hublocation problem[J]. Computers & Operations Research, 2002, 29(6): 715-739.

[20] SHAO Y, CHEN Q, WEI Z. Logistics distribution center location evaluation based on genetic algorithm and fuzzy neural network[M].Berlin :Springer,2009: 305-312.

[21] LIN J. The application of logistics center location based on fuzzy BP neural network[C]. Proceedings of 9th International Conference on the Service Systems and Service Management, 2012:264-267.

[22] 史占江. 物流配送中心选址及其应用研究[D]. 郑州: 河南大学, 2010. SHI Zhanjiang. Study on logistics distribution center location and application[D]. Zhengzhou: Henan University, 2010. (in Chinese)

[23] 莫海熙, 郜振华, 陈森发. 基于 AHP 和目标规划的物流配送中心选址模型[J]. 公路交通科技, 2007, 24(5): 150-153. MO Haixi, GAO Zhenhua, CHEN Senfa. Logistis distribution center location models based on AHP and programming[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 150-153. (in Chinese)

[24] 秦绪涛. 基于既有铁路货运站的铁路物流中心选址研究[D]. 北京: 北京交通大学, 2015. QIN Xutao. Study on railway logistics center location based on exisiting railway cargo transportation station[D]. Beijing: Bejing Jiaotong University, 2015. (in Chinese)

[25] 王保华,何世伟. 不确定环境下物流中心选址鲁棒优化模型及其算法[J]. 交通运输系统工程与信息, 2009,9(2): 69-74. WANG Baohua, HE Shiwei. Robust optimization model and algorithm for logistics center location and allocation under uncertain environment[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(2): 69-74.(in Chinese)

An approach to logistics park location based on fuzzy evidential reasoning from "One Belt and One Road" perspective

ZHOUYingxiao,ZHAOPeng

(School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044,China)

This paper proposes a new fuzzy evidential reasoning based logistics park location approach combined the fuzzy set and evidential reasoning theories. This approach first identifies the evaluation dimensions of a logistics park location from "One Belt and One Road" perspective.Then fuzzy scores of candidate locations in different dimentions are generated by experts. The fuzzy Dempster-Shafter rules are used to integrate the fuzzy scores in different dimensions to an aggregate value according the optimal location identified. The proposed approach is a new application of the evidential theory to locate the logistics park, and will provide a potential tool for decision makers of related enterprises and governmental departments.

logistics park location; evidential reasoning theory; fuzzy set

2016-09-15

国家自然科学基金重点资助项目(U1434207)

周映筱(1989—),女,山东淄博人,博士生.研究方向为物流管理.email:13114207@bjtu.edu.cn.

赵鹏(1967—),男,内蒙古通辽人,教授,博士,博士生导师.email:pzhao@bjtu.edu.cn.

F502

A

1673-0291(2016)05-0126-08

10.11860/j.issn.1673-0291.2016.05.022