复杂网络与软件度量分析

马 健 ，樊建平 ，刘 峰

(1.北京交通大学 计算机与信息技术学院，北京 100044;2.中国科学院 深圳先进技术研究院，广东 深圳 518055)



复杂网络与软件度量分析

马 健1，樊建平2，刘 峰1

(1.北京交通大学 计算机与信息技术学院，北京 100044;2.中国科学院 深圳先进技术研究院，广东 深圳 518055)

用复杂网络理论研究软件系统的复杂性，选取两款面向对象开源软件框架webwork和spring作为研究对象，无(有)向图节点代表类，边代表类间的依赖和关联等关系，将系统抽象为网络图，并对其拓扑结构进行分析.研究表明:无(有)网络具有较大的聚类系数和较小的平均路径长度，具有小世界特性.由于框架都使用了依赖注入和控制反转，程序中类之间的关系，完全由spring容器来控制，而不是由代码控制，容器运行时会根据spring提供的配置信息注入到组件中.用依赖注入的一个结果是改变了编译阶段部分类之间的相互关系,由原来的关联实体类到关联加载配置文件类 ,从而影响节点的度包括入度和出度，使无(有)向图的边(弧)数改变.实验结果表明：度分布统计特性仍然具有无标度特性.

软件度量；复杂网络；度分布；聚类系数

从20世纪70年代至今，软件系统已经变得极其复杂,“软件作坊”式的开发方式导致了软件危机的出现.1968年，NATO(北约)的科技委员会上第1次提出了软件工程(Software Engineering)这个概念.软件工程包括两方面的内容：软件开发技术和软件项目管理.要想有效管理，就难以绕开度量的问题[1-3].其中，软件度量是软件项目管理的一个关键环节，软件复杂性度量一直是软件工程的重要研究领域.软件复杂性是指理解和处理软件的难易程度，包括程序复杂性和文档复杂性，主要体现在程序复杂性中.复杂性度量方法有：代码行度量法(Loc)[4]，Mccabe圈复杂性度量法[5]，Halstead提出的程序体积度量[2].结构化程序软件复杂性的度量，出现了新的度量方法：Henry和Kafura提出的信息流度量[6]，Kavitha 和Shanmugam 提出的动态耦合测量[7]，Collofello提出的稳定度量[8].1990年以后，面向对象方法(Object-Oriented)逐渐成为软件设计和开发的主流，常用的度量方法包括：Chidamber和Kemerer提出了一系列面向对象度量方法也称C&K度量方法的面向对象度量[9]，Brito和Abreu提出了MOOD度量方法包含6个度量指标,是对面向对象的封装性、继承性、耦合性和多态性等方面提出的度量指标[10].

1998年Watts和Strogatz在Nature杂志上首次提出了“WS小世界”模型，提出的模型具有较大的聚类系数和较短的平均路径长度[11].1999年Barabási和Albert在的Science杂志上提出了无标度(BA)网络模型，以演员网络和WWW为例，考虑到增长特性和优先连接，指出现实中的网络节点在增加时优先与度数大的节点连接[12].2002年Valverde等从软件的源代码中提取组成单元抽象为节点，它们之间的依赖继承关系抽象为边，复杂的软件结构用软件图表示，研究结论表明:像大量人工网络那样，软件图也具有“小世界”和“无标度”的特性，为软件的度量引入了新的方法和工具[13].随后，Myers等在进一步将软件图中的无向边根据依赖(调用、继承和消息等)关系转化为有向边，得到了类似的结论[14].Vassa等提出边增长模型，检测面向对象系统结构的变化.发现在软件升级中，修改代码比删除代码更为常见，拥有更大扇入的类往往更容易被修改[15].

本文作者选取webwork 5.5和spring 4.2.0两款开源软件作为研究对象，框架都使用了依赖注入(Dependency Injection，DI)和控制反转(Inversion of Control ,IoC).不同于传统软件工程提供的方法仅仅关心局部特征，而是利用复杂网络理论从整体上把握系统，用复杂网络的方法度量软件.

1 复杂网络

1.1 无向图与有向图

1)一个无向图G定义为一个有序的二元组〈V,E〉 ，其中：V是非空有限集合称为顶点集，其元素称为顶点或节点；E称为边集，它是无序积V&V多重子集，其元素称为无向边，简称边.对于任意的v∈V ,称v作为G中边的端点的次数之和为v的度数，简称度[16].

2)有向图D与无向图的定义类似，只是边集E是卡氏积V×V的多重子集，其元素称为有向边，简称边.对于任意的v∈V，称v作为D中边的起始的次数之和为v的出度；称v作为D中边终点的次数之和为v的入度，出度与入度之和为v的度.

面向对象的软件系统可以表示成一个无向图G(V,E)或有向依赖图D(V,E)不同粒度的单元 (模块、包、类和方法)可以被视为节点n(其中,n∈V).这些单元的关系(调用、继承和消息等)形成图的边l(l∈E).

1.2 度与度分布

1)设vi是无向网络中的任意节点，与vi相关联的边的数量，称为该节点vi的度.若为有向网络，vi作为网络中边的终点的边的数量，称为vi的入度；vi作为网络中边的始点的边的数量，称为vi的出度.网络中所有节点vi的度ki的平均值称为网络的(节点)平均度，记为〈k〉[17]为

(1)

2)P(k)的含义是一个随机选定的节点的度恰好为k的概率.网络中节点的度的分布情况用分布函数P(k)来描述.

有向网络的平均度可以求平均入度〈kin〉和平均出度〈kout〉为

(2)

(3)

Pin(k) 和Pout(k)分别表示入度分布和出度分布，含义是一个随机选定的节点的入度或出度恰好为k的概率.

无标度网络具有幂指数形式的度分布，即p(k)～k-γ，有时也用累积度分布来描述度的分布情况，用公式表示为

度分布与累积度分布在双对数坐标中均表现为一条负斜率的直线.揭示网络的度分布的统计特性对于复杂网络研究具有重要意义，度描述了节点相互连接的统计特性，在社交网络中，度数越大的节点往往对应着明星用户，拥有更多的粉丝和网络影响力,也是复杂网络演化的重要性质.

1.3 聚类系数

1)无向网络中的节点vi与其他ki个节点相邻，在这ki个节点之间最多可能有ki(ki-1)/2 条边，而实际存在的边数Ei，两者之间的比值为

(4)

式中Ci为节点i的聚类系数.

假设网络的节点数为N，网络的聚类系数定义为

(5)

2)所有以有向网络中的节点vi为终点的弧的起始节点及它们之间的弧构成一个小集团，称之为入集团；而所有以该节点为起点的弧的终止节点及它们之间的弧构成一个小集团，称之为出集团[18].有ki,in个节点作为边的始点，与ki,in个节点最多可能有ki(ki-1)条边，而实际存在的边数Ei，定义Ci,in称节点vi的入集聚系数为

(6)

Ci,out称节点vi的出集聚系数为

(7)

Cin是网络的入集团的聚集系数为

(8)

Cout是网络的出集团的聚集系数为

(9)

1.4 平均路径长度

网络中两个节点vi,vj之间边数最少的一条简单路径，称为测地线.网络中两个节点i和j之间的距离dij定义为测地线的边数，网络的直径(diameter)，记为D定义为网络中任意两个节点之间的距离的最大值称为D=max dij.

网络的平均路径长度L定义为所有节点对之间的距离的平均值为

(10)

如不考虑节点到自身的距离，在式中包含了节点到自身的距离dii=0，网络的平均路径长度L为

(11)

有向网络中定义平均路径与无向网络非常类似，只是有向图路径中有向边方向必须一致[7-8]，网络的平均路径长度L为

(12)

复杂网络具有大的聚类系数和小的平均距离，具有小世界效应.

2 复杂性度量

本文作者使用两款开源软件对面向对象框架webwork和spring进行分析.使用DependencyFinder和Pajek作为分析工具.

webwork是由OpenSymphony组织开发的，致力于组件化和代码重用的J2EE Web框架.spring是轻量级的Java 开发框架,见表1.

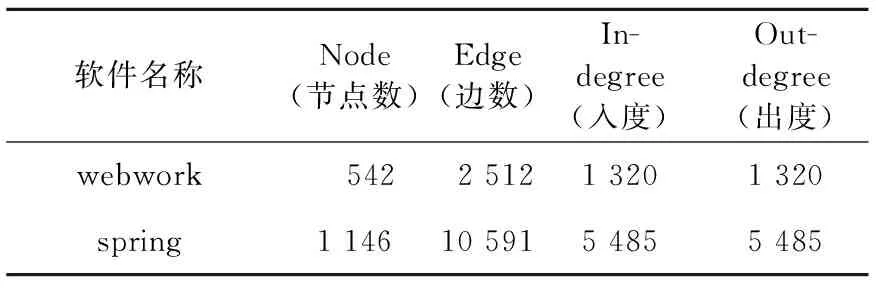
表1 两款软件的参数Tab.1 Parameters of the two software

DependencyFinder分析工具可以实现从Java字节码文件中抽取依赖关系和面向对象度量.Pajek是专门用来分析大型网络(含有成百上千个节点的专用程序)[19].

2.1 软件依赖

图1为模块(对象、类、方法和子程序)抽象为节点A、B、C，关系抽象为边.其中图1(a)为编写的一段示例代码，图1(b)表示类A,B,C之间的关系.图中的边表示类之间的无向关系.图(c)表示类A,B,C之间的有向关系.类B调用了A中的方法aMethod(·)，C调用了B中的方法bMethod(·).以便于对多线程序进行度量.

2.2 webwork和spring的参数分析

Pajek运行在Windows环境，用于带上千及至数百万个节点大型网络的分析和可视化操作[19].

图2是用Pajek画出的webwork包为节点的无向软件关系图.图3是spring包为节点的有向软件关系图.图2中点表示软件系统中的包，边(弧)表示包之间有依赖等关系.

2.3 webwork和spring的聚类系数

表2中为将webwork和spring抽象为无向网络和有向网络入集团和出集团时的聚类系数.

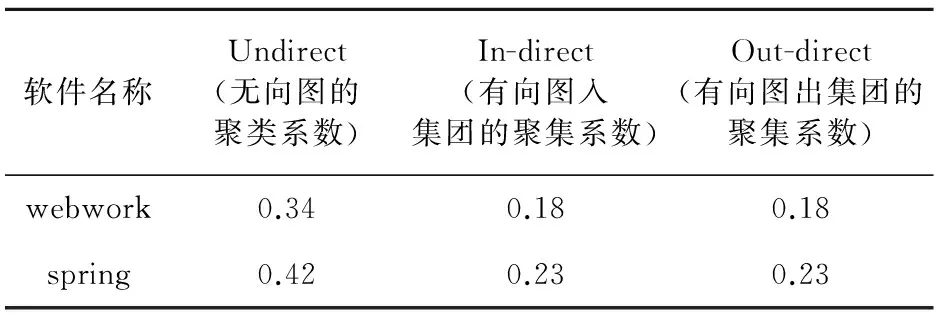
表2 两款软件的聚类系数Tab.2 Clustering coefficients of the two software

利用公式C=p=〈k〉/N,可计算出相同节点情况下随机网络的聚类系数，其中:C是聚类系数;p代表ER随机图两节点连接的概率;〈k〉为平均度;N为网络节点数.ER随机网络服从泊松分布，计算可得出：与webwork相同节点的随机网络的聚类系数分别为0.01，0.002，0.002，和spring相同节点的随机网络的聚类系数分别为0.017,0.004,0.004.对比表2中的数据可以看出软件复杂网络的聚类系数明显大于随机网络的聚类系数.软件复杂网络有明显的聚类特性.

2.4 webwork和spring的平均路径长度

表3中为将webwork和spring抽象为无向网络和有向网络入集团和出集团时的平均路径长度.

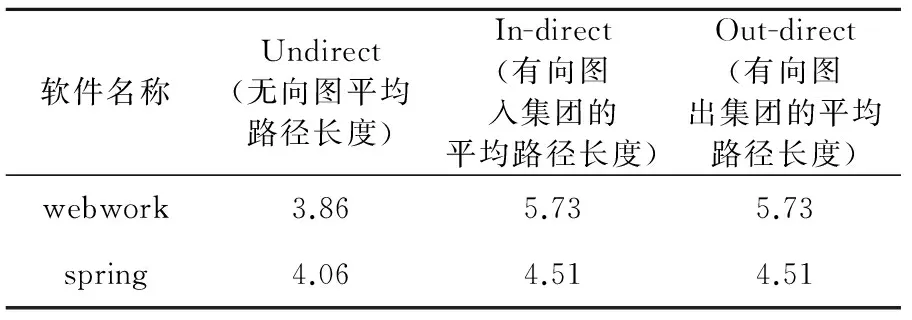
表3 两款软件的平均路径长度Tab.3 Average distances of the two software

利用公式L=ln N/ln〈k〉可计算出相同节点情况下随机网络的平均路径长度，其中，L为随机网络的平均路径长度，N为网络节点数，〈k〉为平均度，计算可得出：和webwork相同节点的随机网络的平均路径长度分别为2.82，7.07，7.07，和spring相同节点的随机网络的平均路径长度分别为2.68，5.35，5.35.对比表3中的数据可以看出，软件复杂网络的聚类系数明显接近于随机网络的平均路径长度聚类系数，软件复杂网络具有小世界特性.

2.5 webwork和spring的度分布

复杂网络的连接度分布服从幂律特征，即网络节点的度函数具有幂律形式，节点的连接没有明显的尺度特征，不像随机网络可以把平均度看作节点度的特征，这类网络也称作无标度网络.

图4和图5是无向图的度分布与有向图图的入度、出度的p(k)分布函数.而且曲线可以看出拟合成一条直线(以下图都用 “.”表示无向图;“*”表示有向图入度;“+”表示有向图出度).

图6和图7是无向图的累积度分布与有向图图的累积入度、出度的p(k)分布函数.而且曲线可以拟合成一条直线.

网络中节点出现了很多度数为某些较大值时，没有对应节点的度数等于该值，如果将对应的度数为零的值去掉去掉，图8和图9是简化的无向图的累积度分布与有向图图的累积入度、出度的p(k)分布函数.而且曲线可以拟合成一条直线.

通过分析网络的度分布和累积度分布表明：表明软件图具有幂律分布特性，也就是无标度特性.

3 结论

本文使用webwork和spring作为研究对象，其不同于其他软件的特点是原来的关联实体类到关联加载配置文件类 ,影响节点的度包括入度和出度，使无(有)向图的边数改变.本文采用逆向工程的方法，得出网络模型.使用复杂网络理论分析，复杂网络复杂性度量计算其聚类系数和平均路径长度，分析结果：同其他面向对象软件类似软件内部结构具有小世界特性.对其度分布进行分析，结果显示，网络节点的度函数具有幂律形式，具有无标度特性.

[1] 你如果无法度量它，就无法管理它[EB/OL].(2013-03-27)[2015-12-30]. https://book.douban.com/review/5823792/. It you can't measure it,you can't manage it[EB/OL].(2013-03-27)[2015-12-30].https://book.douban.com/review/5823792/. (in Chinese)

[2] EMERSON T J. A discriminate metric for module comprehension[C]. Proceedings of 7th International Conference on SW-Engineering , 1984: 294-431.

[3] MA Y HE K, DU D. A qualitative method for measuring the structural complexity of software systems based on complex networks[C]. Software Engineering Conference, 2005: 257-263.

[4] HALSTEAD M H. Elements of software science[M].New York: Elsevier North-Holland, 1997: 2-10.

[5] MCCABE T J. A complexity measure[J]. IEEE Transactions on Software Engineering, 1976,2(4):308-320.

[6] HENRY S M, KAFURA D. Software structure metrics based on information flow[J]. IEEE Transactions on Software Engineering, 1981,7(5): 510-518.

[7] KAVITHA A, SHANMUGAM A. Dynamic coupling measurement of object oriented software using trace events[C]. International Symposium on Applied Machine Intelligence and Informatics, 2008: 255-259.

[8] YAU S S , COLLOFELLO J S. Some stability measures for software maintenance[J]. IEEE Transactions on Software Engineering, 1980,6(6): 545-552.

[9] CHIDAMBER S R, KEMERER C F. A metrics suite for object oriented design[J]. IEEE Transactions on Software Engineering,1994, 20(6):476-492.

[10] BRITO F, ABREU E. MOOD-metrics for object-oriented design[C]. COOPSLA’94 Workshop on Pragmatic and Theoretical Directions in Object-Oriented Software Metrics,1994.

[11] WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393: 440-442.

[13] VALVERDE S, CANEHO R F, SOLE R V. Scale free networks from optimal design[J]. Europhysics Letters, 2002, 60(4):512-517.

[14] MYERS C R. Software systems as complex networks:structure,function,and evolvability of software collaboration graphs[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2003,68(4):352-375.

[15] VASA R,SCHNEIGER J G,WOODWARD C, et al. Detecting structural changes in object oriented software systems[C]. International Symposium on Empirical Software Engineering, 2005: 479-486.

[16] 耿素云，屈婉玲，王捍贫.离散数学教程[M].北京:北京大学出版社,2002:109-110. GENG Suyun, QU Wanling, WANG Hanpin.Discrete mathematics[M].Beijing:Peking University Press,2002:109-110.(in Chinese)

[17] 汪晓帆，李翔，陈关荣. 复杂网络理论及其应用[M]. 北京：清华大学出版社,2006：1-48. WANG Xiaofan，LI Xiang，CHEN Guanrong. Complex networks theory and its application [M]. Beijing: Tsinghua University Press, 2006:1-48.(in Chinese)

[18] 复杂网络基础理论[EB/OL].(2013-05-02)[2015-12-30] .http://wenku.baidu.com/link?url=UonUDDZwfQoffb VwSju8YrMsOuEB-sHcmdOtbRJN2O ZGPT Jw- LQyEN4vz8b2o9Po7d2hXQRTeu EonnshKEn-B-Sb B-TWxQeceDi0v0w3aVeda. Complex network fundemental theory[EB/OL].(2013-05-02)[2015-12-30] .http://wenku.baidu.com/link?url=UonUDDZwfQoffb VwSju8YrMsOuEB-sHcmdOtbRJN2OZGPT JwLQyEN4vz8b2o9Po7d2hXQRT-eu EonnshKEn-B-Sb BTWxQeceDi0v0w3aVeda.(in Chinese)

[19] Pajek中文使用手册[EB/OL].(2012-05-19)[ 2015-12-30]. http://www.doc88.com/p-395360089504.html. Pajek User manual in Chinese[EB/OL].(2012-05-19)[ 2015-12-30]. http://www.doc88.com/p-395360089- 504.html. (in Chinese)

Complex networks and software metrics analysis

MAJian1，FANJianping2，LIUFeng1

(1.School of Computer and Information Technology , Beijing Jiaotong University, Beijing 100044，China ; 2. Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences， Shenzhen Guangdong 518055， China)

Complex network theory is used to study the complexity of the software system in this paper. The selected object-oriented open-source software framework both webwork and spring as the research object, undirected (directed) graph nodes representing classes, relationships between classes edges representing dependency, association, etc., the system is abstracted to the network graph and its topology is analyzed. Studies show that undirected (directed) network has a large clustering coefficient and a smaller average path length, which are characteristics of a small world. Because of the inversion control and dependency injection used in the framework, program relations between classes, entirely controlled by the spring container, rather than by code control, will be injected into the container runtime according to configuration information provided by the spring assembly. Using dependency injection is to change the relationship between the compilation phases of the class such as an associated entity class changed to the class of associated load configuration file. Thus it influences the degree of the nodes including in-degree and out-degree and change the number of undirected (directed) graph edges (arcs) has been changed. The results show that the statistical properties of the degree distribution still have scale-free characteristics.

software metrics; complex network; degree distribution; clustering coefficients

2016-02-21

国家“863”高技术研究发展计划项目资助 (2015AA043701)

马健(1985—)，女，山西长治人，博士生.研究方向为轨道信息交通技术.email:13112083@bjtu.edu.cn.

TP311

A

1673-0291(2016)05-0023-06

10.11860/j.issn.1673-0291.2016.05.004