莱斯信道下大规模MIMO系统上行资源分配研究

陶 成, 李亚鹏,刘 留，李泳志

(1.北京交通大学 电子信息工程学院，北京 100044；2.东南大学 移动通信国家重点实验室，南京 211198)



莱斯信道下大规模MIMO系统上行资源分配研究

陶 成1,2, 李亚鹏1,刘 留1,2，李泳志1

(1.北京交通大学 电子信息工程学院，北京 100044；2.东南大学 移动通信国家重点实验室，南京 211198)

考虑了莱斯信道下单个小区上行多用户大规模MIMO系统，对上行链路的资源分配进行了研究.假设基站通过上行训练序列来估计信道，分别采用最大比合并接收和迫零接收来对信号进行接收.通过联合选择训练序列长度、训练序列功率和发送的数据功率来优化小区在相干时间内固定能耗下的频谱效率.仿真结果表明：经过优化系统的频谱效率有所提高，莱斯因子K越小，优化效果越明显，导频的功率越大；反之优化效果不明显，导频的功率越小.

大规模MIMO系统；莱斯信道；资源分配；频谱效率

近年来，大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)系统受到广泛关注[1-3],在该系统中，上百根的基站天线在同一时频资源块上同时服务数十个单天线用户.该系统不仅具备了多用户MIMO系统的优点，而且有着通过使用简单的线性接收机来消除噪声、减少能耗和增加频谱效率的潜力[3]，因此成为第5代移动通信系统的关键技术之一.对于大规模天线技术的性能分析和研究进展很快，文献[4]研究了大规模多天线无线信道的特点和无线信道的信道容量.文献[5]研究了莱斯信道下单小区大规模MIMO系统上行链路的可达速率性能.文献[6]研究了瑞利信道下单小区大规模MIMO系统的频谱效率和能量效率.文献[7]研究了多小区大规模MIMO系统存在导频污染和采用信道估计下的可达速率等性能.但是这些分析都是假设导频和数据的每个符号的功率都是相等的，然而这种功率平均分配的策略在功率较小时会引起“平方效应”[6].这是因为当功率较低时，导频功率和数据功率同时降低，而信道容量近似正比于导频功率的平方，从而衰减很大，降低了系统的能量效率.

随着无线通信高速率需求的不断增加，无线通信设备的能耗也急剧增加，如何优化能效受到了广泛的关注.文献[8]给出了上行链路多用户大规模MIMO系统中一种接近最优的能效优化迭代算法.文献[9]研究了瑞利信道下多小区大规模MIMO系统通过优化导频长度、导频功率和数据功率来提高能量效率.文献[10]研究了瑞利信道下单小区上行链路大规模MIMO系统，通过控制不同用户的功率分配和导频与数据功率的分配来提高能效，整个过程也是在瑞利信道模型下进行的，然而瑞利信道模型只能代表一类特殊的信道模型，忽略了在发射机和接收机之间存在直射径或者反射径的情况，因此需要考虑更复杂的信道模型来研究功率分配对于能量效率的改善情况.

本文作者考虑单小区大规模MIMO系统的上行链路.假设用户与基站间的信道为莱斯信道，且基站接收端分别采用最大比合并接收机和迫零接收机来接收信号.首先对两种接收机下的频谱效率表达式进行了泰勒展开，发现在莱斯信道下的实际系统中，即发射导频和数据功率相等的情况下,当信道具有强直射径时，系统总的频谱效率没有“平方效应”，而当信道的直射径很弱时，系统总的频谱效率与瑞利信道类似，存在“平方效应”.然后对频谱效率的表达式为凹函数进行了证明，证实了可以通过资源分配来优化固定能耗下的频谱效率.

1 大规模MIMO系统模型

考虑典型的上行链路单个小区大规模MIMO系统.基站配置M根发射天线，小区内随机分布N个配有单天线的用户，并且满足M≫N.由于系统是单个小区模型，因此不存在其他小区的干扰.

1.1 信道模型

在信道估计阶段，基站通过用户发送的导频来进行信道估计.假设给每个用户分配长度为τ个符号的正交导频序列(N≤τ≤T),其中T是相干时间，用gmn=[G]mn来表示第n个用户和第m根基站天线之间的信道参数，它包括独立的快衰落、路径损耗和对数正态阴影衰落，可以表示为

(1)

式中：hmn表示第n个用户和第m根基站天线之间的快衰落参数；βn代表第n个用户包括路径损耗和对数正态阴影衰落的大尺度衰落参数，并假设它对于基站天线阵列是恒定的.因此总的信道参数可以表示为

G=HD1/2

(2)

其中：[H]mn=hmn，[D]nn=βnn.快衰落参数矩阵包含两部分：代表直射径的确定参数和代表散射径的瑞利分布参数.莱斯因子K代表直射径和散射径的功率之比，假设第n个用户的K因子为Kn，快衰落参数矩阵H表示为[5]

(3)

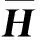
(4)

式中：d代表基站天线间距；λ代表波长；θn代表第n个用户的到达角.本文假设d=λ/2.

1.2 发送和接收

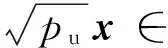
(5)

式中，n∈M×1是均值为0，方差为1的复高斯白噪声向量.用表示信道估计误差，表示线性接收矩阵.则接收的符号向量经过线性处理后为

(6)

因此估计到的第n个用户信号可以表示为

(7)

1.3 系统频谱效率

以系统的频谱效率作为能效优化的指标，本小节分别对采用最大比合并(MRC)接收机和迫零(ZF)接收机的系统性能进行分析.

1.3.1 最大比合并接收

(8)

式中，pu和pp分别为数据和导频的功率，ηn=τppβn/(1+τppβn)，an=βn(2MKn+2M2Kn)，bn=βn(M+M2)，

系统总的频谱效率为

(9)

接下来在两种情况下对比分析莱斯因子的大小是否影响频谱效率存在“平方效应”：一种是导频的发射功率固定，即导频功率与数据功率独立；另一种是实际系统的情况，即采用相同的发射功率来传输导频和数据.

当pu≪1，并且pp独立于pu时，将Smrc对pu进行泰勒级数展开得

(10)

其中

(11)

(12)

当pu≪1，并且pp=pu时，将Smrc对pu进行泰勒级数展开得

(13)

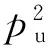
1.3.2 迫零接收

(14)

其中ηn=τppβn/(1+τppβn).系统总的频谱效率为

(15)

当pu≪1，并且pp独立于pu时，将Szf对pu进行泰勒级数展开得

(16)

当pu≪1 ，并且pp=pu时，将Szf对pu进行泰勒级数展开得

(17)

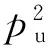
(18)

从比特能量的定义式可以看出，当pp=pu时，η=pu/S，从式(13)和式(17)可以看出，当数据功率足够小且直射径较强时，比特能量不会随着数据功率减小(频谱效率减小)而增大，最小的比特能量在最小的频谱效率处取得，因此在强直射径的莱斯信道模型下不存在像瑞利信道模型下的能效降低的情形.而pp≠pu时，在给定的能耗下，可以通过调整训练序列和数据的功率分配来提高系统的频谱效率，从而降低了比特能量，达到优化能效的目的.

2 能效资源分配

能效优化的基本思想就是通过调整发送数据的功率、导频功率及导频长度3个因素来提高系统的频谱效率.假设在相干时间T内发送能量的上限为P，则有

τpp+(T-τ)pu≤P

(19)

从式(19)可以看出，给定相干时间T和能量上限P，则存在最优的导频长度τ、导频功率pp和数据功率pu来最大化系统的频谱效率S，可以写成[9]

(20)

并且文献[9]证明了当导频长度τ=N时是最优的，因此式(20)可以写成

(21)

接下来只要证明式(9)和式(15)是凹函数就可以实现式(21)的优化，但是通过Mathematica求式(9)和式(15)对于pu的二阶偏导数结果十分复杂，很难证明它们是凹函数.而当pu≪1时，式(9)和式(10)是近似相等的，式(15)和式(16)是近似相等的，因此可以通过证明式(10)和式(16)入手.

引理 当pu满足0≤pu≤P/(T-N)时，对于MRC接收机和ZF接收机，式(10)和式(16)中系统总的频谱效率对于数据发送功率pu都是凹函数.

证明：

1)式(10)为凹函数：

要证式(10)为凹函数，首先进行换元，令pu=x·P/(T-N)，pp=(1-x)·P/N，其中x满足0≤x≤1，得到Smrc关于x的表达式记为f1(x).通过Mathematica 对f1(x)求二阶导数f1″(x)，再经过一些变换和运算能够得到 f1″(x)<0, 因此式(10)为凹函数.

2)式(16)为凹函数：

同样先换元，令pu=x·P/(T-N)，pp=(1-x)·P/N，其中x满足0≤x≤1，得到Szf关于x的表达式记为f2(x).用Matlab对f2(x)求二阶导数f2″(x)，直接观察得到f2″(x)<0, 因此式(16)为凹函数.

因此引理得证.

3 仿真结果与分析

本文采用Matlab的fmincon函数来解决式(21)的优化问题并且探究不同的因素对优化结果的影响.仿真采用一个半径为 rc=1 000 m的六边形小区，小区内随机分布着10个用户(N=10)并且每个用户离中心基站的距离不小于βn=zn/(rn/rh)vrh=200 m.相干时间为1 ms，相干带宽为200 kHz，对应的T=200个符号.采用大尺度衰落模型，其中衰落因子v=3.8，rn是第n个用户与基站的距离，zn是均值为0，标准差为σ=8 dB的对数正态随机分布.

图1探究优化前后系统总的信道容量随莱斯因子K的变化情况.仿真采用2 000个随机场景，求平均信道容量得到的结果，其中pu=10 dB，基站天线数M=100，莱斯因子K从-30 dB到30 dB递增.

从图1可以看出：1)对于MRC接收机，莱斯因子K为-30 dB时，优化后的和速率比优化前增加了1.37 (bits/s)/Hz；而莱斯因子K为30 dB时，优化后的和速率比优化前增加0.27 (bits/s)/Hz.2)对于ZF接收机，莱斯因子K为-30 dB时，优化后的和速率比优化前增加了4.099 (bits/s)/Hz；而莱斯因子K为30 dB时，优化后的和速率比优化前增加了0.52 (bits/s/)Hz.整体的优化效果是很明显的，提高了系统的频谱效率.但是在莱斯因子K变大的过程中，优化的效果是下降的，造成这种现象的原因是莱斯信道的信道模型存在一条已知的直射径，基站端要估计信道的散射径，当K因子很小时，散射分量所占比例很大，因此通过资源分配来提高对散射径信道估计的准确性使系统的信道容量有很大提升；而当K因子很大时，散射分量所占比例很小，因此通过资源分配来提高散射径信道估计准确性而获得的增益也就很小.

图2探究了最大比合并接收机和迫零接收机在不同的莱斯因子下优化后的资源分配比例.平均发射功率P=10T dB, 基站天线数M=100，莱斯因子K从-30 dB到30 dB递增.

从图2中可以看出：1)当莱斯因子K很小时(接近瑞利信道),pp/pu很大，例如当K=-30 dB时，MRC接收机导频功率是数据功率的6.45倍，ZF接收机导频功率是数据功率的13.34倍，此时在散射径的模型下，系统分配给导频更多的功率来更加精确的估计信道，从而提高系统总的频谱效率.2)当莱斯因子K很大时，pp/pu很小，例如当K=10 dB时，MRC接收机下系统的导频功率是数据功率的0.98倍，ZF接收机下系统的导频功率是数据功率的1.70倍，此时在有一条直射径为主导的莱斯信道模型下，MRC接收机和ZF接收机下系统的导频功率所占比例大幅度下降.3)当莱斯因子继续增加时，两种接收机下系统的导频功率都会小于数据功率，系统分配给数据更多的功率来提高直射径所占信道容量的比例，从而提高系统总的频谱效率.

图3是在1个用户随机分布下最大比合并接收机和迫零接收机在优化前后的和速率随着比特能量的变化情况.

选择莱斯因子K=-10 dB和K=10 dB，其中平均发射功率P=10 dB，基站天线数M=100.从图3中可以看出：1)当K=-10 dB时，直射径所占的比例很小，系统的信道模型接近瑞利信道模型，能够看到对于这两种接收机，比特能量都是在频谱效率为非0值的情况下取得最小值，在这个值以下，比特能量随着频谱效率的减少而增加，而在这个值以上，比特能量随着频谱效率的增加而增加.因此在比特能量较低时，对于给定的比特能量，存在两个频谱效率，考虑能效的情况下，应该避免较低的频谱效率，也就是信号的发射功率不应该太小，而且通过优化，在两种接收机下系统的能量效率都有所提高.而在比特能量较高时，平方效应消失了，但是系统的优化效果也明显降低.2)当K=10 dB时，对于这两种接收机，比特能量都是在频谱效率非常接近于0的情况下取得最小值，平方效应消失了，因此对于给定的比特能量，只需要选择对应的频谱效率和发射功率.另外两种接收机下系统的比特能量的优化并不明显.由此可知，图3得出的结论和1.3节的理论分析很吻合.

4 结语

1)针对莱斯信道下单个小区上行多用户大规模多输入多输出(MIMO)系统，对上行链路资源分配的能效优化进行了研究.基站通过上行的训练序列来估计信道，分别采用最大比合并接收和迫零接收来处理用户发送的信号，通过联合的选择训练序列长度、训练序列功率和发送的数据功率来优化小区在相干时间内固定能耗预算下的频谱效率.研究发现，实际系统中在直射径较弱时，信道模型接近瑞利信道，系统的频谱效率存在“平方效应”;而直射径较强时，系统的频谱效率不存在“平方效应”.

2)仿真结果表明：经过优化，两种接收机下系统的频谱效率都有所提高.但是对于不同的莱斯因子，系统的优化效果是不同的：莱斯因子K越小，系统的优化效果越明显；反之优化效果不明显.莱斯因子K越小，系统分配给导频的功率越大；反之系统分配给导频的功率越小.

[1] LARSSON E, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems[J]. IEEE Communications Magazine, 2014, 52(2): 186-195.

[2] MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications, 2010, 9(11): 3590-3600.

[3] RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO:opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine , 2013, 30(1): 40-60.

[4] 刘留, 陶成, 卢艳萍,等. 大规模多天线无线信道及容量特性研究[J]. 北京交通大学学报, 2015, 39(2):69-79. LIU Liu, TAO Cheng, LU Yanping, et al. Research on the propagation condition and channel capacity for Massive MIMO[J]. Journal of Beijing Jiaotong University, 2015, 39(2):69-79. (in Chinese)

[5] ZHANG Q, SHI J, WONG K, et al. Power scaling of uplink massive MIMO systems with arbitrary-rank channel means[J].IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 966-981.

[6] NGO H Q, LARSSON E G, MARZETTA T L. Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications, 2013, 61(4): 1436-1449.

[7] HOYDIS J, TEN BRINK S， DEBBAH M. Massive MIMO in the UL/DL of cellular networks: How many antennas do we need[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 160-171.

[8] 胡莹, 冀保峰, 黄永明，等. 基于上行多用户大规模MIMO系统能效优化算法[J]. 通信学报, 2015, 36 (1): 68-74. HU Ying, JI Baofeng, HUANG Yongming, et al. Energy-efficient optimal algorithm based on uplink multi-user very large MIMO system [J]. Journal on Communications,2015 ,36 (1): 68-74. (in Chinese)

[9] NGO H Q, MATTHAIOU M, LARSSON E G. Massive MIMO with optimal power and training duration allocation [J]. IEEE Wireless Communications Letters, 2014, 3 (6): 605-608.

[10] CHENG H V, BJöRNSON E, LARSSON E G. Uplink pilot and data power control for single cell massive MIMO systems with MRC[J].Mathematics, 2015.

Research on uplink resource allocation in massive MIMO system over Rician fading channels

TAOCheng1,2，LIYapeng1，LIULiu1,2，LIYongzhi1

(1.School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044,China; 2.National Mobile Communications Research Laboratory, Southeast University, Nanjing 211189, China)

Considering the uplink of a single cell massive Multiple-Input Multiple-Output(MIMO) system, a resource allocation scheme is investigated over Rician fading channels. It is assumed that the base station first estimates the channel vita uplink pilots and then employs the maximum ratio combining and zero forcing processing to detect received signals. By jointly selecting the training duration, the training signal power and the data signal power, the system can approach the maximum spectral efficiency for a given total energy budget. Numerical results show that the performance can be improved significantly for small Rician K-factor but slightly for large Rician K-factor. Furthermore, with the optimal resource allocation scheme, the fraction of the total transmission energy that is devoted to the pilot training decreases with the increasing of Rician K-factor.

massive MIMO system; Rician fading channels; resource allocation; spectral efficiency

2016-04-15

国家自然科学基金面上项目资助(61471027); 东南大学移动通信国家重点实验室开放研究基金资助项目(2014D05);北京市自然科学基金资助项目(4152043)

陶成(1963—)，男，山西侯马人，教授，博士.研究方向为移动通信架构和无线信道测量与建模.email: chtao@bjtu.edu.cn.

TN929.5

A

1673-0291(2016)05-0050-06

10.11860/j.issn.1673-0291.2016.05.009