追寻既“通”且“融”的数学学习
许贻亮

【教学内容】北师大版五上第五单元“分数的意义”第63至64页。
【教学目标】
1. 进一步理解“一个整体”“平均分”的意义,初步了解“比1大的分数”,能从多种角度理解分数。
2. 在观察、思考、迁移、拓展等数学活动中,借助几何直观和生活事例,培养合情推理能力,积累数学活动经验,体会数形结合、变中不变的数学思想方法。
3. 增强数学与生活的联系,进一步树立学习数学的自信心。
【教学过程】
一、唤醒经验
思考:看到课题“分数的再认识”,有什么想法吗?(突出对“再认识”的思考:已认识什么?再认识什么)
【设计意图】“分数的再认识”一课是学生在三年级学习了“分数的初步认识”后对分数意义的再一次深入认识。要突出“再认识”,首先就要先明确“已认识了什么”。
二、多元建构
(一)认识“一个整体”
谈话(出示8个苹果):如果把它们装在一个袋子中,叫做1袋苹果;如果把它们放在一个盘子里,叫1盘苹果;如果把它们装在一个篮子中,叫1篮苹果。数学上常用一个“圆”把它们圈起来,表示它们是“一个整体”。(板书)
对比:同样是这个人,怎么所占的分数会不一样?
拓展:还可以把什么看作“一个整体”?
(二)平分100万的遗产
事例:老人的100万遗产要分给4个子女,怎么分公平?(平均分成4份,各取1份)
冲突:是这样分吗?(出示:把支票4等分的图片)使学生的认知产生冲突(这样分的话,支票就作废了)
思考:怎样平均分?(先把支票换成等价的人民币再平均分)
(三)还能平均分吗
出示:马小跳的图片。
冲突:还能往下平均分吗?引发学生产生第2次的认知冲突——一个人怎么能再往下分呢?
【设计意图】通过“平分100万的遗产”和“往下分马小跳”,以通俗的事例,引发学生的认知冲突。在交流中,逐渐地让学生明白其中的事理,感悟其中的分法——“先换再分”和“想象地分”,从而较好地突破已有数学认知经验所形成的局限性。
(四)分数的“接龙”
活动1:数轴上的分数接龙。
观察:这一小段用分数几分之几表示?
拓展:再多1份呢?可以是多少份?
活动2:面积模型中的分数接龙。(图1)
【设计意图】教学中,借助鲜活的生活事例及几何直观,让学生感受从“不平均分”到“平均分”,从“实际地分”到“想象地分”,从“1以内的分数”到“1以外的分数”等,立足于整个单元的教学内容,把多元的素材融为一体,合力从抽象的角度、度量的意义、除法的意义等方面建构起学生关于分数的数学认知结构。在冲突中变通、在类比中强化、在思考中深入,从而在“学会”中进一步达成“会学”。
三、应用拓展
感悟:在单位“1”的数量不确定的情况下,谁取出的多并不能确定。
猜想:要猜中“终极密码”的答案,最多猜几次就行?
课前,让学生进行热身游戏——猜“终极密码”,即先在纸上写在一个自然数(1~100之间),让学生猜一猜写的是几?根据学生猜测的答案,给出正确答案的范围,再继续猜,直到猜中为止。活动中,把学生每次猜的数字都板书在黑板上,并统计出到猜中时的次数。如,猜第一个数“37”共用了11次,猜第二个数“82”共用了8次。这时,回首课前的活动,让学生展开思考:“要猜中终级密码,最多猜几次呢?”让学生展开猜想:11次、20次、99次等。
验证:借助面积模型的不断二等分,体会最多8次的道理。
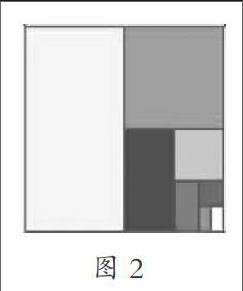
第一个数先猜是不是50(对半),这时就把1~100分成了两个“阵营”,要么答案在1~50之间,要么答案在50~100之间,两种情况必居其一,最多剩50种不同情况;接着再对半猜,如果答案在1~50之间,就猜是不是25,这时就又把1~50分成了两个“阵营”,要么答案在1~25之间,要么答案在25~50之间,两种情况必居其一,最多剩25种情况;再对半地猜,最多剩13种情况……以此类推。这时借助正方形的面积模型(图2),以“数形结合”的方式,帮助学生建立方法模型。
【设计意图】教学中,安排了2个层次的应用对比。从“不同分数的取”到“相同分数的取”,丰富学生关于“分数”的认知。刚开始是不同分数的取球,因为对应箱子也有大有小,拓宽学生表达的空间,在交流中增进学生数学理性思维的培养;接着便是不同对象的同一分数的捐款,学生便直通知识内核“不一定”,并说明理由。最后,在再认识“终极密码”数学游戏中,从“不确定次数”到“可确定次数”,把“数”与“形”有机地结合起来。
四、回顾升华
回顾:这节课,我们关于“分数”有了哪些新的认识?
感悟:你觉得“分数”怎么样?
【设计意图】通过回顾和感悟,一方面进一步把零散的知识串起来形成一个有机整体——核心是“把谁平均分”。另一方面,对以往的“平均分”做一次理性的认知和飞跃:从分实物到分数量,到“先换再分”,到“想象地分”,到线段上的平均分以及平面图形中的多次平均分。在回顾中进一步感悟知识,在交流对分数的感觉时,增强学生对数学学习的喜爱和学好数学的信心。
(作者单位:福建省晋江市第二实验小学 责任编辑:王彬)

