初中数学最短路径问题的探究与延伸

广西大学附属中学 芦英峰

初中数学最短路径问题的探究与延伸

广西大学附属中学 芦英峰

题目：（造桥选址问题）如图，A和B两地在一条河的两岸，现在要在河上造一座桥MN。桥造在何处可使从A到B的路径AMNB最短？(假定河的两岸是平行的直线，桥要与河垂直。）

一、审题分析

本题属于最短路径问题，学生比较陌生，对题目的理解难度比较大，首先引导学生通过多次读题理解题意：已知A、B两地在一条河的两岸，且河的两岸可以看成是平行的直线，则可画出两条平行的直线a和b，点A和点B是定点，分别位于两直线的两侧。现要建一座桥MN，要求桥与河垂直，即线段MN与直线a，b垂直。所要求的问题是桥造在何处可使从A到B的路径AMNB最短，即线段MN位于何处时，可使AM+MN+NB最小，从而将实际问题转化为数学问题，如图1所示。

图1

二、探究过程

1.探究线段MN的大致位置：学生在自主探究时，根据两点之间，线段最短，容易想到连接AB分别交直线a，b于M和N两点，则线段MN即为所求。如图2所示，引导学生思考这种作法是否可行，从而发现与题目中的条件“桥与河垂直”相矛盾。

图2

2.探究线段MN的准确位置。

引导学生复习前面学过的求直线上的点到直线外异侧两点的距离之和最小问题，已知A、B两个定点分别位于一条直线l的两侧，要在直线上找到一点使得它到这两个定点的距离之和最小，根据两点之间，线段最短，连接AB与直线l交于一点，即为所求。引导学生对比本题，思考能否通过某种途径将直线a和直线b重合在一起，从而将“两线两点”问题转化成“一线两点”问题，学生会想到利用平移的方法，从而得到作图思路。

作图步骤：（1）同时将直线a和点A沿与河岸垂直的方向平移一个河宽，使直线a与直线b重合，点A移动到A′。

（2）连接A′B交直线b于点N，过点N作MN⊥a，垂足为M，连接AM则线段MN即为所求。

（3）如图3所示。从而得到最短路径为：A→M→N→B

图3

3.证明线段MN的位置即为所求。

引导学生在直线b上异于点N任取一点G，过点G作GH⊥a，垂足为H，连接AH，GB，A′G，如图4所示，则只需证明AM+MN+NB＜AH+HG+GB。由于桥的长度不变，故MN=HG，从而只需证明AM+ NB＜AH+GB。根据平移性质可得AM=A′N，AH=A′G，进而将问题转化为只需证明A′N+NB＜A′G+GB。 由图可知，A′N+ NB=A′B，最终问题可转化为只需证明A′B＜A′G+GB。学生容易想到根据三角形的三边关系进行证明，最终得到证明思路。

图4

4.多种作图方法。

作法二：如图5所示，同时将直线b和点B沿与河岸垂直的方向平移一个河宽。使直线b与直线a重合，点B移动到B′，连接B′A交直线a于点M，过点M作MN⊥b，垂足为N，则线段MN即为所求。

图5

作法三：如图6所示，将点A沿与河岸垂直的方向平移一个河宽。点A移动到A′，连接A′B交直线b于点N，过点N作MN⊥a，垂足为M，连接AM，则线段MN即为所求。

点评：作法三与作法一本质上是相同的。

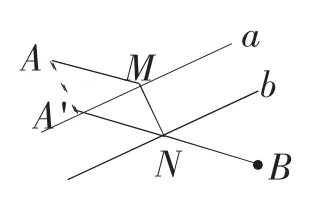
图6

作法归纳：

明确平移的目的是使两条直线重合在一起，从而将“两线两点”问题转化成“一线两点”问题，即转化成求直线上的点到直线异侧两点的距离之和最小的问题。从而得到一般作法：沿与河岸垂直的方向分别同时平移点A和直线a，点B和直线b到某个位置，使直线a和直线b重合，点A移动到A′，点B移动到B′，则同样也可以进行求解，留给学有余力的同学课后继续探究。

三、延伸推广

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。算法具体的形式包括：

1.确定起点的最短路径问题——即已知起始结点，求最短路径的问题。

2.确定终点的最短路径问题——与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。

3.确定起点和终点的最短路径问题——即已知起点和终点，求两结点之间的最短路径。

4.全局最短路径问题——求图中所有的最短路径。