满秩分解与秩不等式

章朝庆

（泰州职业技术学院基础科学部，江苏泰州　225300）

满秩分解与秩不等式

章朝庆

（泰州职业技术学院基础科学部，江苏泰州225300）

矩阵的满秩分解是矩阵分解中一类特殊的分解，即若A∈Rmr×n，则A可分解为一个列满秩矩阵F与一个行满秩矩阵G的乘积。文章给出了矩阵满秩分解的一些特殊性质及其证明，并应用满秩分解证明了四个秩不等式。

秩分解；标准型；矩阵

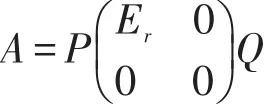
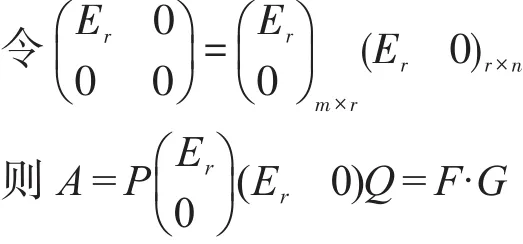
一般而言，一个矩阵的满秩分解并不是唯一的，但是不同的分解之间有定理2所述的关系:

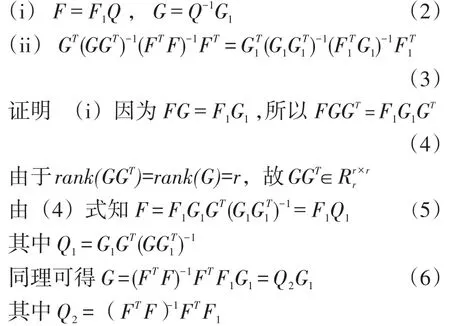
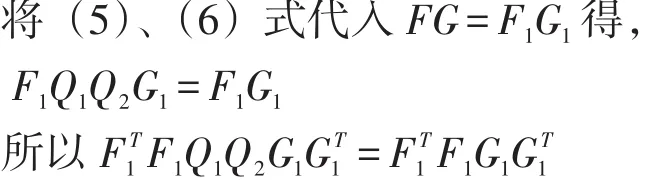
（ii）把（2）式代入GT(GGT)-1(FTF)-1FT，即得（3）式成立，证毕[1]。

同理可证，r=(BG)=r(B)，证毕。

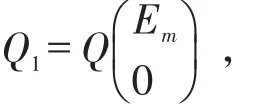
证明由定理4即可证得，证毕[2]。

应用满秩分解证明矩阵秩数方面的某些定理，有时比较简捷，现试用此种方法给出四个定理的证明。

因为AB=0，所以FGB=0

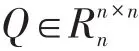
即r(A)+r(B)≤n，证毕。

证明先证右边结论成立

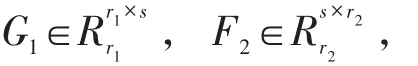
则r(AB)=r(F1G1F2G2)=R(G1F2)

由于G1F2∈Rr1×r2

所以r(G1F2)≤min(r1,r2)

即r(AB)≤min(r1,r2)

再证左边结论成立

因为r(AB)=r(G1F2)

令Q1P2D,D∈Rss×s

所以r(Dr1×r2)≥s-(s-r1)-(s-r2)=r1+r2-s

即r(AB)=r(G1F2)=r(Dr1×r2)≥r1+r2-s，证毕。

定理8r(ABC)≥r(AB)+r(BC)-r(B)

则r(ABC)=r((AF)(GC))≥r(AB)+r(BC)-r =r(AFG)+r(FGC)-r=r(AB)+r(BC)-r(B).证毕。

定理9r(A+B)≤r(A)+r(B)，r(A-B)≥r(A)-r(B)

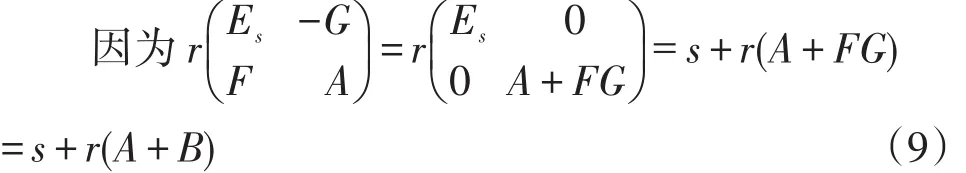
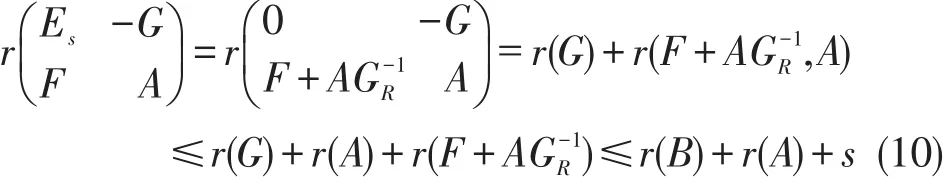
比较（9）、（10）式，得r(A+B)≤r(A)+r(B)+s

即r(A+B)≤r(A)+r(B)

由r(A)=r(A-B+B)≤r(A-B)+r(B)

得r(A-B)≥r(A)-r(B)证毕[3].

[1]房月华，陈萍.矩阵满秩分解及其方法[J].衡水学院学报，2011（4）：16-18.

[2]陈大新.矩阵理论[M].上海：上海交通大学出版社，1996.

[3]毛纲源.线性代数解题方法和技巧[M].长沙：湖南大学出版社，1987.

（责任编辑刘红）

Rank Decomposition and Inequalities of the Rank

ZHANG Chao-qing

(Taizhou Polytechnic College,Taizhou Jiangsu 225300,China)

The Full Rank Decomposition of the Matrix is a special kind of decomposition.If A can be decom⁃posed into the product of a Column Full Rank Matrix(F)and a Row Full Rank Matrix(G).The paper provides analysis and proof of special properties of the Full Rank Decomposition of the Matrix,and proves four inequali⁃ties with th件报告系统的填报内容设计件报告系统的填报内容设计e Full Rank Decomposition.

rank decomposition;standard form;matrix

O151.2

A

1671-0142（2016）02-0048-02

章朝庆（1957-），女，江苏如东人，副教授.