转化与化归的思想方法在立体几何中的应用
曹 静
(云南省昆明市官渡区第一中学 云南昆明 650200)
转化与化归的思想方法在立体几何中的应用
曹 静
(云南省昆明市官渡区第一中学 云南昆明 650200)
化归与转化的思想是指在解决问题时,采用某种手段使之转化,进而使问题得到解决的一种解题策略。化归与转化思想的核心是把生题转化为熟题,解题的过程就是一个缩小已知与求解的差异的过程,是未知向熟知转化的过程,因此每解一道题无论是难题还是易题,都离不开化归,本文从以下几个方面来阐述。
转化与化归思想 方法 应用
一、正与反的转化
解数学问题,一般总是从正面入手思考,但有时遇到从正面入手不易解决的情况,这时作逆向思考颇能奏效,这就是我们常说的“正难则反”的转化思想。
例1:设A、B、C、D是空间四点,且﹤ABC=﹤BCD=﹤CDA=﹤DAB=90°,求证:A、B、C、D在同一个平面上。
反证法:假设A、B、C、D不在同一平面上,则直线AB与CD是异面直线,∵﹤ABC=﹤BCD=﹤CDA=﹤BAD=90°,∴BC与AD均为异面直线AB、CD的公垂线,这与两条异面直线公垂线的唯一性矛盾,故命题为真。
二、位置关系的转化与化归
例2:设矩形ABCD,E、F分别为AB、CD的中点,以E F为棱将矩形折成二面角A-EF-C1(如图1),求证:平面A B1E∥平面C1DF.
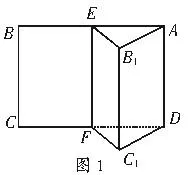
三、特殊与一般的转化
解数学题有许多一般规律,也有相当多的特殊技巧,在许多问题的研究中,常常需要从考察特殊情况入手,发现归纳出一般结论。在某些问题中,运用一些特殊的技巧往往能独辟蹊径,立见事半功倍之效,两者相辅相成,相得益彰。
例3:四面体ABCD四个面的重心分别为E、F、G、H,则四面体EFGH的表面积与四面体ABCD的表面积的比值是_______
解析:不妨设四面体ABCD为正四面体,棱长为1,由条件可知四面体EFGH也是正四面体,棱长为1/3,故它们表面积之比等于棱长之比的平方,即为1/9
四、空间向平面转化
例4:球面上有3个点,其中任意两点的球面距离都相等于大圆周长的,经3个点的小圆周长为4π,那么这个球的半径为( ).

分析:将空间的问题转化为平面的问题来处理,这是解题的通法
解:设A、B、C为球面上三点,过其中A、B两点的大圆,如图1,O为球心,则且OA=OB=R,
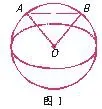
则AB=OA=OB=R
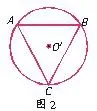
同理OC=OA=OB=R,OB=OC=BC=R,∴△A BC为等边三角形
设过A、B、C三点的小圆为⊙O′,如图2,半径为r,则由2πr=4π,得r=2,
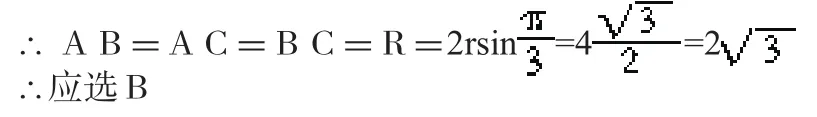
五、割补转化.
几何中的割补思想,通过分割与补形把不规则的几何体转化为常见的一些几何体进行求解。
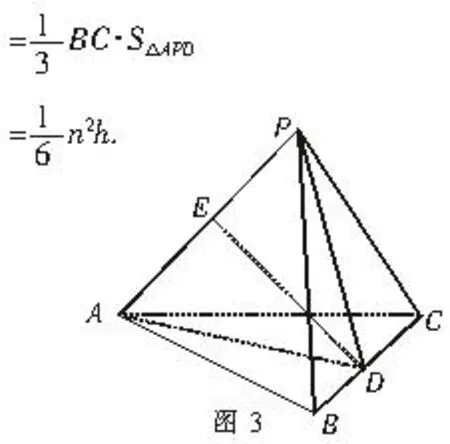
例5 :如图3,三棱锥P-ABC中,已知PA⊥BC,PA=BC=n,PA与BC的公垂线ED=h,求证:三棱锥P-ABC的体积
此题证法很多,下面用割补法证明如下:
解法1:如图3,连结AD、PD
因为BC⊥DE,BC⊥AP,所以BC⊥平面APD,又D E⊥AP,所以VP-ABC=VB-APD+VC-APD
解法2:如图4,以三棱锥P-ABC的底面为底面,侧棱PA为侧棱,补成三棱柱PB1C1-ABC,连结EC、EB,则易证AP⊥平面EBC。
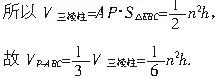

六、等积转化
等积法就是借助面积或体积相等,求解线段的长度等问题。

例6:如图5,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥A1-EBFD1体积。
解:易证四边形EBFD1是菱形,连结A1C1、EC1、AC1、AD1,则
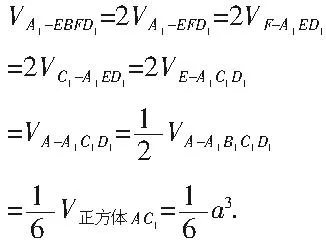
在数学操作中实施转化时,我们要遵循熟悉化、简单化、直观化、标准化的原则,即把我们遇到的问题,通过转化变成我们比较熟悉的问题来处理;或者将较为繁琐、复杂的问题,变成比较简单的问题,按照这些原则进行数学操作,转化过程省时省力,经常渗透转化思想,可以提高解题的水平和能力。

