基于卡尔曼滤波的TDM网络时钟同步方法研究*

寸天睿

(楚雄师范学院信息科学与技术学院，云南 楚雄 675000)



基于卡尔曼滤波的TDM网络时钟同步方法研究*

寸天睿

(楚雄师范学院信息科学与技术学院，云南 楚雄 675000)

网络时钟同步是TDM网络中必须要考虑的关键问题，其中采用IEEE1588时钟同步协议的软件同步方法在高精度同步场合应用广泛。如果时钟同步过程中链路不对称会引入时间数据偏差问题，采用同步补偿的方法从一定程度上改进了时间同步精度，但该类方法没有考虑环境噪声的问题，容易造成TDM网络不稳定。本文提出一种基于卡尔曼滤波的TDM网络时间间接补偿方法，对时钟同步获取的信息先进行卡尔曼滤波降噪处理，然后再通过频率调整进行时间间接补偿，在提高同步精度的同时，提升了TDM网络的稳定性。

TDM网络；卡尔曼滤波；时钟同步

1.引言

在时分复用(Time Division Multiplexing, TDM)的网络中必须要考虑的一个关键问题就是网络时间同步。在TDM网络中通常每个通信节点都包含一个时钟，各个通信节点按照时间顺序有序的向网络中发送数据，降低时钟同步误差是维持整个网络稳定运行的关键。目前时钟同步的常用方案有使用时钟同步协议进行软件方式同步和硬件方式同步两种，其中采用IEEE1588时钟同步协议的软件同步方法在高精度同步场合应用很广泛，如无线传感器中网络的时钟同步[1]，以太网中的时钟同步[2]和城域网中的时钟同步[3]等。但是，由于IEEE1588协议本身并没有考虑通信链路噪声，链路对称性问题和时间戳标记误差对时间数据带来的影响，因此需要对时钟进行补偿调整。

针对时钟同步过程中链路不对称引入的时间数据偏差问题，文献[4]和文献[5]通过修改协议中计算时间偏差的方式来提高同步精度；针对时间戳标记误差，文献[6]和文献[7]通过设计高速硬件电路来减少由软件执行引入的误差。这些方式从一定程度上改进了同步精度，但没有考虑环境噪声的干扰。针对环境噪声的问题，文献[8]引入卡尔曼滤波器对接收到的时钟偏差进行滤波预处理从而提高时间同步数据精度，文献[9]在文献[8]的基础上使用卡尔曼滤波，同时对时钟偏差和频率数据进行滤波处理，大大提高了同步精度。然而以上的方法采用的都是时钟偏差直接补偿的方式，这种补偿方式在时分复用的控制网络中会带来时间补偿后的突变，造成系统运行不稳定[10,11]。因此如何对时钟同步过程进行数据滤波降噪处理和合理的补偿是生产实际中TDM网络能否稳定运行的关键之一。

本文提出一种基于卡尔曼滤波的频率间接补偿方法。对同步协议获取的时间偏差采用卡尔曼滤波提高偏差精度然后对计时时钟管理单元的计时频率进行调整，达到间接补偿时间偏差的目的，提高时钟同步的精度和系统的稳定性。本文研究首先对IEEE1588时钟同步模型及传统的直接同步补偿方式进行说明并阐述存在的问题；然后对基于卡尔曼滤波的频率间接补偿进行研究；再次通过仿真分析证明本文提出方法的有效性；最后对全文所做的工作进行小结。

2.IEEE1588时钟同步补偿分析

2.1 TDM时钟同步模型和误差分类

时钟同步误差可归为三类，时间偏差，频率偏差和频率漂移[12]，时钟时间偏移示意图如图1。将从时钟在时刻Tn读取的时间值记为C(t)，将在时刻n的默认准确参考时间值记为T(n)=t。并定义以下误差表示方式，如无特殊说明，后续将沿用这种表示方式：

(1)时间偏差：时钟时间与标准参考时间的偏差，令θ(t)表示时间偏差则有：

θ(t)=C(t)-t

(1)

(2)频偏率：通常采用频偏率来衡量频率偏移程度[15]。则频偏率γ计算如式(2)，其中fT为标准频率值，fi为从节点时钟频率值。

(2)

(3)频率漂移：由所处环境的改变而造成的长期的频率改变。本文采取的补偿机制在每个短时间周期内进行，所以相对来说长时间发生的频率漂移可视为常量，本文不做讨论。

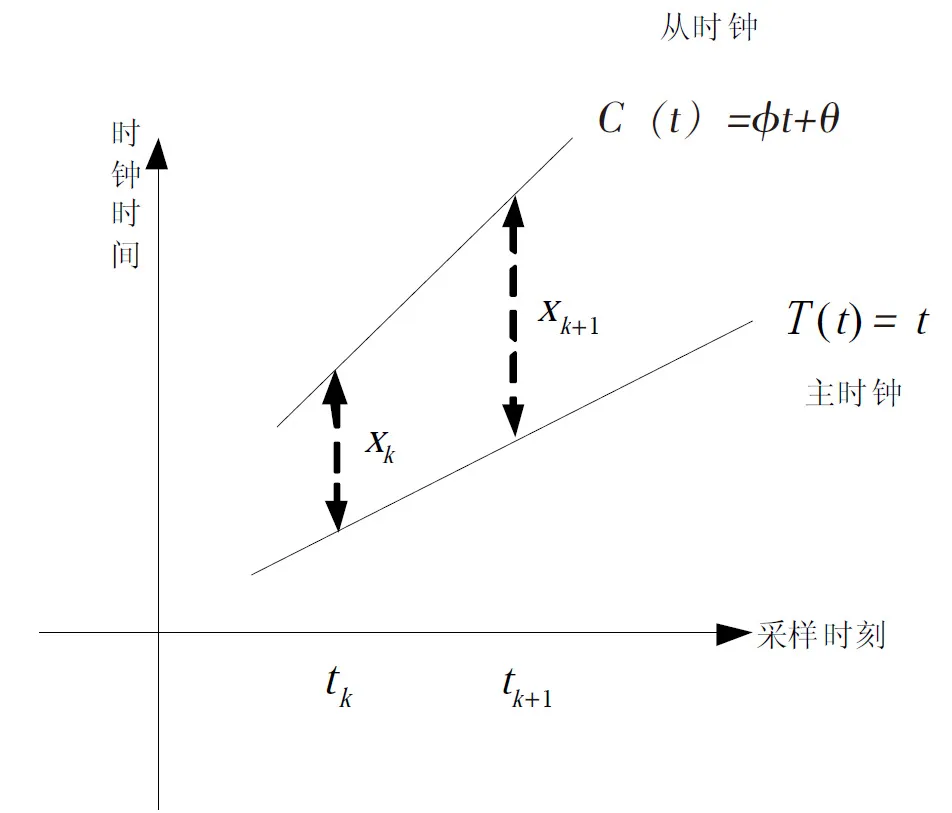
图1 网络时钟时间偏移示意图

为分析方便，本文引入状态变量模型对节点时钟进行分析和描述，状态变量模型在很多先前的研究中被采用，如参考文献[9]、[13]中采用状态变量模型对时钟进行建模。时钟补偿主要针对时间和频率这两个变量，文献[14]采用两个状态变量的模型进行分析，这种模型也是嵌入式系统时钟管理模块分析中常采用的数学模型，本文也采用这种模型进行分析。时钟管理模块的输出电压由式(3)给定，其中fT是编程设定的时钟计数频率，Φ0是初始相位，Φ(t)是影响时间精度的随机过程，为不失一般性可设Φ(t)期望E[Φ(t)]=Φ0。

(3)

由于相位噪声对基于IEEE1588协议的时钟同步方法没有影响[15]，从而得到时间偏差的离散递归表达式(4)，其中ΔT=Tn-Tn-1。

θ(n+1)=θ(n)+γ(n)ΔT

(4)

θ(n+1)=θ(n)+γ(n)ΔT+ωθ(n)

(5)

γ(n+1)=γ(n)+ωγ(n)

(6)

2.2直接时差补偿机制

直接时差补偿机制在计算出时钟偏差后直接对从时钟时间进行加减补偿，其补偿流程如图2示。这种补偿方式是IEEE1588定义的补偿方案，该方案用主从时钟节点交换数据报文计算出的时钟偏差值对从节点时钟值进行直接加减。在文献[11]等研究中采用通过增加冗余节点，设计硬件时戳发生器等方案对计算出的时钟偏差进行直接补偿。近年来由于卡尔曼滤波算法在各个领域的广泛应用，在[9]、[10]等文献中采用卡尔曼滤波对计算出的时间偏差先滤波，进行偏差准确性评估和预测后再直接补偿，通过仿真验证效果良好。

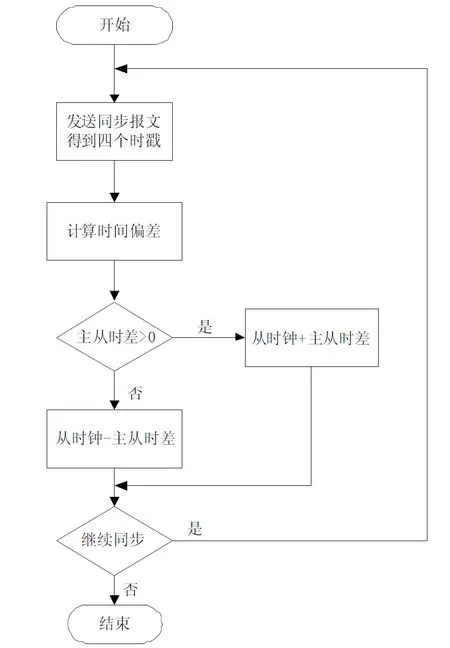
图2 网络时钟同步直接时差补偿流程图

但是，在分布式网络控制系统中，直接补偿将会使从节点时钟产生突变和较大的波动，出现“时间快进”和“时间逆流”等不稳定现象[10][11]。文献[10]提出通过IEEE1588协议得出时间偏差后对时钟频率进行补偿的渐进补偿方法，但是没有考虑对获得的时间偏差进行降低噪声的处理，对渐进式补偿只提出展望没有具体实现。在实际网络控制系统中，由于各个受控器件严格按照时序响应命令并采取相应调整行为，而时钟经过直接补偿产生突变将会造成系统不稳定。

图3 时钟直接补偿示意图

3.卡尔曼滤波频率间接补偿

3.1卡尔曼滤波的特性

目前，很多专家学者对卡尔曼滤波技术在时钟同步补偿中的应用进行了研究。如在文献[16]中对卡尔曼滤波在全球定位系统时钟同步中的补偿进行了研究。在文献[17]中对卡尔曼滤波技术在无线网络时钟同步中进行频率跟随进行了研究，在文献[18]中对将卡尔曼滤波用于网络时间协议中进行数据预处理提高系统稳定性进行了研究。

通过对已有文献的研究，可以归纳得出卡尔曼滤波的三个重要特性：

(1) 当被跟随信号的方差呈高斯分布时卡尔曼滤波是最优估计方法。在文献[19]中已证明由于时钟变动叠加导致的偏差近似服从高斯分布。

(2) 卡尔曼滤波增益决定了滤波器的带宽。可以通过合理的选择滤波参数，在测量噪声的同时不改变滤波延迟。

(3) 卡尔曼滤波算法可以通过软件和硬件方式实现且实现容易。

图4 卡尔曼滤波频率间接时差补偿流程图

基于以上三点特性，下节将使用卡尔曼滤波方法对时间偏差进行更精确的估计和补偿。

3.2卡尔曼滤波频率间接时钟补偿机制

对时间误差的直接补偿会使时间突变造成TDM网络系统运行不稳定，如上节所述，由式(5)时间偏差和频率偏差的关系可知，对时间偏差的调节也可以通过频偏比进行调节，综合频偏和时间偏差值对从节点的记时时钟管理单元计数频率进行调节，即当从节点时钟慢于主时钟时，加快从节点计数频率，使其时钟频率加快，在下一个同步时钟周期到达时尽量缩小时间偏差；当从节点时钟快于主时钟时，降低从节点时钟计时器计数频率，使其计数频率减慢，等待主时钟节点跟近。考虑到时钟偏差的精确度对整个补偿过程至关重要，所以下文提出一种采用卡尔曼滤波估计的间接时差补偿方法，对得到的时差和频偏先进行卡尔曼滤波提高数据准确度，然后对时钟管理模块计数频率进行间接补偿调整，调整结束后的值再返回到系统中进行新一轮的卡尔曼滤波和调整，整个补偿机制示意图如图4所示。

为了达到主从时钟同步，在时刻n将时差校正uθ(n)和频偏率校正uγ(n)输入式(5)和式(6)所建立的状态时钟模型可得式(7)和式(8)。

θ(n+1)=θ(n)-uθ(n)+[γ(n)-uγ(n)]·ΔT+ωθ(n)

(7)

γ(n+1)=γ(n)-uγ(n)+v(n)

(8)

由于有干扰的存在，时差和频偏信息存在误差，本文采用卡尔曼滤波方法对频率补偿进行滤波预处理。将上述两式合并写成矩阵形式如式(9)：

x(n)=Ax(n-1)+Bu(n-1)+ω(n-1)

(9)

其中：u(n)=[uθ(n),uγ(n)]T是输入向量，x(n)=[θ(n) γ(n)]T是状态向量，矩阵A和B分别为式(10)和(11)，ΔT为IEEE1588同步报文Sync的报文间隔：

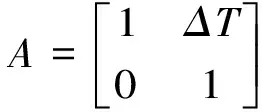
(10)

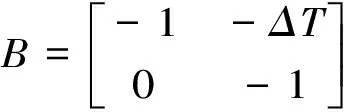
(11)

定义θM(n)为时刻n时的测量时间偏差，如式(12)。其中γM(n)是时刻n时的测量频偏率。则有：

(12)

由此，可以定义卡尔曼滤波测量方程如式(13)：

z(n)=Hx(n)+v(n)

(13)

定义了上述方程后，就可以得出卡尔曼滤波的五个方程[20],这五个方程在很多介绍卡尔曼滤波的教材中都有讲述。

(14)

P(n|n-1)=AP(n-1)AT+Q

(15)

卡尔曼滤波增益为式(16)：

K(n)=P(n|n-1)[P(n|n-1)+R]-1

(16)

卡尔曼滤波校正过程方程可以定义为式(17)和式(18)：

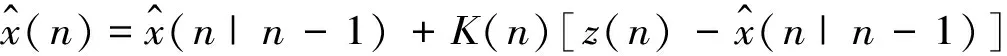
(17)

P(n)=[I-K(n)]P(n|n-1)

(18)

其中R是二阶测量噪声协方差矩阵，根据θM(n)和 γM(n)关系有：

(19)

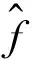
(20)

通过时钟同步协议进行同步报文交换，得到时刻n时候从时钟与主时钟的时间偏差θM(n)，则如果期望从时钟在主时钟经历固定周期△T到达n+1时达到同步，则从时钟时钟管理单元计时频率fs按式(21)设置为：

(21)

所以从时钟节点的频率补偿值Δfs设置为式(22)：

(22)

将式(15)带入得到化简后的频率补偿式(23)。

(23)

θM(n)通过时间同步交换同步报文获得的时间戳计算得到，得到θM(n)后计算得出频偏比的测量值γM(n)，经过卡尔曼滤波输出的评估值γ(n)作为调整参考，根据式(23)对从节点时钟进行频率调整，从而减少时间偏差，由于环境中温度，电磁干扰等噪声的存在，频率的调整不能一步到位，整个频率调整过程循环往复，逐渐趋向主时钟频率，从而到达间接补偿时间偏差的目的。

4.仿真分析

(1)时钟偏差直接补偿与时钟偏差频率补偿

图5 直接补偿与频率补偿的时钟偏差

对时钟采取时钟偏差直接补偿和时钟偏差频率间接补偿后的对比如图5示。在仿真开始的前200ms由于没有进行时钟补偿，主从时钟偏差值越来越大。从200ms开始，每隔100ms分别对时钟偏差进行直接补偿和频率补偿，整个仿真过程中加入了噪声干扰，因此时钟偏差值存在小幅抖动。

如图5所示直接时钟补偿在每次补偿时由于直接调整从时钟的时间值，造成时间突变，同时由于没有调整时钟频率，主从时钟偏差在每次补偿结束逐渐拉大。频率补偿方式通过调整时钟计数频率的方式进行补偿。每次补偿后，从时钟时间值连续变化，主从时钟时间偏差渐近的缩小，每一个补偿周期的时钟偏差与上一个补偿周期的时间偏差范围相比越来越小。

对比两种补偿方式可以看出，频率补偿方式虽然没有直接补偿时差调整速度快，但在400ms时，经过4次补偿后，时钟偏差变化范围已经小于0.2ms，而直接补偿在400ms后的时钟偏差变化范围还在1.8ms上下浮动。因此频率补偿的时钟同步的精度得到了很大提高。同时由于频率补偿的时间变化过程是连续的，能保证存在时间触发事件的通信网络稳定运行。

(2)无卡尔曼滤波时钟频率补偿与卡尔曼滤波时钟频率补偿

仿真对比了加入卡尔曼滤波和没有加入卡尔曼滤波的频率补偿方式的时钟偏差，由于在整个过程中加入了噪声干扰，时钟偏差值存在小幅抖动，如图6所示。仿真前200ms由于没有进行时钟补偿，主从时钟偏差越来越大。从200ms开始每隔100ms对时钟偏差值分别进行卡尔曼滤波处理后的频率补偿和不经过卡尔曼滤波的频率补偿，两种情况都能使从时钟以渐近的方式缩小与主时钟的时钟偏差。但引入卡尔曼滤波对时钟偏差值进行降噪处理后，时钟差值的精度得到了提高，使得补偿结果相比没有引入卡尔曼滤波更为精确，整个时钟偏差的变化趋势更为平滑。

图6 有无尔曼滤波的频率补偿时钟偏差

5.小结

本文对TDM网络中的精确时钟同步技术做了深入的研究。分析了直接时钟补偿对TDM网络运行带来不稳定的原因并提出一种采用卡尔曼滤波的时钟频率间接补偿方法。该方法通过对同步获取的信息进行滤波处理降低噪声干扰，提高了时差数据的准确性，然后对时钟计数频率进行补偿，通过这种方式间接改进时钟偏差，在提高时钟同步准确度的同时保证了系统的稳定性。

[1] Sung H., Kyeong P., Doo-Seop E.. Energy-efficient and rapid time synchronization for wireless sensor networks[J]. IEEE Transactions on Consumer Electronics, 2010, 56(04): 2258―2266.

[2] Chenglong Q., Feng J.. Research and design of industrial Ethernet switch based on IEEE1588 standard[A]. IEEE International Conference on Advanced Power System Automation and Protection[C]. 2011.

[3] Alcatel L., Murray H.. A synchronization algorithm for packet[J]. Communications. IEEE Transactions on Communications, 2011,59(04):1142―1153.

[4]Shuai L.. An enhanced IEEE 1588 time synchronization for asymmetric communication link in packet transport network[C]. IEEE Communication Letters, 2010, 14(08): 764―766.

[5]Simanic N.. Compensation of asymmetrical latency for ethernet clock synchronization[A]. International IEEE Symposium on Precision Clock Synchronization for Measurement Control and Communication (ISPCS)[C], 2011.

[6]Wenjun H.. Hardware-based solution of precise time synchronization for Networked Control System[A]. IEEE International Conference on Electronics, Communications and Control[C], 2011.

[7]Yang K.. A new design for precision clock synchronization based on FPGA[A]. 16th IEEE-NPSS Conference on Real Time[C], 2009.

[8]Bletsas L.. Evaluation of Kalman filtering for network time keeping[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2005, 52(09): 1452―1460.

[9]Giorgi G.. Performance analysis of kalman-filter-based clock synchronization in IEEE 1588 networks[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(08):2902―2909.

[10]张建斌. 基于工业以太网的列车通信网络研究[D]. 北京: 北京交通大学, 2011.

[11]Weidong Y.. IEEE1588 clock servo algorithm[A]. 9th International Conference on Electronic Measurement & Instruments[C], 2009.

[12] Aziz M.. The use of ethernet for single on-board train network[A]. IEEE International Conference on Networking, Sensing and Control[C], 2008.

[13] Scheiterer L.. Synchronization performance of the precision time protocol in industrial automation networks[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(06): 1849―1857.

[14] Fuchs E.. The future of silicon photonics: not so fast insights from 100G ethernet LAN transceivers[J]. IEEE Journal of Lightwave Technology, 2011, 29(15): 2319―2326.

[15]乔英忍. 世界铁路动车组的技术进步水平和展望[J]. 国外铁道车辆, 2007, 44(03): 7―8.

[16] Zuohu L.. High Precision Clock Synchronization and Control Based on GPS[A]. IEEE International Conference on Electrical and Control Engineering[C], 2010.

[17] Abubakari L., Hedayat A.. IEEE 1588 style synchronization over wireless link[A]. IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication[C], 2008.

[18] Aziz M.. The use of ethernet for single on-board train network[A]. IEEE International Conference on Networking, Sensing and Control[C], 2008.

[19]Ferrari P.A distributed instrument for performance andysis of real-time ethernet networks[J]. IEEE Transactions on Industrial Informatics, 2008,4(01):16―25.

[20]Welch G., Bishop G.. An introduction to the kalman filter[Z]. Department of Computer Science, University of North Carolina, July 2006.

(责任编辑 刘洪基)Research on the Clock Synchronization Method of TDM Network Based on Kalman Filter

CUN Tianrui

(SchoolofInformationScience&Technology,ChuxiongNormalUniversity,Chuxiong, 675000,YunnanProvince)

The important issue of the TDM network is precise time synchronization. The software synchronization method using the IEEE1588 clock synchronization protocol is widely used in the high precision synchronization.If the link of the time synchronization process is asymmetrical, it will introduce time data deviation. Using synchronous compensation method will improve time accuracy to a certain extent, but this method does not consider the problem of environmental noise which is easy to cause the network system instability. This paper presents a method of TDM network clock indirect compensation based on Kalman filter. The information of the time synchronization is firstly denoised by Kalman filter, then clock is adjusted by the frequency indirectly to compensate the time. This method can both improve the time synchronous accuracy and enhance the stability of TDM network.?

TDM network; Kalman filter; time synchronization

2016 - 05 - 26

寸天睿(1987―),男，硕士，助教，主要研究方向：网络计算。

TP393.01

A

1671 - 7406(2016)09 - 0057 - 08