从特殊到一般破表象明实质——一道中考压轴题的解题教学分析

朱玉祥（江苏省南京市第2929中教育集团致远校区）

从特殊到一般破表象明实质
——一道中考压轴题的解题教学分析

朱玉祥（江苏省南京市第2929中教育集团致远校区）

探究类问题的结构通常是先给出几个小问题，在对小问题探究的过程中，积累获得知识与方法的经验，接着就转入问题解决.要解决的问题与小问题相关而又有一定的变化.能不能顺利解决问题，一要取决于对小问题探究的经验，二要取决于对小问题探究经验的迁移能力与认知高度.因此，解题教学中，要引导学生先积累特殊性经验，再提升一般化认识.

问题探究；经验积累；从特殊到一般；数学联系；数学本质

笔者最近给学生讲了一道问题探究类的题目.这类题目的结构是：先给出小问题让学生探究；然后题锋一转，就进入问题解决.一般来说，探究的小问题往往和要解决的问题相关，或是方法相关，或是解决问题和小问题探究中获得的结论相关.

然而，经验未必就能解决所有问题.讲这道题时，以往经验让学生在解题时出现了错误.下面笔者谈谈在这道题的解题教学过程中是如何引导学生完成问题解决的.

一、思维阻滞

1.原题呈现

题目（2013年陕西卷第25题）问题探究：

（1）试在图1（1）中作出两条直线，使它们将圆面四等分.

（2）如图1（2），M是正方形ABCD内一定点，试在图1（2）中作出两条直线（要求其中一条直线必须过点M），使它们将正方形ABCD的面积四等分，并说明理由.

问题解决：

（3）如图1（3），在四边形ABCD中，AB∥CD，AB+ CD＝BC，点P是AD的中点.如果AB＝a，CD＝b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.

图1

2.尝试解答

学生拿到题目比较兴奋，认为第（1）小题和第（2）小题太容易了，几乎没做太多的思考，就开始画图.进入第（3）小题，课堂安静下来了.笔者看到，有学生借第（1）小题和第（2）小题的经验，尝试过点P画AD的垂线（如图2）.笔者就问：这条直线能平分四边形ABCD的面积吗？能说出道理吗？学生想了想，发现所分的两部分面积并不相等.解决问题的思维受阻.

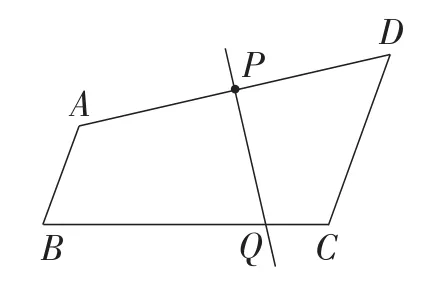
图2

3.思维受阻分析

“问题探究”的两道小题应该是问题解决的起点，但这两道小题选取的图形都非常特殊，一个是圆，一个是正方形，都是中心对称性图形，而第（3）小题是梯

形，有本质的改变.第（1）小题与第（2）小题问题接近，没有形成一定的探究梯度，而第（3）小题又高高在上，缺少铺垫，因而思维受阻.思维受阻的关键，是学生不能突破第（1）小题与第（2）小题的表象，不能从特殊到一般地做关联性探究.所以，讲题要设计相应的教学环节，给学生以引导.

二、问题再探

1.寻找关联

（1）从图形看关联.第（1）小题与第（2）小题所给的图形都是中心对称图形，那么，第（3）小题的图形会不会也能变换转化成中心对称图形？研究图1（3），因为点P是AD的中点，不妨尝试旋转变换，把四边形ABCD绕点P旋转180°后，再判断旋转前后的图是不是中心对称图形.

（2）从题目要求看关联.第（1）小题与第（2）小题是用两条直线把所给图形的面积四等分（两条直线都过图形的对称中心），如果沿着其中一条直线剪开来，取其一半，题目就改变成用一条直线把一半图形面积两等分.如图3是第（1）小题取其一半后的图，图4是第（2）小题取其一半后的图.这样，第（3）小题和第（1）小题、第（2）小题的解题要求就比较接近了.

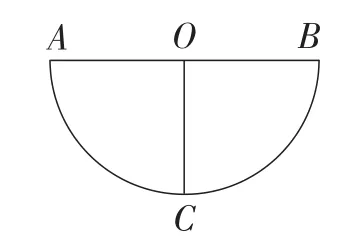
图3

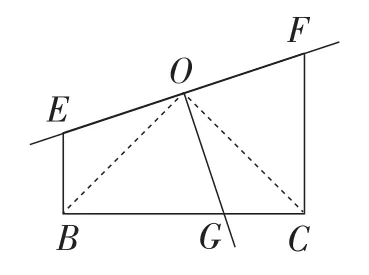
图4

2.突破表象

过对称中心且互相垂直的两条直线是四等分图形面积的本质吗？先来看圆，用两条直线把圆的面积四等分，直线必须过圆心且分成的图形必是全等的扇形.那么画图就要从四等分圆周开始.而弧相等，它们所对的圆心角等，就得到四个90°的圆心角，于是就有了两条互相垂直的直径.所以，用两条直线四等分圆的本质应是四等分圆周.

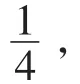
图5

3.特例分析

（1）之所以说垂直不是本质，是因为过对称中心的两条互相垂直的直线并不一定能把该图形的周长四等分，也就未必总能把所给图形的面积四等分.不妨来看菱形.

如图6，在菱形ABCD中，AC，BD交于点O，则点O到菱形ABCD的四边距离相等.过点O任作直线EF⊥HG，分别交AB，BC，CD，AD于点E，G，F，H，显然，要想S四边形EBGO＝S△OBC，必须S△OEB＝S△OGC，所以必须BE＝CG才行.可是，EF⊥HG并不能保证有BE＝CG.所以，过对称中心的两条互相垂直的直线只能把圆和正方形的面积四等分（也能把偶数边的正多边形面积四等分），不能把菱形的面积四等分.

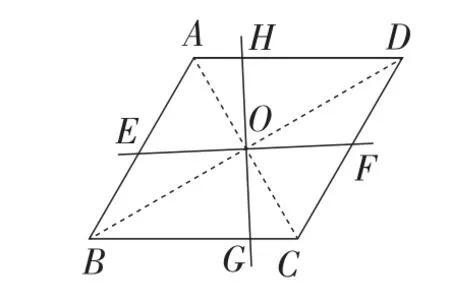
图6

（2）如果中心对称图形的对称中心到各边的距离不相等，那么面积四等分线如何等分其周长呢？以矩形为例.

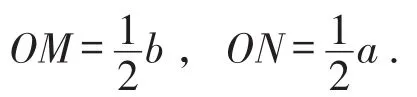
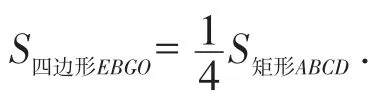
可以看到，中心对称图形的对称中心若到各边的距离不等，四等分该图面积的两条直线分其周长应与对称中心到各边的距离的比值相关.

三、问题解决

1.延伸思考

要解决第（3）小题，先从第（1）小题到第（2）小题的延伸方向来思考.边的延伸：圆→正方形→菱形；角的延伸：圆→正方形→矩形；更一般化的延伸：圆→正方形→平行四边形.再从第（3）小题的条件知识与结论知识之间的数学联系来思考.条件知识是一个两底和等于一腰的梯形通过旋转能得到菱形，结论知识是过另一腰中点的直线两等分梯形面积可从四等分菱形面积获得，它们的数学联系就是过菱形中心存在面积的四等分线.

2.问题解决

解：（1），（2）略.

（3）因为AB∥CD，AB+CD＝BC，点P是AD的中点，

所以将四边形ABCD绕点P旋转180°得菱形C′BCB′，如图8所示.

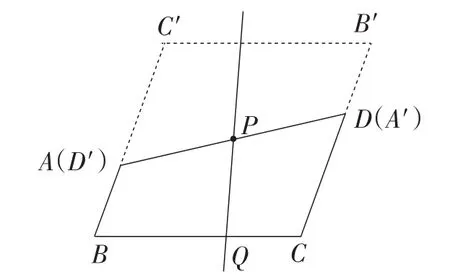
图8

当点Q在BC上，并且CQ＝AB＝a（或BQ＝CD＝b）时，存在直线AD和PQ将菱形C′BCB′的面积四等分，即S四边形ABQP=S四边形PQCD.

所以，在BC上存在点Q，且当BQ＝b时，PQ所在直线将四边形ABCD的面积分成相等的两部分.

求BQ长的过程略.

四、感悟

问题探究类的题目总是先给一些小问题（或特殊问题）探究.这个时候，探究不能止于所给问题，还需要看探究的问题与要解决的问题之间还有多大的间隔，有多少阻碍.探究需要缩小间隔，排除阻碍.例如，探究的问题比较特殊，而要解决的问题又趋于一般化，之间相隔着一般化的认识与探究，就需要把探究的问题延展引申，做一般化的研究，拉近与要解决的问题之间的距离.

问题解决的经验，是关注起始问题提供的起点，一是知识起点，二是方法起点，但经验也要再积累.有的题目从小问题提供的知识起点或方法起点就能直接用于问题解决，有的题目却难以奏效.这时候就必须把起点从特殊向一般转化.当需要解决的问题与所给的起点问题变化比较大的时候，就要提升起点的高度，做更深入的探究，不能停留在原有经验之中.而变化的发现，正是要从解题中感悟和积累.

［1］章建跃．在“落实立德树人根本任务全面深化课程教学改革”中再立新功［J］．中国数学教育（初中版），2015（1/2）：2－4．

［2］董林伟．从形式走向本质：关于初中数学探究活动教学的思考［J］．中国数学教育（初中版），2011（11）：2－5．

2016—07—07

朱玉祥（1955—），男，中学高级教师，主要从事初中数学教育教学研究．