抓特征找规律解一题会一类
——对一道中考选择题求解的前思后想
沈岳夫(浙江省绍兴市柯桥区平水镇中学)
抓特征找规律解一题会一类
——对一道中考选择题求解的前思后想
沈岳夫(浙江省绍兴市柯桥区平水镇中学)
中考试题往往具有代表性、典型性、示范性.可通过研究把蕴涵于试题中的数学思想方法揭示出来,挖掘出隐含的问题的本质属性.通过对2015年湖北省武汉市一道中考选择压轴题的研究,归纳出解决这类问题的思想与方法.通过对一类含有相同“定线张角”基本模型试题的研究,既能让学生夯实基础,又能达到“知一形,晓一类,通一片”的效果.
中考试题;定线张角;基本模型;方法应用
波利亚在《数学的发现》一书中提出了“教师十诫”,其中第八诫是要找出手边题目中那些可能对后来题目有用的特征,即揭示出隐藏在当前具体情形中的一般模型.因此,对试题的研究是教师在教学和复习中经常做的一件事,通过研究把蕴涵其中的数学思想方法揭出来,挖掘出其隐含的问题的本质属性.这不仅有利于学生掌握基础知识,而且有利于学生拓宽思路、活跃思维,较好地发挥中考试题的潜在功能.本文以2015年湖北省武汉市中考数学试卷的最后一道选择题为例,做一些探索,以期抛砖引玉.
一、考题呈现,方法提炼
题目(2015年湖北·武汉卷)如图1,△ABC,△EFG均是边长为2的等边三角形,点D是边BC,EF的中点,直线AG,FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( ).

图1
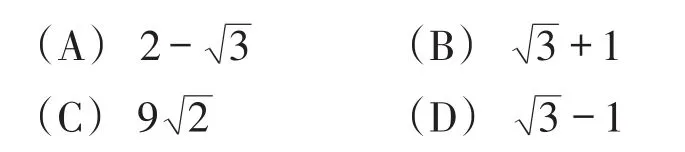
分析:由题意可知,虽然△EFG绕点D在旋转,但是△ABC是固定不动的,且∠AMC所对的边始终是线段AC,由此可猜想∠AMC(动角)在以线段AC(定线)为直径的圆上运动,这样可以构造出辅助圆,便能取得简洁、明快的效果.
解:如图2,连接AD,DG.

图2
由题意知AD=DG,DC=DF,
则△DAG和△DCF都是等腰三角形.
根据旋转的性质可知∠ADG=∠CDF=α,
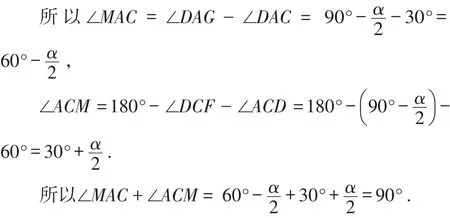
所以∠AMC=90°.
故动点M的轨迹始终在以AC为直径的圆上.
现以AC为直径作圆,设圆心为O,连接BO,与⊙O相交于点P,
则线段BP的长即为线段BM长的最小值.
故此题选D.
【评析】此题要求“当△EFG绕点D旋转时,线段BM长的最小值”,只需证明∠AMC=90°,说明∠AMC的大小固定,且∠AMC分别经过两个定点A,C,线段AC的长度固定,即存在两点(即定线);但∠AMC的顶点M是动点,即一动(即张角).因此,此题的条件中存在两点一动.反思此题的解题过程,是根据定理“在同一圆中,同弦(同侧)所对的圆周角相等”,可知该题中点M应在某个圆上运动.因此,将原问题转化为研究直线与圆的交点问题.
方法提炼:解决这类问题,我们一般可采取“谋定而后动”的策略,先找出动角(张角)所对的边是否为定线,如果是,那么我们就可以构造出辅助圆,然后将问题引向极端,如特殊位置、特殊图形等,使图形更直观、条件更集中,进而简化解题,提高解题速度.那么,对具有两定一动,即一个角的大小固定,且该角的两边分别经过一个动点的试题,是否都可以通过构造辅助圆来解决,也就是说这种“两点一动圆相助”的方法是否具有通适性?
二、应用方法,解决问题
综观近几年的各地中考试题,笔者发现一些中考试卷中还真的有不少题目可以用“两点一动圆相助”作为解题的突破口,使这类题目化难为易,迎刃而解.现采撷数例,剖析解法,以飨读者.
1.找定线,定轨迹,最值问题求解易
例1(2014年四川·成都卷)如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是_______.

图3
分析:由折叠知A′M=AM,又M是AD边的中点,可得A′M=AM=DM,故点A′在以AD为直径的圆上.如图4,以点M为圆心,AM为半径作⊙M.当M,A′,C三点共线时,A′C长度取得最小值.
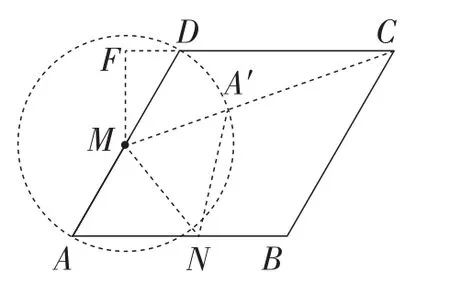
图4
解:如图4,以点M为圆心,AM为半径作⊙M,过点M作MF⊥CD交于点F.
在边长为2的菱形ABCD中,由∠A=60°,
所以CD=2,∠ADC=120°.
所以∠FDM=60°,∠FMD=30°.
【评析】此题在折叠过程中,由题意可知A′M= AM=DM,这样自然联想到圆的定义,所以以点M为圆心,AM长为半径构造辅助圆,则动点A′的轨迹是在以AD为直径的圆上,然后借助圆的知识,建立起已知量与未知量之间的关系,再结合题意化难为易,使问题轻松获解.不难想象,若没想到辅助圆,则难度较大.
例2(2013年湖北·武汉卷)如图5,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是__________.
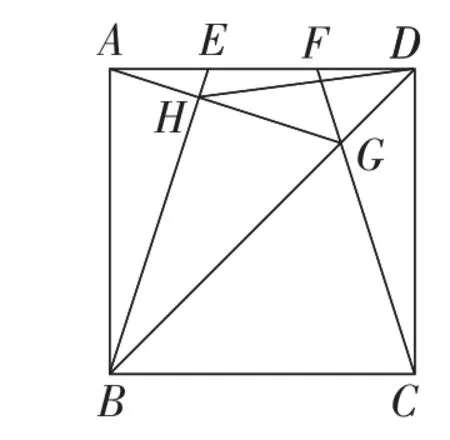
图5
解:由已知易得∠DCG=∠DAG.
又AE=DF,AB=DC,∠EAB=∠FDC,
则△DCF≌△ABE.
所以∠DFC=∠AEB.
结合∠DCG+∠DFC=90°,
得出∠DAG+∠AEB=90°.
从而得∠AHB=90°.
所以点H在以AB为直径的⊙O上(其中O为AB的中点),如图6所示.
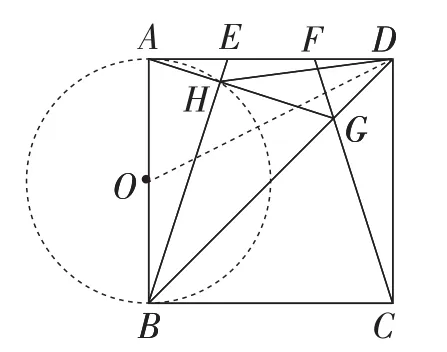
图6
当O,H,D三点共线时,线段DH取得最小值,
【评析】此题与例1相比,看似更难,但经观察、分析和思考,我们可先利用三角形全等证明∠AHB= 90°,这样由90°就想到了直径所对的圆周角等于90°,
因而构造辅助圆.这就告诉我们,解题时应充分挖掘题目中所隐含的信息,即定线AB、张角∠AHB,然后得出答案.这样从题目(包括已知条件、待求结论和图形)中提取一些暗示的信息,实现了快速解决问题.
2.找定线,定张角,坐标问题位置显
例3(2013年内蒙古·呼和浩特卷)在平面直角坐标系中,已知点A(4,0),B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为______.
解:设线段AB的中点为E.
因为点A(4,0),B(-6,0),
所以AB=10,E(-1,0).
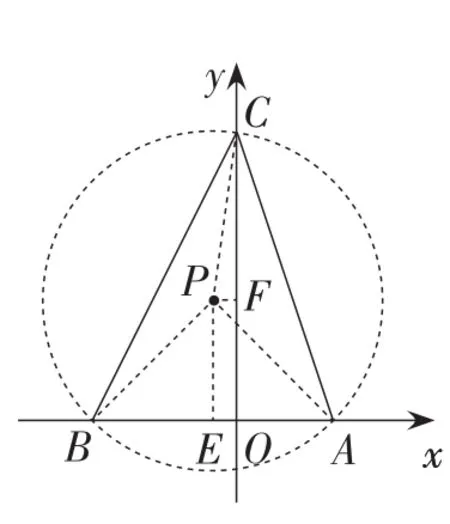
图7
则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=
在图7中以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C.
因为∠BCA为⊙P的圆周角,
过点P作PF⊥Oy于点F,
则OF=PE=5,PF=1.
所以OC=OF+CF=5+7=12,
故点C坐标为C(0,12);
同理,求得y轴负半轴上的点C坐标为C(0,-12).
综上所述,满足条件的点C坐标为C(0,12)或C(0,-12).
【评析】此题与例2相比,看似更难入手.如果直接求解,难度较大,主要的困难在于无法把AO(O为坐标原点),BO这些条件与未知的CO集中到一起,也无法把∠BAC=45°这个条件用进去,导致解题困难.若能换个角度,把45°的角放大,想到90°的圆心角,从定线AB、张角∠BAC=45°入手,作△ABC的外接圆⊙P,这样就找到了解题的突破口.可以说,在中考中,利用辅助圆的策略是对直线型相关求解策略的有益补充.
3.找定线,定圆心,个数问题思路明
例4(2014年山东·淄博卷)如图8,点A与点B的坐标分别是A(1,0),B(5,0),点P
是该直角坐标系内的一个动点.
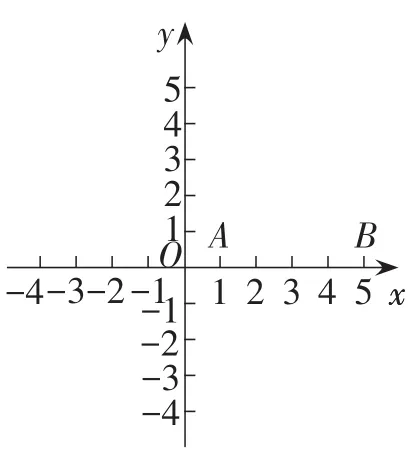
图8
(1)使∠APB=30°的点P的个数有_______.
(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标.
(3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,说明理由.
解:(1)以AB为边,在第一象限内作等边△ABC,以点C为圆心,AC为半径作⊙C,交y轴于点P1,P2.
如图9,在优弧AP1B上任取一点P,
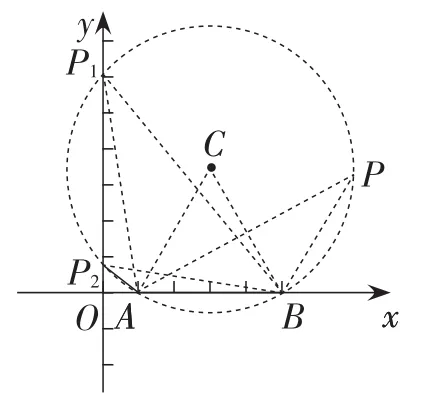
图9
所以使∠APB=30°的点P有无数个.
同理,在第四象限也有无数个.
(2)①如图10,当点P在y轴的正半轴上时,过点C作CG⊥AB,垂足为点G.

图10
由已知易得AB=4,OG=OA+AG=3,AC=BC= AB=4,
在如图10中过点C作CD⊥Oy,垂足为点D,连接CP2,点C的坐标为
又因为P1,P2是⊙C与y轴的交点,
所以∠AP1B=∠AP2B=30°.
因为CP2=CA=4,CD=3,
因为点C为圆心,CD⊥P1P2,
所以P1D=P2D=
②当点P在y轴的负半轴上时,
(3)略.
【评析】此题从题设和结论来看似乎与圆没有什么关系,若能挖掘出图中隐含关系,构造辅助圆,然后再运用圆的定义、性质,便能够顺利地建立起条件与结论之间的联系,进而找到简捷、巧妙的解法,“圆”满地解决问题.可见,解决此题的关键是构造辅助圆.首先是构造经过A,B两点的圆,这样的圆有无数个,圆心都在线段AB的垂直平分线上,然后是构造圆周角是30°的圆,而想到60°的圆心角是关键.
4.找定线,圆相助,范围取值直观看
例5(2014年广东·广州卷)已知平面直角坐标系中两定点A(-1,0),B(4,0),抛物线y=ax2+bx-2(a≠0)过点A,B,顶点为C.点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标.
(2)当∠APB为钝角时,求m的取值范围.
(2)由点P(m,n)(n<0),可知点P在x轴下方.
如图11,设抛物线与y轴交点为点E,点F是点E关于对称轴的对称点,连接AE,BE,AF.
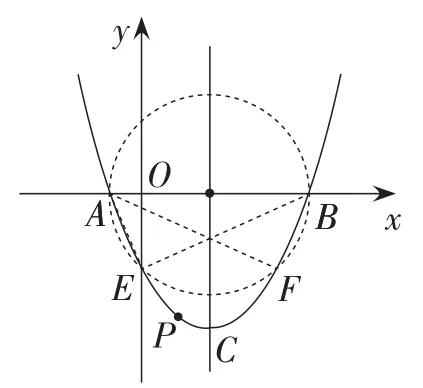
图11
根据题意易证△OAE∽△OEB,
得∠OEB=∠OAE.
所以∠AEB=∠OEA+∠OEB=∠OEA+∠OAE=90°,
所以由抛物线的对称性可知,点F的坐标为F(3,-2),∠AFB=90°.
则以AB为直径作的圆一定经过点E,F,且抛物线上点A到点E,点B到点F的部分都在圆内.
所以当点P在这两部分上运动时,∠APB为钝角.
所以当-1<m<0或3<m<4时,∠APB为钝角.
(3)略.
【评析】此题第(2)小题中,证明∠AEB=90°是关键(除了用相似证明外,还可以运用勾股定理的逆定理加以说明),再由定线AB、张角∠AEB=90°入手作圆,通过构造辅助圆将问题转化为抛物线与圆交点问题,利用对称思想求解.此题若是离散探寻,也会获得满足题意的答案,但易出现漏解.可见,合理挖掘图形隐含的性质,补出辅助圆,就能直观地看出数与形的奇妙联系,从而能有效地解决点P的横坐标的取值范围.
5.找定线,思关联,线段长度分类思
例6(2014年陕西卷)问题探究:
(1)如图12,在矩形ABCD中,AB=3,BC=4,如果BC边上存在点P,使△APD为等腰三角形,那么试画出满足条件的一个等腰△APD,并求出此时BP的长.
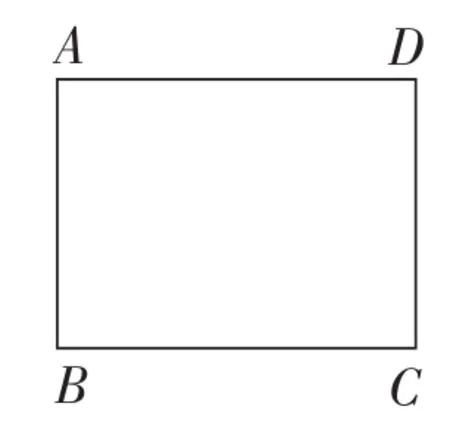
图12
(2)如图13,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E,F分别为边AB,AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长.
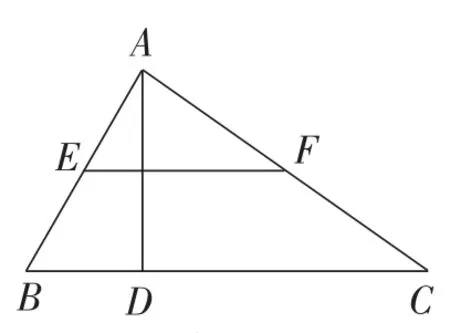
图13
问题解决:
(3)有一山庄,它的平面图为如图14所示的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳.已知∠A=∠E=∠D=90°,AB=270 m,AE=400 m,ED=285 m,CD=340 m,问在线段CD上是否存在点M,使∠AMB= 60°?若存在,试求出符合条件的DM的长;若不存在,说明理由.
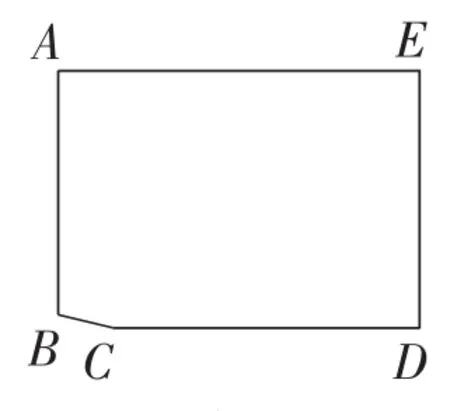
图14
解:(1)略.
(2)如图15,以EF为直径作⊙O,易证⊙O与BC相切,从而得到符合条件的点Q.然后通过添加辅助线,借助于正方形、特殊角的三角函数值等知识,即可求出BQ的长为
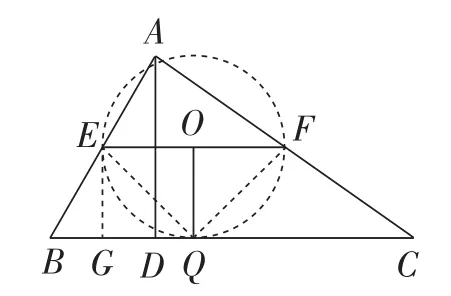
图15
(3)在线段CD上存在点M,使∠AMB=60°.理由如下.
如图16,以AB为边,在AB的右侧作等边△ABG,作GP⊥AB,垂足为点P,作AK⊥BG,垂足为点K.设GP与AK交于点O,则以点O为圆心,OA为半径作⊙O,过点O作OH⊥CD,垂足为点H,
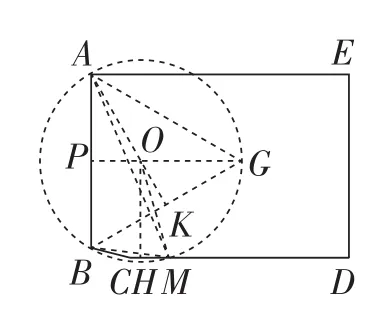
图16
则⊙O是△ABG的外接圆.
因为△ABG是等边三角形,GP⊥AB,
所以OH<OA.
所以⊙O与CD相交.
设交点为M,连接MA,MB,OM,
若点M在点H的左边,
所以DM>CD.
所以点M不在线段CD上,舍去.
若点M在点H的右边,
所以DM<CD.
所以点M在线段CD上.
综上所述,在线段CD上存在唯一的点M,使∠AMB=60°,此时DM的长为米.
【评析】第(3)小题初看似乎与圆毫无联系,主线不明,其实第(1)(2)小题已经布设暗线索.“问题探究”中的两道小题就对应“问题解决”中的两个条件,即如何构造60°,如何让∠AMB=60°,可利用圆来达到目的.对于一类以探究定值、定点、定线为特征的数学问题,可以通过主动寻求或以退为进的策略,巧妙锁定思维的方向,迅速找到问题解决的路径.这样,就大大地避免了探索的盲目性,使思维过程优化变短,显得简洁明快.
通过对上述几个例子的分析,我们不难看出,解综合题时若具备定线、张角,恰当构造辅助圆,则使题目分散的条件集中化,隐含的条件显性化,起到了化难为易、打开思路的效果,或以一题多解,开阔思维,提高解题能力.这种在补形中得以开阔,呈现一片生机蓬勃的新天地,更给人一种流畅、清晰的美感,让我们在解题中不禁惊叹:遇“定线、张角”类试题,“圆”来如此破解.
[1]马先龙.构造图形打开解中考几何最值问题的突破口[J].中学数学杂志(初中版),2014(10):52-53.
[2]戴向阳.动点下的线段最值解法探微[J].中学数学教学参考(中旬),2014(3):37-39.
[3]沈岳夫.构造辅助圆,架起探求综合题的桥梁[J].中学数学(初中版),2013(12):94-96,封底.
[4]何勇波.提炼共性多题同解[J].中学数学教学参考(中旬),2015(3):35-37.
[5]李玉荣.一组最值难题“圆”来如此容易[J].中学数学(初中版),2015(6):90-91.
[6]苑建广.精心雕琢命题方式切实考查数学能力:2011年中考数学特色题归类赏析[J].教育实践与研究(B版),2011(11):48-53.
[7]苑建广.信息转化——问题解决的核心策略[J].中国数学教育(初中版),2012(3):8-11.
[8]朱桂凤.迁移经验方法落实能力目标[J].中学数学教学参考(中旬),2014(8):26-27.
[9]罗琳.合理“预设”激活“生成”:两个教学案例给予的启示[J].中国数学教育(初中版),2013(9):18-20.
2016—07—12
沈岳夫(1963—),男,中学高级教师,主要从事数学教育和数学解题研究.

