发挥题组作用优化教学效果

邢成云（山东省滨州市北镇中学初中部）

发挥题组作用优化教学效果

邢成云（山东省滨州市北镇中学初中部）

题组教学是个古老而又有生命力的话题.若依据教学目标和题组设置的基本原则，通过执教者的精心策划，把相关单题编拟成问题链，凝集成一个有机的整体系统，适时、适地地用好这一整体系统的结构合力，将优化课堂教学的效果，提高学生的学习能力，进而促进教学的长远发展.

题组设计；教学功能；优化教学

题组教学是个古老而又有生命力的话题.说它古老，可追溯到我国古代的《九章算术》；另外，乔治·波利亚（George Polya）编写的《数学分析中的问题和定理》一书也是典范，不仅精选题目，发挥单题的作用，而且在编排上下功夫，发挥题目间结构功能.他在序中说：本书决不是题目的简单汇集，而主要是讲究资料的排列，它应当促使读者独立钻研，并养成合理数学思维的习惯.我们花费了很多精力和时间，仔细地进行题目的编排，这显然是非常必要的.由此可见，在数学教学中，应用题组是合算的，仅用单题显然是白白浪费了题目之间相关性（结构）的教学功能.以上论断足见题组的不凡作用，其旺盛的生命力也彰显出来.

诚然，若题组中的题目彼此不搭界，那这个题组就是一种机械的拼凑，充其量是“1+1=2”，不能很好地发挥它们联手的力量，但若依据教学目标，通过一条主线把它们统摄起来，凝集成一个有机的整体系统，这种系统集成块的适切之用将优化教学的效果，促进教学的长远发展.

以下通过常见的几类题组，进行阐释，交流为盼.

一、题组设计案例

1.铺垫性题组

精心设置垫脚题，步步逼近，达至呼之欲出的境地.在新知识教学中，常常用这一题组，加强学生学习新知识时知识、思维上的铺垫，展示知识的发生过程，找准新知识的生长点，让学生利用已有的知识结构来同化新知识，实现知识的迁移.有时候面对难度较大的题目教学时，也可选用这一方法.

案例1：分式值为0、分式有（无）意义等的现身，常用如下形式铺垫题组，如表1所示.

表1

【说明】通过这一题组，在计算的同时，随机把分式有（无）意义、分式值为0等知识点嵌入，这种铺垫自然、顺畅.

2.并列性题组

这类题组不是简单的平行重复，而是从不同维度、不同视角集中凸显某一知识点、某一方法技能点等的设置，它的使用对突破关键点有实效.

案例2：分式值为0的集中题组.

【说明】通过一组题目，融入诸多干扰因素，凝聚一点，凸显分式值为0的意义，即分子为0，分母不为0，这两个条件缺一不可.

3.递进性题组

题组中的几个问题在思维水平与综合解题能力要求上由浅入深，逐层递进，符合学生循序渐进的学习规律.可以满足不同学生的需要，既给基础较差的学生展示自我的机会，又有可供基础较好的学生进一步探究的空间，使得不同层次的学生都有话可说，都有所收获.

案例3：数学中有好多形式相同但实质不同的题目，学生在处理这类问题稍不留神就会犯下一些错误，带来一些负面影响.如以下试题．

（1）已知等腰三角形的一个底角是50°，则其余两角的度数分别为_______；

（2）已知等腰三角形的一个角是50°，则其余两角的度数分别为_______；

（3）已知等腰三角形的一个角是100°，则其余两角的度数分别为_______；

（4）已知等腰三角形的一个内角是n°，求其余两角的度数.

【说明】此组题中，从一个底角到一个角，再从50°到100°，已经把一些规律包含到里面了，如果条件是一个底角，则所求角有唯一结果；如果条件是一个角，则需考量这个角是底角还是顶角，所求角有两种可能；而把这个角确定为100°，则这个角只能是顶角.一数之差，结果迥异.

通过第（1），（2），（3）小题的变化可知，等腰三角形的内角有这样的规律：①顶角可以是锐角、直角、钝角；②底角只能是锐角.并且在几个问题的解决中渗透了分类讨论的思想，搭起了学生学习的脚手架，把学生由问题浅滩诱入问题深处，再解决第（4）小题对学生来说已是游刃有余了.

可见，这个问题串式题组情境相同，只改变了题中的数据，却引起了解决问题方案的变化，突出了学习内容的思考性，让学生在学习活动中认识到解决问题过程中选择合理方案的重要性，不仅提高了学生运用所学知识灵活地解决问题的能力，而且也提高了学生的认识水平，引发了学生重视对条件与问题的审查与思辨，关注解决问题策略的合理与优化.

4.对比性题组

有意识地设置一组题目，通过对比形成反差，从而凸显差异，引起学生的深度思考，有助于巩固知识和技能，发展思维力.如复习二次函数时，可抓住易混点设置对比题组.

案例4：填空．

（1）二次函数y=2x2-bx+c图象的顶点在原点，则b=______，c=_______；

（2）二次函数y=2x2-bx+c图象过原点，则b______，c=_______.

（3）二次函数y=2x2-bx+3图象的顶点在y轴上，则b=_______；

（4）二次函数y=2x2-bx+3图象的顶点在x轴上，则b=________.

（5）二次函数y=（m2-m）x2-2mx+1的图象与x轴有交点，则m的取值范围是__________；

（6）函数y=（m2-m）x2-2mx+1的图象与x轴有交点，则m的取值范围是__________.

【说明】以上题目每两道题为一小组，貌似相同，实则神离，答案各异.学生在平时的练习中屡有混淆、错误率很高.设计这样的题组，让学生进行比较、分析和综合，提高审题分析能力.在教学中应提醒学生注意：结论的变化是由题目条件的变化引起的.因此，要引导学生三思而后行，通过对比分析，提高审题能力，增强解题的准确性.像这样易错之处用题组的举动，能有效地引起学生对细节的注意，有利于错误的避免与纠正，也是培养学生思维的批判性的有效举措.

5.归纳性题组

这种题组是基于归纳的特点，其中的题目从个别到一般、从具体到抽象，进而概括出一般原理，若再有逻辑推理的助阵，将会完成一个思维的轮回.若根据教学的内容及其规划意图，设置归纳性题组，让学生在解题过程中体验这种思维形式，帮助学生历练知识、技能，积淀数学活动基本经验，能加深学生对数

学规律的认识.

案例5：

（1）如图1，若点O为∠ABC与∠ACB两内角的角平分线的交点，∠A=100°，求∠BOC的度数.

（2）如图2，若点O为∠ABC与∠ACB两外角的角平分线的交点，∠A=100°，求∠BOC的度数.

（3）如图3，若O为∠ABC的内角与∠ACB的外角平分线的交点，∠A=100°，求∠BOC的度数.

（4）若把∠A的度数去掉，试探求以上三道小题中∠BOC与∠A的数量关系.

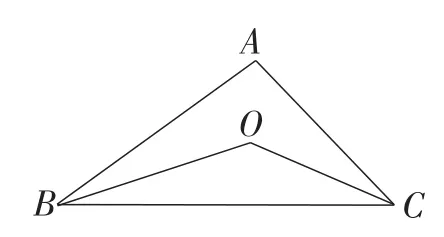
图1

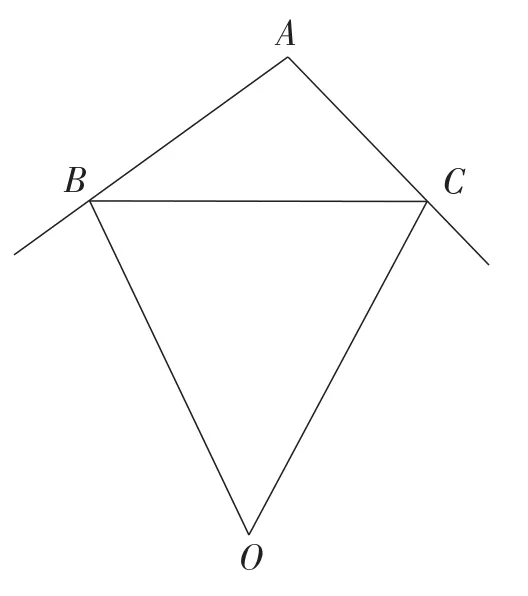
图2

图3

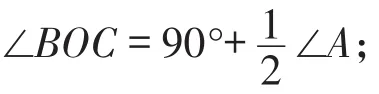
6.构架性题组

通过核心主线把题组并联起来、贯穿起来、统摄起来，尽可能地穷尽模块知识的内涵与外延，有利于全面巩固“四基”，加深理解，形成内在的知识网络.

案例6：复习二次函数，可选用以下题组构建二次函数的网络图.

（1）求此函数的开口方向、对称轴、顶点坐标.

（2）画出这个二次函数的图象.

（3）求图象与x轴、y轴的交点坐标.

（4）当x为何值时，y随x的增大而减小.

（5）当x为何值时，y＞0？y=0？y＜0？

（6）求图象向左平移2个单位，再向下平移2个单位后所得图象的函数表达式.

（7）求图象绕顶点旋转180°后，所得图象的函数解析式.

（8）求图象关于x轴（或y轴）对称的图象的函数解析式.

（9）当x为何值时，函数y有最大值？最大值是多少？

（10）记抛物线与x轴的两个交点为A，B，点C为抛物线上任一点，若△ABC的面积为1，试确定点C的坐标.

【说明】一个题组网尽二次函数的核心知识，把二次函数的图象、性质（顶点、对称性、开口、增减性、最值）、对称变换，以及与方程、不等式的联系等贯通在一起，整体呈现，脉络分明，通过师生的共建，知识网络就形成了.

7.探索性题组

这类题组，它按照一定的组成和线索，出示一组数、式、图、表等，让学生通过观察、实验、计算等数学活动，拨动学生的思维神经，助推学生发现和揭示一些数学规律；或者提出一系列的问题，层级推进，彼此借力，通过题组的合力与张力，把内在的解题规律提炼出来，并把探索的规律用之于解题，这样做不但能激发学生的学习兴趣，而且能培养学生的观察能力、发现与提出问题的能力，以及逻辑思维能力.

案例7：有关基本图形的核心图形——半径、弦的一半以及弦心距的题组.

（1）已知，如图4，AB是⊙O的弦，半径OC⊥AB，垂足为点D.若AB=8 cm，OA= 5 cm，则OD=____；

（2）已知，如图4，AB是⊙O的弦，半径OC⊥AB，垂足为点D.若AB=6 cm，OD=4 cm，则OC= _____；

（3）已知，如图4，AB是⊙O的弦，半径OC⊥AB，垂足为点D.若AB=6 cm，OD= 4 cm，则CD=______；

（4）已知，如图4，AB是⊙O的弦，半径OC⊥AB，垂足为点D.若OC=5 cm，CD=2 cm，则AB=____.

图4

（5）通过上述四个问题的解答，同学们能发现什么？

先思考，再小组交流.

【说明】图中涉及四条与圆有关的重要线段：半径（OA）、弦（AB）、弦心距（OD）、弓形高（CD）.它们的不同组合形成了丰富多彩的题目.通过题组的解答与交流，引导学生把这四个量知其二则能求其另二的规律揭示出来，使之成为解题的有力武器，为它们的后续应用储备能源.

为了将探求出的规律及时显能，可安排一组题作为课后作业.

（1）如图5，AB是⊙O的直径，BC是弦，OD⊥BC于点E，交于点D.

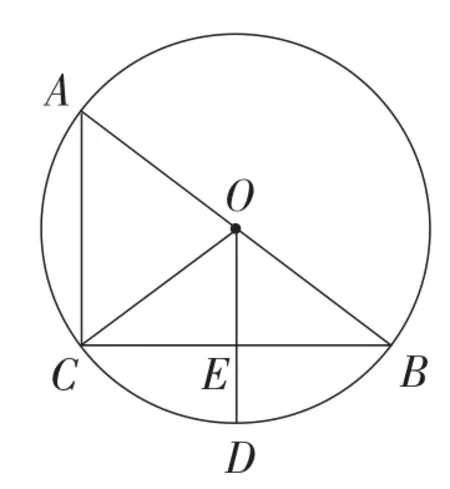
图5

①试写出五个不同类型的正确结论;

②若BC=8，ED=2，求⊙O的半径.

【说明】此题揭示了垂径定理与勾股定理联袂的本质，是对“四条线段”彼此确定最有力的注解.

（2）如图6，已知⊙O半径为5，弦AB长为8，点P为弦AB上一动点，连接OP，则线段OP的最小长度是_______.

图6

【说明】此题表面上并没有要求弦心距，但线段OP的最小长度状态即为OP⊥BA之时，故问题仍然转化为求弦心距.

（3）已知圆的半径为13 cm，两弦AB//CD，AB= 20 cm，CD=10 cm，则两弦AB，CD的距离是（ ）.

（A）7 cm （B）17 cm

（C）12 cm （D）7 cm或17 cm

【说明】基于圆的对称性，此题包括两种情况，求解需将两弦AB，CD的距离转化为两条弦心距的和或差，具有一定的综合性.

通过这一题组作业，让学生感知作弦心距、连半径就是此类题目的常用辅助线，并进一步领悟四量知二求二的解题真谛.

8.规律揭示性题组

案例8：在“坐标系内的图形对称”的中考复习课中，可设计如下题目.

（1）点P(x，y)关于x轴对称的点的坐标是_______；关于y轴对称的点的坐标是_______；关于原点对称的点的坐标是_______.

（2）直线y=2x-1关于x轴对称的直线的解析式是______；关于y轴对称的直线的解析式是_______；关于原点对称的直线的解析式是_______；

（4）抛物线y=3x2+2x-1关于x轴对称的抛物线的解析式是_______；关于y轴对称的抛物线的解析式是______；关于原点对称的抛物线的解析式是______.

【说明】通过题组沿着从点到线，从直线到曲线，递进式发展.通过这种集中呈现，揭示出对称的一般规律，帮助学生构建起解决问题的方法体系——线由点组成，线的对称就是点的对称.因此，关于x轴对称，即将y用-y替换，x不变；关于y轴对称，即将x用-x替换，y不变；关于原点对称，即将x用-x替换，将y用-y替换即可.当通过探研获得这种一脉同源的认识后，就成了以后解决此类问题的有力工具.

二、题组的设置原则

题组的设计要遵循基本原则，力避盲目乱象.题组中的题目之间是有机联系、相辅相成的，它们构成一个小组织、一个小系统.这个组织、这个系统要有规矩，除了恪守科学性原则外，还需遵循以下的基本原则.

1.目的性要强，指向鲜明

题组的设置力避随心所欲的简单的拼盘，力戒“拿到篮里都是菜”的盲目组题，成组要有共同的聚合点，能承担起内化知识、熟练技能、凝聚方法、提升思想的重任.也就是说，目的一定要明确.导向一定要鲜明，是为了以旧引新，还是为了突出重点；是为了化难为易，还是为了归纳提炼等都要了然于心.

2.思想性要强，突出方略

题组设置总有自己的思想脉络，忌简单重复、原地踏步；要有思想、有灵魂，有思维含量.用数学思想武装起来的学生，他们解决问题将更具有洞察力和卓识远见，融入数学思想的题组运用于课堂，我们的教学才会更加朝气蓬勃、充满生机.笛卡儿说过，最有价值的知识是关于方法的知识.突出题组的方法性能、策略价值至关重要，因此，题组教学一定要走出狭隘的以题论题之困境，臻于以题论法之幽境，进而登临以题论道之圣境.

3.阶梯性要强，层级推进

笛卡儿说过，从最简单、最易懂的对象开始，依照先后次序，一步步达到更为复杂的对象.夸美纽斯说过，一切功课都应细分成阶段，务使先学的能为后学的扫清道路，给予解释.两位伟人的经典之言给了我们设置题组教学以极大的启示，明确了题组设置的方向，要遵循学生的认知规律和知识的形成规律，由简到繁，由浅入深，由易到难，层级递进.要用题组中的题目的梯度，逼近学生的最近发展区，以便适应不同学生的不同需求，让不同学生各有所获.

4.启发性要强，启迪智慧

题目的设置要有启发性，要有“不悱不发”的蓄势.富有启发性的题组能不断地激发学生的学习积极性，集中学生的注意力，发展学生的智力，起到举一反三、迁移同化的启迪作用，能启迪思维，启迪智慧，生出求索的欲望.

5.系统性要强，扩张题能

整体效益是题组的追求与归宿！整体效应产生题目的增值，结构体系迸发系统的整合之力.从系统论的观点来看，题组就是一个系统，它不是零星题目的随意组合，更不是题目的堆砌叠加，它贯穿的是融教育规律、教育方法、知识内在联系为一体的一条系统脉络.因此，题组要按照知识的形成过程和相关知识点之间的内在关联来设计，题目组合要有序，搭配要合理.

6.智趣性要强，增进参与

兴趣激发灵感，兴趣增进参与，但单有外在的趣味还不够，还要有数学的真味.外在趣味下的参与是一种浅层的参与，只有靠数学的内在魅力生发的智趣才是内驱力，学生才会为解题而乐此不疲.题组设置的有魅力、有磁力，才能更好地把学习者引入新的思维境界，使学习饶有兴致、富有情趣，并给人以美的享受，助于补偿学生解题之劳顿，提升数学好玩的幸福指数.

三、结束语

通过前面题组的设计与分析，我们看到了题组所特有的功能，它不是独立题目的“物理”组合，单看各个小题没有多大作用，但一组题胶合起来就有了威力，这就是凝聚的作用，集体的力量，也是“组”的核能量.内在的关联是题组的特征，有引领、凝聚、启示、揭示等源动力.

题组不是偶尔为之的营养大餐，而是天天面对的家常便饭，让常态的方法成为习惯，长期的习惯成为意识，长期的意识养成能力，我们的课堂就得到了优化，就有了实实在在的效果.

［1］杨之，陈国清.数学题组刍议［J］.中学数学，1994（5）：15-18.

［2］邢成云.题组引领梯度推进：例谈题组梯度复习法［J］.中国数学教育（初中版），2010（7/8）：34-37.

2016—05—26

山东省教学研究课题——全息教学论下的跨越式教学（pt-20120126）.

邢成云（1968—），男，中学高级教师，主要从事课堂教学与中考研究.