连续梁振动调整的快速解析

李 彤， 李银山， 霍树浩， 韦炳威

(1. 华东理工大学 承压系统与安全教育部重点实验室，上海 200237；2. 河北工业大学 机械工程学院，天津 300130；3. 太原科技大学 机械工程学院，山西 太原 030024)



·实验技术·

连续梁振动调整的快速解析

李 彤1， 李银山2， 霍树浩3， 韦炳威2

(1. 华东理工大学 承压系统与安全教育部重点实验室，上海 200237；2. 河北工业大学 机械工程学院，天津 300130；3. 太原科技大学 机械工程学院，山西 太原 030024)

采用连续分段独立一体化积分法求解了连续梁自振角频率的解析表达式。首先采用弯曲-振动比拟法建立具有四阶导数的挠度微分方程，独立积分4次，得到挠度的通解。利用边界条件和连续性条件确定积分常数，得到挠度的解析表达式；然后根据最小能量原理得到了自振角频率的一次近似解析解；根据渐近法求解精确的振动微分方程得到更精确的挠度解析函数表达式，利用最小能量原理求得自振角频率的精确表达式。按照振动结构的同步失效准则和最优化准则对连续梁支座位置进行调整，得到了结构的固有角频率最优解的解析表达式。绘制了固有角频率随位置的变化曲线。工程实例表明，连续分段独立一体化积分法编程程式化，可以得到自振角频率最优的解析解。

振动调整； 自振角频率； 快速解析法； 最小能量原理； 渐近法

0 引 言

随着科学技术的发展，结构振动的快速解析计算与计算机仿真研究越来越重要[1-9]。自振角频率的调整是一个弹性杆件体系动力学的基本问题，它归结为用各种方法调整弹性体系的刚度或改变对应的位移。在强迫振动时是调整动力和位移的问题，它的计算常与隔振器和减震器的设置，改变作用在结构上的动力传播简图，选择动力作用激振器的工作等有关。振动调整的目的是从调平的条件用方程式的形式表达。通常，总的未知数等于反映与限制目的所要联合求解的方程式数目。但是，由于这些方程的系数部分是位移，所以在一般情况下，这些方程组是非线性的，常用的方法无法求得解析解。

李银山[10]提出的连续分段独立一体化积分法是一种快速求解梁弯曲变形问题的解析方法，文献[11]中利用该方法求解了复杂载荷作用下等截面静定梁的解析解；文献[12-13]中求解了复杂载荷作用下等截面超静定梁的解析解；文献[14]中求解了复杂载荷作用下变截面梁的解析解；文献[15]中求解了杆件体系稳定性问题的解析解。本文利用连续分段独立一体化积分法求解了连续梁振动固有角频率的解析解。

1 支座位置调整连续梁振动固有角频率设计

1.1 问题描述

质量m均匀分布的连续梁(见图1)在怎样的比值l1/L时，它的最低自振角频率最大？已知E，I，L，ρ，A。求ωn，l1。

(a) 中间有1个可调支座

(b) 中间有2个可调支座

图1 可调整中间支座的连续梁

1.2 优化准则

1.2.1 振动设计准则

在电子计算机出现之前，结构优化设计的研究受到计算手段的限制，不能设想全面展开，但是人们还是在构件的优化设计方面做了许多工作，它们大都出自于“同步失效”的概念，也就是构件的各个组成部分同时抵达容许强度或失稳安全限度，由此得出一组联立方程，它们的解析解就提供了构件截面的优化尺寸。用“同步失效”作为优化准则，通常可以得到构件的最轻设计，所以在飞机设计多被采用。对于一根薄壁组合构件来说，它同时有强度、局部稳定和整体稳定问题，采用这种同步失效准则提供的设计公式既方便又有效。对于桁架结构的拉杆或压杆来说，则更为简单，构件优化就是满应力状态，当然要注意压杆的容许应力并不像拉杆的那样是个常数，而是随杆件的细长比而变化的。推而广之，让桁架的每根杆件都成为满应力，这就成为“满应力”准则设计了。对于静定结构来说，由于内力分布不受杆件截面变化的影响，满应力设计就是最轻设计。从直觉出发，人们很自然地把这道理同样也应用于超静定结构。但是在没有电子计算机的时代，要对一个比较复杂的超静定结构在多种工况下完成一个满应力设计也是不容易的。因为要通过多次的迭代才行，而每一次迭代就要进行一次重新分析，计算工作量是非常繁重的，所以过去只得进行一二次迭代得到一个比较轻的设计就满足了。20世纪60年代初，引用数学规划严格地证明了满应力设计和最轻设计并不总是等价的，而且满应力解的存在与收敛也是有条件的。这些条件跟结构本身的构造和荷载情况(工况数目)都有关系。为此，人们做过很多研究，直到现在还没有既十分确切又易于实用的判别方法。但是满应力设计在实际应用中还是很有价值而受到欢迎的。它有下列几个优点：

(1) 有了电子计算机之后，在只有应力约束的问题中这是最简单易行而且通常收敛很快的方法；在兼有变位、频率等其他约束时，也可以作为近似手段配合其它约束组成优化方法。

(2) 满足应力设计虽然在理论上并不一定是最轻设计，但是实践表明两者在很多场合常常是相等或者很接近的。

(3) 在优化过程中，每走一满应力步后，紧接着走一射线步(或称比例步)把设计点引到可行域边界上，如此交替进行，就可以把满应力准则跟目标函数联系起来得到最轻解；这就是所谓改进满应力法，或称满应力齿行法。它给出的结果已不是满应力解，实际上它是一种数学规划结合力学特点的搜索法。因为它一是利用满应力条件来决定搜索方向和步长，二是利用射线步把设计点拉回可行区的边界；这两者都是利用了结构力学方面的特点。这种搜索法比之经典的梯度投影法等似乎来得更有效。这方法效果好，概念也易于为工程人员所接受。

振动设计准则一(同步失效准则):整体结构的最低自振角频率最大值等于各部分结构的最低自振角频率最大值。

振动设计准则二(最优准则): 整体结构的最低自振角频率最大值等于整体结构最低自振角频率对各设计参数函数取最大值。

1.2.2 振动设计的定性判断法

与精确求解的力法和位移法不同，定性判断是未知内力的预测值，要求预测精度越高越好。为了能够定性判断，必须把复杂结构简化成“静定结构”。

确定对应于最低自振角频率的每一单跨梁的振动形式，求出中间零点的位置。就是所求的中间支座放置的位置。

确定附加支座位置，使每跨最低自振角频率数值相等。连续梁的最低自振角频率ωn的数值经常是在每一跨最低自振角频率数值之间，令ωn,1=ωn,2=…。

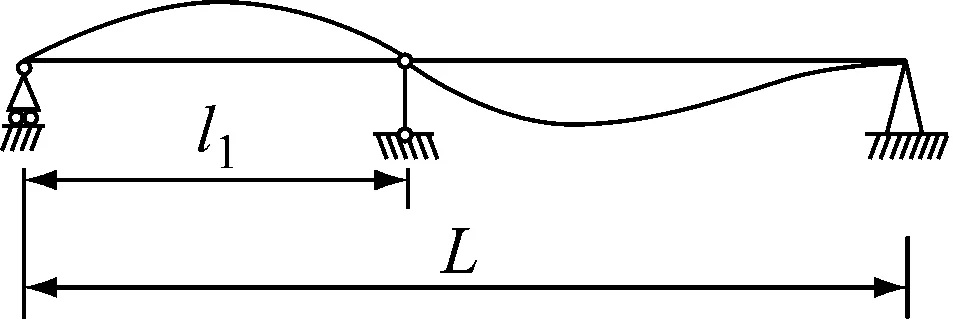
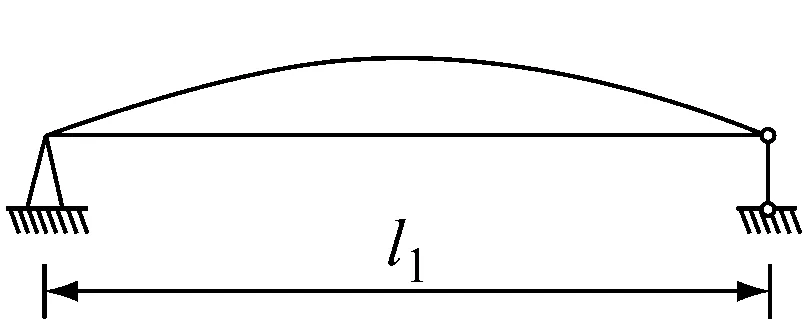
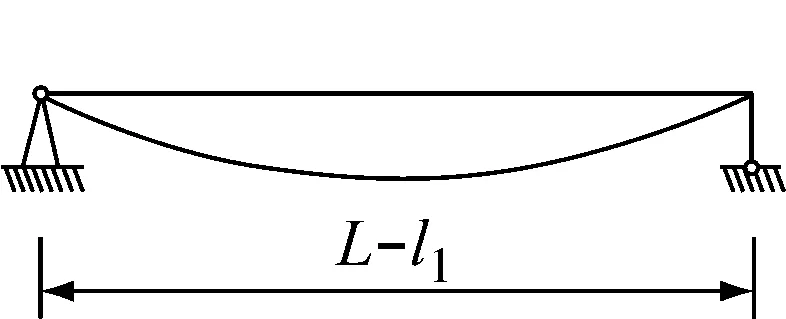
情况一:两端简支，中间有1个可调整支座连续梁，假定反向振动模态，把原来结构分解成两根简支单跨梁(见图2)。

(1)

解得

(a)

(b)

(c)

图2 两端简支中间有1个可调整支座连续梁

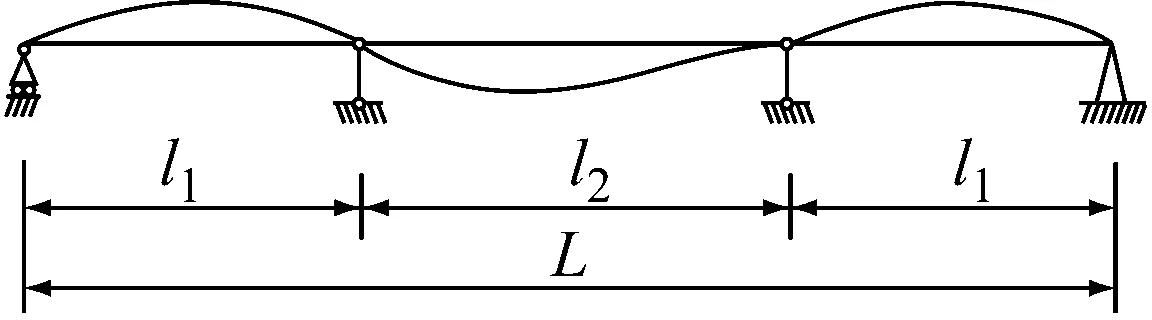
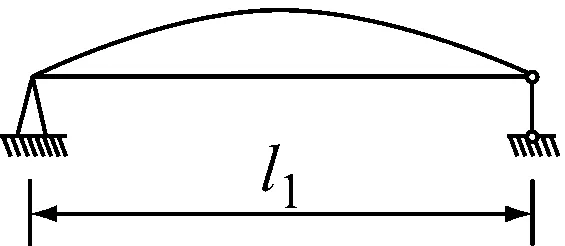
情况二: 两端简支，中间有2个可调整支座连续梁，假定反向振动模态， 把原来结构分解成3根简支单跨梁(见图3)。

(2)解得:

(a)

(b)

(c)

(d)

图3 两端简支中间有2个可调整支座连续梁

推论：两端简支，中间有m个可调整支座连续梁，当各段长度相等时，连续梁具有最低模态固有角频率:

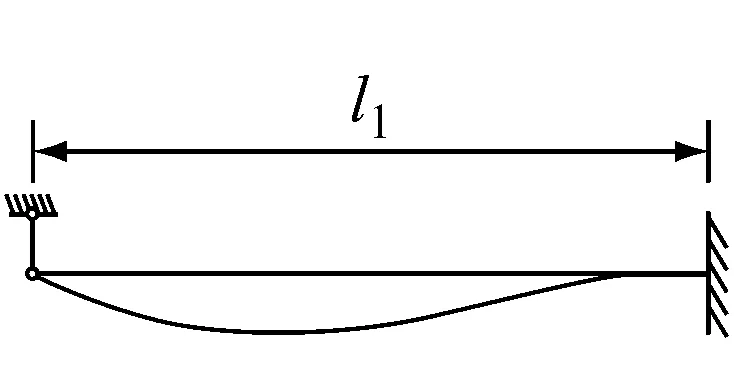
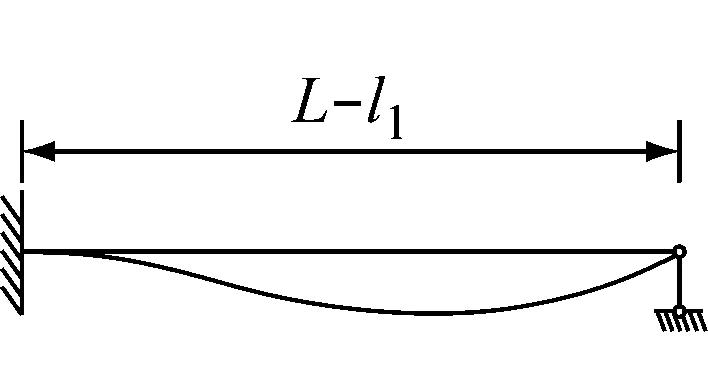
情况三: 两端简支，中间有1个可调整支座连续梁，假定同向振动模态，把原来结构分解成两根一端简支另一端固定单跨梁(见图4)。

(3)

解得:

(a)

(b)

(c)

图4 中间有1个可调整支座

与情况一比较，显然，同向振动模态的固有角频率大于反向振动模态的固有角频率。以下求最低固有角频率采用反向振动模态。

2 有可调支座简支梁固有角频率的快速解析计算

2.1 有1个可调支座时固有角频率的快速解析计算

2.1.1 采用连续分段独立一体化积分法确定最低模态初函数

利用连续分段独立积分法求解步骤(见图5)：

(1) 本题分为两段(n=2)，各段的挠曲线近似微分方程如下:

(4)

(2) 对式(4)各段的挠曲线近似微分方程分别积分4次，得到挠度的通解。在通解中，包含有8个积分常数Ci(i=1,2,…,8)。

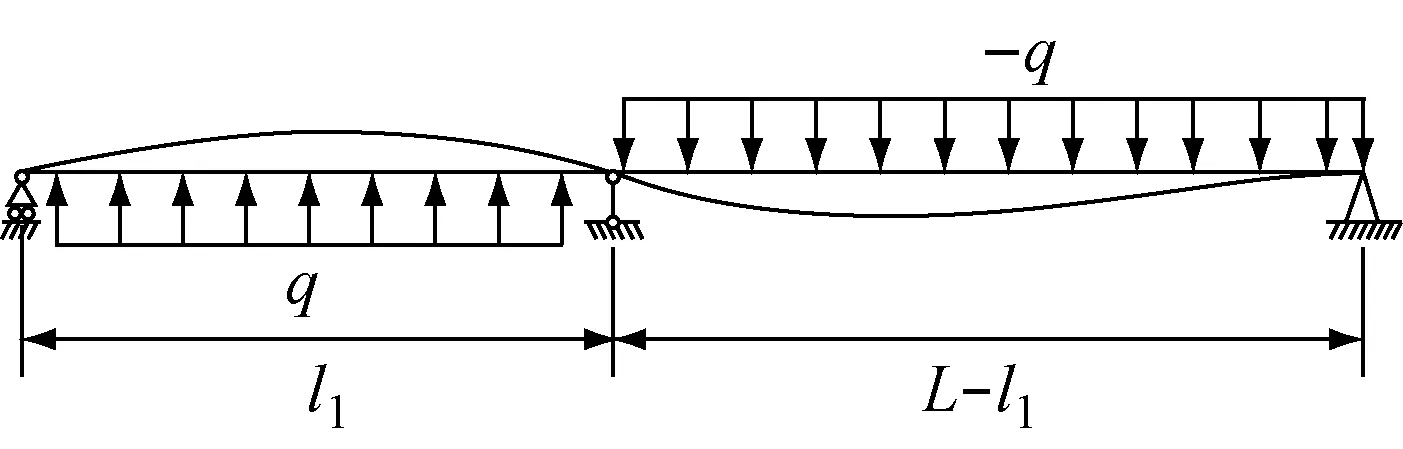
图5 两端简支有1个可调支座连续梁

(振动最低模态初挠度函数采用弯曲-振动比拟)

(3) 利用如下的位移边界条件、力边界条件和连续性条件:

(5)

联立解方程组(5)，得出8个积分常数Ci。

(4) 将Ci代入挠度的通解，得到挠度的解析表达式

(6)

2.1.2 采用最小能量原理确定最低自振角频率一阶近似值

将式(6)确定的初挠度函数代入下式:

(7)得到最小自振角频率关于l1的函数表达式:

连续梁最小自振角频率函数：

梁跨一、跨二最小自振角频率函数分别为：

按振动设计准则一，列方程：

(8)

解得一阶近似同步失效解：

按振动设计准则二，取驻点：

(9)

解得一阶近似最优解：

由图6可见，当l1=l2时，横向自振角频率是最大的；按定性判断法、最小能量法准则一和最小能量法准则二3种解法结果非常接近。

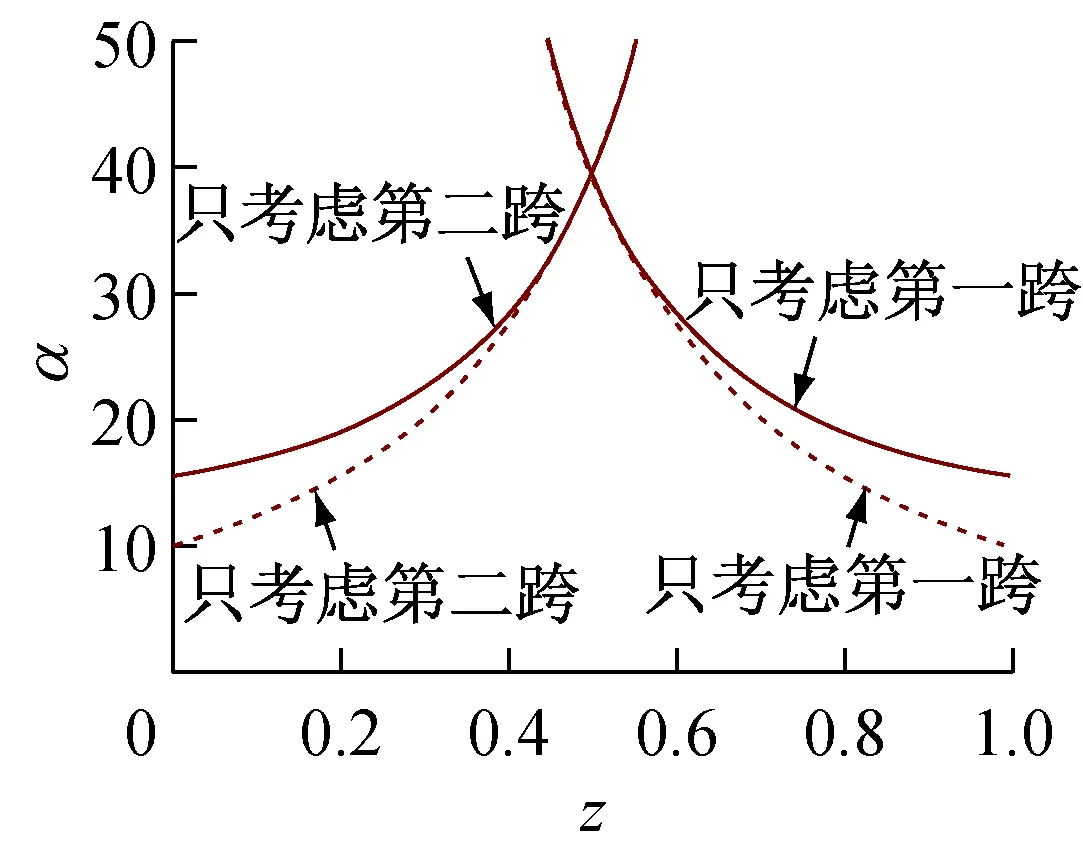
图6 有1个可调支座简支梁固有角频率

…定性判断法，—能量法

2.2 有2个可调支座时固有角频率的快速解析计算

2.2.1 采用连续分段独立一体化积分法确定最低模态初函数

利用连续分段独立积分法求解步骤为(见图7)：

图7 两端简支有2个可调支座连续梁

(振动最低模态初挠度函数采用弯曲-振动比拟)

(1) 本题分为3段(n=3)，各段的挠曲线近似微分方程如下：

(10)

(2) 对式(10)各段的挠曲线近似微分方程分别积分4次，得到挠度的通解。在通解中，包含有12个积分常数Ci(i=1,2,…,12)。

(3) 利用如下的位移边界条件、力边界条件和连续性条件：

(11)

联立解方程组式(11)，得出12个积分常数Ci。

(4) 将Ci代入挠度的通解，得到挠度的解析表达式：

(12)

2.2.2 采用最小能量原理确定最低固有角频率一阶近似值

将式(12)确定的初挠度函数代入下式：

(13)

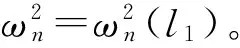
按稳定性设计准则一，列方程：

(14)

解得一阶近似同步失效解：

按振动设计准则二，取驻点：

(15)

解得一阶近似最优解：

由图8可见，当l1=l2时，横向自振角频率是最大的；按定性判断法、最小能量法准则一和最小能量法准则二3种解法结果非常接近。

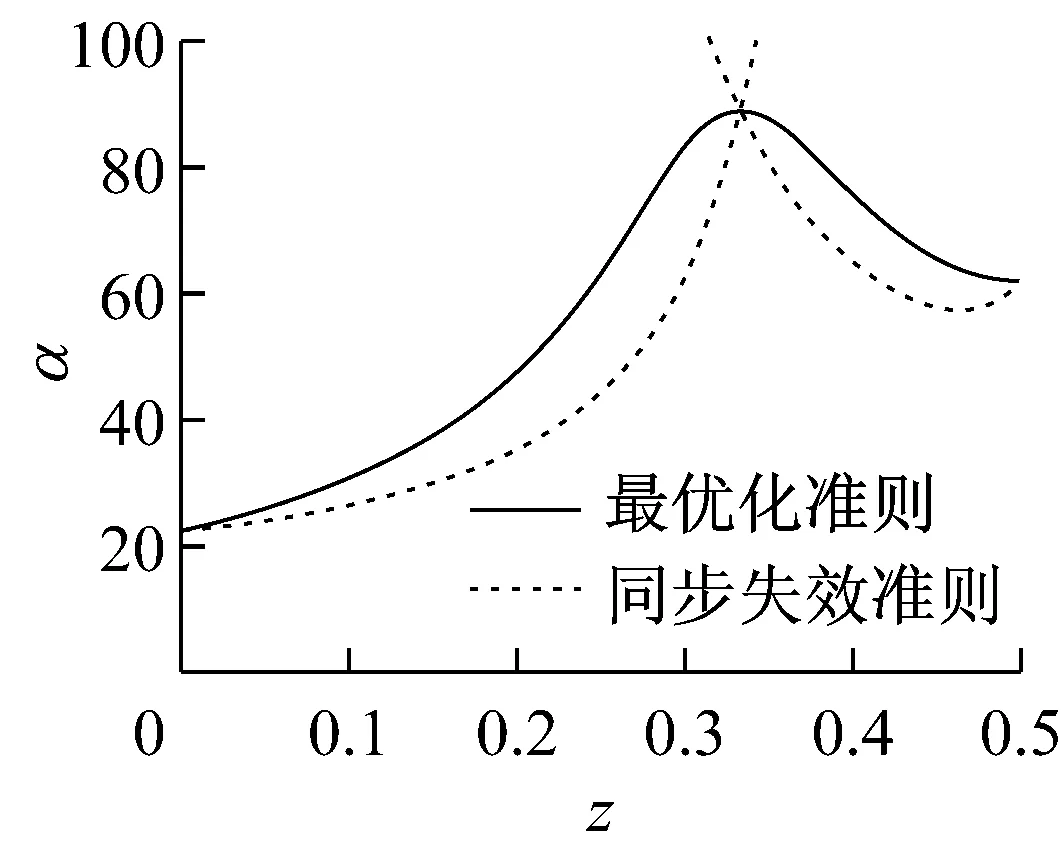
图8 2个可调支座简支梁固有角频率

3 一端简支一端固定可调中间支座连续梁的最低固有角频率

3.1 最低固有角频率的一阶近似解析解

3.1.1 连续分段独立一体化积分法确定最低振动模态函数

利用连续分段独立积分法求解步骤为(见图9)：

(1) 本题分为两段(n=2)，各段的挠曲线近似微分方程如下：

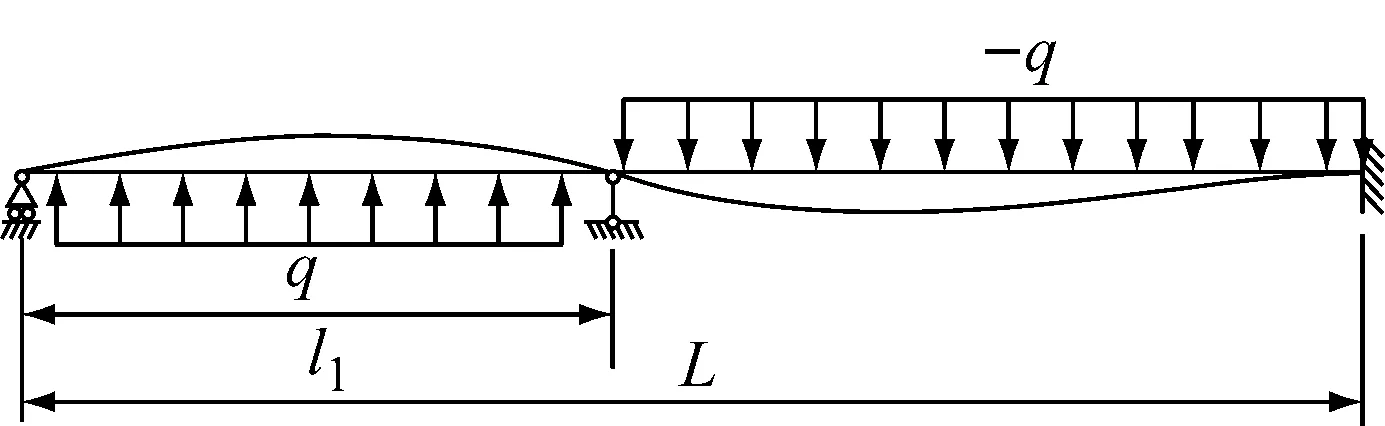
图9 一端简支另一端固定有1个可调支座连续梁

(振动最低模态初挠度函数采用弯曲-振动比拟)

(16)

(2) 对式(16)各段的挠曲线近似微分方程分别积分4次，得到挠度的通解。通解中，包含有8个积分常数Ci(i=1,2,…,8)。

(3) 利用如下的位移边界条件、力边界条件和连续性条件：

(17)

联立解方程组(17)，得出8个积分常数Ci。

(4) 将Ci代入挠度的通解得到挠度的解析表达式：

(18)

3.1.2 采用最小能量原理确定最低固有角频率一阶近似解析解

将式(18)确定的初挠度函数代入式(7)，得到最低固有角频率关于l1的函数表达式：

按振动设计准则一，列方程：

(19)

解得一阶近似同步失效解：

按振动设计准则二，取驻点：

(20)

解得一阶近似最优解：

结果表明：采用最小能量法计算按同步失效准则和最优化准则得到的最低固有角频率结果不一致，但比较接近。

3.2 最低自振角频率的精确解析解

3.2.1 渐近法确定最低振动模态函数

将振动中性平衡的微分方程式：

(21)

取式(18)的挠度作为初函数v1,[0]，v2,[0]则：

(22)

将式(22)积分4次得到v1,[1]，v2,[1]的通解，此时之边界条件仍为式(17),利用式(17)确定积分常数，就得到v1,[1]，v2,[1]的解析表达式，依次逐步迭代就可得到v1,[n]，v2,[n](n=1,2,…)的解析表达式。

3.2.2 采用最小能量原理确定最低固有角频率精确解析解

将挠度函数v1,[n]，v2,[n](n=1,2,…)的解析表达式代入式(7)，得到最低固有角频率关于l1的函数表达式ωn=ωn(l1)，其中z=l1/L。

按振动设计准则一，列方程：

(23)

解得精确同步失效解：

按振动设计准则二，取驻点：

(24)

解得精确的最优解：

图10给出了一端简支一端固定可调中间支座连续梁的最低固有角频率按最优化准则渐近法迭代次数的比较，计算结果非常接近。

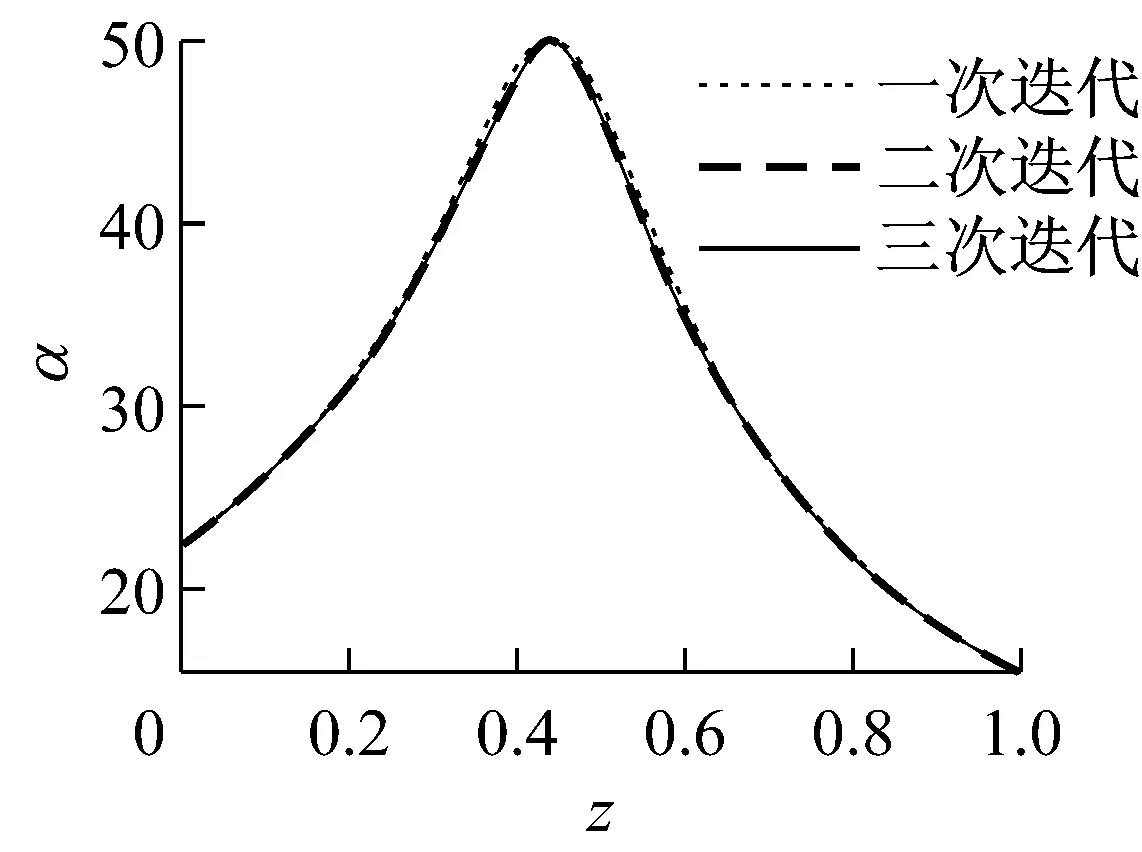
图10 一端简支一端固定可调中间支座连续梁的最低固有

角频率按最优化准则(渐近法迭代次数比较)

4 结果分析

表1给出了4种方法的连续梁调整最低固有角频率计算结果，表中：

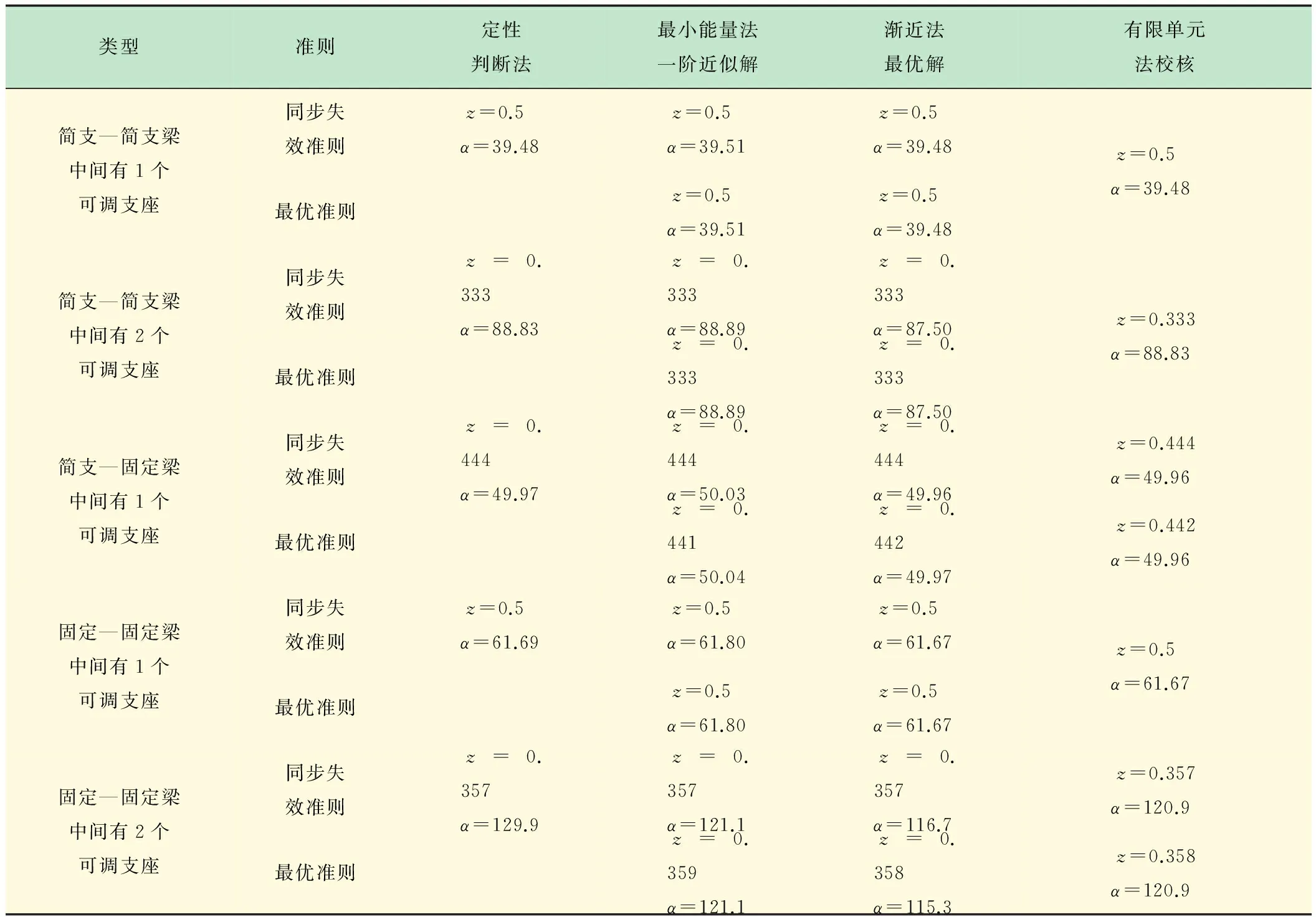
表1 连续梁振动调整各种计算方法最低自振角频率对比表

由表1可以看出：①定性判断法虽然不能得到最优解，但可以得到接近最优解的同步失效解；②最小能量法一阶近似解虽然有一定误差但可以得到简单的解析表达式供工程设计参考；③渐近法可以得到最优解，一般迭代2,3次就可以得到精确解(见图10)；④有限单元法可以得到精确的数值解，但不能得到解析表达式；⑤同步失效准则与最优准则计算结果接近。

5 结 语

本文从力学模型研究入手，建立了一种连续梁振动求解的通用模型，推导出连续梁振动模态计算的一般方程和程序化求解的通用程序。利用连续分段独立一体化积分法求解可以得到最低固有角频率的解析解，求解过程简洁方便、快速准确，适用于各种边界条件的连续梁最低固有角频率计算。

基于弯曲-振动比拟法采用连续分段独立一体化积分法求得振动初模态解析挠度函数，与最小能量法相结合求解了结构振动调整的一阶近似最低固有角频率解析表达式；进而基于精确的梁振动微分方程采用渐近法积分得到梁振动模态解析挠度函数，与最小能量法相结合求解了结构振动调整的最优固有角频率解析表达式。

推广“连续分段独立一体化积分法”在振动工程中的应用，具有重要的理论意义和工程实用价值。

[1] 李银山，陈予恕，吴志强．正交各向异性圆板非线性振动的亚谐分岔[J].机械强度，2001, 23(2): 148-151.

[2] 李银山，杨桂通, 张善元，等.圆板受迫振动超谐分岔和混沌运动的实验研究[J].实验力学，2001，16(4)：347-358.

[3] 李银山，陈予恕，李伟锋．各种板边条件下大挠度圆板的全局分岔和混沌[J].天津大学学报，2001，34(6)：718-722.

[4] 李银山，刘 波，龙运佳，等．二次非线性粘弹性圆板的2/1+3/1超谐解[J].应用力学学报，2002，19(3)：20-24.

[5] 李银山，高 峰，张善元，等．二次非线性圆板的1/2亚谐解[J].机械强度，2002，24(4)：505-509.

[6] LI Yin-shan，Zhang Nian-mei，YANG Gui-tong．1/3 Subharmonic solution of elliptical sandwich plates[J].Applied Mathematics and Mechanics，2003，24(10)：1147-1157.

[7] 李银山，李欣业，刘 波，等．二次非线性粘弹性圆板的2/1超谐解[J].工程力学，2003，20(4)：74-77.

[8] 李银山，刘世平，蔡中民，等．框架剪力墙高层建筑结构抗震优化设计[C]//力学与工程应用. 北京：中国林业出版社，1996：380-383.

[9] 刘世平，李银山，解可新，等．剪切型多层钢框架抗震优化设计[J].天津大学学报， 1997，30(4)：517- 522.

[10] 李银山．材料力学(下册)[M]，北京：人民交通出版社， 2014.

[11] 李银山，徐秉业, 李树杰．基于计算机求解弯曲变形问题的一种解析法(一)——复杂载荷作用下的静定梁问题 [J] ．力学与实践，2013：35(2)：83-85.

[12] 吴艳艳，李银山，魏剑伟，等．求解超静定梁的分段独立一体化积分法[J].工程力学，2013,30(增刊):11-14.

[13] 李银山，李 彤，郭晓欢，等.索-梁耦合超静定结构的一种快速解析法[J]．工程力学，2014，31(增刊)：11-16.

[14] 李银山，官云龙，李 彤，等.求解变截面梁变形的快速解析法[J]．工程力学，2015，32(增刊)：116-121.

[15] 李 彤，李银山，霍树浩,等. 杆件体系稳定性调整的快速解析研究[J]．起重运输机械，2015(9)：36-42.

Study on a Fast Analytical Method of Adjustment of Continuous Beam Vibration

LITong1，LIYin-shan2，HUOShu-hao3，WEIBing-wei2

(1．Key Laboratory of Pressure Systems and Safety, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China; 2． School of Mechanical Enginearing， Hebei University of Technology, Tianjin 300130， China; 3． School of Mechanics Eng.， Taiyuan University of Science & Technology, Taiyuan 030024， China)

A continuous subsection independently systematic integral method (CSISIM) is used to solve the analytical expressions of the natural angular frequency of continuous beams vibration. First the forth-order differential deflection equations are derived by bending-vibration analogy method. Then the general solutions of beam deflection are obtained by independent forth-fold integration. Integral constants are determined by boundary conditions and continuity conditions to determine the analytical solution of deflection. According to the principle of minimum energy, we get the first order approximate analytical solution of the natural angular frequency. Then by progressive method, more accurate analytical solution is obtained by solving exact differential equations of the vibration. According to the principle of minimum energy, the exact expression of natural angular frequency can be solved. The support position of the continuous beam is adjusted by simultaneous failure criterion and optimization criterion of vibration structure. Analytic expression of the optimal solution of the nature angular frequency of the structure is obtained. The changing curve of the natural angular frequency versus position is plotted. The engineering example shows the CSISIM method is a general method suitable for computer stylized programming to solve. It can obtain the optimum analytical solution of natural angular frequency.

vibration adjustment; natural angular frequency; fast analysis method; minimum energy principle; progressive method

2015-08-31

国家自然科学基金资助项目(10632040)

李 彤(1962-)，女，浙江绍兴人，博士，讲师，主要从事结构优化设计研究。Tel.：021-64253308;E-mail: tongli@ecust.edu.cn

TU 311.41

A

1006-7167(2016)05-0004-06