永磁同步电动机的哈密顿最优控制系统
徐建英,谷伟志,吴 婷
(辽宁科技大学,鞍山 114051)
永磁同步电动机的哈密顿最优控制系统
徐建英,谷伟志,吴 婷
(辽宁科技大学,鞍山 114051)
针对内埋式永磁同步电动机数学模型的非线性,基于非线性系统正交分解的端口受控哈密顿模型,采用能量成型与无源性的控制方法,设计了内埋式永磁同步电动机调速系统的控制器,并证明了该系统的稳定性。将速度控制问题转化为带阻尼系数的一阶微分方程求解问题,给出了阻尼系数的求取方法。进而提出了同时考虑逆变器电压约束和最大转矩/电流比控制的优化方法,为哈密顿控制器提供了期望平衡点。仿真结果表明该调速系统具有良好的控制性能。
非线性模型;端口受控哈密顿模型;逆变器约束;最优化
0 引 言
内埋式永磁同步电动机(以下简称IPMSM)近年来获得了广泛的应用,由于IPMSM的逆凸极性,其数学模型具有非线性、强耦合特点,因而诸多非线性控制方法[1-5]被应用于IPMSM的转速控制系统,如微分几何法、逆系统法、非线性自适应法等,这些方法多采用线性化拟合技术,在弱磁控制方面研究较少。
文献[1-2]提出了基于互联阻尼配置方法(interconnection and damping assignment passivity based control,IDA-PBC)的哈密顿控制器,从能量的角度对永磁同步电动机建立端口受控哈密顿结构模型,(port-controlled Hamiltonian,PCH),通过加入反馈函数,构造可作为Lyapunov的能量存储函数,设计控制器,在中低速范围内有良好的调速性能。文献[3]提出了由哈密顿雅可比方程式设计的无源控制器,采用这种方法可以更加简便地设计控制器,对阻尼系数合理设置后,具有良好的调速性能。但上述两种方法中系统的平衡点需要根据不同控制方法进行计算,无法实现算法的平滑切换,故难以实现无扰动的全范围调速。文献[4]提出了考虑逆变器电压约束的哈密顿控制器,使用泊松定理将端口受控哈密顿模型扩展到广义领域,设计了使用查表法的控制器,该控制器在低速区内调速性能良好。同时,文献[5]划定了弱磁区域给出了基于梯度下降法的弱磁运行曲线,使得电机能够在低、中、高转速区域切换,但该方法计算量较大,算法编程不宜实现[6-9]。
本文提出了一种平衡点可调的哈密顿控制器,同时给出考虑逆变器电压约束的MTPA电机运行曲线,为哈密顿控制器提供实时运行的最优平衡点,使得电机能够全速度范围无扰动切换,对突加负载扰动有较强的抑制作用。
1 IPMSM的PCH建模
端口受控哈密顿系统的标准形式[10]:
(1)
令:R(x)=g(x)KgT(x),则反馈率可写作u=-Ky,其中K=KT≥0。
由坐标变换理论可知,IPMSM在dq轴上的模型[11-12]:
(2)
式中:ud,uq为定子dq轴电压;,id,iq为定子dq轴电流;ω为转子的机械角速度;p为转子极对数;Ld,Lq为定子dq轴电感;Te,TL分别为电磁转矩和负载转矩;R为定子电阻;J为转动惯量;φ为永磁体磁通,忽略摩擦系数。
将系统的状态x、输入u、输出y分别定义如下:
(3)
哈密顿函数为系统的电能与机械能综合,取哈密顿函数:
(4)
由此可推导出形如式(1)的PCH:
(5)
(6)
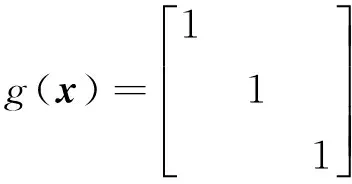
(7)
2 IPMSM无源控制器设计
2.1PCH的控制器设计原理

(8)
中,则系统渐近稳定。
加入阻尼能够使系统稳定在自身固有的平衡点上,为了将系统稳定在期望的平衡点附近,需要构造系统能量函数:
(9)
式中:Ha(x)表示由控制注入系统的能量,为待定函数。此时反馈率:
u=-Ky+v
(10)
设v为系统的新输入,若v满足偏微分方程:
(11)
且Ha(x)满足:
(12)
(13)
则x*为闭环系统的渐近平衡点。
2.2 IPMSM的系统控制器设计
(14)
则哈密顿函数H(x)可取:
(15)
显然,Ha(x)满足式(13)条件,x*为系统的一个渐近稳定平衡点。
仍取控制率如式(10)形式,则由式(11)可得:
(16)
(17)
将式(7)、式(16)、式(17)代入式(10)可得电机控制器的方程:
由式(8)可推得系统的最大吸引域:
由式(19)可为阻尼系数r1,r2,r3的选取给出指导范围。r3越大,则系统对速度变化的控制越明显,r1,r2的大小分别代表了期望的id,iq作用效果比重。
已知在初始状态下,ids,iqs,ωs均为0,则最大吸引域:
(20)
令:
(21)
(22)
(23)
由式(21)、式(22)可知,以α1,α2建立直角坐标系,α1为id的函数,α2为iq的函数。令α3垂直于α1,α2平面,则式(23)位于空间平面α1+α2=-α3上,将其投影到α1,α2平面可得到二维坐标系下的吸引域。
由图1可知,区域D为吸引域。显然,当r1,r2,r3增大时,区域D相应缩小,系统能够更快的趋近于平衡点,但区域D缩小将会导致系统稳定裕度变差。
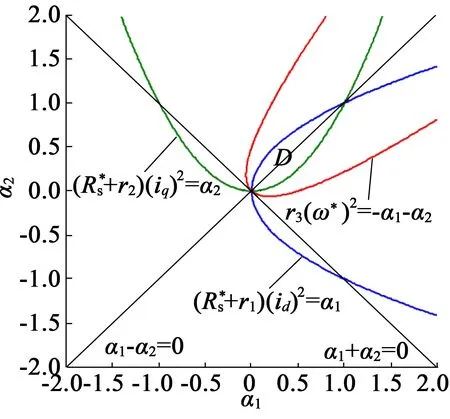
图1 控制器在二维坐标系下的吸引域

3 IPMSM控制器最优化设计
3.1 系统平衡点最优化
由式(18)可知,IPMSM的无源控制器中已包含q轴电流的期望平衡点,根据IDA-PBC原理设计的无源控制器解决了永磁同步电动机模型非线性的问题,通过合理配置吸引域,即可实现IPMSM的非线性控制器设计。但考虑到逆变器存在电压约束问题和对调速系统全范围调速性能的要求,传统的id=0控制方法难以满足需要,故需要设计一种考虑逆变器电压约束和最优id电流的控制器。
最大转矩/电流比(MTPA)控制能够在给定转矩的情况下,最优配置交直轴电流分量,使定子电流最小,达到单位电流下电机输出转矩最大。由于逆变器的容量是一定的,采用最大转矩电流比控制,可以使逆变器所需输出电流较小,减小IPMSM对逆变器的容量要求[6-9]。
由式(2)中运动方程式可推得:
(24)

(25)
由此可推出:
(26)
显然,id与iq的计算非常复杂,由文献[10-12]可知,通常采用MATLAB拟合曲线的方式给出id(Te)与iq(Te)两条曲线,由此实现电机MTPA控制。但MTPA控制并没有考虑逆变器电压约束问题,即:
(27)
(28)
(29)
式(29)为固定电压下id与iq的关系。由式(26)、式(27)、式(29)给出IPMSM运行过程中的电流、电压轨迹,如图1所示。
由图2可知,当电机在A点运行时,已经达到iq的最大值,继续按照MTPA曲线运行,只能使得电机状态向A4方向运行,iq电流工作在极限处,而不能保证电机输出转矩最大。由式(28)可知,iq决定了ud的大小,当式(27)成立时,由式(29)可推出极限电压下的最优id电流:
(30)
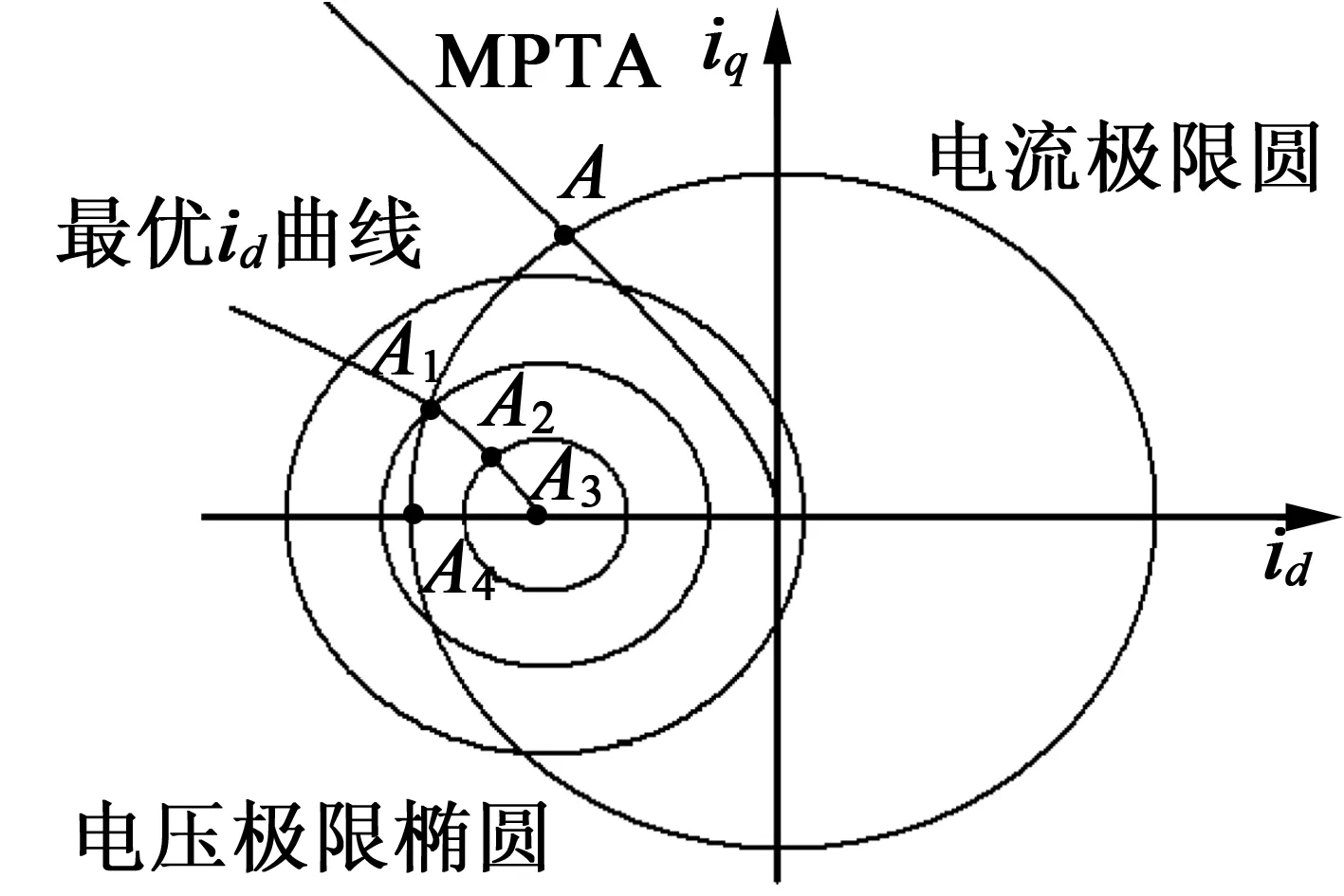
图2 IPMSM运行状态
由式(30),当电机运行在A点状态后,会沿着电流极限圆运行至A1并继续由A1向A2,A3运行。由式(24)、式(25)易知,此时输出转矩最大。
3.2 IPMSM的哈密顿最优控制器
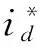
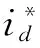
(31)
由式(18)、式(27)可得到最优无源控制器。哈密顿最优控制系统如图3所示。
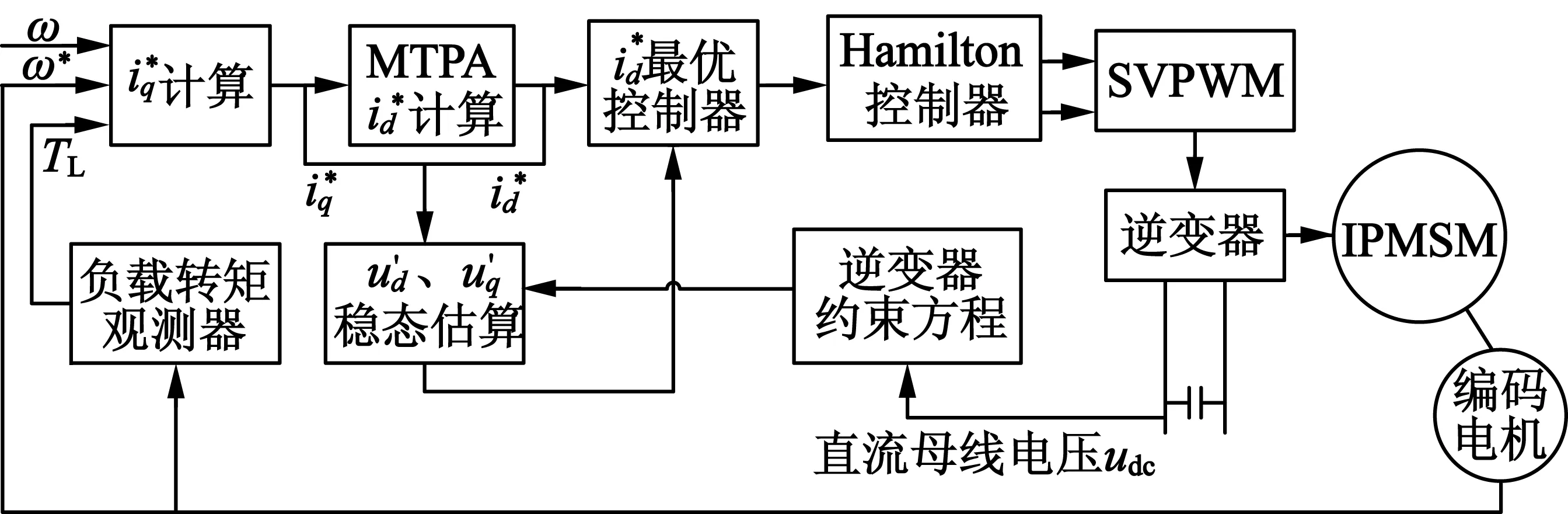
图3 哈密顿最优控制器系统框图
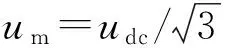
4 仿真试验
在MATLAB/Simulink环境下搭建仿真模型对系统进行仿真。IPMSM的参数:额定电压220 V,额定功率1.1 kW,额定转矩5.8 N·m,额定转速为1 800 r/min,转动惯量J=0.000 8 kg·m2,极对数p为2,永磁体磁通φ为0.225 Wb,定子电阻为1.187 5 Ω,d轴等效定子电感Ld为0.006 H,q轴等效定子电感Lq为0.008 H。由图1选择阻尼系数为r1=8,r2=8,r3=9。
为了验证系统的全范围调速性能,在t=0,t=0.02 s,t=0.04 s,t=0.06 s时分别给定机械角速度ω为500rad/s,1500rad/s,3000rad/s,1000rad/s。
由图4可知,采用哈密顿最优控制器后,IPMSM能够在全范围调速,且转速无超调,拥有良好的加减速性能。在由1 500rad/s基频以下速度范围向3 000rad/s基频以上调速范围切换时,系统可以实现无扰动平滑切换。
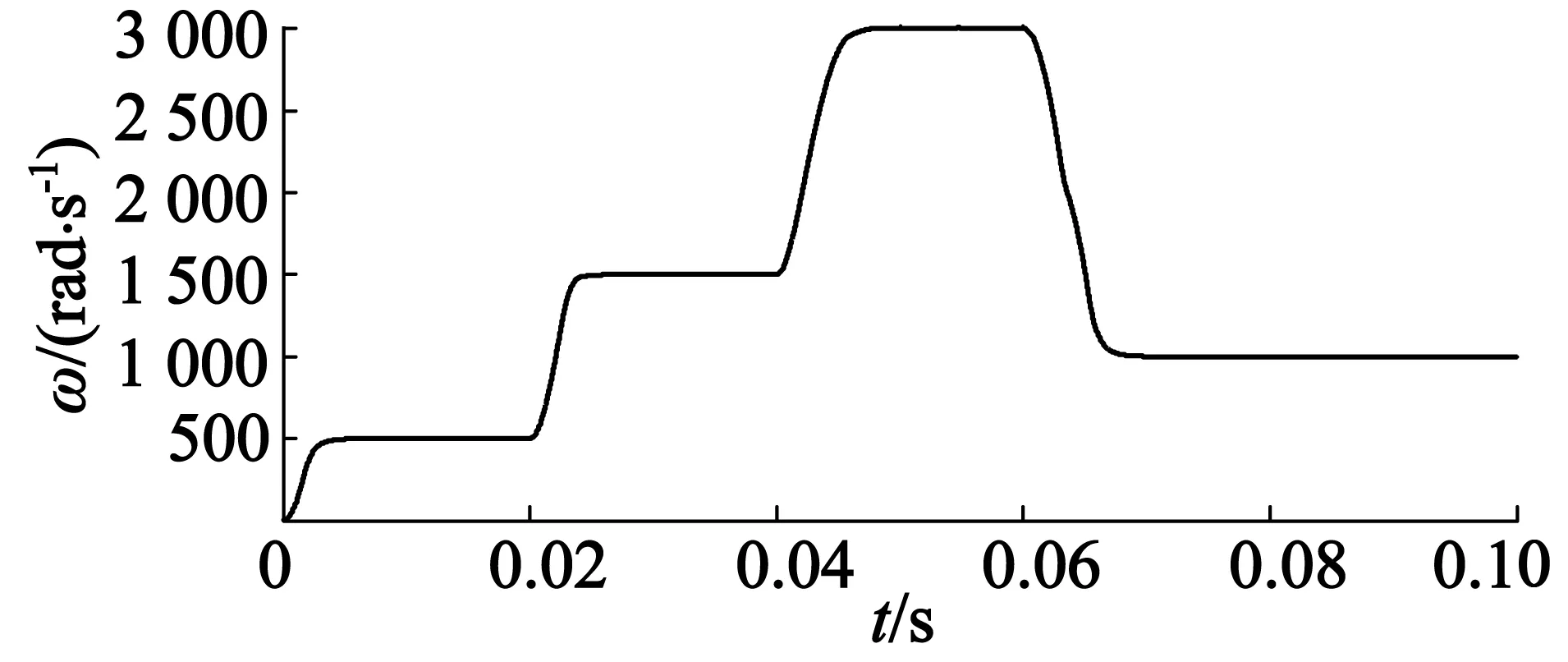
图4 IPMSM的全范围调速曲线
设定系统的机械角速度为500rad/s,在0.05s时突加10N·m负载,并将使用哈密顿控制器的传统MTPA控制器与最优无源控制器相比较,由图5可知,最优控制器的转速降明显小于MTPA无源控制器,且在0.065s后即恢复稳态。
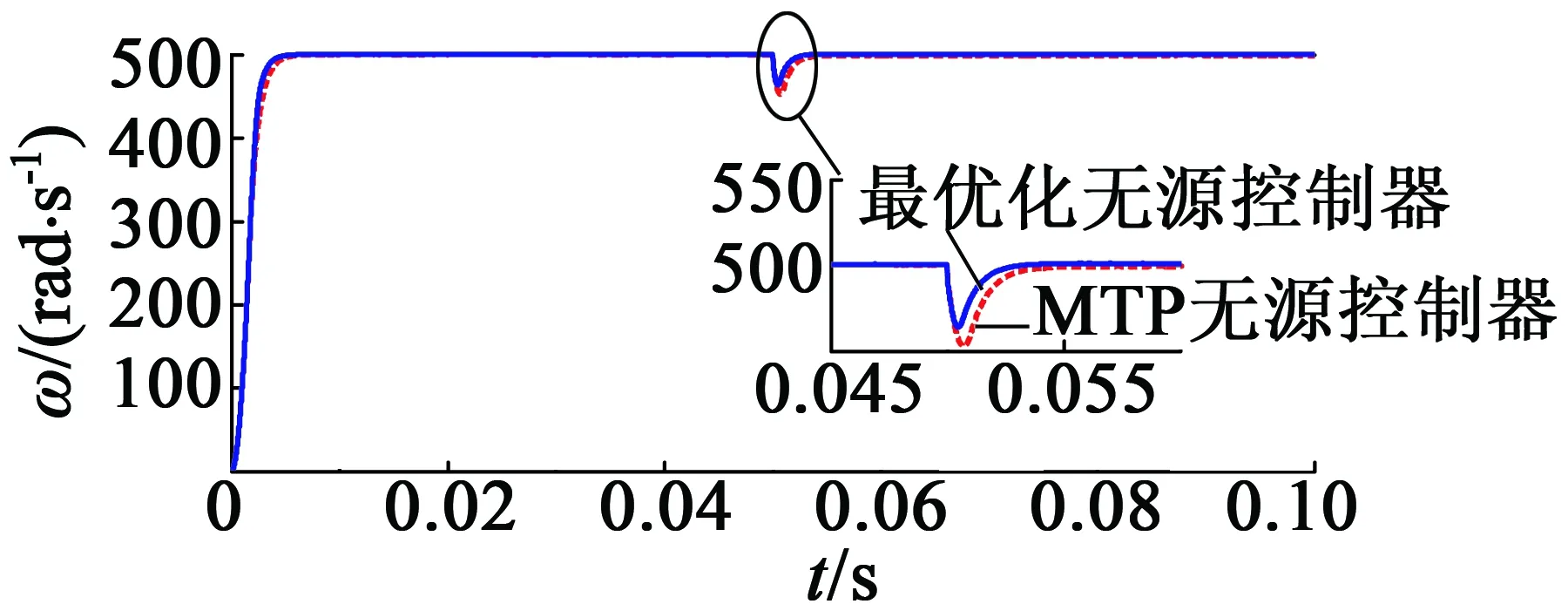
图5 IPMSM低速运行曲线
在1 500rad/s机械角速度下,同样在0.05s加入10N·m负载,由图6可知,此时采用最优无源控制器的系统性能优于传统MTPA无源控制器。
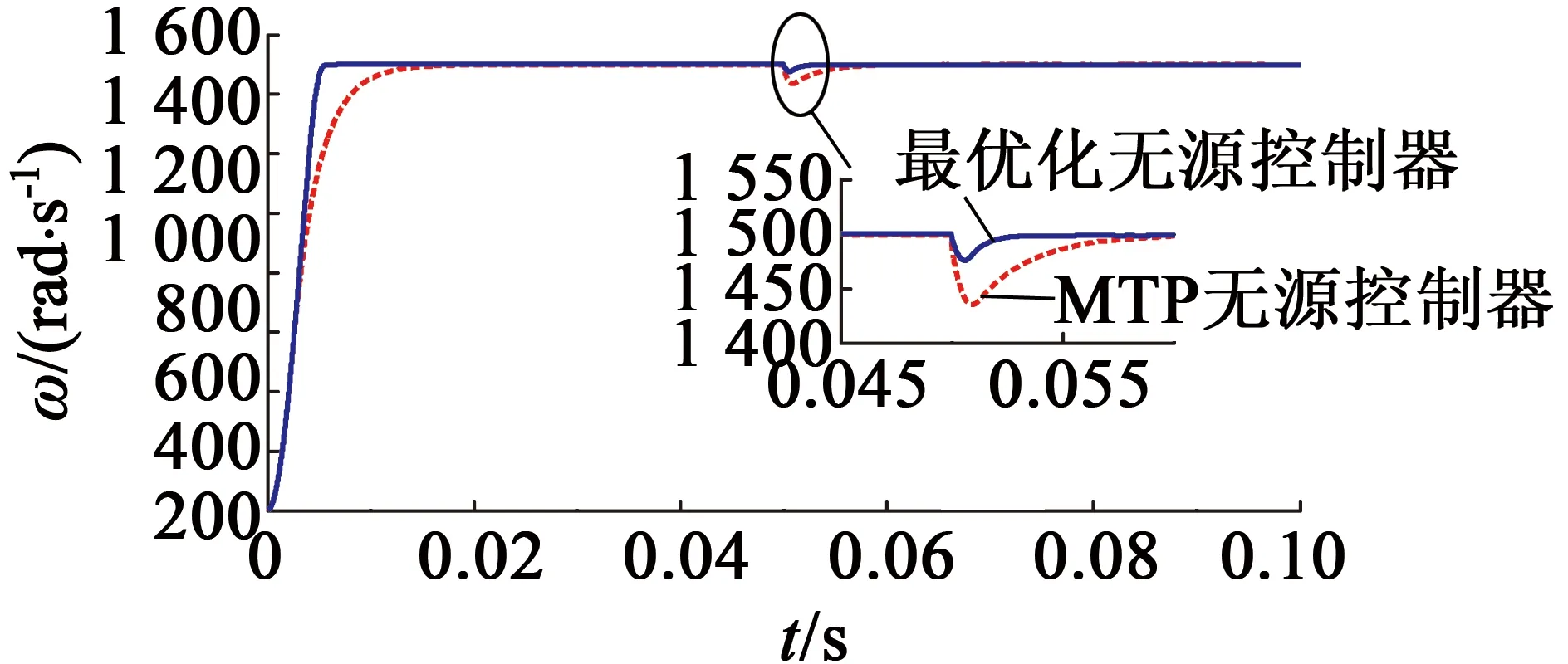
图6 IPMSM额定转速运行曲线
在机械角速度2 500rad/s条件下重复试验,由图7可知,在弱磁恒功率调速范围内,最优无源控制器起动速度与抗扰动能力明显优于传统MTPA无源控制器。
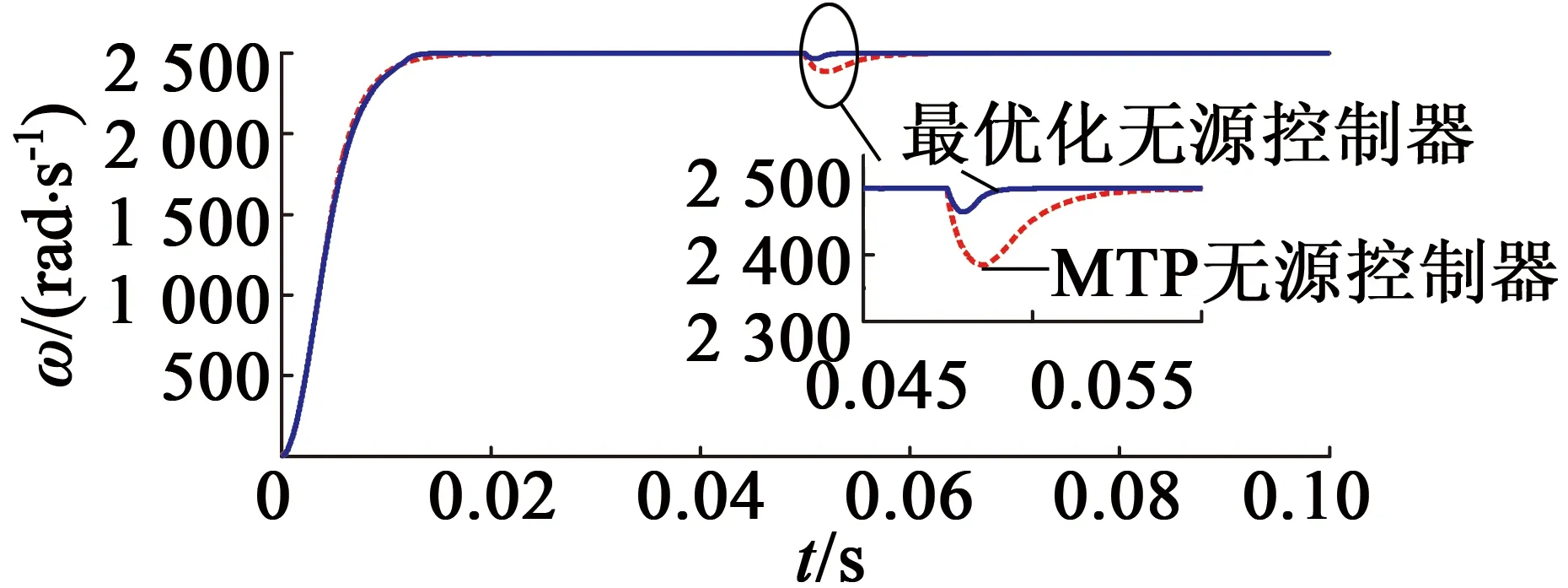
图7 IPMSM高速运行曲线
在初始机械角速度ω为1 500rad/s,0.05s突加10N·m负载的情况下,IPMSM的电磁转矩、dq轴、ABC相电流曲线分别如图8~图10所示。
由图8可知,电磁转矩平稳,无明显脉动,0.05s突加负载后,能够快速地调节并输出相应电磁转矩。图9中电机定子d轴电流始终处在弱磁状态;q轴定子电流,在突加负载后增加,而d轴电流无明显改变,保证系统工作在MTPA的最大转矩/电流比状态。由图10,SVPWM输出三相电流波形良好,在0.05s突加负载后,波形未发生明显变化,说明系统具有良好的抗扰动特性。
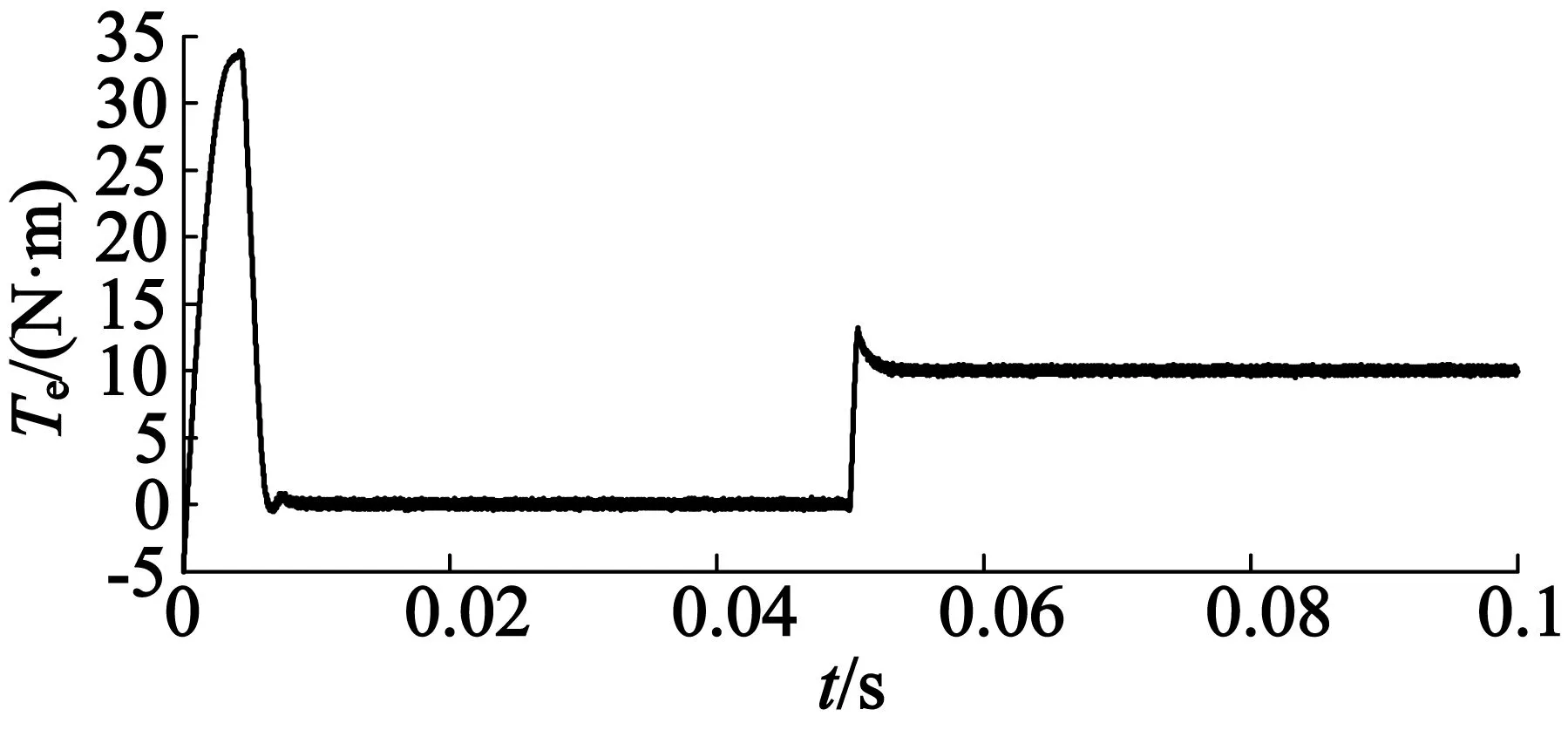
图8 IPMSM电磁转矩曲线
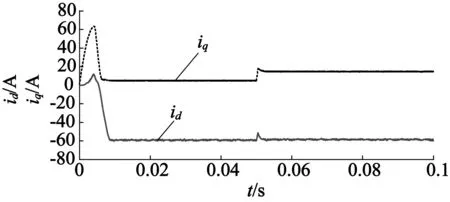
图9 IPMSM的dq轴电流曲线
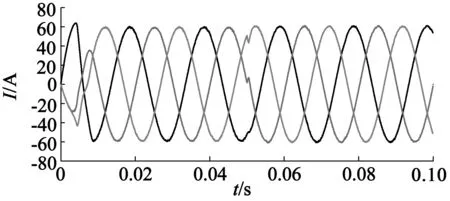
图10 IPMSM额定转速下三相电流
5 结 语
[1] 何朕,邵明,孟范伟,等.哈密尔顿系统的无源性控制设计[J]. 电机与控制学报,2008,12(9):571-575.
[2] 裘君,赵光宙,齐冬莲.PMSM的哈密顿反馈耗散增益调度控制[J].控制工程,2010,17(2):152-153.
[3]YEMEMURAY,SAKAMOTON.NonlineroptimalservocontroldesignforPMSMwithinvertervoltagenormconstraints[J].TransactionsoftheInstituteofSystems,ControlandInformationEngineers,2013,26(7):252-260.
[4]SAKAMOTON,VANDERSCHAFTAJ,AnalyticalapproximationmethodsforthestabilizingsolutionoftheHamilton-Jacobiequation[C].IEEETrans.onAutomat.Contr. ,2008,53(10):2335-2350.
[5] 盛义发,喻寿益,桂卫华,等.轨道车辆用永磁同步电动机系统弱磁控制策略[J].中国电机工程学报,2010,30(9):74-79.
[6] 孙旭霞,岳经凯.永磁同步电动机MTPA弱磁控制方法研究[J].电气传动,2012,42(11):62-64.
[7] 冷再兴,马志源.一种新的内置式永磁同步电动机弱磁调速控制方法[J].微电机,2006,39(6):11-14.
[8]SAKAMOTON.Casestudiesontheapplicationofthestablemanifoldapproachfornonlinearoptimalcontroldesign[J].Automatica, 2013,49(3):568-576.
[9] 徐建英, 刘贺平.PMSM的高精度感应电势状态观测器[J]. 北京科技大学学报, 2007,29(5):538-539.
[10] 史宇超,孙凯,黄立培,等.内埋式永磁同步电动机宽调速范围运行策略[J].清华大学学报:自然科学版,2012,52(11):1565-1570.
[11]FUJIMOTOR,SAKAMOTON.Thestablemanifoldapproachforoptimalswingupandstabilizationofaninvertedpendulumwithinputsaturation[C]//Proc.ofthe18thIFACWorldCongress,2011:8046-8051.
[12] 张朝阳,冯晓云.永磁同步电动机弱磁运行控制策略研究[J].电气传动,2014,44(5):40-43.
Optimal Control of Hamiltonian System of Permanent Magnet Synchronous Motor
XUJian-ying,GUWei-zhi,WUTing
(University of Science and Technology Liaoning,Anshan 114051,China)
To nonlinear characteristics of the mathematical model of interior permanent magnet synchronius motor (IPMSM), a controller of the speed control system was proposed based on the port-controlled Hamiltonian (PCH) of orthogonal decomposition of nonlinear systems, using the method of interconnection and damping assignment passivity based control (IDA-PBC). It is proved that the system is stable. A method to obtain damping coefficient was given with that turn the speed control problems into the solving it for first order differential equations with damping coefficient. Then an optimization method was presented that at the same time to consider constraint voltage of the inverter and maximum torque per ampere (MTPA) of the IPMSM, to provide expectations of equilibrium point for Hamilton controller. Simulation results show that the system has good control performance.
nonlinear model; port-controlled Hamiltonian (PCH); constraints of the inverter; optimization
2015-06-18
国家科技支撑计划项目(2014BAB02B01)
TM341;TM351
A
1004-7018(2016)01-0043-05
徐建英(1961-),男,博士,教授。

