纯电动汽车用永磁同步电机温度场计算

李东和

(辽宁省交通高等专科学校，沈阳 110122)



纯电动汽车用永磁同步电机温度场计算

李东和

(辽宁省交通高等专科学校，沈阳 110122)

以一台额定功率为25 kW的纯电动汽车用永磁同步电机为研究对象，利用集中参数法建立了电机的热网络模型，通过建立其热平衡方程组，计算电机内各零部件的节点温度；同时基于有限体积法，建立了电机的求解域模型，利用Fluent软件计算电机的温度场，并同热网络法求解进行比较。借助于实验平台，对计算结果和实验结果进行对比分析，以验证利用热网络法和有限体积法求解电机温度场的准确性。

永磁同步电机；温度场；热网络；有限体积法

0 引 言

随着能源需求的改变，纯电动汽车[1]逐渐成为汽车市场上有力的竞争者。纯电动汽车的工作是以电能为输入源，通过电驱动系统[2]驱动整车运行。因此，电驱动系统的有效工作是保证纯电动汽车正常行驶的必要条件。永磁同步电机[3]作为电驱动系统的核心部件，在工作过程中必须具备可靠性和有效性条件。当电能驱动电机工作时，由于电机内电磁效应和机械转动导致电机温度升高，而电机温度过高时，直接影响绕组绝缘性能和永磁体物理性能，进而降低了电机的可靠性和寿命。因此，对纯电动汽车用永磁同步电机的温度场研究具有重要的意义。

现阶段，电机温度场的研究方法主要有等效热路法、等效热网络法、有限元法和有限体积法。等效热路法一般用于求解电机内各部分的平均温度，文献[4]介绍了基于等效热路法求解的基本原理，利用MOTOR-CAD求解电机温度场；等效热网络法可通过建立多节点模型以研究目标的温度场，文献[5-6]是通过建立电机的热网络模型，求解电机各内节点的温度；有限元法能够较准确地计算电机温度场，得到电机内各部分的温度，但对于液冷电机中流体和固体耦合场的计算欠缺条件，文献[7]通过有限元方法计算出电机内温度分布，并说明了多种因素对电机散热的影响；有限体积法是基于流固耦合的基本理论，能够精确地计算液冷电机内的温度场和流体场，文献[8-9]基于有限体积法，通过CFD软件精确计算了电机内各部分的温升。

在满足精度要求的条件下，利用热网络法能够快速计算电机热网络中的节点温度，确定电机内的温度分布，缩短设计周期；同时利用有限体积法计算电机的温度场时，有限体积法能够较好地进行流固耦合场的计算，准确反映电机内各部分的温度分布和温升特性，但仿真周期较热网络法长。因此，在设计电机阶段和后续验证阶段，综合运用热网络法和有限体积法求解电机温度场，能够更好地掌握电机内传热和换热特性，根据设计周期合理选取电机温度场的求解方法，为电机的热设计提供有效的理论指导和参考价值。

本文以一台25 kW的车用永磁同步电机为研究对象，建立电机的热网络模型，等效计算热网络模型中的热阻，进而通过求解得到电机内各节点的温度；同时建立了电机的三维温度场求解域模型，基于流固耦合基本理论，利用Fluent仿真软件计算电机内各部分的温升，并比较了电机内关键零部件在利用不同方法求解时的温度分布；通过实验平台，验证利用热网络法和有限体积法计算电机温度场的准确性。

1 热网络法求解电机的温度场

1.1 电机的基本参数

电机在设计过程中，基本参数如下：额定功率25 kW，额定转速3 000 r/min，定子内径122 mm，定子槽数48槽，转子外径120.6 mm，转子级数8级，线径0.9 mm，线圈形式采用单层链式。

1.2 电机内热源的计算

在电能驱动电机工作过程中，产生的能量损耗并大部分转化为热量，促使电机温度升高。电机内的发热损耗主要包括定、转子铁心损耗、绕组损耗、永磁体涡流损耗等，通过Ansoft Maxwell电磁仿真计算软件可以精确计算各部分的损耗。在计算电机内损耗过程中，因机械损耗主要产生在轴承处，本文不考虑机械损耗对电机温度场的影响。

1.3 电机散热过程中换热系数和传热系数的计算

在利用热网络法和有限体积法计算电机温度场时，需要考虑到电机内各零部件的端面换热及内部传热。电机内换热系数和传热系数的计算直接影响电机温度场计算的准确性。因此，本文针对电机内各部分，对其换热系数和传热系数一一处理。

(1)端面换热系数处理：电机在工作时，由于转子高速运转，在电机内各零部件必然会与端面空气产生对流换热。本文中，电机内各零部件端面换热系数参考文献[10]进行处理；

(2)定转子气隙传热系数[11]处理：电机工作时，定、转子之间相对运动，电机温度场求解将难以计算。为了降低求解难度，这里假定转子是静止的，通过改变定、转子间隙气体的传热系数来合理等效定、转子之间的传热；

(3)壳体和定子之间的传热系数的处理：电机壳体和定子之间间隙的处理是影响电机散热的重要因素，这里一般根据经验公式将其等效成一层薄空气层进行处理。

1.4 电机热网络模型的建立及求解

1.4.1 电机热网络模型的建立

为了能够利用电机的热网络模型有效、方便地计算电机内各节点的温度，需假定以下条件：

(1)电机散热过程中，热量主要由冷却水带走，不考虑电机机壳的散热；

(2)认为电机内端部空气为等温体；

(3)不考虑换热系数和传热系数随温度的变化；

(4)忽略辐射换热对电机温度场的影响。

根据车用永磁同步电机的基本结构，选取电机的1/4截面，按照电机内各部分相应位置，建立了电机的热网络模型，如图1所示。图中，T1为冷却液温度节点；T2为电机壳体温度节点；T3为定子轭部温度节点；T4为定子齿部温度节点；T5为转子温度节点；T6为电机主轴温度节点；T7为永磁体温度节点；T8为绕组中部温度节点；T9为绕组端部温度节点；T10为转子压板温度节点；T11为端部空气温度节点；T12为电机端盖温度节点。

图1 电机热网络模型

1.4.2 电机热网络模型的求解

根据图2中电机的热网络模型，计算相邻网络节点之间的热阻。根据电机的基本结构，在散热过程中传热分为平壁传热和圆筒壁传热，相应的热阻按如下公式计算：

(1)

(2)

式中:Rp为平壁传热热阻；Rc为圆筒壁传热热阻；δ平壁传热厚度；λ为物体的传热系数；A1为平壁传热面积；r1,r2为圆筒的外径和内径；l为圆筒壁长度。

电机散热过程中，对流换热热阻按下式计算：

(3)

式中:Rh为对流换热热阻；h为对流换热系数；A2为对流换热面积。

计算好电机各部分的热阻后，建立热网络模型对应的电机稳态热平衡方程组,如下式：

(4)

根据电机的热平衡方程组，输入相应的参数后，利用MATLAB软件计算各节点温度，计算结果如表1所示。

表1 热网络模型求解电机温度场结果

2 有限体积法求解电机温度场

2.1 求解域模型的建立

本文中，因电机水道沿轴向均匀分布、水道结构简单，且电机内结构沿径向对称，故取电机的1/8模型为研究对象进行简化处理，简化后的求解域模型如图2所示。

图2 电机求解域模型

针对车用永磁同步电机的温度场计算，根据传热学基本理论，在笛卡尔坐标系内，稳态条件下电机求解域模型满足的通用导热微分方程和边界条件[12]可表示:

(5)

式中:λx,λy,λz为电机内各介质x,y,z方向的导热系数;T为物体的温度；qv为热源密度；S1,S2为物体边界；Tf为流体温度；α为流体与物体壁面间的表面对流换热系数。

本文研究的电机采用强制水冷冷却方式进行散热，当冷却液为不可压缩流体且流动稳定时，需满足相应的三维控制方程如下:

(6)

式中:u,v,w为速度分量；ρ为流体密度；φ为通用变量；K为扩展系数；S为源项。

2.2 模型等效

电机内部结构在简化过程中，绕组和绝缘层处因材料复杂、分布不均、体积较小，在计算过程中不能直接处理，往往需要合理等效。本文将绕组和绝缘层等效层两层导热载体材料，按照质量不变的原则计算两层载体材料的密度、比热容和传热系数。

在仿真计算过程中，电机壳体与定子间隙、定子与转子间隙、电机内端面散热系数均参考热网络法处理方法进行处理。

2.3 有限体积法求解电机温度场

利用所建立的电机温度场求解域模型，通过Fluent仿真软件，设置相应的边界条件，对求解域模型进行计算，得到电机的温度场如图3所示。从电机温度场仿真结果可知，绕组、转子和永磁体平均温升较高，定子平均温升相对较低。电机内最高温度在绕组端部处，温度为94.3℃。电机整体温升较低，温升为34.3℃。

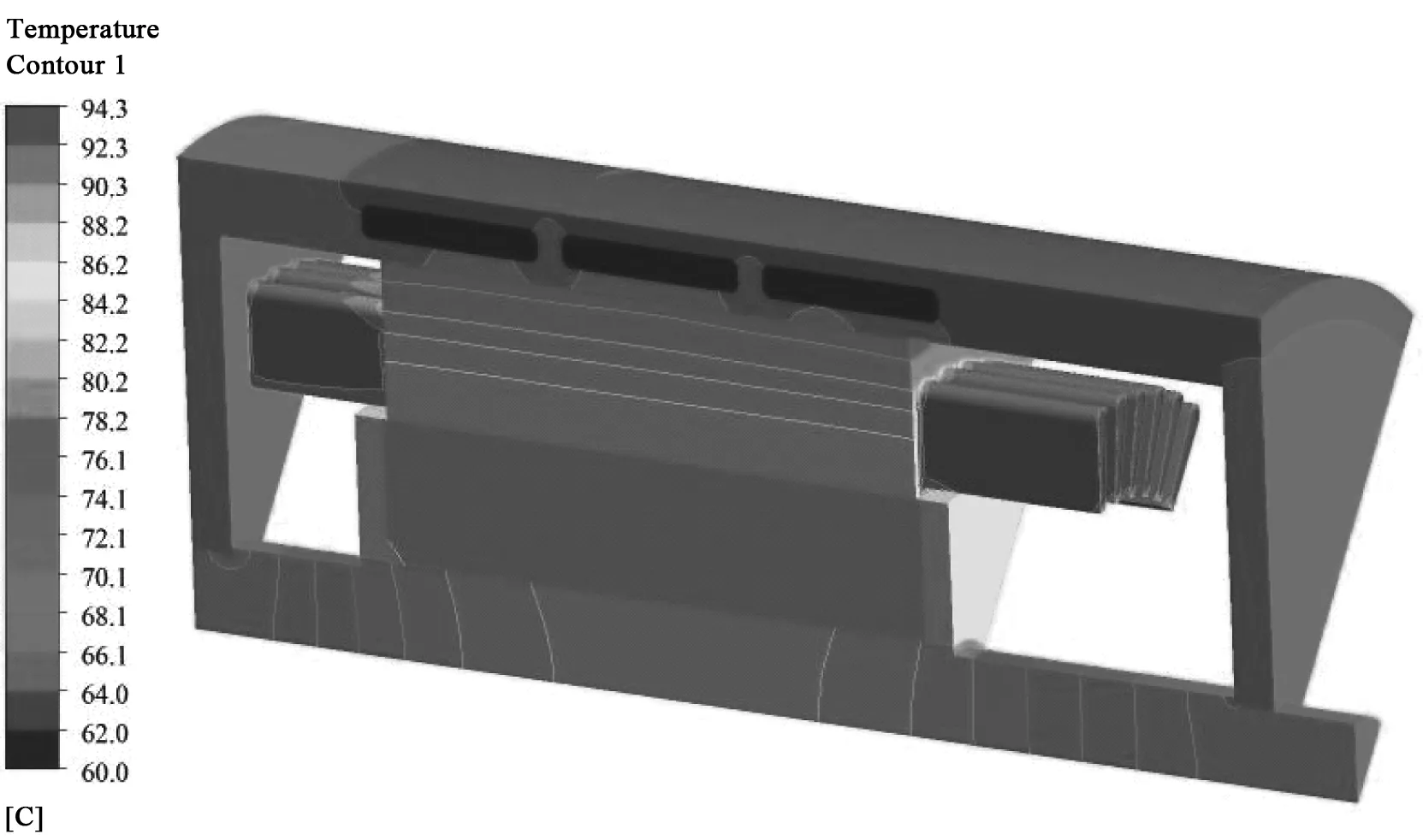
图3 电机全域温度场分布

图4得到了电机求解域模型中截面1和截面2的温度场，截面1相邻于定子端部，截面2位于定子中部。图中，截面1绕组处温度高于截面2绕组处温度，两截面中转子和永磁体温差较小，同时两截面均显示了电机内径向温度梯度的变化。

图4 电机截面1(左)和电机截面2(右)温度场

在利用有限体积法对电机温度场进行求解计算时，可以得到电机内各部分的温度分布。文中，对电机内各零部件进行单独处理，得到的温度分布如表2所示。

表2 电机仿真计算温度场结果

2.4 热网络法与有限体积法求解电机温度场的比较

本文利用热网络法计算出电机内各节点温度，利用有限体积法计算出电机内各部分的温度分布，得到电机内温度较高处主要集中在定子、转子、永磁体和绕组上。通过比较分析，得出利用热网络法和有限体积法计算绕组和永磁体温度分布，如图5所示。图5中横轴0处为定子轴向中心，沿截面1方向为正，得到热网络求解的绕组温度值高于仿真计算求解的绕组温度值，最高温差在-67mm处，温差为5.1℃，最低温差在53.6mm处，温差为3.2℃；利用热网络法求解的永磁体温度值高于仿真计算求解的永磁体温度值，最高温差在±67mm处，温差为2.5℃，最低温差在0，±13.4mm处，温差为0.8℃。

图5 绕组和永磁体温度分布比较

图6显示了定子轭部和定子齿部在热网络法求解和仿真计算求解下的温度分布。图中，以图2中截面1的轴中心为原点，温度沿径向分布，得到热网络法求解的定子轭部和定子齿部温度值均介于仿真值之间。定子轭部的热网络法求解值与仿真最高温度偏差为1℃，与仿真最低温度偏差为1.9℃；定子齿部的热网络法求解值与仿真最高温度偏差为0.3℃，与仿真最低温度偏差为5.9℃。文中，转子温度沿轴向分布类似于永磁体，但分布较为不规则，这里不作赘述。

图5和图6对比分析了利用热网络法和有限体积法计算的电机温度场。热网络法是根据热网络模型中节点数量求解节点温度，节点数量越多，节点温度求解越准确；有限体积法则对计算区域进行网格剖分，并通过网格周围控制体积分进行求解。两种方法对电机温度场的求解有一定偏差，但在合理范围内。

3 实验验证

实验过程中，因为电机内绕组温升较高，且绕组端部温升方便测出，这里将温度传感器埋设在绕组端部，在实验过程中对其温度进行监测。实验平台如图7所示。

图7 实验平台

实验过程中，连接、调试和检查好相关设备后，设置总时间80min，并等分段时间取点，即可得到各时间节点对应的实验电机绕组端部温度值。图8得到了利用热网络法、有限体积法和实验值得到的电机绕组端部温度变化曲线。图中，实验电机工作到64min时温升到达达到稳定，绕组温升达到温度为 93.2℃，仿真计算温度为94.3℃，误差为1.18%；热网络法计算温度为97.9℃，误差为5.04%。

图8 电机绕组温度计算值与实验值的比较

通过比较分析，得出了利用热网络法和有限体积法求解电机温度场的准确性，并且利用有限体积法求解时误差较小，求解更精确。

4 结 语

本文以一台25kW的车用永磁同步电机为研究对象，通过热网络法和有限体积法计算得出电机的温度场，并作对比分析；同时，通过实验验证两种方法在求解电机温度分布的准确性，得出以下结论：

(1)利用热网络法求解电机节点温度时，得到了电机内各部分的温度值，且绕组端部温度最高为97.9℃；

(2)通过有限体积法求解电机温度场时，得到了电机内各部分的温度分布，绕组端部温度最高为94.3℃；

(3)通过比较利用热网络法和有限体积法求解电机温度场时，电机内定子、绕组和永磁体的温度分布，得到了两种方法在求解电机温度场结果的差异性；

(4)通过绕组端部的温升实验验证了利用热网络法和有限体积法求解电机温度场的准确性。

[1] 宋永华.阳岳希.胡泽春. 电动汽车电池的现状及发展趋势[J].电网技术,2011,35(4):1-6.

[2] 黎永键,赵祚喜,高俊文. 混合动力汽车电驱动系统设计与仿真研究[J].农业装备与车辆工程,2012,50(8):4-9.

[3] 彭海涛, 何志伟, 余海阔. 电动汽车用永磁同步电机的发展分析[J].微电机,2010.43(6):78-81.

[4]POPESCUM,DORRELDG,ALBERTIL.Thermalanalysisofduplexthree-phaseinductionmotorunderfaultoperatingconditions[J].IEEETransactionsonIndustryApplications, 2013,49(4):1523-1530.

[5] 宋受俊,张蔓,吴晏辰.基于温度场计算的开关磁阻电机冷却系统设计[J].电机与控制应用,2013,40(9):6-11.

[6] 何磊,王心坚,宋国辉.基于热阻网络法的电机瞬态温度场分析[J].佳木斯大学学报:自然科学版,2014,32(2):187-190.

[7] 程树康,李翠萍,柴凤.不同冷却结构的微型电动车用感应电机三维稳态温度场分析[J].中国电机工程学报,2012,32(30):82-90.

[8] 丁树业,葛云中,孙兆琼,等. 高海拔用风力发电机流体场与温度场的计算分析[J].中国电机工程学报,2012,32(24):74-79.

[9] 丁树业.郭保成.冯海军,等. 变频控制下永磁同步电机温度场分析[J].中国电机工程学报,2014,34(9):1368-1375.

[10] 邰永,刘赵淼. 感应电机全域三维瞬态温度场分析[J].中国电机工程学报,2010,30(30):114-120.

[11] 胡田,唐任远,李岩,等. 永磁风力发电机三维温度场计算及分析[J].电工技术学报,2013,28(3):122-126.

[12] 丁树业,葛云中,徐殿国,等. 1.5MW双馈风力发电机内流体场分析[J].中国电机工程学报,2012,32(21):93-98.

Temperature Field Calculation of Permanent Magnet Synchronous Motor for Pure Electric Vehicles

LIDong-he

(Liaoning Province College of Communications,Shenyang 110122，China)

A rated power of 25 kW PMSM in pure electric vehicles was taken as the research object, lumped parameter method was used to establish a thermal network model of the motor, and the junction temperatures of each parts of the motor were calculated by establishing its thermal equilibrium equations. Meanwhile, the solving domain model of the motor was established by the finite volume method. Fluent software was used to calculate the temperature field of the motor, and the results were compared with the thermal network solution. The calculation results and experimental results were analyzed by means of the experimental platform to verify the use of the thermal network method and finite volume method for solving the accuracy of the motor temperature field.

PMSM； temperature field； thermal network； finite volume method

2015-06-24

TM341；TM351

A

1004-7018(2016)01-0012-05

李东和(1967-)，男，硕士，副教授，研究方向为机械设计与制造。