永磁同步电动机的双闭环分数阶控制研究

文家燕，高 远，刘传国，范健文

(广西科技大学,柳州 545006)



永磁同步电动机的双闭环分数阶控制研究

文家燕，高 远，刘传国，范健文

(广西科技大学,柳州 545006)

为提高永磁同步电动机的转速控制性能和鲁棒性，提出一种双闭环分数阶控制策略，其中电流环和速度环分别采用分数阶积分-微分控制和分数阶比例-积分控制。通过建立永磁同步电动机双闭环分数阶控制系统的数学模型，结合控制系统频域设计理论和功率因数优化方法，设计出速度环和电流环的分数阶控制器，并分析控制系统的稳定性和鲁棒性。控制仿真结果表明，相比传统的整数阶控制情形，即使在不同转速、负载突变的情况下，该双闭环分数阶控制方法不仅能使电机获得更优的转速控制动态性能和鲁棒性，且有效降低定子电流，进一步提高了系统的运行效率。

永磁同步电动机；双闭环控制；分数阶；功率因数；鲁棒性

0 引 言

永磁同步电动机(以下简称PMSM)调速系统在工业生产、数控机床、航空航天和新能源纯电动汽车等领域有着广泛的应用前景。PMSM是强耦合的非线性系统，实际工作环境存在负载扰动、系统参数时变等不确定性因素。控制策略是实现获得高性能PMSM调速系统的重要保证。目前，基于矢量控制技术的PMSM双闭环控制系统，其电流环和转速环大都采用常规的比例-积分-微分(PID)或比例-积分(PI)控制，此类线性控制器虽然可依据精确的PMSM数学模型进行设计，控制方法简单实用，但系统的响应速度和抗负载波动能力较差[1-2]。为改善PMSM的转速输出性能和鲁棒性，人们又提出了自适应控制、滑模控制、模糊控制等矢量控制方法[3-4]。

近几年，人们发现分数阶控制能明显提高被控系统的控制性能和鲁棒性[5]，因此有学者开始关注PMSM的分数阶控制研究[6-10]。文献[6]和文献[7]分别将速度环的整数阶PI和PID控制器扩展成分数阶形式，并给出分数阶控制器参数的整定方法，研究表明，分数阶PI和PID控制器的控制效果均明显优于其整数阶控制情形。文献[8]采用混合差分人工蜂群算法对分数阶PI控制器的控制参数进行自适应调整，进一步提高了PMSM 调速系统的自适应性、动静态性能以及抗外界干扰能力。文献[9]定义分数阶的滑模函数，并设计速度环分数阶滑模控制器，并给出控制参数的设计方法。然而，从现有资料看，已有报道均根据d轴定子电流id=0的PMSM线性化解耦模型，对系统的速度环设计分数阶控制器，电流环仍采用传统的整数阶PI控制形式。

鉴于PMSM的电流、转速双闭环调速控制系统，其转速环(外环)的性能发挥依赖于电流环(内环)的性能优化；电流环是PMSM调速伺服系统中的一个重要环节，它对提高控制响应速度，以及改善控制系统整体性能方面有着重要作用[11]；分数阶控制能进一步增强系统的控制性能和鲁棒性。因此，本文进一步研究PMSM的双闭环分数阶控制方法，并提出一种转速环采用分数阶比例积分(FO-PI)控制、电流环实施分数阶积分微分(FO-ID)控制的控制策略。研究首先建立PMSM双闭环分数阶控制系统的数学模型，然后借助频域设计理论和功率因数优化思想，设计出转速环和电流环的分数阶控制器, 并分析系统的控制稳定性。PMSM双闭环控制系统的控制仿真结果表明：相比传统的双闭环整数阶比例积分(IO-PI)控制，以及转速环FO-PI、电流环IO-PI的控制情形，PMSM的双闭环分数阶控制不仅能使电机获得更优的转速动态性能和抗负载跳变能力，且明显改善电机功率因数，提高系统效率。

1 PMSM双闭环分数阶控制系统

采用id=0的矢量控制技术，并假定电机d-q轴的等效电感Ld=Lq=L,图1是PMSM转速、电流双闭环的分数阶控制系统原理图。相比传统的双闭环矢量控制系统而言，图1中的电流环和速度环均采用分数阶控制器。图2是双闭环分数阶控制系统的动态结构示意图。图2中，R是定子绕组电阻；φf为永磁体产生的磁势；TL是负载转矩；p为定子磁极对数；J是转子转动惯量；Kc=3pφf/2为转矩系数；ω和ωr分别是电机转子实际转速和期望转速；K1/(τ1s+1)代表具有增益K1、滤波时间常数τ1的 电流反馈滤波环节；K2/(τ2s+1)则表示存在增益K2和滞后时间常数τ2的三相PWM逆变器。

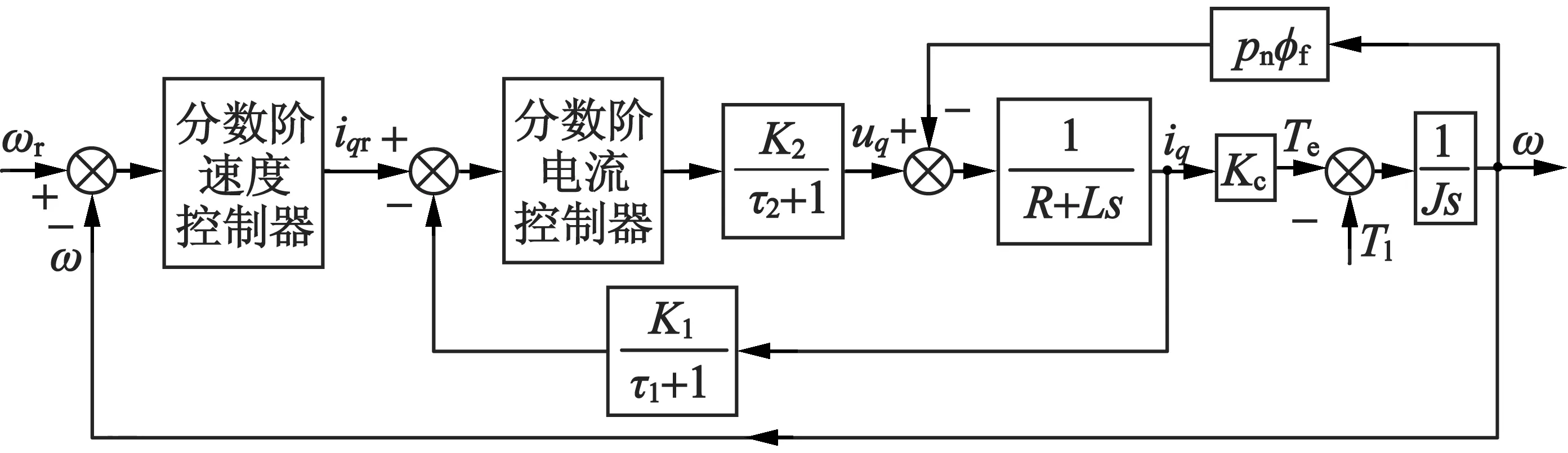
图2 PMSM双闭环分数阶控制系统动态结构示意图

由于τ1和τ2的数值很小，电流反馈滤波环节和PWM逆变器均可视为小惯性环节，结合小惯性环节的处理方法，可得出电流环控制对象的开环传递函数[12]：

(1)

式中:KR=1/R，Ti=τ1+τ2，Tm=L/R是电机电枢回路的电磁时间常数。

1.1 PMSM的双闭环分数阶控制器

本文所采用的电流环、转速环分数阶控制器分别：

(2)

和

(3)

式中：α,λ∈(0,1)是分数阶积分阶次参数;Ki和Kv是控制器的放大倍数;τi和τv为控制器的积分时间系数。式(2)和式(3)分别具有FO-ID和FO-PI结构，显然，当α=λ=1时，双闭环控制器则变为传统的IO-PI控制形式。

1.2 双闭环分数阶控制系统的数学模型

结合式(1)和式(2)可推导出电流环闭环传递函数：

(4)

取τi=Tm，使电流环控制器的零点对消被控对象的时间常数极点，定义T=τi/(K1K2KRKi)，则式(4)变成：

(5)

鉴于速度环的截止频率较低，且Ti≪τi≪1s，所以式(5)可经降阶处理：

(6)

因此，转速环被控对象的等效模型：

(7)

其中K=Kc/J。因此，式(7)的频率特性：

(8)

(9)

结合式(3)和式(7)可得出速度环开环传递函数及其频率特性：

(10)

(11)

(12)

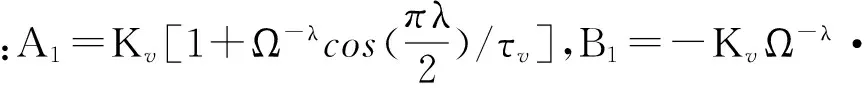
2 双闭环分数阶控制器设计

根据控制系统频域设计理论可知，当设定系统的截止频率Ωc和相位裕度φm，在系统稳定性和鲁棒性要求条件下，开环传递函数G(s)的相位和幅值应满足如下设计准则[13]：

i) 相位裕度准则：

(13)

ii) 系统增益变化的鲁棒性准则：

(14)

iii) 幅值准则：

(15)

对于上述的电流、转速双闭环分数阶控制器，除τi=Tm外，共有5个待设计的控制器参数，故难以利用以上3个频域设计准则对参数进行直接求解。因此，本文采取如下步骤的分步混合方法对电流环和速度环控制器进行设计。

步骤1：设计电流环IO-PI控制器

结合式(5)，当α=1时，要求超调量≤5%，取阻尼比为0.707，T=2Ti，并结合τi=Tm=L/R，可求出：

(16)

步骤2：设计转速环FO-PI控制器

在设计出电流环IO-PI控制器基础上, 选取截止频率Ωc和相位裕度φm，根据准则i和式(12)，可得：

(17)

根据准则ii和式(12)可得：

(18)

根据准则iii和式(11)可得：

(19)

根据式(17)和式(18)，可通过τv～λ关系图取交点的方法求解出τv与λ，进而利用式(19)求出Kv。对于λ=1的整数阶控制情形，为兼顾控制系统的相位裕度和鲁棒性要求，τv取式(17)和式(18)两个直接解的平均值。

步骤3：设计电流环FO-ID控制器的分数阶次α

对电流环IO-PI控制器按式(2)分数阶化，在τi和Ki不变的情况下，考虑期望转速运行工况，根据功率因数最大准则对电流环控制器的分数阶次α在(0,1]范围内进行优化搜索。其中，功率因数[14]：

(20)

式中：θ表示功率因数角。

PMSM主要参数如表1所示。当取表1所列电机系统参数，可按步骤1可求出τi=0.004，Ki=4.789，故电流环IO-PI控制器：

(21)

表1 PMSM系统主要参数

选取截止频率Ωc=1 000 rad/s，相位裕度φm=π/3，根据步骤2可获得如图3所示的τv与λ关系

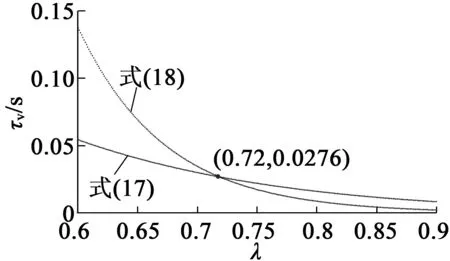
图3 τv与λ的关系曲线

曲线图。根据曲线交点可知λ=0.72，τv=0.027 6，并结合式(19)求出Kv=0.461 7。因此，速度环FO-PI控制器：

(22)

当λ=1时，可直接求出：

(23)

选择电机期望转速3 500r/min，根据步骤3，在控制器式(21)和式(22)的基础上，按照电机功率因数最大原则，对电流环控制器的分数阶次α进行优化搜索。图4是功率因数cosθ随α的变化曲线。

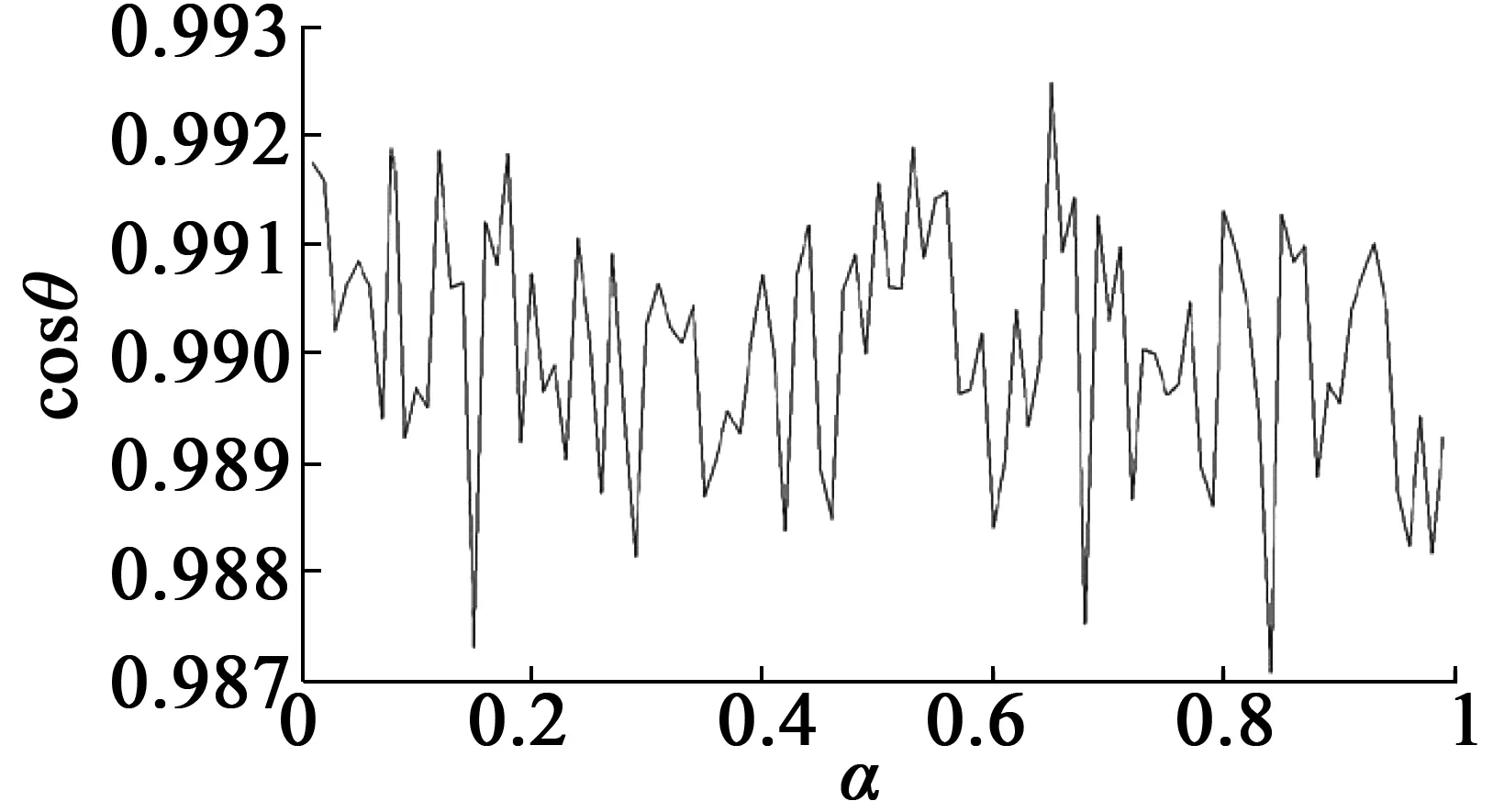
图4 功率因数随α的变化曲线

由图4看出，当α=0.65时，功率因数有最大峰值。因此，电流环FO-ID控制器：

(24)

图5是速度环开环传递函数的Bode图。由图5可见，传统的双闭环IO-PI控制(λ=1,α=1)，以及转速环FO-PI、电流环IO-PI控制情形(λ=0.72,α=1)下的速度环开环传递函数，其幅值曲线几乎完全重合，相位曲线反映出相位裕度与设计要求存在一定偏差，相比前两者控制情形，PMSM双闭环分数阶控制 (λ=0.72,α=0.65)的Ωc和φm均符合设计要求，且相位曲线在Ωc=1 000 rad/s处的平坦范围较宽，这也表明双闭环分数阶控制系统具有更强的控制鲁棒性。

图5 速度环开环Bode图

3 控制仿真结果及分析

结合图1，在MATLAB/Simulink环境下建立PMSM的双闭环分数阶控制系统仿真模型，其中分数阶微积分的数值计算利用Oustaloup滤波方法实现[16]。为验证本文所提出双闭环分数阶控制方法的有效性和先进性，仿真中也给出了双闭环IO-PI控制(λ=1,α=1)，以及转速环FO-PI控制、电流环IO-PI控制(λ=0.72,α=1) 的结果。

取期望转速为3 500 r/min。图6示出了PMSM的转速变化曲线。从图6看出，三种不同控制方法均能实现PMSM对期望转速的稳定跟踪控制，且无超调，但双闭环分数阶控制却能使得PMSM获得更优的转速动态性能。

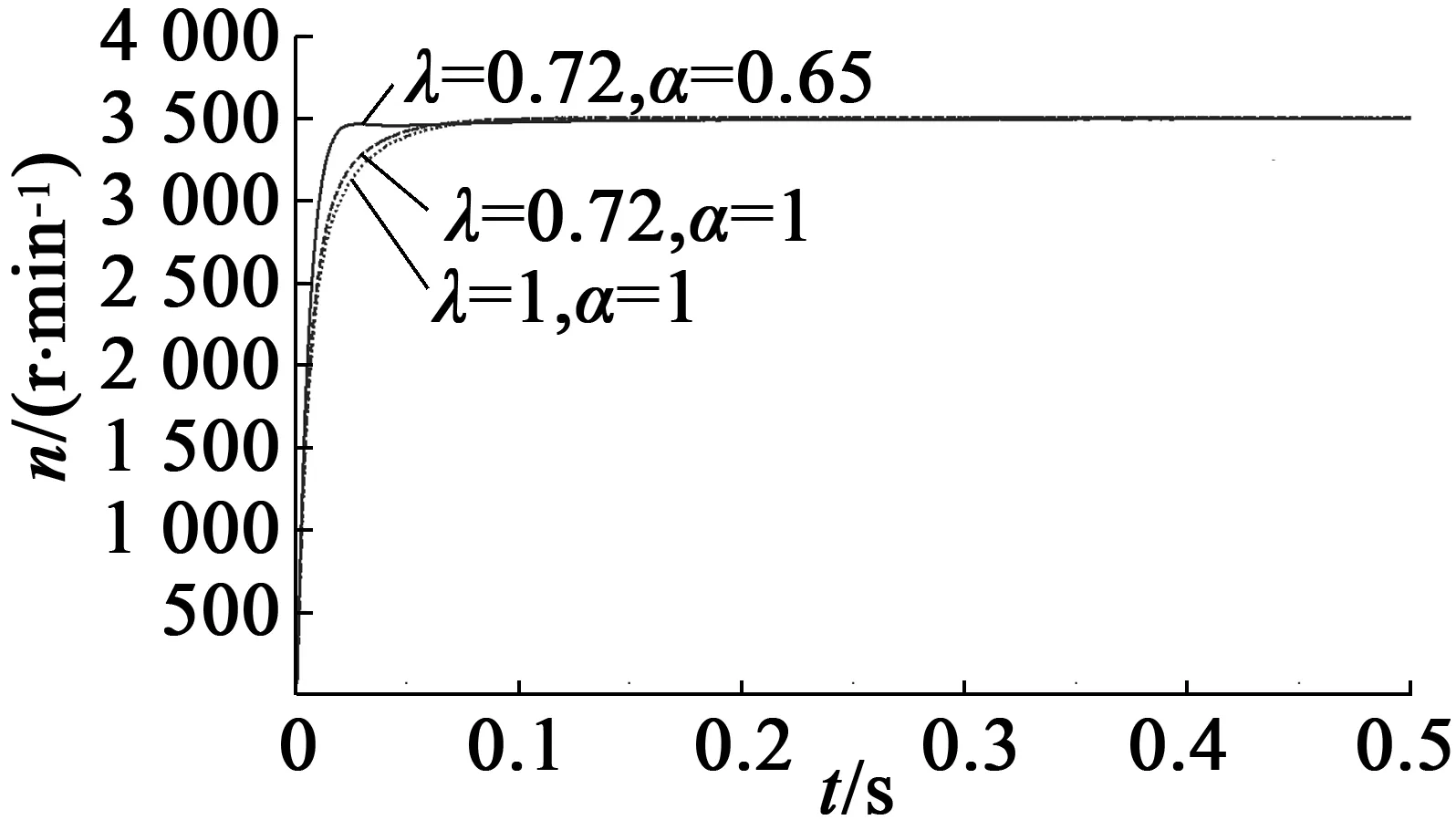
图6 电机转速

图7和8分别是q轴定子电流和电机功率因数的变化曲线图。由图7和图8可见，在双闭环分数阶控制器作用下，q轴定子电流幅值最小且稳态精度较好，功率因数获得明显提高。这表明双闭环控制系统中的电流环FO-ID控制器不仅能进一步改善电流环的电流跟踪控制能力，且q轴定子电流较小，电机铜耗降低，从而提高了系统效率。

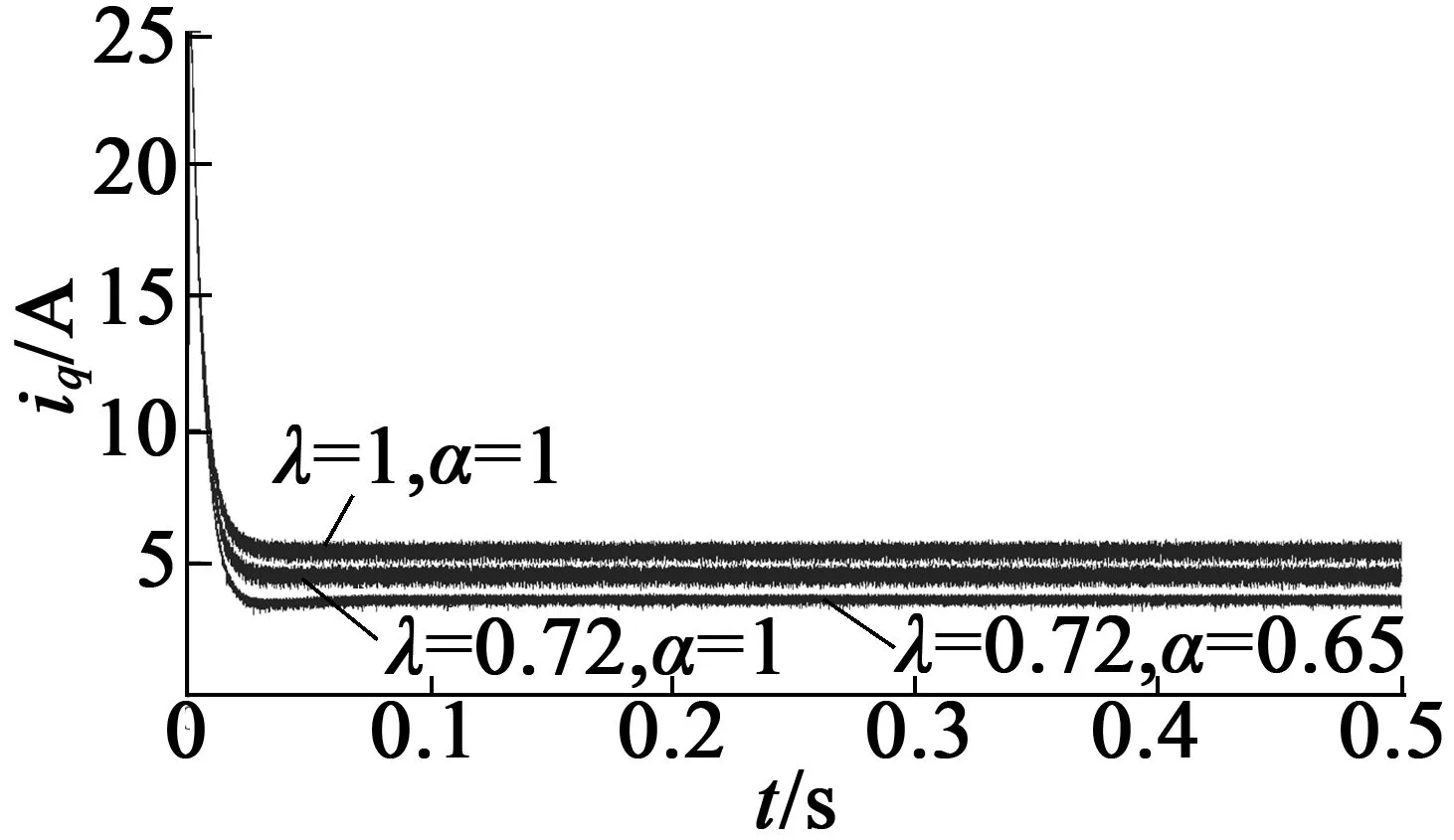
图7 q轴定子电流

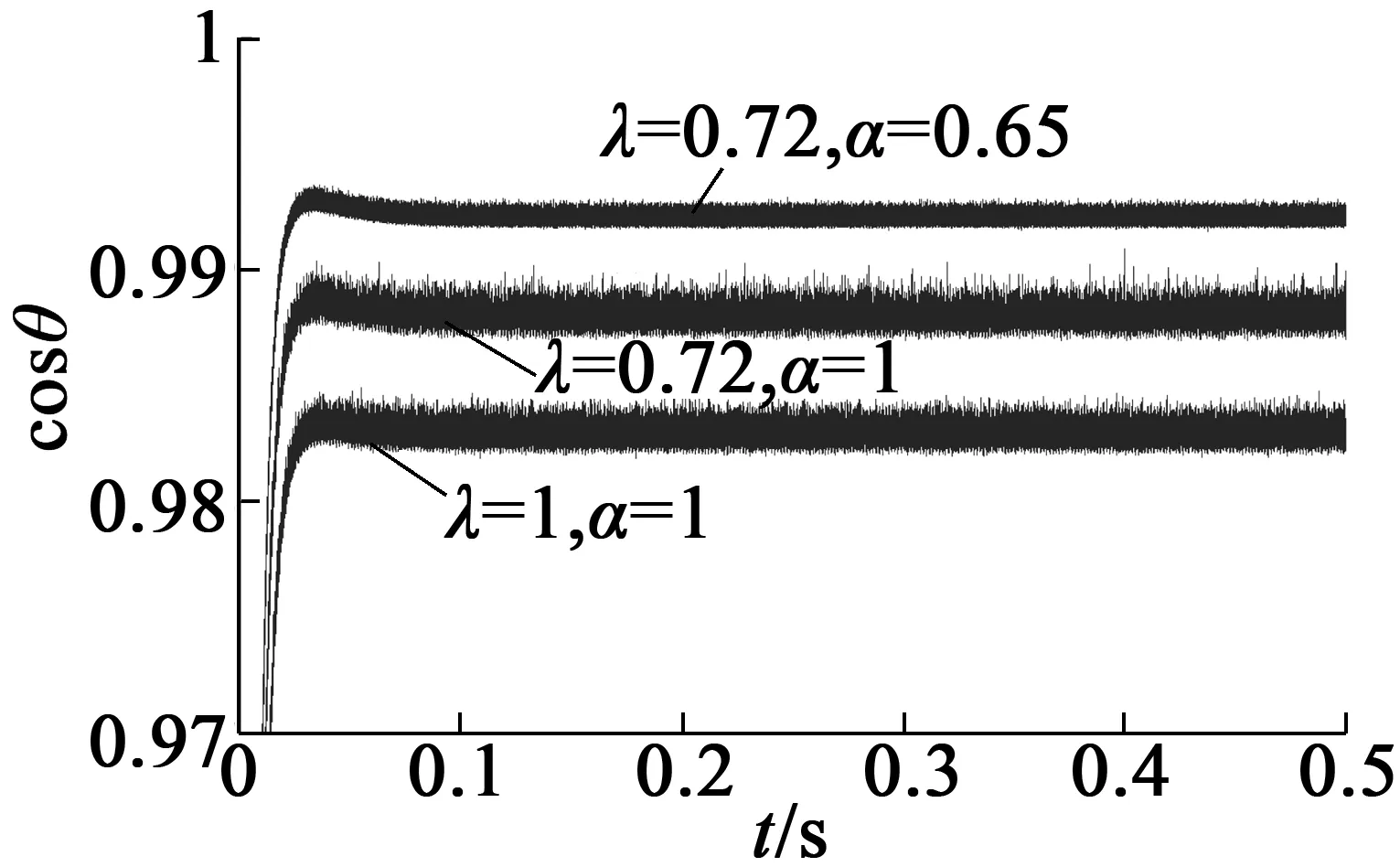
图8 功率因数 (局部图)

当负载转矩在t=0.1 s由2 N·m跳变为4 N·m，图9和图10分别给出了负载跳变时电机转速和功率因数的变化曲线。由图9明显看出，在跳变时刻，双闭环分数阶控制，PMSM转速波动最小。图10反映出当负载转矩增加时，虽然三种控制方法的功率因数均有所降低，但双闭环分数阶控制下的PMSM，功率因数减少幅度最小。这表明，双闭环分数阶控制策略能使PMSM具有良好的抗负载变化能力。

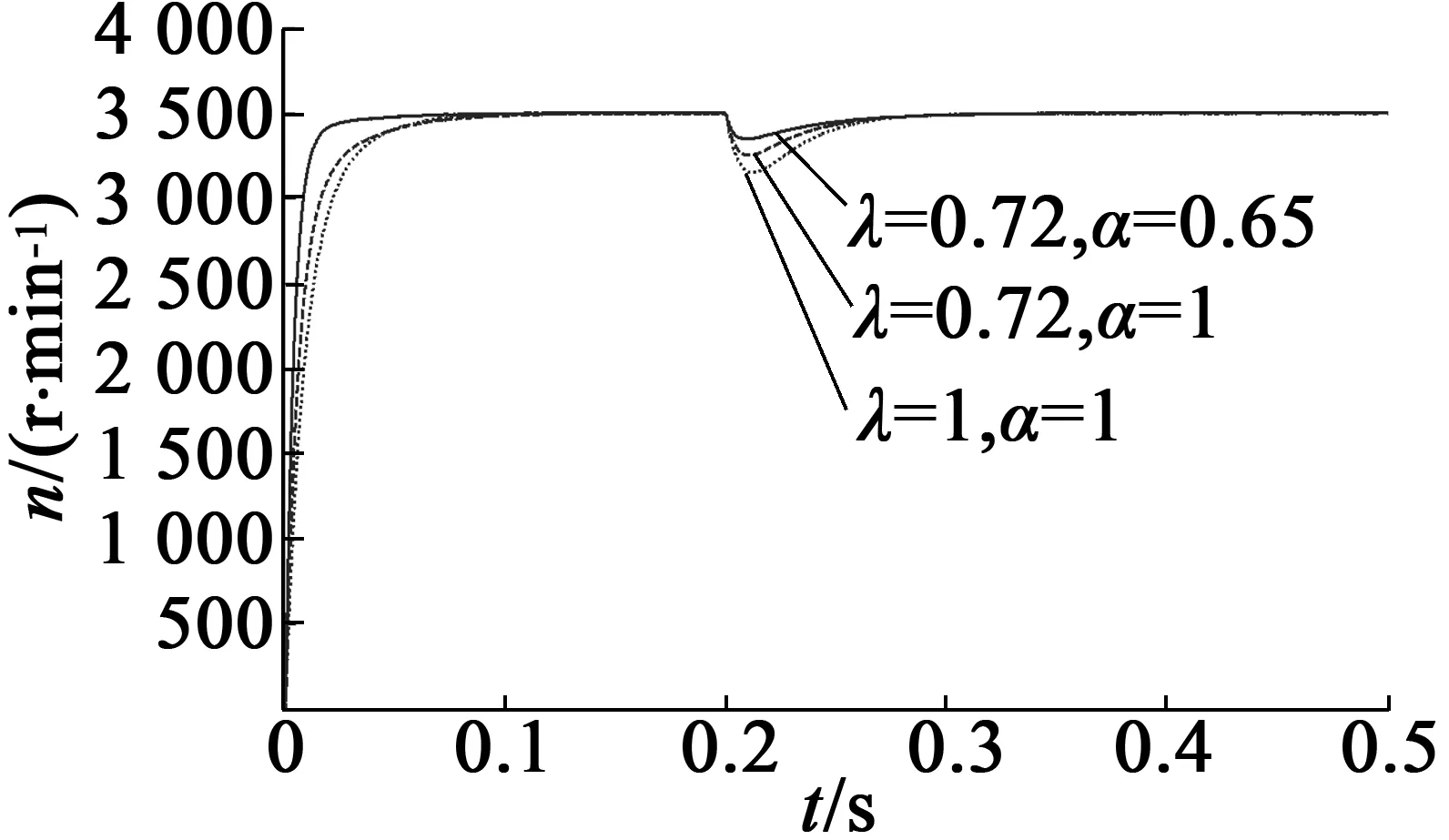
图9 电机转速

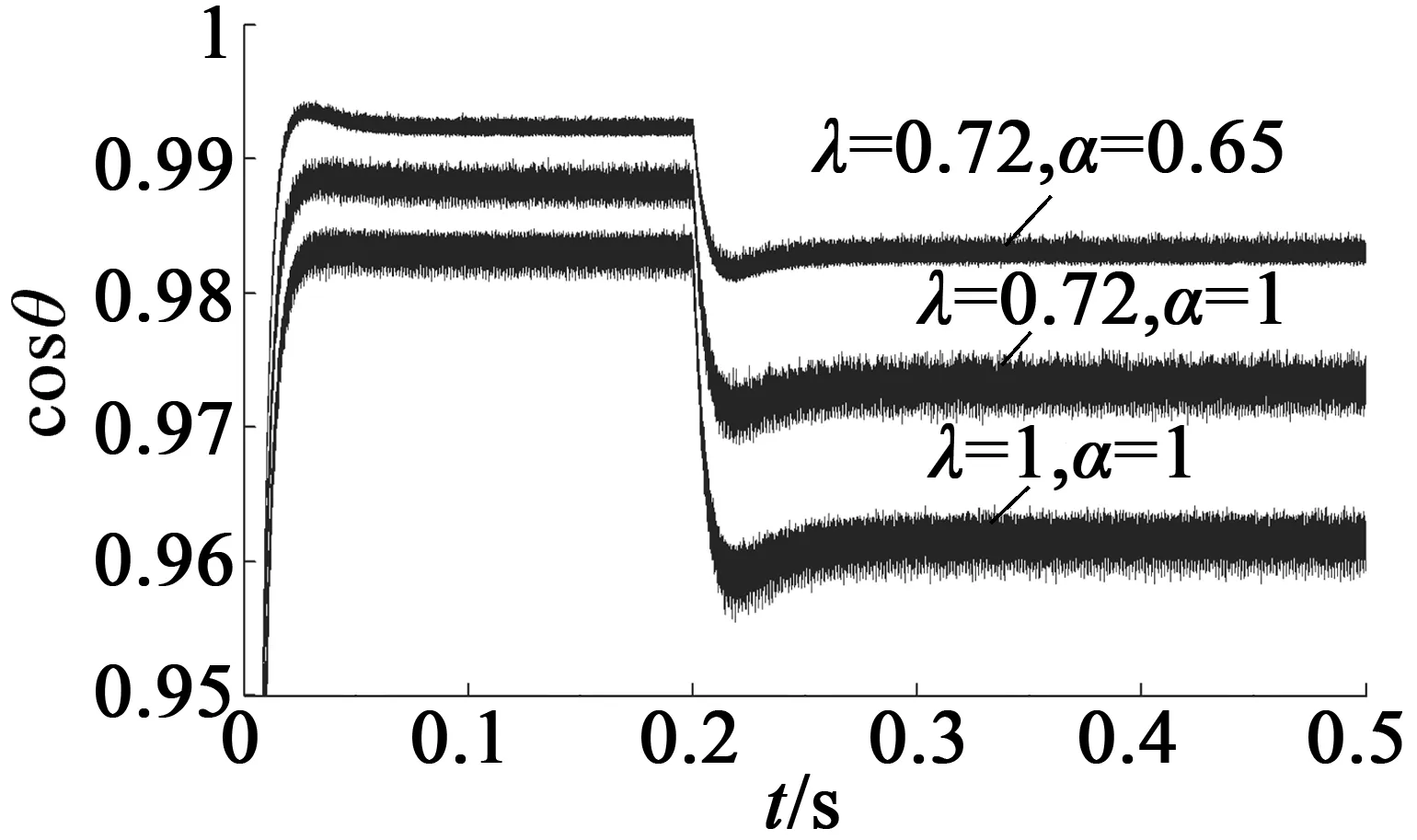
图10 功率因数

考虑期望转速在0.2 s处由2 000 r/min加速至4000r/min，然后在0.4s处由4000r/min减速到3 000 r/min的变速控制情况。图11和图12分别是电机转速和功率因数的变化曲线图。由图11看出，双闭环分数阶控制方法具有较快的起控速度，且在控制电机高速运行条件下，超调现象也最小；同时，图12也反映出不同期望转速条件下，双闭环分数阶控制方法仍具有较大的功率因数。这表明在变速情况下，相比于其他两种控制方法，双闭环分数阶控制仍具有较好的动态控制性能，且使系统保持较好的工作效率。

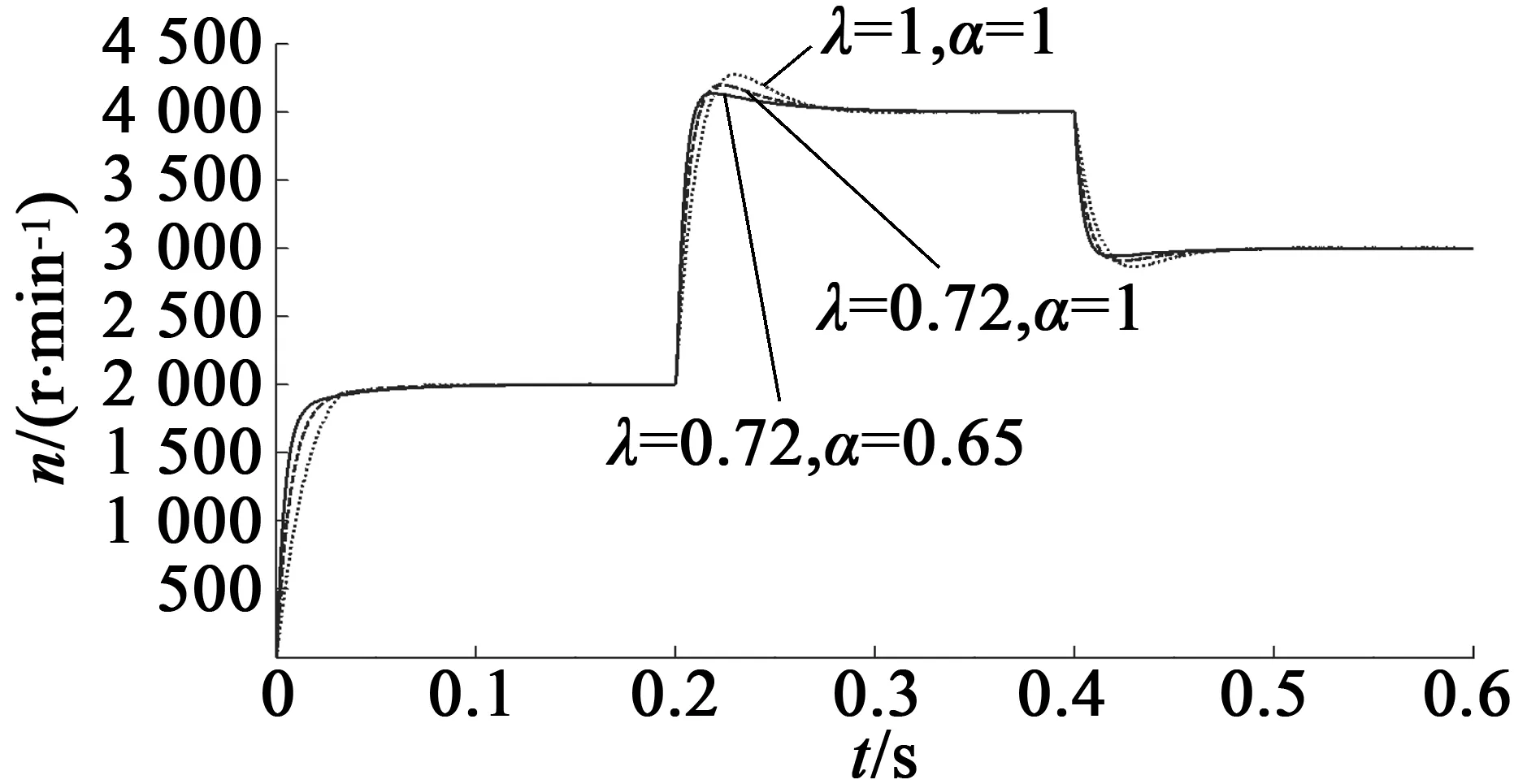
图11 电机转速

图12 功率因数(局部图)

4 结 语

本文在建立PMSM转速环和电流环的双闭环分数阶控制系统数学模型基础上，结合控制系统频域设计理论和功率因数优化思想，给出了电流环FO-ID控制器和转速环FO-PI控制器的设计方法，并分析了电机转速控制系统的稳定性和鲁棒性。仿真结果表明，相比传统的双闭环IO-PI控制，以及转速环FO-PI和电流环IO-PI的控制方案，电流环FO-ID和转速环FO-PI的双闭环分数阶控制能获得了更优的转速控制动态性能，且进一步提高PMSM抗负载突变能力和功率因数。

[1] JAN R M,TSENG C S,LIU RJ.Robust PID control design for permanent magnet synchronous motor:a genetic approach[J].Electric Power Systems Research,2008,78 (7):1161-1169.

[2] 纪厉,徐龙祥.高速永磁同步电动机无传感器控制[J].电机与控制学报,2011,15(9):24-30.

[3] 吴红星,钱海荣,刘莹, 等.永磁直线同步电机控制技术综述[J].微电机,2011,44(7):76-80.

[4] 辛小南,贺莉,王宏州.永磁同步电动机交流伺服系统控制策略综述[J].微特电机,2010,38(2):67-70.

[5] 朱呈祥,邹云.分数阶控制研究综述[J].控制与决策,2009,24(2):161-169.

[6] 王瑞萍,史步海,皮佑国.基于分数阶控制器的PMSM 恒速控制[J].华南理工大学学报,2012,40(3):119-126.

[7] 钟其水,李辉.永磁同步电动机分数阶微积分控制方法研究[J].电子科技大学学报, 2011, 40(2):246-249.

[8] RAJASEKHAR A,ABRAHAM A,PANT M.A hybrid differential artificial bee colony algorithm based tuning of fractional order controller for permanent magnet synchronous motor drive[J].International Journal of Machine Learning and Cybernetics, 2014,5(3):327-337.

[9] ZHANG BT,PI YG,LUO Y.Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor[J].ISA Transactions,2012,51(5):649-656.

[10] 张碧陶,皮佑国.基于模糊分数阶滑模控制的永磁同步电动机控制[J].控制与决策，2012,27(12):1776-1780.

[11] 舒志兵,周玮,李运华,等.交流伺服运动控制系统[M].1版.北京：清华大学出版社,2006.

[12] 陈荣. 永磁同步电动机控制系统[M].北京：中国水利水电出版社,2009.

[13] 胡寿松.自动控制原理[M].北京:科学出版社,2007.71-120.

[14] 刘文良,张国政.永磁同步电动机单位功率因数控制[J].微电机,2012,45(2):63-67.

[15] 龚云飞,富厉新.基于MATLAB的永磁同步电动机矢量控制系统仿真研究[J].微电机,2007,40(2):33-36.

[16] 薛定宇.控制系统计算机辅助设计[M].2版.北京:清华大学出版社,2006.

Control of PMSM via a Double Closed-Loop Fractional-Order Control Strategy

WENJia-yan,GAOYuan,LIUChuan-guo,FanJian-wen

(Guangxi University of Science and Technology,Liuzhou 545006,China)

A double closed-loop fractional-order control strategy was presented for improving the control performances and robustness of permanent magnet synchronous motor (PMSM), in which current loop and speed loop adopted fractional-order integral-differential controller and fractional-order proportional-integral controller, respectively. Firstly, the mathematical model of the controlled PMSM system with double closed-loop fractional-order controller was built. Secondly, from the mathematical model, the fractional-order controllers of speed loop and current loop were designed according to the frequency domain theory and the optimization method of the power factor, and the robustness of fractional-order control system was discussed. The simulation results demonstrate that under the conditions of various speeds and load jump, comparing the integral-order situation, this double closed-loop fractional-order control method can not only obtain better speed dynamic performance and robustness of the PMSM speed servo system, but also further improve the efficiency of PMSM system.

permanent magnet synchronous motor; double closed-loop control; fractional-order; power factor; robustness

2015-08-19

广西自然科学基金项目(2014GXNSFBA118284,2013GXNSFAA019351);广西科技大学青年基金项目(1307116)

TM341；TM351

A

1004-7018(2016)01-0034-05

文家燕(1981-),男，讲师，研究方向为电机控制研究。