宽带定向耦合器的设计与应用

王家波，曹雪松

（南京电子器件研究所，南京 210016）

宽带定向耦合器的设计与应用

王家波，曹雪松

（南京电子器件研究所，南京 210016）

对耦合线定向耦合器进行理论分析，对于对称型，首先求得多节定向耦合器的耦合度通用表达式，然后利用二项式（最平坦）响应前n-1阶导数为零的条件，计算出各节耦合系数。对于非对称型，利用四分之一波长耦合器与四分之一波长阶梯阻抗滤波器等效，通过切比雪夫多项式及理查德变换综合出阶梯阻抗滤波器的归一化阻抗，此即为耦合器的偶模阻抗，然后计算出各节耦合系数。实例计算比较4～20 GHz的两种耦合器：二项式响应耦合器具有最平坦的带内特性；与二项式响应相同节数的切比雪夫响应耦合器具有更大的带宽比。最后用厚度为0.254 mm的Rogers 5880微带板制作了6～18 GHz的两节微带线耦合器，并应用在某组件中。

二项式响应；切比雪夫响应；宽带定向耦合器

1　引言

定向耦合器广泛应用于微波测试仪器仪表和雷达、移动通信、卫星通信等系统之中。常见的耦合器有波导孔耦合定向耦合器和耦合线定向耦合器。波导耦合器为立体结构，不适用于平面电路结构；为了抑制高次模，带宽有一定限制。耦合线定向耦合器大多采用传输纯TEM模的带状线和准TEM模的微带线，带状线耦合方式有宽边耦合、偏置耦合和窄边耦合。为了得到更大的带宽比、更小的耦合系数变化（波纹系数），耦合器采用多节级联方式，每节长度为中心频率的四分之一波长。

本文对耦合线定向耦合器进行理论分析，得到多节定向耦合器的耦合度通用表达式，并使用Matlab、ADS软件设计仿真比较4～20 GHz具有二项式（最平坦）响应和切比雪夫（等波纹）响应的-15 dB微带平行耦合器和带状线窄边耦合耦合器，最后使用ADS和HFSS软件设计仿真并根据实际使用要求制作了6～18 GHz、-25 dB的微带线耦合器。

2　理论分析

2.1单节耦合器

我们用奇偶模分析法分析单节耦合线耦合器。对于纯TEM传输线，奇偶模相速相等，所以

利用奇偶模反射系数(Γ)、传输系数(T)和传输矩阵(A)的关系，可得散射矩阵(S)的表达式为[1]：

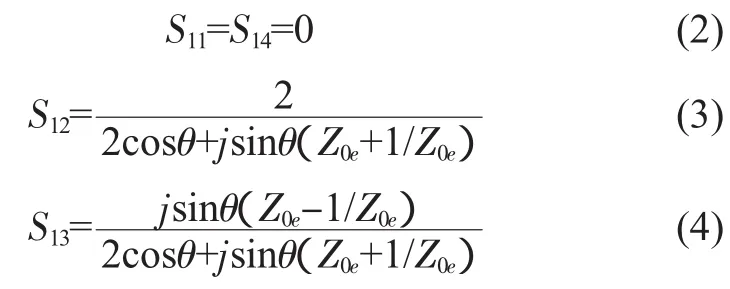
当耦合线长度为中心频率四分之一波长，即θ= π/2时，匹配的、弱耦合的耦合器中心频率处的耦合系数k为：

耦合器耦合系数和传输系数的频率特性为：

对于弱耦合的准TEM传输线，式(1)近似成立，所以上述表达式能适用于准TEM模的微带线和纯TEM模的带状线。单节四分之一波长平行耦合线耦合器的带宽通常约为一个倍频程[1]。

2.2宽带多节耦合器

多节耦合器由两节以上的单节耦合器级联而成，每一节的长度在中心频率都是四分之一波长[1]，所用的节数取决于允许的插入损耗、带宽、耦合度平坦度和实际可用的空间。多节耦合器可分为对称型和非对称型两类。对称型以中心节对称，其第i节与第(n-1+i)节完全相同，节数n为奇数；非对称型耦合器的耦合线间距从头到尾单调递增(或递减)，其节数n既可以是奇数，也可以是偶数。

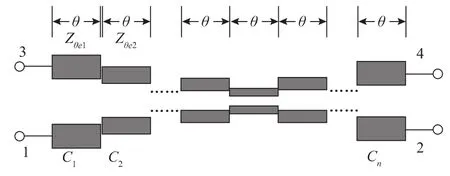
图1　多节耦合线耦合器

2.2.1多节对称耦合器

对于单节弱耦合，耦合系数k=1，式(6)和式(7)可近似为：

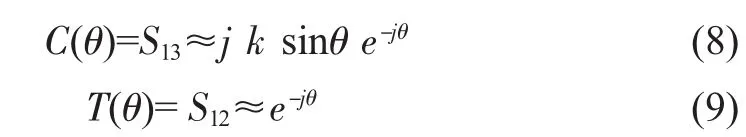
因此，多节耦合器耦合系数可表示为：

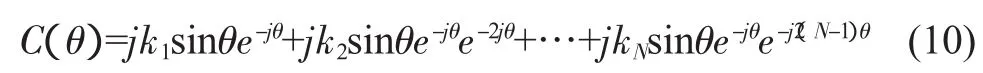
其中kn是第n节电压耦合系数。对于对称结构kn=kN-n+1，上式的模可简化为：

对于最平坦耦合特性（二项式响应），则ki满足：

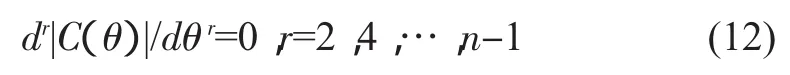
2.2.2多节非对称耦合器

对于多节非对称耦合线耦合器，我们利用单节四分之一波长耦合器与四分之一波长阶梯阻抗滤波器等效，用四分之一波长阶梯阻抗滤波器作为多节定向耦合器的原型，先综合出四分之一波长阶梯阻抗滤波器，再变换成定向耦合器。

单节四分之一波长阶梯阻抗滤波器反射系数和传输系数为[2]：

与式(3)和式(4)比较可知：若四分之一波长阶梯阻抗滤波器归一化阻抗Z1等于定向耦合器的归一化偶模阻抗Z0e，则该滤波器的反射系数等于定向耦合器的耦合系数(S13)；滤波器的传输系数等于定向耦合器的传输系数，两者完全等效。所以可得插入损耗和耦合度关系：

对于多节四分之一波长阶梯阻抗滤波器，可分解成若干个单节四分之一波长阶梯阻抗滤波器相级联。级联传输矩阵为A，矩阵元素都是cosθ的多项式。级联二端口网络的衰减函数可表示为：

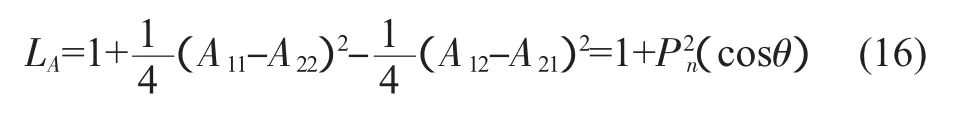
定向耦合器通常要求在频带内具有一定的波纹特性，而切比雪夫多项式正好满足这个要求。n节非对称定向耦合器，衰减函数可表示为[3]：

式中Tn为第一类n阶切比雪夫多项式。

耦合器通带范围为（θ1,π-θ1），利用初始条件结合式(15)可求得：

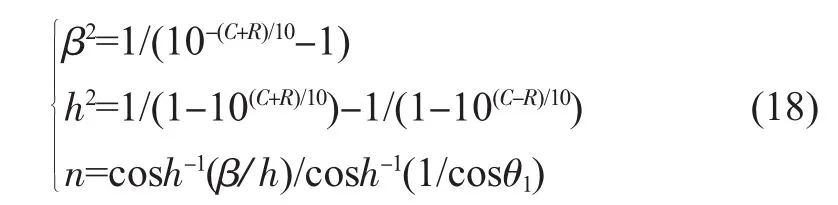
反射系数的模平方可表示为：

分别求反射系数分子分母的根，并利用理查德变换t=tanhjθ=jtanθ综合出各节偶模阻抗[4]，利用式(5)计算出各节耦合系数，得到每节耦合度C。阶梯阻抗滤波器综合过程和各节耦合器偶模阻抗计算公式可见参考文献[4]。

文献中n=4的表达式（88）的b3、c3应为：

文献中n=5的表达式（96）、（97）、（98）应为：

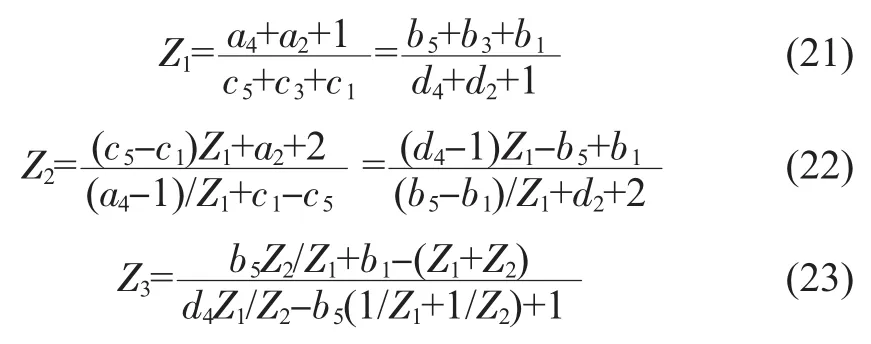
3　仿真设计与比较

对于4～20 GHz频带内，耦合度-15 dB时（若耦合度较小会出现耦合度-40 dB以下的单节，从而限制节数），我们计算比较了2节、3节、4节等波纹响应耦合器的耦合度曲线，以及2节非对称型和3节对称型最平坦响应耦合器的耦合度曲线。对于带状线耦合器和微带线耦合器，它们各节耦合度是一样的，理论初值用matlab编程计算，见表1。

表1-15　dB耦合线定向耦合器各节耦合度初值

在ADS中由耦合度计算出各节微带线耦合器和带状线耦合器的物理参数：长度、间距、线宽。优化各参数后仿真结果如图2和图3。

图2　多节等波纹和最平坦响应微带线耦合器耦合度

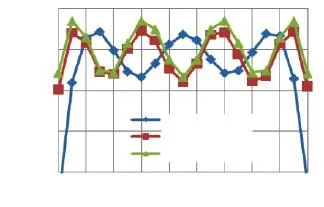
图3　相同波纹系数的3、4节微带线和带状线耦合器耦合度

从图2和图3中我们可以看出：

（1）对于给定带宽比的等波纹响应，节数越多，波纹越小。

（2）节数相同的情况下，等波纹响应带宽比大于最平坦响应。以3节为例，等波纹响应带宽比为5，最平坦响应带宽比约为3。

（3）相同波纹系数下，节数越多，带宽比越大。4节等波纹响应带宽比为7，3节带宽比为5。

（4）相同节数的微带线耦合器和带状线耦合器耦合度仿真结果完全一致，说明对于准TEM模的微带线耦合器理论推导所取的近似可行。带状线耦合器的隔离度和直通损耗优于微带线，这是由两种传输线的结构决定的。

4　工程应用

在某6～18 GHz收发组件中，为了标校输出功率与接收增益，我们需要耦合度约为-25 dB左右的耦合器，平坦度±1 dB以内。微带线定向耦合器易于加工，能与微波平面电路良好可靠互联，性能与带状线一致，因此我们采用微带线结构。

各节耦合度理论初值见表2。

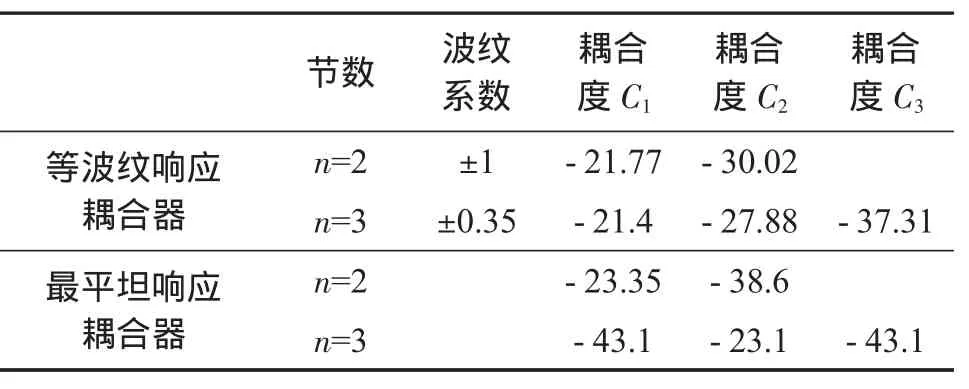
表2-25　dB耦合线定向耦合器各节耦合度初值

在ADS中计算各参数后，优化仿真结果如图4所示。

可见2节等波纹和最平坦都能满足要求。由于组件空间和结构限制，我们以4～20 GHz两节等波纹为初值优化，并将第二节的1/4波长段拆分为两节1/8波长段，分别置于第一节耦合段两边。ADS与HFSS建模仿真结果见图5；厚度0.254 mm、介电常数2.2的Rogers介质板制作的耦合器实物照片见图6；耦合度、直通损耗、驻波测试结果见图7和图8。

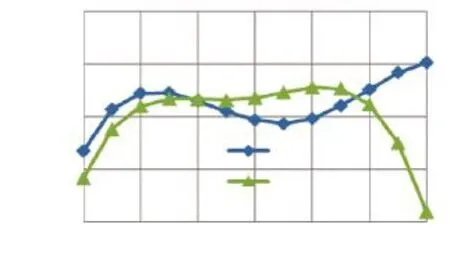
图5　6～18 GHz两节耦合器建模仿真计算

图6　Rogers介质板制作的耦合器照片

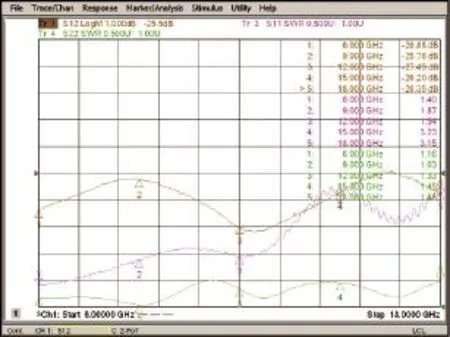
图7　耦合器耦合端测试结果

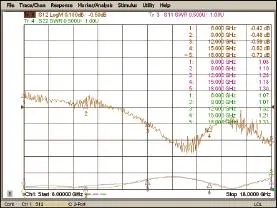
图8　耦合器直通端测试结果

实测结果可以看到直通损耗约为0.65 dB；耦合度约为-26.5 dB，扣除实际损耗并考虑加工误差，与仿真-24.5 dB基本吻合；实际波纹（±1 dB）和频率特性介于ADS与HFSS仿真之间；耦合口驻波高频段较差，这与隔离端口使用的电阻有较大关系；直通端与耦合端相位差95°，与理论值90°符合。

5　结论

本文介绍了二项式（最平坦）响应和切比雪夫（等波纹）响应多节耦合器设计公式的推导，并对带宽、波纹等特性设计仿真进行比较：给定带宽内，节数越多波纹系数越小；相同的波纹系数，节数越多，带宽比越大；二项式响应具有最平坦的带内特性，但是带宽比远小于等波纹响应；带状线窄边耦合耦合器与微带线耦合器耦合性能几乎完全一致，论证了理论公式对于准TEM模的微带线近似完全可行。最后设计的微带线耦合器经实际测试与理论仿真相符，满足使用要求。

[1]InderBahl,Prakash Bhartia.Microwave Solid State Circuit Design,微波固态电路设计[M].北京：电子工业出版社.

[2]胡助明.宽带带状线定向耦合器的设计[J].

[3]A L Fel’dshtein.Synpaper of stepped directional couplers [J].Radiotekh.i Electron,1961,6(2):234-240.

[4]R Levy.General synpaper of asymmetric multi-element coupled-transmission-line directional couplers[J].

Design and Application of Wideband Directional Coupler

WANG Jiabo,CAO Xuesong
（Nanjing Electronic Device Institute,Nanjing 210016,China）

The paper analyses the coupled-transmission-line directional coupler.For the symmetric,the universal expression of multi-element directional coupler is obtained and then the couple coefficient of every element by the condition that the forward(n-1)steps derivative of Binomial response(the most flat response) is calculated.For the asymmetric,normalization impedance of step-impedance filter by Chebyshev polynomial and Richard transform are synthesized.This is the same as theeven mode impedance of multi-element asymmetric directional coupler,because the 1/4 wavelength coupler and 1/4 wavelength step-impedance filter are equivalent.Then the couple coefficient of Chebyshev response can be obtained.In thepaper,the two kinds couplers are designed,whose frequency is from 4 GHz to 20 GHz.The frequency response of Binomial response coupler is the most flat.The bandwidth ratio of Chebyshev response coupler is larger than Binomial response coupler.Finally,two-element micro-strip coupler made with Rogers 5880 micro-strip,0.254 mm thickness,is applied in module.

binomial response;Chebyshev response;wideband directional coupler

TN402

A

1681-1070（2016）11-0039-05

2016-6-20

王家波（1979—）,男，江苏连云港人，高级工程师，2001年毕业于南京理工大学电子工程与光电技术学院，获学士学位，现主要从事相控阵雷达收发组件研究工作；

曹雪松 (1984—)，男，江苏丹阳人，工程师，2006年毕业于东南大学信息科学与工程学院，2009年毕业于中科院紫金山天文台毫米波与亚毫米波实验室，获硕士学位，现主要从事相控阵雷达收发组件相关工作。