飞锯控制系统锯车位置和速度的测量方法

甄自源， 杨振强

(大连理工大学 电气工程学院，辽宁 大连 116023)



飞锯控制系统锯车位置和速度的测量方法

甄自源， 杨振强

(大连理工大学 电气工程学院，辽宁 大连 116023)

飞锯控制系统作为一种高精度管材切割系统，其精度和稳定性很大程度上取决于锯车位置和速度的测量精度和稳定性。基于以上需求，使用TMS320F28069处理增量式光电编码器发出的脉冲信号，提出了一种测量该系统锯车位置与速度的方法。该方法引入脉冲长度简化运算和操作，提高了更换设备时的效率，同时给出了锯车行进长度的计算公式。在测量锯车速度方面，优化M/T加权平均过渡法以保证测速能够平滑过渡，并通过误差分析和仿真验证了此方法的可行性，满足了系统对精度和稳定性的要求。

飞锯控制系统；脉冲长度；M/T加权平均过渡法

0 引言

飞锯控制系统可广泛用于管材、型材等生产线的高精度连续自动追踪切割，大幅提高生产效率。由于系统为动态在线切割，对位置与速度的精度要求较高[1]，因此能够准确测量锯车的位置和转速显得至关重要。该系统以DSP作为运动控制器，其中的eQEP(增强正交编码脉冲)模块能够高速采集光电编码器的脉冲信号，再对其进行处理和计算即可测量锯车的位置和转速，精确度与PLC控制相比大为提高。同时在计算转速时使用更加合理的算法，可以使高转速和低转速之间能够平滑过渡，进一步提高系统的稳定性。

1 飞锯控制系统概述

1.1 飞锯控制系统的组成

本文所述飞锯控制系统由以TMS320F28069处理器为核心的运动控制器、VFD-VE伺服型变频器、DOP-B05S100 触摸屏、锯车系统以及测速系统等组成，如图1所示。

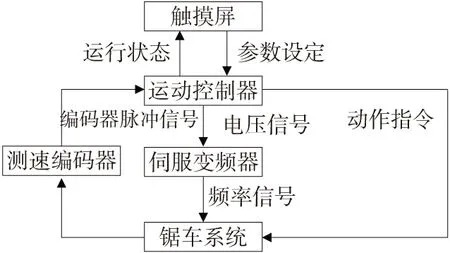
图1 飞锯控制系统组成框图

运动控制器对整个系统进行监视和控制。伺服型变频器接收运动控制器发出的电压信号转化为频率来调整锯车电机的转速。触摸屏可发出不同的动作指令，调整系统的部分参数，并显示系统的运行状态。锯车系统由可前后移动的锯车与固定轨道组成，锯车上装有锯片，并连接继电系统[2]，其机械结构示意图如图2所示[3-4]。继电系统用来下达夹紧、松夹、落锯、抬锯等动作指令。测速系统可实时测量各电机的转速，其中编码器选用的规格是24V，1000线的增量式光电编码器。

图2 锯车系统机械结构示意图

1.2 飞锯控制系统锯车的运动状态分析

在本系统中，需要测量以下四部分组件的速度：锯车行进速度、管行进速度、锯片转速和锯片主轴移动速度。锯车和管材的各阶段运动状态图如图3所示，其中T1为锯车加速阶段，T2为夹紧前锯车调整阶段，T3、T4、T5、T6分别为夹紧、落锯、抬锯、松夹阶段，T7为锯车回零点阶段，T8为锯车零点调整阶段[5]。

图3 锯车各阶段运动状态

理想状态下，管材匀速前进，锯车与管行进至两者行程差为设定的切割管长时，两者恰好同速，输出夹紧管材的信号再落锯切管；然而由于实际上管材并不总是匀速前进，且测量有误差，此时锯车与管可能不同速，但速度差最好尽量小。由此可见，锯车行进位置和速度的测量精度及稳定性尤为重要。

本系统管长设定范围为2m～6m，定尺精度为3mm，即切割后的管材与设定管材的误差最大值为±3mm。具体到各运动阶段来说，发送夹紧管材信号前定尺精度主要取决于管材与锯车相对位置的测量精度；在发送夹紧管材信号后至管材被夹紧(由于继电器有动作时间)时，定尺精度主要取决于管材与锯车相对速度的测量精度，此部分定尺精度系统要求为1mm。本文以锯车为例，提出其位置和速度的测量方法，又由于管材以匀速行进，则定尺精度以及系统稳定性主要取决于锯车位置和速度的精度和稳定性。

2 eQEP(增强正交编码脉冲)模块

TMS320F28069处理器的eQEP模块结合增量式光电编码器可实现获取运动控制系统位置、速度以及方向信息的功能[6]。

eQEP模块的QEPA和QEPB引脚为正交时钟模式输入引脚，可接收编码器输出的相差90°的方波信号。如图4所示，这一系列正交脉冲信号经由正交解码单元QDU解码后得到4倍频的位置脉冲信号和方向信号，再通过位置计数器进行脉冲计数得到QPOSCNT和QDIR的值，即为电机的位置信息和方向信息[7]。

图4 eQEP输入信号计数与方向解码

3 行进长度的测量

3.1 编码器位置变化的脉冲计数测量

本文主要关注的是锯车的行进长度。通过将光电编码器与电机相连，根据1.1节和1.2节所述就可对锯车位置进行测量，由于行进长度是和编码器的累积行程相关，而不用关注编码器的旋转周数，因此只需记录eQEP位置锁存器QPOSSLAT的值来确定编码器向前或向后行进了多少个QCLK脉冲。

3.2 脉冲长度的应用

若要计算锯车行进长度，除了记录编码器产生的脉冲计数值，还需要引入一个系数——脉冲长度，即编码器的一个脉冲可换算为多少长度。由于锯车系统结构不同，因此锯车脉冲长度Kc的计算方法也不同，如式(1)所示：

(1)

其中，Z为齿轮齿数，M为齿轮模数，X为编码器计数的倍频，P为编码器的每转脉冲数，I为减速箱传动比。本系统使用的76型飞锯齿数Z为25，模数M为8，锯车履带传动比I为7.1，锯车编码器为1000/rpm，4倍频，则代入上面公式计算得锯车脉冲长度Kc=0.0221mm。

由于锯车脉冲长度Kc均可通过触摸屏输入来随时更改，因此当系统的部分设备更换或有一定的磨损后，只需更改这个脉冲长度即可满足设备变化的要求，简化了计算和操作。

3.3 行进长度的计算

根据3.1和3.2节，可得到行进长度的计算公式，如式(2)所示：

L=CNT×K

(2)

其中，L为行进长度(前进方向为正)，CNT为eQEP位置锁存器QPOSSLAT的值，K为脉冲系数。式(2)也可应用在其他组件计算行进长度的情况。

由于每次测量行进长度时，脉冲计数值有±1个脉冲的最大误差，因此本方法在测量行进长度时的误差为1个脉冲对应的长度，即脉冲长度。同时为了避免系统长时间运行导致误差累积，锯车在完成一定次数切管后，返回起始位置时应对起始位置，即行进长度为0的点进行校正[8]。校正后的起始位置由限位开关确定。

4 锯车速度的测量

4.1 M/T加权平均过渡法测速的原理

M法和T法是电机转速测量的常用方法。其中，M法是指通过测量在一定时间间隔T1内编码器产生的脉冲数M1来计算转速的方法[9]。又由于本系统引入了脉冲长度，可将测量转速转化为测量脉冲频率f1(每秒产生的脉冲数)，故可得式(3)：

(3)

若使用DSP的eQEP模块进行M法测速，则需使能eQEP的UTO(单位超时)中断，通过设置单位周期寄存器QUPRD的值N1和系统时钟频率f0来确定T1，通过测量前后两次进中断时的位置计数锁存器QPOSLAT的差来确定M1。故式(3)可化为式(4)：

(4)

在某些极端情况下M1会有±1的误差，则在测量较高转速时M1的相对误差较小，而T1又为定值，因此M法在测量高速时误差较小[10]。

而T法是指通过测量编码器产生一定数量的脉冲M2所需要的时间T2来计算转速的方法。同M法，脉冲频率f2的计算公式如式(5)[9]：

(5)

若使用DSP的eQEP模块进行T法测速，则需检测eQEP的状态寄存器QEPSTS的单位位置时间标志位UPEVNT，通过设置捕捉控制寄存器QCAPCTL和单位位置事件预定标UPPS来确定M2，而T2通过对分频后的系统时钟脉冲进行计数的计数值N2来确定，其中时钟频率由系统时钟频率f0和捕捉定时器时钟预定标CCPS来确定，计数值由捕捉周期锁存器QCPRDLAT来确定。则式(5)可化为式(6)：

(6)

需要注意的是，eQEP的捕捉定时器发生上溢会导致锁存器QCPRDLAT的偏差较大，因此需要监测状态寄存器QEPSTS捕捉上溢标志位COEF，当该标志位为“1”时T2的值不能用于计算转速。

在某些极端情况下T2会有±1的误差，则在测量较低转速时T2的相对误差较小，而M2又为定值，因此T法在测量低速时误差较小[11]。

M法和T法分别适用于测量高速和低速的情况，若将转速以某一个值作为分界线来区分高速与低速，可能会出现M法和T法相互转换时转速突变的情况。根据这一情况，可采用M/T加权平均过渡法来进行测速，即在高速和低速时分别使用M法和T法测速，在测速误差接近需要切换时使用变系数加权平均法，使转速平滑切换，测量误差无波动，以提高系统的稳定性[12]。

M/T加权平均过渡法将电机转速分为三个区域，即高速区、低速区和过渡区，计算公式如式(7)所示：

f=sf1+(1-s)f2

(7)

其中，f为加权计算后的脉冲频率，与锯车脉冲长度相乘即为锯车行进速度，故后文均将f的误差率作为锯车速度的误差率；f1为M法测量的转速，s为其权值；f2为T法测量的转速，1-s为其权值。

s的计算方法有多种，文献[12]曾给出一种线性算法。基于该方法，可应用于飞锯控制系统的s的计算公式如式(8)所示：

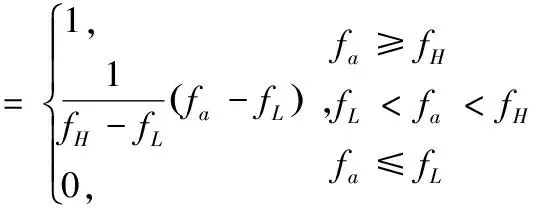
(8)

其中，fa是f1与f2的平均值，作为该时刻转速处在何区域的判断频率值，即fa=(f1+f2)/2；fH是高速区与过渡区的分界限转速值；fL是低速区与过渡区的分界限转速值。

该方法有一定的合理性，且计算简单，但还可以进一步优化，具体分析将在4.2节论述。

4.2 误差分析与仿真

由1.2节可知，在发送夹紧管材信号后至管材被夹紧时，定尺精度系统要求为1mm，定尺精度以及系统稳定性主要取决于锯车位置和速度的精度和稳定性。设ΔL为锯车行进长度测量误差最大值，δmax为测速误差率最大值，fmax为脉冲频率最大值，ΔT为夹紧继电器最大动作时间，则其计算公式如式(9)所示：

ΔL=δmaxfmaxKcΔT

(9)

其中，fmax为200kHz，ΔT为25ms。由3.2节Kc=0.0221可计算得，δmax=0.9%。故测速误差率不能超过0.9%。

为了使过渡区的转速平滑切换，测速误差不大于0.9%，则需保证过渡区的转速误差率函数连续，且函数值不大于0.9%。M法和T法的测速误差率分别如式(10)和式(11)所示[13]：

(10)

(11)

而过渡区的测速误差率如式(12)所示：

(12)

由于M法和T法的测速误差率函数都是单调的，因此同一转速下测速误差率也相同时的脉冲频率为测速误差分界点，即脉冲频率大于此频率时M法测速误差较小，而小于此频率时T法测速误差较小，故这个测速误差分界点应该在过渡区内。由式(13)即可算出该脉冲频率：

(13)

在本文的飞锯控制系统中，相关参数设置如下：f0=8MHz，N1=16000，UPPS=5，CCPS=4，计算可得测速误差分界点时的脉冲频率为89.2kHz。选取fH=100kHz，fL=80kHz，此时，若使用式(8)的线性算法s的取值计算公式如式(14)所示，相应函数图形如图5所示。

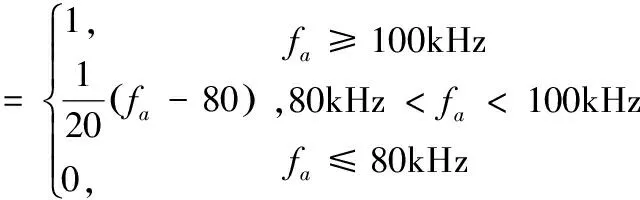
(14)

图5 权值线性算法函数图

高速区(M法)的误差率在脉冲频率为100kHz时为最大值0.5%，低速区(T法)的误差率在脉冲频率为80kHz时为最大值0.503%，而在过渡区，令fa=f，将式(14)代入式(12)可算出在该区域内以脉冲频率f(单位为kHz)为自变量的线性算法误差率函数如式(15)所示：

(15)

该函数的Matlab仿真图如图7虚线所示，该函数在(80,100)的区间内连续，且最大值约为0.56%。而本文提出M/T加权平均过渡法权值的另一种算法，s随fa以二次函数规律变化，简称为二次算法。该函数如式(16)所示，相应函数图如图6所示。

(16)

该方法在高速区和低速区的误差率与线性算法相同。令fa=f，将式(14)代入式(12)可得过渡区内以脉冲频率f为自变量的二次算法误差率函数，如式(17)所示：

(17)

二次算法的误差率函数仿真图如图6实线所示，图中脉冲频率处于(80,100)的区间为过渡区，

图6 权值二次算法函数图

其他区域分别对应低速区和高速区，即分别应用了T法和M法。由该图易知，该函数在过渡区内时连续，且最大值与一次算法的最大值相同。两种算法的结果最大的不同是，在除边界值和最大值处之外，二次算法的转速误差率均比线性算法的误差率低，并且在分界点80kHz和100kHz处，二次算法函数斜率与其他区域斜率连续，即转速误差率变化更加稳定，因此二次算法更加合理。

图7 过渡区内误差率仿真图

选用二次算法的M/T加权平均过渡法测速误差率如表1所示。由表1可知，本方法测速误差率最大值不超过0.6%，满足误差率连续且不大于0.9%的要求。

表1 M/T加权平均过渡法的频率分区和误差率表

5 结论

本文介绍了飞锯控制系统，以及测量其锯车位置和转速的精度和稳定度的重要性。同时介绍了DSP的eQEP(增强正交编码脉冲)模块测量该系统锯车行进长度和转速的的方法和计算公式。其中，引入脉冲长度可优化行进长度和转速的算法，简化设备更换或磨损后的操作，提高了效率；使用M/T加权平均过渡法来测速保证了高转速与低转速能平滑转换，且误差率不大于0.9%，同时对权值的计算方法进行了优化，使用更加合理的二次算法，进一步保证了系统的精度和稳定性。

[1] 王海鹏,陈和平,朱英韬,等. 工业机器人在板材切割生产线的应用[J]. 组合机床与自动化加工技术, 2015(5):141-144.

[2] 李平，杨晓明，牛骁. 飞锯机的控制方案简析[J]. 重型机械科技，2006(2):36-39.

[3] 于冬,顾培亮,高璇. 基于PLC技术的自动切管机控制系统的研究[J]. 组合机床与自动化加工技术, 2004(10):7-9.

[4] 任意，石小英，曾胜.全自动型材切割机设计与实现[J].电机与控制应用，2009(9)：30-33.

[5] Yuhua Zhang, Xinhuan Song.The Motion Control of Profile Milling Flying Saw[C] // MATEC Web of Conferences 2015. 2015 7th International Conference on Mechanical and Electronics Engineering, 2015, 31：03014p1- 4.

[6] Texas instruments. TMS320x2806x Piccolo Technical Reference Manual[S]. 2011，1：452-453.

[7] 王子博. 编码器四倍频电路的单片机高速算法设计[J]. 组合机床与自动化加工技术, 2007(11):73-74,78.

[8] 杨红波. 铜材自动定尺飞锯机控制系统的研究[D].大连:大连交通大学, 2010.

[9] 邓建，林桦. 基于DSP的绝对式光电编码器的电机转速测量[J].电机与控制应用，2010(1)：50-52,55.

[10] 苏指南. 仿形铣切飞锯的运动控制[D].天津:天津理工大学, 2011.

[11] 李昕奇，金勇. 基于DSP2812的电动机测速方法的研究[J]. 电气自动化，2011(4)：81-82.

[12] 张涛，杨振强，王晓旭. 应用eQEP及编码器测量电机位置与速度的方法[J]. 电气传动，2011(4)：48-51.

[13] 陈伯时. 电力拖动自动控制系统-运动控制系统[M]. 3版.北京:机械工业出版社，2006.

(编辑 李秀敏)

Method of Measuring Saw Car’s Position and Speed in Flying Saw Control System

ZHEN Zi-yuan,YANG Zhen-qiang

(College of Electrical Engineering, Dalian University of Technology, Dalian Liaoning 116023, China)

As a high precision pipe cutting system, accuracy and stability of flying saw control system depends largely on the accuracy and stability of the saw car’s position and speed. Based on the above requirements，introduced a method applied to this system to measure the saw car’s position and speed, which utilizes TMS320F28069 to process the pulse signals transmitted from incremental optical encoder. The method introduces pulse length to simplify the calculation and operation, which improves efficiency of changing instruments. The computational formula of moving length of the saw car is given. The method of M/T weighted average transition is optimized to guarantee smooth transition of measuring rotate speed, of which the practicability is proved by error analysis and simulation. The method meets the demand of accuracy and stability for the system.

flying saw control system; pulse length; M/T weighted average transition

1001-2265(2016)11-0100-05

10.13462/j.cnki.mmtamt.2016.11.027

2016-01-13

甄自源(1990—)，男，河北邢台人，大连理工大学硕士研究生，研究方向为电机控制，(E-mail)zhen_ziyuan@163.com；通讯作者：杨振强(1964—)，男，哈尔滨人，大连理工大学副教授，博士，研究方向为电机控制、模糊控制等，(E-mail)yangzq@dlut.edu.cn。

TH162;TG506

A