逻辑齿轮的建模及齿廓参数优化
金建军,王玉闯,刘德平
(1.合肥京东方显示技术有限公司,合肥 230012;2.郑州大学 机械工程学院,郑州 450001)
逻辑齿轮的建模及齿廓参数优化
金建军,王玉闯,刘德平
(1.合肥京东方显示技术有限公司,合肥 230012;2.郑州大学 机械工程学院,郑州 450001)
为了得到逻辑齿轮最优齿廓参数,首先根据逻辑齿条齿廓方程和逻辑齿条与逻辑齿轮之间相互啮合关系,求出逻辑齿轮齿廓方程。再通过matlab编程求出齿廓上的相对曲率为零的点的坐标,对其拟合画出齿轮轮廓。然后,基于同条件下的渐开线齿轮的齿顶厚,提出了一种齿廓参数优化方法。最后,通过对相同齿顶厚下的不同齿廓参数的特征对比,得出了应选初始压力角较小的一组齿廓参数。
逻辑齿轮;MATLAB;齿廓;参数优化
0 引言
日本学者小守勉首次提出了名为逻辑齿轮(Logix Gear)的新型齿轮。其节圆内外为凹凸形式,在啮合时齿廓上分布着大量相对曲率为0的结合点(即为NP点)[1]。这样构成的齿轮齿廓可以保证两齿轮在相互啮合时性能较好。赵韩等基于精确建模的微线段齿轮弯曲强度理论分析其中对微线段齿轮进行了建模[2],并未对逻辑齿轮节圆以外半部齿廓的建立做详细说明,因此将对此做补充并选取标准齿顶高系数等建出逻辑齿轮。刘红雨等的逻辑渐开线齿条齿廓方程的建立及参数的优化计算[3],没有对逻辑齿轮齿廓参数进行优化,而逻辑齿廓参数对逻辑齿轮的弯曲强度和接触性能等影响显著。因此本文基于同条件下的渐开线齿轮的齿顶厚,提出了一种新的逻辑齿轮齿廓参数的优化方法。最后依据此方法对不同齿廓参数的特性对比,得出了最优齿廓参数。
1 逻辑齿轮模型的建立
逻辑齿轮的形成是基于逻辑齿条,与逻辑齿条相互啮合的共轭轮廓便是逻辑齿轮的轮廓。除了与渐开线齿轮共有的参数外,与逻辑齿条形成有关的参数还有:初始基圆半径G0、初始压力角α0以及相对压力角δ等。首先根据逻辑齿条的形成原理,得到逻辑齿条一侧齿廓节线以上半部的齿廓方程(如式(1))和节线以下半部的齿廓方程(如式(2))。然后,根据逻辑齿条与逻辑齿轮节圆以内部分齿廓的啮合过程,逻辑齿轮一侧齿廓节圆以内半部的齿廓方程(如式(3))[4]。
(1)
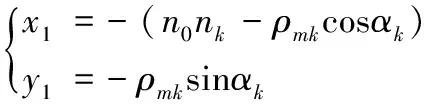
(2)
(3)
其中,r2为逻辑齿轮节圆半径。
取m=4,ha*=1和c*=0.25,齿条的齿厚s和齿间宽e都等于πm/2。相关齿廓参数取初始压力角α=6.0°,相对压力角δ=0.05°,初始基圆半径G0=10000mm[5],取基圆半径变化规律Gi=G0[1-sin(0.6αi)],根据式(1)和式(2)画出逻辑齿条图,如图1所示。

图1 逻辑齿条齿形
根据逻辑齿条1段齿廓方程(如式(3))和其与逻辑齿轮节圆以外半部啮合过程(如图2),可推导出逻辑齿轮节圆以外半部的齿廓方程,如式(4)。

图2 逻辑齿条与逻辑齿轮上半部啮合过程
(4)
取逻辑齿轮齿数z=30,首先根据式(3)和式(4)用matlab 编程求出逻辑齿轮一侧齿廓上所有的NP点横坐标和纵坐标,再编辑成坐标点形式,并在AutoCAD中用拟合命令对所有NP点进行拟合,画出逻辑齿轮一侧齿廓曲线。然后镜像出单个轮齿上另一侧齿廓线,得到一个完成的轮齿,再圆周均布出所有轮齿齿廓[6]。最后对整个齿轮进行完善,得到完整的逻辑齿轮二维图[7],如图3 所示。
最后,对上述逻辑齿轮二维图进行拉伸,可以得到其三维模型(未列出)。
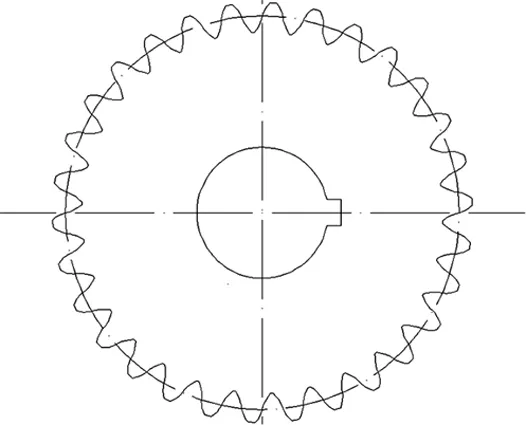
图3 逻辑齿轮二维图
2 逻辑齿轮齿廓参数优化方法
逻辑齿轮的设计可参考同条件的渐开线齿轮,因此,为了保证最终设计逻辑齿轮齿顶的弯曲强度,要求逻辑齿轮的齿顶厚应和同模数同齿数的渐开线齿轮相近[8],齿顶厚计算比较复杂,但可用齿廓顶点(x,y)与Y坐标轴的夹角代替,齿顶厚与夹角c成反比,但是一一对应的关系,如图4中c所示。其中夹角c=arctan(x/y)。

图4 齿顶厚与夹角c示意
在满足了齿顶厚之后,需要考虑逻辑齿轮齿根的弯曲强度以及啮合时接触强度。如图5所示,其为逻辑齿轮齿轮轮齿的受力分析。当在轮齿顶部施加一定载荷时,轮齿根部的弯曲应力大小取决于齿顶圆压力角。因为切向力Ft=Fcosα,所以齿顶圆压力角α越大,根部的弯曲应力越小[9]。而逻辑齿廓上逻辑点数多少直接影响啮合时接触性能好坏。

图5 逻辑齿轮轮齿的受力分析
在满足同样齿顶厚的逻辑参数中,有许多种组合,因此需要从中找到合适的一组,使齿顶圆压力角最大,而且逻辑齿廓上逻辑点数也相对较多,或者是逻辑齿廓上逻辑点数最多,齿顶圆压力角也相对较大。
3 逻辑齿轮齿廓参数优化流程
为了便于计算和加工,我们一般取相对压力角δ=0.05°。初始压力角的范围一般在2°~12°之间[5],因此在此范围内每隔2°取一个值,总共取出6个初始压力角的值,分别计算得到其对应下满足和同条件渐开线齿轮齿顶厚相接近的初始基圆半径的值,同时计算出每一组参数下的齿顶圆压力角和逻辑齿廓上NP点数。对相同齿顶厚下几组不同齿廓参数的特性进行对比分析,最后从中选出合适的逻辑参数。
计算程序流程如图6所示,表示含义为首先选择一组初始的逻辑参数,计算得到其齿顶圆处夹角c,并与同条件下渐开线齿轮c1相比较,如果逻辑齿轮较大,那么对初始基圆半径G0进行增大[10],进行循环直到两者相接近;反之,则对初始基圆半径G0进行减小,同样进行循环直到两者相接近,就可以得到此初始压力角对应下的初始基圆半径。然后再对初始压力角进行增大,每次增加2°,同上述步骤,同样可以得到对应条件下的初始基圆半径。这样就得到了初始压力角2°~12°之间每隔2°对应的初始基圆半径。上述计算初始基圆半径的同时,还需要计算出此条件下对应的齿顶圆压力角以及逻辑齿廓节圆以上NP点数目。最后把每一种逻辑参数下得到的结果列在表中进行比较分析,如表1所示。

图6 优化流程图

α/°G0/mmαa/°NP点数2596036.133434852034.5530761151032.7626981525031.07232102031029.37195122785027.58157
由上表可看出,在同样的齿顶厚和相对压力角下,随着初始压力角的减小,初始基圆半径也要相应减小,但是齿顶圆压力角增大,逻辑齿轮根部弯曲应力较小,而且齿廓上NP点数目增多,接触性能变好。
4 结论
(1)在相对压力角确定的情况下,若逻辑齿轮要满足和同条件下渐开线齿轮相接近的齿顶厚,初始压力角和初始基圆半径之间要选择合适的组合,也即是随着初始压力角的选择增大,初始基圆半径也要相应增大至适当值。
(2)为了保证逻辑齿轮有足够的弯曲强度和接触强度,需要选择齿顶圆压力角较大而且齿廓上NP点数目较多者,因此应选择初始压力角为2°的那一组齿廓参数。
[1] T Komori, Y Ariga , S Nagata.A new gears profile having zero relative curvature at many contact points (logix tooth profile)[J]. Journal of Mechanical Design ,1990(3):430-436.
[2] 赵韩,陈奇,黄康.基于精确建模的微线段齿轮弯曲强度理论分析[J].组合机床与自动化加工技术 ,2010(7):62-64.
[3] 刘红雨,任传胜,赵韩,等.微段渐开线齿条齿廓方程的建立及参数的优化计算[J].甘肃工业大学学报, 2003,29(3) :54-56.
[4] 刘红雨. 逻辑齿轮的原理及强度研究[D].合肥:合肥工业大学,1994.
[5] 王爱群.LogiX齿轮啮合理论及其创成加工技术研究[D].济南:山东大学,2003.
[6] 谢 飞 ,黄 旭,王建华 ,等.基于UG的Logix齿轮参数化建模及弯曲应力分析[J].机械传动,2011,35(3):30-32.
[7] 张训福,黄康,陈奇.渐开线齿轮齿根过渡曲线方程的建立[J].组合机床与自动化加工技术,2008(2):1-3.
[8] 刘红雨,赵韩,梁锦华.微线段齿轮的齿廓参数选择及几何尺寸的计算[J].机械传动,2001,25(4) :27-28.
[9] 刘红雨,赵韩,梁锦华.微段渐开线齿轮接触强度与弯曲强度的分析[J].上海理工大学学报,2003,25(3):277-280.
[10] 冯显英,王爱群, 李剑锋.LogiX齿轮的性能研究[J].机械传动,2003,27(5):8-10.
(编辑 李秀敏)
Modeling and Analysis and Optimization of Parameters of the Tooth Profile of the Logix Gear
JIN Jian-jun1,WANG Yu-chuang2,LIU De-ping2
(1.Hefei BOE Display Technology Co. Ltd., Hefei, 230012; 2.School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001,China)
In order to get the optimal parameters of the tooth profile of the logix gear,firstly, according to the equation of the tooth profile of the logix rack and the relationship which the logix rack and the logix gear is meshed, the equation of the tooth profile of the logix gear is obtained. Combined with the equation of the tooth profile of the logix gear, the coordinates of the points which relative curvature is zero at the tooth profile are calculated by matlab programming, which are fitted to draw out the outline of the gear. Then,based on the tooth thickness of the addendum circle of the involute gear under the same condition, a method to optimize the tooth profile of the logix gear is promoted. Finally, by comparing to the characteristics of different tooth profile parameters under the same tooth thickness of the addendum circle, it is concluded that parameters of the tooth profile of the smaller initial pressure angle should be adopted.
logix gear;MATLAB;tooth profile;parameter optimization
1001-2265(2016)11-0038-03
10.13462/j.cnki.mmtamt.2016.11.011
2015-12-13;
2016-01-17
金建军(1990—),男,河南沈丘人,合肥京东方显示技术有限公司工程师,硕士,研究方向为CAD/CAM,(E-mail)15538087359@163.com。
THl32;TG506
A

