基于自抗扰控制器的永磁同步电主轴速度扰动控制研究

孙荣俊，孙中圣，鲁 明

(1.南京理工大学 机械工程学院，南京 210094； 2.北京控制工程研究所 机电中心，北京 100086)



基于自抗扰控制器的永磁同步电主轴速度扰动控制研究

孙荣俊，孙中圣，鲁 明

(1.南京理工大学 机械工程学院，南京 210094； 2.北京控制工程研究所 机电中心，北京 100086)

针对传统永磁同步电主轴(PMSS)调速系统在外部扰动或不确定参数变化等状况下的速度控制性能不佳的问题，提出了速度环ADRC调节器的控制策略，该方法利用扩张状态观测器(ESO)对系统中的内外部“总扰动”进行估计及补偿，并利用非线性状态误差反馈控制器(NLSEF)对跟踪微分器(TD)的过渡过程与ESO产生的状态估计的误差进行非线性组合，实现优于经典PI调节器的线性组合的控制效果。仿真结果表明：在该控制策略下，PMSS具有良好的动态响应性能以及较强鲁棒性。

永磁同步电主轴;速度环;自抗扰控制器

0 引言

电主轴将电机内装于主轴本体内，具有结构紧凑、动态特性好的优点。它的应用实现了机床的“零传动”，同时也改善了机床动平衡、减小了振动和噪声[1]。随着钕铁硼等永磁材料成本的下降，加上永磁同步电主轴(permanent magnet synchronous spindle，PMSS)在性能和结构方面的优势，PMSS势必成为高端机床中的应用趋势。

PMSS与永磁同步电机的驱动控制策略基本相同。PMSS调速系统可以近似为一阶积分型线性系统[2]，在其通常使用的矢量控制器中，速度环调节器大都采用PI调节器，而经典PI调节器存在以下劣势[3]：对增益的变化很敏感，存在“快速性”和“超调”的矛盾，积分反馈易造成振荡和积分饱和。

PMSS是一个非线性、强耦合、参数时变的系统，当系统模型参数存在摄动或存在外部扰动，经典PI调节器的控制性能就显得不尽人意了。为此不少学者就具有高动、静态性能和鲁棒性的速度环调节器做了不少研究。刘颖等人在滑模变结构控制的基础上引入积分补偿和扰动观测器环节[4]，鲁文其等人提出了抗扰动自适应控制[5]，这两种控制策略都具有较好的动静态性能和鲁棒性，但都依赖于精确的系统模型。毋华丽提出了一种基于哈密顿系统理论的双环路鲁棒控制方法，提高系统对负载扰动的鲁棒性[6]，但系统设计过于繁琐。Nga Thi-Thuy Vu等人提出了一种基于确定性等价原理的鲁棒自适应速度控制器，该控制器不需精确知道系统模型参数且能快速适应系统参数和负载转矩变化[7]。Z·Hashemi等人提出了一种抗积分饱和的PI调制器，并利用遗传算法对该控制器的参数进行训练及优化[8]，但该方法计算量大，实时性较差。

本文针对PMSS运行过程中由于负载转矩、摩擦系数以及转动惯量等参数摄动和外部不确定扰动造成的系统性能下降的问题，设计了速度环自抗扰控制器(Active-Disturbance Rejection Controller，ADRC)，其能够有效地对系统内外扰动进行估计并加以补偿，且不依赖于系统模型[9]。

1 PMSS数学模型

为简化PMSS的数学模型，首先作如下假设：

(1)忽略铁心饱和及磁滞损耗；

(2)不考虑转子的阻尼效应；

(3)相绕组中感应电动势波形为正弦波；

(4)电机参数不受影响。

则PMSS在d-q轴下的电压方程和转矩方程可分别表示为式(1)和式(2)：

(1)

(2)

忽略系统的静摩擦和库伦摩擦，只考虑黏性摩擦，易知PMSS的运动方程可表示为式(3)：

Te=Jpwr+Tl+Rwr

(3)

式中:ud,uq，id,iq，Ld,Lq分别为d-q轴下的定子电压，电流，电感；we,wr分别为转子的电角速度和实际角速度；Ψf为永磁体磁链；RS为定子电阻；p为微分算子；Te为电磁转矩；Pn为极对数；J为转子和所带负载的总转动惯量；Tl为负载转矩；R为粘滞摩擦系数。

2 自抗扰控制器

自抗扰控制器(ADRC)是一种非线性控制器，其标准结构包含三个子模块：跟踪微分器(Tracking Differentiator, TD)，扩张状态观测器(Extended State Observer, ESO)[10]，非线性状态误差反馈控制器(Nonlinear State Error Feedback, NLSEF)[11]。图1是一个常用二阶ADRC的结构示意图。

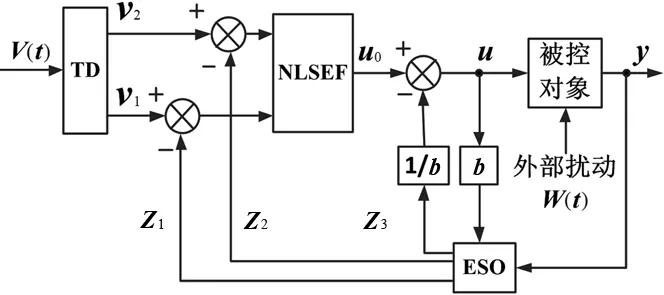
图1 二阶ADRC结构框架

2.1 跟踪微分器(TD)

如图1所示，TD将输入信号v(t)处理后，输出对应的跟踪信号v1和一阶微分信号v2。这样，当输入信号为突变信号时，经过TD的处理可提供光滑而连续的输出信号作为输入，并送进控制器，使得系统不会因为受到突变的输入信号而出现超调。TD对输入信号安排了合适的过渡过程，减小了初始误差，解决了超调与快速性的矛盾。常用二阶非线性跟踪微分器的一般形式如式(4)所示:

(4)

其中：

(5)

2.2 扩张状态观测器(ESO)

ESO是ADRC的核心，其品质很大程度上决定了ADRC的性能。如图1所示，ESO只用到原对象的输入和输出(即u和y)，是独立于描述对象传递关系的具体形式[3]，所以其不依赖系统模型。ESO可跟踪被控对象的各阶次状态变量z1、z2、z3，对来自系统内部和外部未知的各种扰动作用进行估计及补偿。常用三阶非线性扩张状态观测器如式(6)所示:

(6)

其中：

(7)

2.3 非线性状态误差反馈控制器(NLSEF)

NLSEF是一种广义非线性的PID控制器，其常用二阶非线性状态误差反馈控制率如式(8)所示。如图1所示，NLSEF将TD的过渡过程(v1、v2)与ESO产生的状态估计(z1、z2)的误差(ε1、ε2)进行非线性组合，结合ESO的扰动估计量的补偿来产生实际控制信号u，具有小误差大增益，大误差小增益的优点[12]。

(8)

ESO中的状态变量Z3用来跟踪扰动总和a(t)，利用其进行扰动补偿，可得到实际的控制量u。

u=u0-z3/b

(9)

3 ADRC在PMSS中的应用

3.1 基于ADRC的速度环设计

由PMSS的运动方程(式(3))推导可得到转速的一阶微分方程：

(10)

设计速度环时，将系统的转速wr作为目标输出y，d-q轴下的电流iq作为控制量输入u，状态变量x用于跟踪转速wr，令a(t)=1.5Pn(Ld-Lq)idiq/J-Tl/J-Rwr/J，b=1.5PnΨf/J，则PMSS速度环的状态方程可表示为：

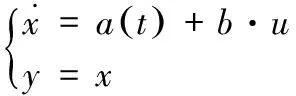
(11)

由自抗扰控制技术理论可知，PMSS转速的总扰动a(t)来自于内部模型扰动1.5Pn(Ld-Lq)idiq/J及外部扰动-Tl/J-Rwr/J。由于本文的研究对象为隐极式PMSS(Ld=Lq)，所以不存在内部模型扰动，即式(10)可简化为式(12):

(12)

此外，参数b理论上由电机参数计算得到，但与电机实际模型参数存在误差，用b0对模型参数b进行近似估计，将b0与b的误差作为一种扰动，利用ESO对其进行估计及补偿。因此总扰动为a(t)=-Tl/J-Rwr/J+(b-b0)u，反映了由负载转矩、摩擦系数以及转动惯量等参数摄动和不确定扰动[3]，其中负载突变影响最大。由此，可以构建基于ADRC的速度环调节器，其结构框架图如图2所示。

图2 一阶速度环ADRC结构框架

由于本系统为一阶的，因此在设计ADRC调节器时，取消了TD模块，直接将参考速度送给ADRC调节器。具体ADRC各模块表示如式(13)、式(14)所示:

ESO：

(13)

NLSEF：

(14)

3.2 ADRC的参数整定

ADRC的参数整定采用分离性原理[3-12]。

(1) ESO中的参数：β01，β02，α01，δ01，b0

其中β01，β02是ESO中的反馈增益，类似于PID参数中的P参数，其取值越大响应速度越快，但过大会产生超调和震荡，因此其整定时首先要保证ESO的稳定。α01和δ01是fal(e,α,δ)函数的参数，α01为非线性参数(α01=1时，为线性函数)，初始值一般取0.5，然后再进行微调，δ决定fal(e,α,δ)函数的线性区域的宽度，过大会使得控制器只能工作在线性区域，起不到非线性反馈控制的目的，过小会出现颤振的问题。b0是模型参数b的近似估计值，作为可调参数进行调整，b0越大响应速度越快，但过大会导致超调及震荡。

(2) NLSEF中的参数：β11，α11，δ02，b0

NLSEF中的参数整定方法与ESO中的参数整定策略对应相一致，b0同上。

4 仿真与分析

根据ADRC控制器原理，结合PMSS数学模型设计了PMSS一阶ADRC速度环调节器，利用S函数构建了ADRC以及利用Simulink框图模块建立了PMSS驱动系统仿真模型，具体仿真模型如图3所示。仿真参数如下：PMSS的额定速度n=2200rpm，Pn=4，RS=0.13Ω，L=0.0015H，Ψf=0.1821Wb，J=0.00333kg.m2。直流母线电压Udc=300V，逆变侧调制周期TS=0.0002s。ADRC的参数分别为：ESO中的α01=0.11、δ01=0.01、β01=7、β02=5000，NLSEF中的α11=0.505、δ02=0.01、β11=0.008，b0=164。

图3 基于ADRC控制器的PMSS仿真模型

仿真内容包含：①转速由0～1000rpm的阶跃响应仿真；② 0.02s时刻突加负载(10N·m)的速度响应仿真。

0到1000rpm的阶跃响应的仿真结果如图4、图5所示，可以看出经典PI调节器下的阶跃响应出现了超调(4.2rpm)，调节时间(速度上升到稳态值的±2%误差范围所需要的最小时间)为0.0121ms，稳态误差为0.6rpm；而使用ADRC时，系统无超调，调节时间为0.011ms，稳态误差为0.3rpm。对比而言，ADRC具有更优的动静态特性。

突加负载(10N·m)的转速响应的仿真结果如图6所示，图7、图8分别为突加负载的转速响应曲线的局部放大图，可以看出使用经典PI调节器时，突加负载的瞬间，速度有一个6.4rpm的下降，且速度恢复时间很长，这是由于原来的PI参数是针对突加负载前的工况进行整定的，突加负载后已不适应，这也说明了其闭环动态品质对PI增益的变化很敏感。使用ADRC时，起初有一个3.5rpm的速度跌落，但之后迅速恢复到设定值。对比而言，在外部扰动的情况下，采用ADRC的系统有更小的速度变化和恢复时间，可更好地抑制因负载突变所带来的影响，因此ADRC具有更强的鲁棒性。

图4 阶跃响应(0～1000rpm)

图5 阶跃响应局部放大图

图6 突加负载的转速响应(10N·m)

图7 突加负载的转速响应图的局部放大图I

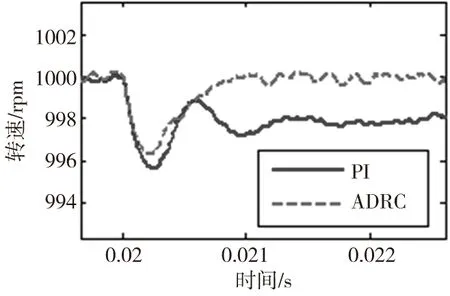
图8 突加负载的转速响应图的局部放大图II

5 结论

本文在分析速度环PI调节器不足的基础上，利用自抗扰控制技术设计了速度环ADRC调节器，建立了一阶速度环ADRC模型，并对其进行了仿真与分析。仿真结果表明，本文提出的速度环ADRC调节器相较于经典PI调节器具有更好的动静态特性及更强的鲁棒性。此外，ADRC的待整定参数相对较多，虽可以利用独立性原则按照一定的规律进行参数整定，但需要相对较深的理论基础和经验，所以ADRC的参数整定是一个难点。但还是有一些ADRC参数整定的优化方法的，如基于CPSO的ADRC参数整定法[13]，基于遗传基因算法的ADRC参数整定法[14]，基于粒子群优化算法的ADRC参数优化[15]等。总之，利用整定好参数的ADRC调节器可以获得比经典PI调节器更佳的性能。

[1] 杨贵杰,秦冬冬. 高速电主轴的关键技术及发展趋势[J].伺服控制,2010(2):34-36.

[2] 刘志刚,李世华. 永磁同步电机的二阶自抗扰控制算法

[A].第二十六届中国控制会议论文集[C].中国自动化学会控制理论专业委员会,2007:68-71.

[3] 韩京清. 自抗扰控制技术：估计补偿不确定因素的控制技术[M]. 北京：国防工业出版社,2013.

[4] 刘颖,周波,方斯琛. 基于新型扰动观测器的永磁同步电机滑模控制[J].中国电机工程学报, 2010,30(9):80-85.

[5] 鲁文其, 胡育文, 梁骄雁, 等. 永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(7):75-81.

[6] 毋华丽. 基于哈密顿系统理论的永磁同步电动机鲁棒控制[D].郑州:郑州大学,2013.

[7] Nga Thi-Thuy Vu, Han Ho Choi,Jin-Woo Jung. Certainty equivalence adaptive speed controller for permanent magnet synchronous motor[J]. Mechatronics,2012, 22(6):811-818.

[8] Hashemi Z, Mardaneh M, Sha Sadeghi M. High performance controller for interior permanent magnet synchronous motor drive using artificial intelligence methods[J]. Scientia Iranica,2012,19(6):1788-1793.

[9] 刘丽英,许镇琳,梅强. 基于线性自抗扰控制器的异步电机调速系统[J]. 组合机床与自动化加工技术,2009(5):56-60.

[10] 韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策,1995,10(1):85-88.

[11] 韩京清. 非线性状态误差反馈控制律—NLSEF[J]. 控制与决策,1995,10(3):221-225.

[12] 刘清. 基于自抗扰控制器的永磁同步电机伺服系统控制策略的研究及实现[D].天津:天津大学,2011.

[13] Liu Chunfang, Zang Bin. Application and the parameter tuning of ADRC based On CPSO[C]. Chinese Control and Decision Conference, 2012:3277-3281.

[14] Zeng Wenfei, Yan Ling. The parameter setting and application study of ADRC based on immune genetic algorithm[C]. in 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems, 2010:183-186.

[15] Ping Wang, Hua Wang, Guoyu Bai, et al. Parameter Optimization of ADRC for Spacecraft Attitude Maneuver Based on Particle Swarm Optimization Algorithm[C]. in Sixth International Conference on IHMSC, 2014:194-197.

(编辑 李秀敏)

Study of PMSS Speed Disturbance Control Based on ADRC

SUN Rong-jun1，SUN Zhong-sheng1，LU Ming2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.Mechanical and Electrical Center, Beijing Institute of Control Engineering, Beijing 100086, China)

The control performance of traditional drive system of the permanent magnet synchronous spindle(PMSS) is poor when there is an external disturbance or an uncertain parameters changing, so the control strategy of speed-loop ADRC regulator is proposed. In this method, the total disturbance of the system is estimated and compensated by using ESO; and nonlinear combination of the errors is done by NLSEF. The simulation results show that the PMSS has good dynamic performance and strong robustness by this control strategy.

PMSS; speed-loop; ADRC

1001-2265(2016)11-0108-04

10.13462/j.cnki.mmtamt.2016.11.029

2016-01-15

国防科工局军用技术推广科研项目(科工技[2014]750)

孙荣俊(1990—)，男，江苏兴化人，南京理工大学硕士研究生，研究方向为永磁同步电机驱动技术，(E-mail)rongjun.sun@foxmail.com。

TH164;TG506

A