激光熔覆滚珠丝杠进给系统热特性有限元分析

路华伟，李 虎

(东北大学 机械工程与自动化学院，沈阳 101819)



激光熔覆滚珠丝杠进给系统热特性有限元分析

路华伟，李 虎

(东北大学 机械工程与自动化学院，沈阳 101819)

伴随着激光快速成型技术的快速发展，在精密加工过程中，研究进给系统的热特性能够确保加工产品的表面质量。文章以激光熔覆进给系统的滚珠丝杠为研究对象，在ANSYS中使用的移动热源模拟实际过程中的摩擦热，结合外界环境的温升过程，激光热源和空气对流的影响，对滚珠丝杠做了间接热—结构耦合分析，得出了在不同时刻下的温度场分布和热变形。结果表明滚珠丝杠在加工过程中所受温度和应力做相似的变化，即滚珠丝杠的温度和应力变化都呈现出波浪式上升的规律。

激光熔覆；滚珠丝杠；有限元法；温度场；热特性

0 引言

伴随着激光快速成型技术的快速发展，对其要达到的加工精度的要求越来越高，然而在激光成型过程中会产生大量的热量，进给系统受到这些热量的影响导致温度上升，产生热变形，从而影响了激光快速成型的加工精度[1]。大部分国内外学者从研究金属材料的性质出发，通过研究熔池特点来控制表面加工质量。但对于高精密加工来说，尤其是制造加工精度很高的军工产品，不仅要从表面塌陷这一方面来提高加工零件的表面质量，还要考虑机器本身在运功过程中产生的变形对加工工件质量的影响。

通过查阅文献资料了解了激光熔覆加工过程中的外界环境的温度变化，根据传热学知识确定了进给系统的热边界条件，考虑了运动过程中摩擦热的移动过程，本文采用有限元方法,在ANSYS中使用的移动热源模拟实际过程中的摩擦热，考虑了外界温度环境的温升过程，通过以上两处的热源和空气对流的影响，对滚珠丝杠的温度场和应力场进行分析。所得结果对激光熔覆进给机构误差补偿具有一定的参考价值。

1 热特性分析的理论基础

1.1 导热基本定律

傅里叶导热定律的文字表述:在导热过程中，单位时间内通过给定截面的热量，正比于垂直于该截面方向上的温度变化率和截面面积，而热量传递的方向却与温度升高的方向相反[2], 即：

(1)

其中：

(2)

式中:q′是热流密度, W/m2；比例常数λ是导热系数,W/(m·℃)；t是物体的温度，℃；n是等温面法向；λx,λy,λz是材料沿方向x,y,z上的导热系数；nx,ny,nz是等温面沿x,y,z方向上的分量；x,y,z是笛卡尔坐标的3 个方向轴。

1.2 牛顿冷却公式

当物体表面与周围存在温度差时，单位时间从单位面积上散失的热量与温度差成正比[3 ]。

q′=h(tS-tB)

(3)

式中:h是热传递系数， W/(m·℃)；tS是物体的表面温度，℃；tB是周围环境的温度，℃。

1.3 热变形的基本方程

假设有一个各向同性的立方体, 它在长、宽、高3个方向产生的热变形随温度的变化关系为[4]：

ΔL=αL0Δt

(4)

式中:ΔL是物体的变形量；L0是物体原尺寸；Δt是物体的温度变化值;α是材料线膨胀系数。

2 有限元模型的建立和边界条件的确定

2.1 滚珠丝杠有限元模型的建立

对进给系统进行ANSYS分析时，在不影响模型精度的前提下，对滚珠丝杠模型进行适当的简化修改：

(1)将直线滚珠丝杠中的圆角、倒角以及小尺寸的孔忽略不计。

(2)对于丝杠上的螺纹，其结构比较复杂，可将其忽略不计，将丝杠等效为光杠。

从而得到的滚珠丝杠的横截面尺寸如图1所示。在ANSYS软件中建立的模型如图2所示[5]。

图1 滚珠丝杠截面尺寸(单位：mm)

图2 滚珠丝杠有限元模型

2.2 相关参数的选择和计算

2.2.1 轴承的摩擦热

滚动轴承摩擦热从理论上分析，是由自身的摩擦力矩产生的，其热量传递到丝杠的轴端，使丝杠受热温度升高。其表达式为[6]：

Q=2pnM/60

(5)

M=M0+M1

(6)

式中，n为丝杠的转速，r/min；M称为滚动轴承的摩擦力矩，N·m；M0为与轴承类型、转速有关的力矩；M1为轴承所承受载荷相关的摩擦力矩。

2.2.2 滚珠丝杠螺母副的摩擦热

丝杠螺母副的载荷等效于推力角接触球轴承的载荷，珠丝杠相当于滚动的内圈，螺母相当于外圈，故其发热原理和滚动轴承的发热原理基本相同，故其摩擦生热的表达式仍可由式(4)表示，摩擦力矩M为：

M=Md+0.94Mp

(7)

Md=FdP2ph

(8)

MP=FPP2ph(1-h2)

(9)

式中，Md为驱动摩擦力矩；Mp为预紧力的阻力矩；P为丝杠的导程；Fd为丝杠螺母所受的轴向力；Fp为丝杠螺母所受轴向预紧力；h为丝杠螺母所具有的传动效率。

2.2.3 滚珠丝杠的对流换热

热对流有自然对流和受迫对流这两种方式，根据加工环境，丝杠以一定速度旋转，且丝杠上还带有螺纹，均会加快与空气的对流，即属于受迫对流。根据努谢尔准则, 换热系数h 的计算公式如下[7]：

(10)

式中:Nu为努谢尔特数；L 为特征尺寸。从式中可以看出只要解出努谢尔特数，便可求解出相应的对流换热系数h。对于滚珠丝杠的螺纹外表面，可以把其等效为螺旋管道的内表面，即把丝杠外表面的对流换热假定为螺旋管道管内的受迫对流换热，螺旋管道的曲率半径为滚珠丝杠的半径，管的直径等效为滚珠的直径。其中计算努谢尔特数的公式如下：

(11)

(12)

式中：εR为修正系数；Re为雷诺数；Pr为普朗克常数；d为管道直径；l为管道长度；Tf为流体温度；Tw为壁温。

2.2.4 空间热源的辐射

把空间热源假定为温度恒定的气体热源，因此空间热源与滚珠丝杠之间的辐射属于气体与外壳间的辐射传热。把滚珠丝杠外表面当做灰体，则空间热源和外壳表面之间反复进行着吸收和反射，滚珠丝杠外壳表面从空间热源辐射中吸收的总热量：

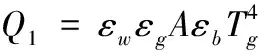
(13)

空间气体从滚珠丝杠外表面辐射中吸收的总热量为：

(1-αg)2(1-εw)2+…]

(14)

式中，εg表示温度为Tg时气体的发射率；αg表示温度为Tg的气体对来自于温度为Tw的外表面辐射的吸收率；

σb=5.67×10-8W/(m2·K4)称为黑体辐射常数；A为外表面总面积。

由本节公式可求出两端轴承转动产生的热量为18W/m2，丝杠吸收的摩擦热为1460W/m2，丝杠表面的对流换热系数为18W/(m2·k)，空间热源与丝轨的辐射传热量为174W/m2。

2.3 计算结果与分析

对滚珠丝杠分析前，依然做以下假定[8]：

(1)室温温度为20℃，材料物理参数如表1所示。

(2)丝杠的转速为30γ/min，且在丝杠旋转副和两端轴承所产生的热量有一半被丝杠吸收。

表1 材料部分物理参数

不同的轴承支承方式对滚珠丝杠的热分析结果也有所不同。当轴承的支承方式为一端固定，另一端游动支承时，其固定轴承对丝杠的热影响较大。当支承方式为两端支承时，两个轴承对丝杠都有影响。本文中选择支撑方式为一端固定、一端游动支承。固定端可承受轴向力和径向力，而游动端之可承受径向力，且可以微量的轴向跳动。固定端轴承采用直推轴承和深沟球轴承，游动端直采用深沟球轴承，当丝杠受热时，可以向游动端微量伸缩[9]。

取滚珠丝杠中心为坐标原点(0,0,0)，根据实验情况，空间热源的中心坐标为(0,500,0)。采用高阶耦合单元8节点SOLID278单元和表面效应单元SURF152，得到丝杠的温度场和应力场[10]。

由以上所计算出的热载荷以及边界条件，对丝杠进行了3400s的仿真计算，得出了在该时间段内的温度场如图3和应力场如图4[11]。

图3 1600s时刻的温度分布

图4 3400s时刻的温度变化

从图3～图6中可看出滚珠丝杠的温度最高值为23.5℃，最大温升为3.5℃，最大热变形为3μm。

以丝杠远离电机的轴端中心为原点坐标(0,0,0)，在丝杠表面上取三个点A1，A2，A3，其坐标依次为(0,20,200)，(0,20,600)，(0,20,1000)，得到该三点随时间变化的温度曲线如图5和应力曲线如图6所示。

图5 1600s时刻的应力分布

图6 3400s时刻的应力分布

图7 所选点的温度时间变化

图8 所选点的应力时间变化

从图7可以看出，该三点的温度变化曲线形状大致相似，呈现出波浪式上升的规律，而且由于轴承固定方式的不同，可看出丝杠靠近轴承固定端的温度比远离处的要高。从图7和图8中可看出应力变化情况和温度变化情况大致相似，都呈现出波浪式上升的规律，且由于轴承固定端产热比游动端大，所以从图上可以看出三条曲线的峰值大小不一。

3 结论

(1)本论文应用有限元分析软件ANSYS对滚珠丝杠做了热瞬态分析，得到滚珠丝杠的温度场在不同时刻的分布，并通过间接热结构耦合的方法得到相对应时刻的应力场分布，了解到了滚珠丝杠的变形规律，对激光熔覆进给机构误差补偿具有一定的参考价值。

(2)激光加热和冷却速度很快，导致人们难以用实验的方法直接测量其瞬时温度分布。本论文在ANSYS中应用移动热源模拟实际过程中的摩擦热，使用环境温度函数加载的方法考虑外界环境的温升过程，激光热源和空气对流对滚珠丝杠的影响，对激光熔覆加工设备的误差分析提出了新的分析方法。

(3)在激光熔覆过程中由于工艺参数波动，导致熔覆的失效或者在某一位置处所形成的熔覆层的大小、形状发生畸形变化致使熔覆层质量的不稳定性无法控制，所以应通过补偿激光熔覆过程各工艺参数、提高加工设备本身的精度等方法来推动激光熔覆技术在国内实现产业化。

[1] 黄卫东. 激光立体成型[M].西安:西北工业大学出版社，2007.

[2] 章熙民，朱彤. 传热学[M].北京：中国建筑工业出版社，2014.

[3] Ganapathy V.Applied heat t ransfer[ M ] .Los Angeles :Pennw ell Pub , 1982 .

[4] 李维特,黄保海,毕仲波. 热应力理论分析及应用[M].北京：中国电力出版社，2004.

[5] 王宇，卢玲，李文韬.基于Ansys有限元网格划分方法应用研究[J].起重运输机械，2014(3):53-56.

[6] 李丽丽，李安玲，何强.ADGM高速电主轴热态特性仿真分析[J].组合机床与自动化加工技术，2014(8)：9-11.

[7] 冯瑞金，李蓓智，杨建国，等.基于MATLAB的高速磨削电主轴单元定子冷却管道的优化设计[J].机械设计与制造，2012(1):15-17,30.

[8]刘乐平,马元,钟名东. 高速高精数控车床进给系统热态特性研究[J].机床与液压，2012,40(3):36-39.

[9] 尹汉桥，尹明，张高平. 丝杠刚度受支撑方式影响的变化规律研究[J].机械研究与应用，2010(1)：45-46.

[10] 何龙，向存祥.滚珠丝杠副的有限元模态分析[J].成都航空职业技术学院学报，2015,31(2)：31-33.

[11] 赵万军. 基于ANSYS的滚珠丝杠进给系统静动态特性分析[J].机械传动，2010，34(5)：68-70.

(编辑 李秀敏)

Study on Thermal Characteristics of Ball Screw in Laser Cladding Feed System

LU Hua-wei ,LI Hu

(School of Mechanical Engineering and Automation,Northeastern University, Shenyang 110819, China)

The laser rapid prototyping develops rapidly, The study of feed system dynamic behavior contributes greatly to improve the surface quality of processed in the process of precision machining. In this paper, the ball screw of laser cladding feed system as the research object The friction heat in real process was simulated by a moved heat resource accompanied with the system in the software of ANSYS, and temperature rise of the external environment was taken into consideration. Within the influence of heat source and air convection mentioned above, the thermal-structural coupling analysis was did for the guide rail, and acquired the temperature field distribution and thermal deformation in different time.The result shows that the ball screw do similar changes in the machining process about the temperature and stress ,the law of the change is that the change of the temperature and stress present wave-like increasing tendency.

laser cladding; ball screw; finite element method(FEM);temperature filed; thermal deformation

1001-2265(2016)11-0057-03

10.13462/j.cnki.mmtamt.2016.11.016

2016-01-10

教育部项目种子基金(N130403007)；辽宁省科技项目(L2012076)

路华伟(1990—)，男，河南周口人，东北大学硕士研究生，研究方向为增材制造，(E-mail)luhuawei189@126.com。

TH164;TG659

A