苯酚与异丙醇烷基化合成异丙基苯酚的热力学和动力学

闫雪瑾，张 傑*，王文聪，李英霞

(1.北京化工大学化学工程学院，北京 100029； 2.北京师范大学燕化附属中学，北京 102500)



精细化工与催化

苯酚与异丙醇烷基化合成异丙基苯酚的热力学和动力学

闫雪瑾1，张 傑1*，王文聪2，李英霞1

(1.北京化工大学化学工程学院，北京 100029； 2.北京师范大学燕化附属中学，北京 102500)

基于Benson基团贡献法研究苯酚与异丙醇烷基化反应过程，确定了主、副反应的反应热、平衡常数及平衡转化率，得到反映热力学性质的反应方程式并建立反应的网络结构，为该体系的工艺设计提供热力学依据。在苯酚与异丙醇物质的量比为0.5～2.0、温度(513.15～573.15) K、空速8 h-1和催化剂颗粒(40～60)目[相当于粒径(0.45～0.30) mm]条件下进行本征动力学实验。选用幂数型动力学模型，对参数进行估值。用Runge-Kutta法进行数值积分，Simplex法对参数进行优化，F统计法对模型进行检验，最终得到能较好描述反应的本征动力学模型。

化学动力学；异丙基苯酚；烷基化；热力学；Benson基团贡献法；动力学模型

异丙基苯酚(IPP)是一种重要的精细化工原料及药物中间体，有邻、间、对3种异构体，可用作机器的清洁剂、黏合剂、染料、界面活性剂和防腐剂等。传统的生产工艺采用间歇釜式反应生产异丙基苯酚，工艺操作繁琐，易腐蚀，分离困难，耗能高，产量较低。为克服传统工艺的缺点，改善我国异丙基苯酚供不应求的状况，采用固定床积分反应器进行连续生产，并针对催化剂的不同种类进行研究[1-4]。罗明耀等[5]在温度(483～513) K，以酚铝盐为催化剂，对在鼓泡搅拌式压力釜内进行的苯酚和过量丙烯的烷基化反应进行动力学研究，由于丙烯过量，故假设丙烯的量为常数，该反应为多步连串且不可逆反应，从而建立了一组拟一级反应动力学模型。范建光[6]研究了苯与异丙醇气相烷基化合成异丙苯的热力学和本征动力学。本文对苯酚与异丙醇烷基化反应进行热力学和动力学研究。

1 烷基化反应热力学

质谱分析表明，苯酚(P)与异丙醇(IPA)烷基化反应的产物中有丙烯(Pr)、异丙基苯酚(IPP)、正丙基苯酚(NPP)、二异丙基苯酚(DIPP)和三异丙基苯酚(TIPP)，通过卡尔费休仪测得产物中有水(H2O)。据此推测体系中可能发生的化学反应，采用Benson基团贡献法从热力学角度对反应的可行性进行分析，主要分析各反应的反应热、平衡常数及平衡转化率，并建立网络结构，为工艺设计及催化剂研究提供热力学依据。

1.1 烷基化反应平衡常数及反应热

通过分析产物推测反应中可能发生的反应为：

主反应：

(1)

(2)

(3)

副反应：

(4)

(5)

(6)

(7)

(8)

由于反应在常压条件下进行，故理想气体恒压反应的平衡常数随温度变化，其关系可用范特霍夫(Van’t Hoff)方程表示[6]，见式(1-1)：

(1-1)

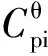
(1-2)

对平衡常数Kp在298.15 K与温度T间积分，可得平衡常数Kp与温度T的关系式，见式(1-3)：

(1-3)

(1-4)

(1-5)

部分组分恒压热容关联系数及热力学数据见表1。

表 1 部分组分的恒压热容关联系数及热力学数据[7]

其他组分IPP、NPP、DIPP和TIPP的热力学数据无法直接从相关文献中查到，因此，常用Benson基团贡献法估算未知组分的热力学数据，计算公式[8]为：

(1-6)

(1-7)

(1-8)

P、IPP、NPP、DIPP和TIPP的修正项及标准热力学的基团值[8]分别列于表2～3。

表 2 未知组分的修正项

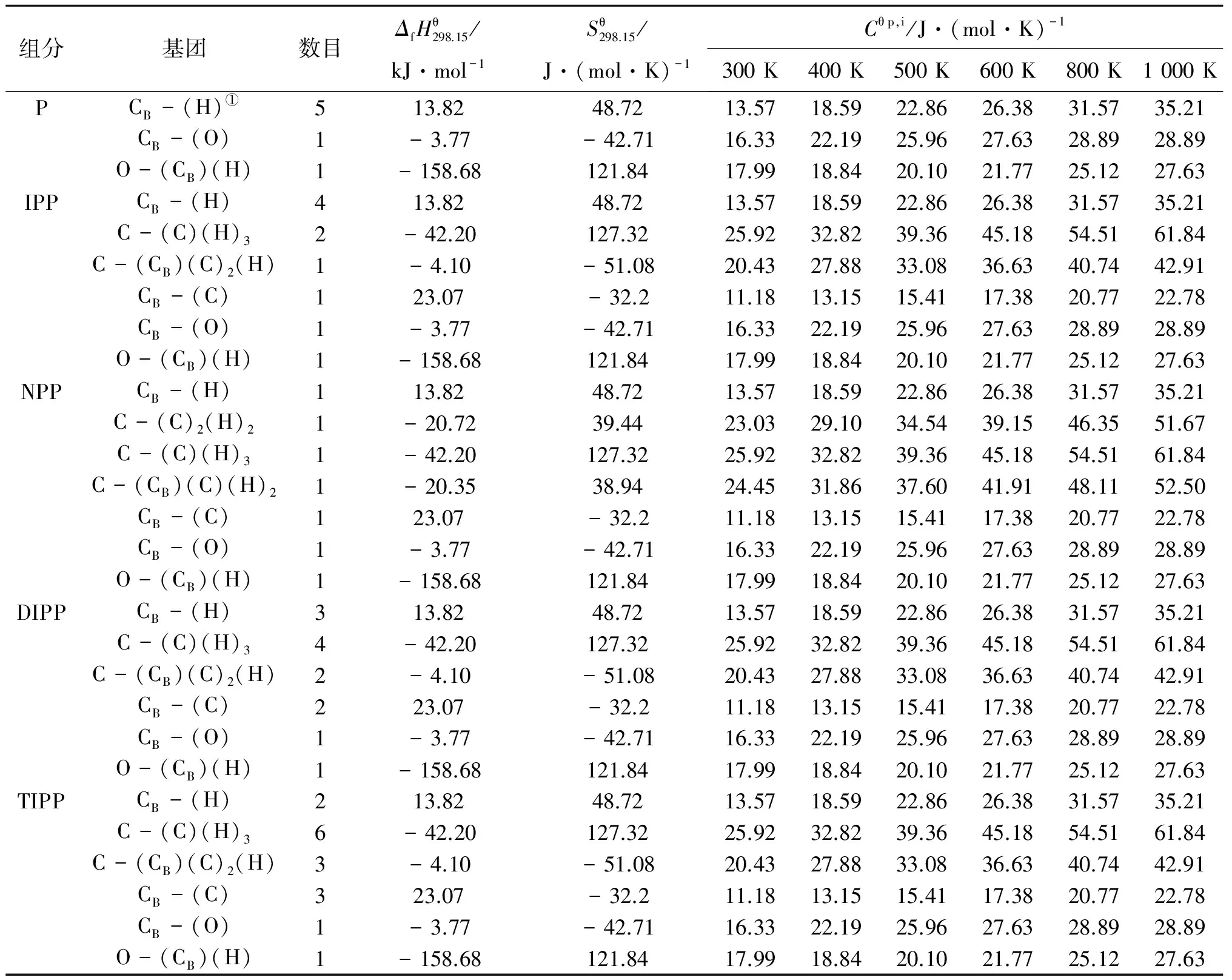
表 3 未知组分的标准热力学基团值

①CB为苯环中的碳原子

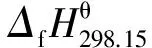
表 4 Benson法估算的未知组分的恒压热容关联系数及热力学数据

表 5 不同温度下各反应的平衡常数(Ky )

由表5可见，在(523.15～573.15) K，各反应的平衡常数均大于1，可认为反应(1)～(8)在热力学上为自发进行。

由公式(1-9)结合表1和表4数据得到反应(1)～(8)在(523.15～573.15) K的反应焓变，如表6所示。

(1-9)

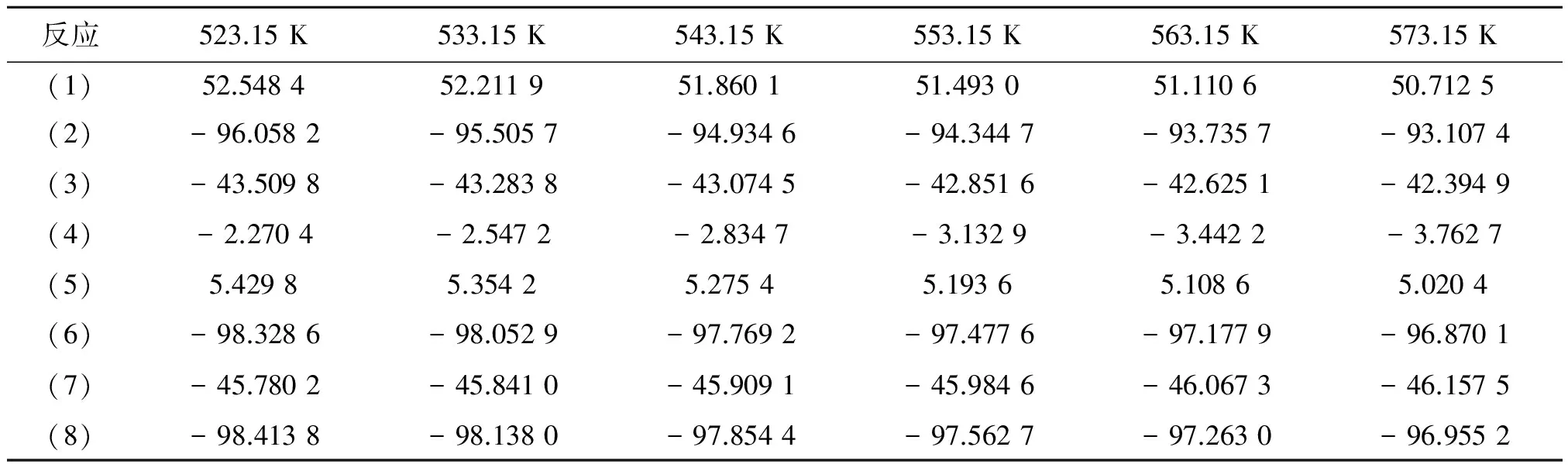
由表6可以看出，只有反应(1)和(5)为吸热反应，其他反应为放热反应，表明温度升高有利于IPA的水解，但不利于IPP的生成，并且各反应的焓变在(523.15～573.15) K变化很小，可认为是常数。

1.2 烷基化反应平衡转化率及网络结构

计算(523.15～573.15) K反应(1)～(8)的平衡转化率(X)，其中，对两种反应物进行的反应，以n(P)∶n(IPA)=1.25(由实验得最佳配比)进行计算。下面以反应(1)和(2)为例进行计算。

反应(1)：设IPA反应前的物质的量为a，则：

(1)

初始nB/mol a 0 0

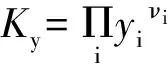
根据反应(1)计算出反应(4)和反应(5)关键组分(IPP)和(IPP)平衡转化率，3组反应数据见表7。

反应(2)：设Pr反应前的物质的量为b，P反应前物质的量为c，则：

(2)

初始nB/mol b c 0

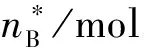
根据反应(2)计算方法，计算反应(3)、(6)、(7)和(8)的关键组分(IPA)、(Pr)、(IPA)、(Pr)的平衡转化率，结果见表7。

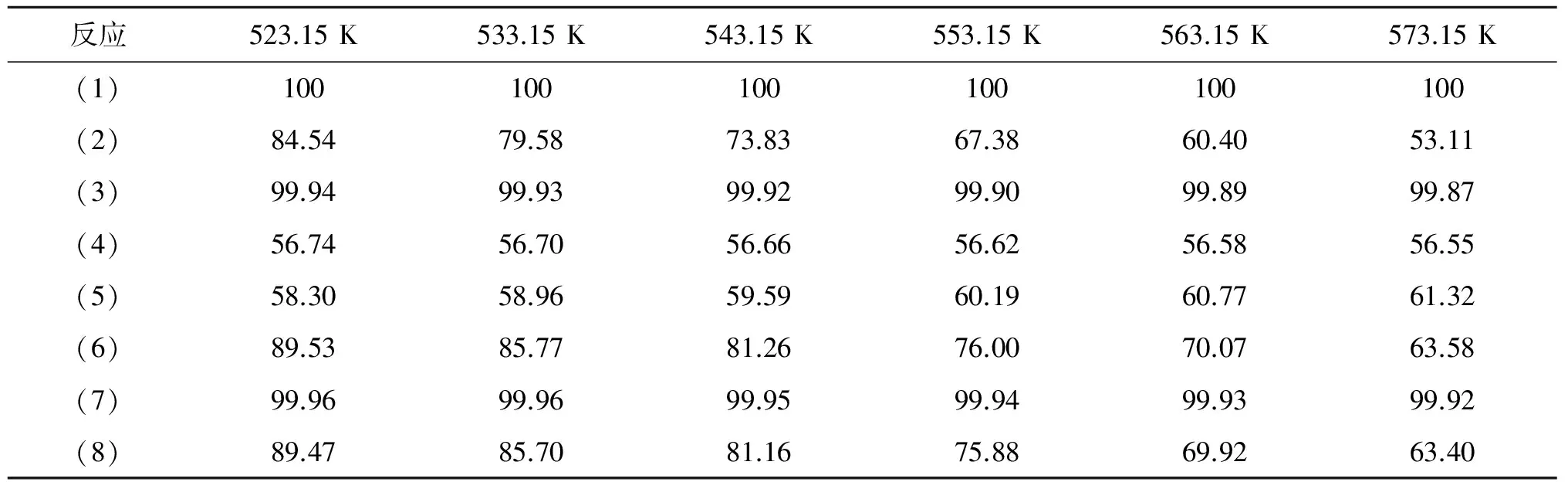
表 7 各反应关键组分不同温度下的平衡转化率(%)

由表7可以看出，反应(1)关键组分的平衡转化率为100%，为不可逆反应，其他反应均为可逆反应。产物中NPP和TIPP量极少，可忽略不计，可认为该反应体系中有两种反应物(IPA和P)和4种产物(Pr、H2O、IPP、DIPP)，结合计算的各步反应在不同温度条件下的平衡常数，得到以下6个反应方程式，并用热力学反应网络图表示，见图1。

主反应：

(1)

(2)

(3)

副反应：

(4)

(6)

(7)

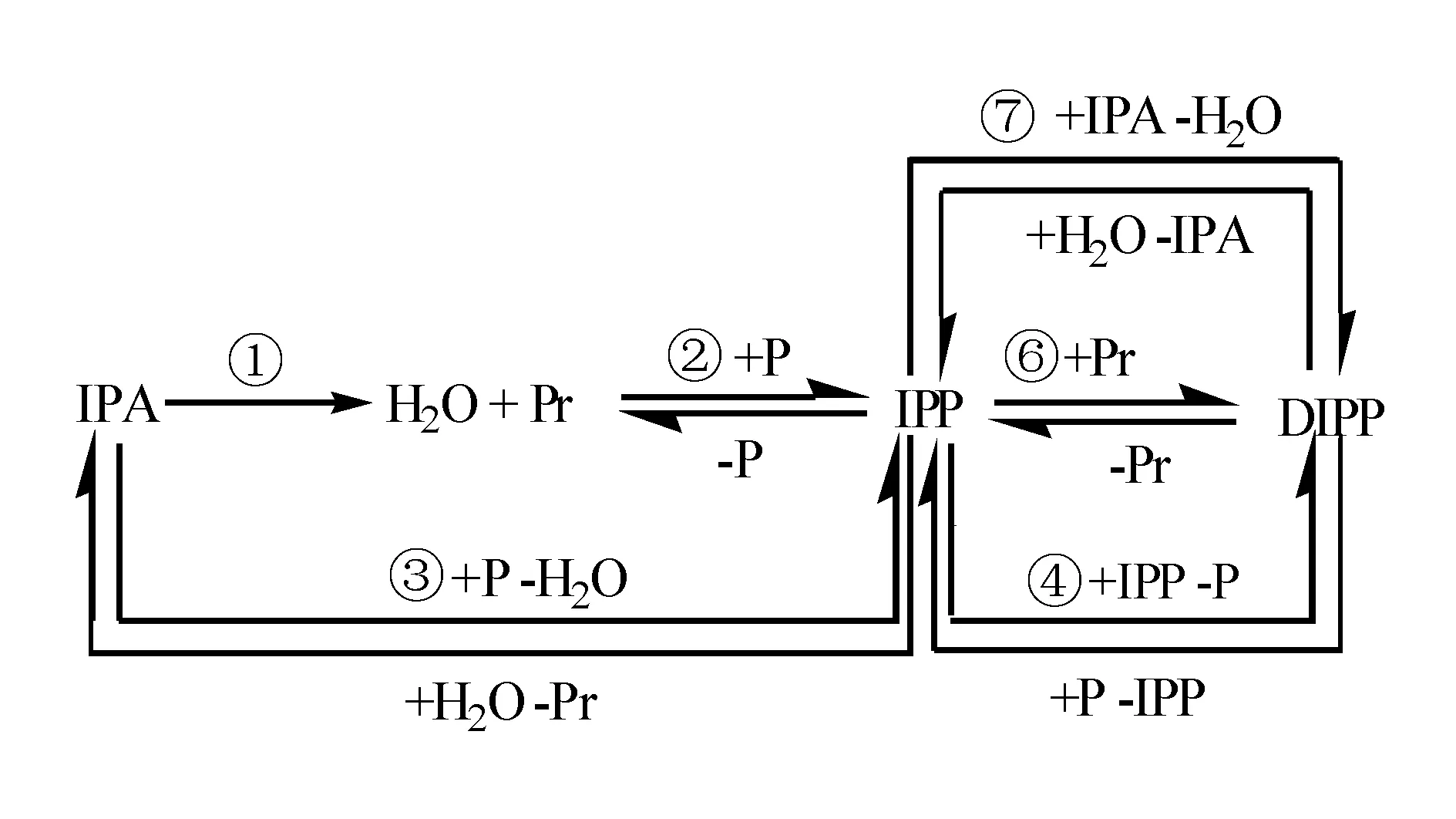
图 1 合成异丙基苯酚反应的网络Figure 1 Network of reactions of isopropylphenol synthesis

2 烷基化反应本征动力学

2.1 动力学实验条件的确定

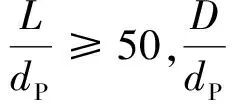
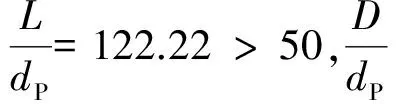
动力学实验首先要排除内扩散、外扩散的影响，根据文献[10]可知，当物料流速足够大时，可消除外扩散的影响，当催化剂颗粒粒径足够小时，可消除内扩散的影响。因此，通过增大线速度和改变催化剂的颗粒大小消除外扩散和内扩散的影响，结果如图2所示。

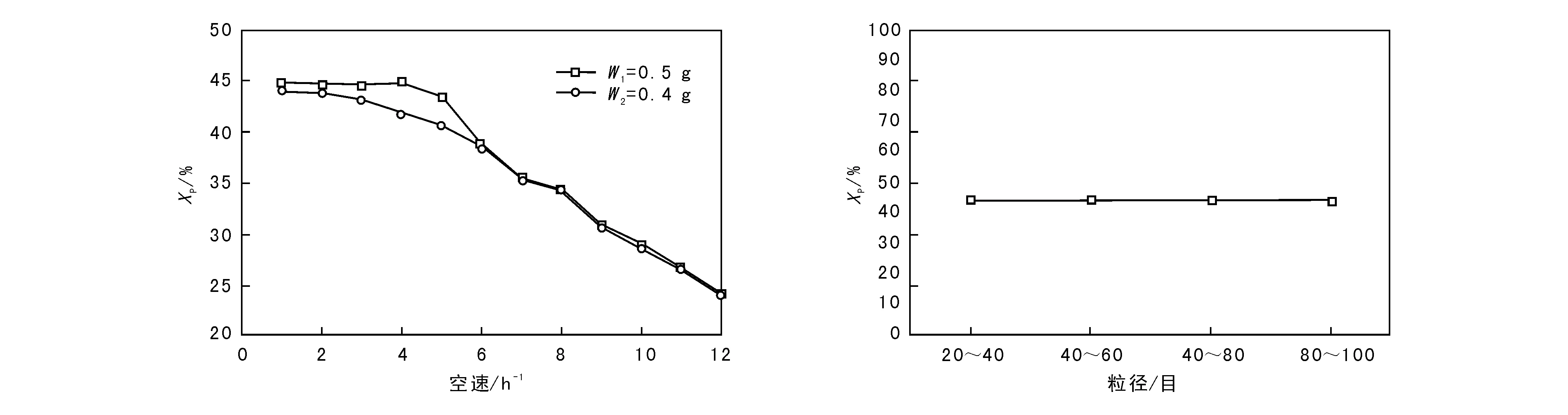
图 2 外扩散和内扩散实验结果Figure 2 External and internal diffusion test results of the catalyst

由图2可以看出，当空速为6 h-1和催化剂颗粒为(20～40)目时，可认为外扩散和内扩散影响已消除。

为保险起见，动力学实验选择在空速为8 h-1和催化剂颗粒为(40～60)目条件下进行，用于动力学实验的条件如表2所示。

表 8 本征动力学实验条件

2.2 动力学方程的建立

2.2.1 反应的确定及反应数据

由变空速实验可知，随着空速增大，P与IPA来不及发生烷基化反应，产物中也基本检测不到IPP和DIPP的存在，而此时由卡尔费休仪测得的H2O物质的量不变，且等于IPA的物质的量，表明产物中的H2O是由IPA分解得到，且该反应可瞬间完成，IPP和DIPP是由P和Pr连续反应得到。动力学实验得到的关键组分转化率小于热力学计算得到的平衡转化率，表明动力学实验各反应在未达到平衡前反应结束，可认为在动力学上发生的为不可逆反应，得到主反应(1)和(2)以及副反应(6)。

根据变空速实验得出反应(1)的速率远大于反应(2)和(6)，且IPA能在很短时间内100%转化，故假定IPA在反应器入口可瞬间转化，因此，体系为恒压变容反应，以反应(2)和反应(6)为速率控制步骤。

在动力学实验条件下进行实验，选取28组实验数据，并在反应器入口及出口对所有物质进行物料衡算，结果如表9所示。

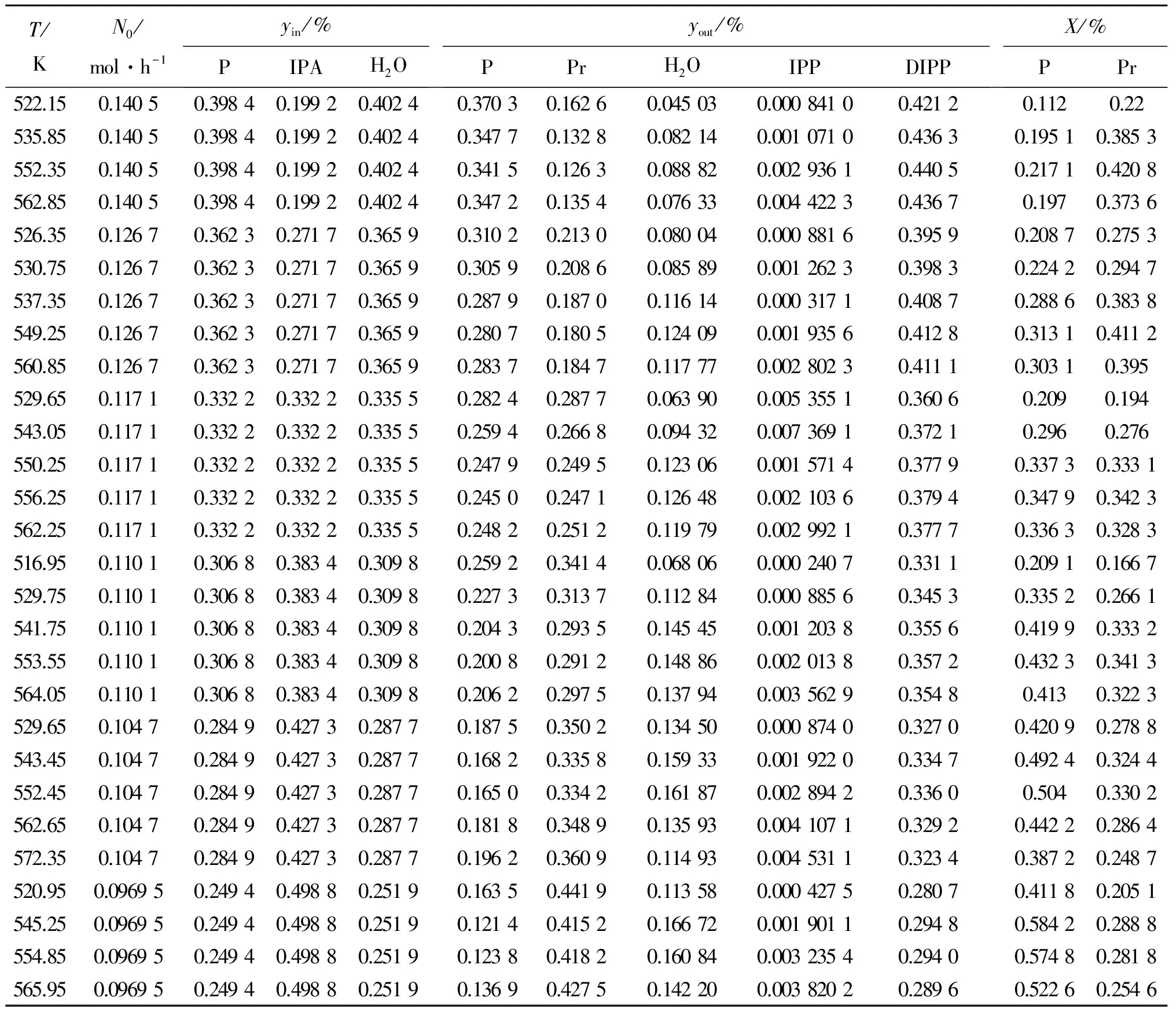
表 9 本征动力学实验数据

2.2.2 模型的建立

P与IPA的烷基化反应过程较为复杂，有很多副产物生成，前面已讨论某些副产物由于量很少，对动力学模型影响较小，故只考虑反应(2)和反应(6)。本文通过对在催化剂上进行烷基化反应动力学相关文献[6,11-13]的调研与对比，选出形式相对较简单、参数较少、对反应机理没有要求且与动力学实验数据能较好吻合的幂数型动力学模型。设两个反应的本征动力学速率方程为式(2-1)、(2-2)，其中，k02、k06、E2、E6、n1、n2、n3、n4为待估参数。

(2-1)

(2-2)

2.2.3 本征动力学模型参数估值的策略

本征动力学实验在活塞流条件下进行，并且消除了内、外扩散的影响，可按照理想反应器处理，即平推流反应器计算，因此，可用等温、等压下平推流反应器的模型方程[14](2-3)。

(2-3)

分别以P和Pr为关键组分，将r2、r6带入并整理得到：

(2-4)

(2-5)

对于反应(2)和(6)，方程(2-4)、(2-5)与反应器入口处“W=0时，XP=0，XPr=0”组成了一阶常微分方程，且初值为已知。可以通过本征动力学速率表达式(2-1)、(2-2)及参数初值(k02、k06、E2、E6、n1、n2、n3、n4)，采用一种数值算法沿着催化剂床层进行逐步积分，就可得到反应器出口P和Pr的转化率XP,out,C、XPr,out,C的计算值，将这两个值与实验测得的值XP,out,m、XPr,out,m进行比较，若其相对误差的平方和不能满足给定要求，则采用相应的优化方法[15]，根据误差信息，以适当步长和沿一定规律对模型参数初值进行调整后，循环上述步骤直到符合要求为止，此时的参数值即为最终动力学的参数值。

本文的参数估值优化方法为单纯形法(Simplex法)[16]，数值积分法选用定步长龙格-库塔法(Runge-Kutta法)[17]。参数估值过程所用的误差分析式为:

(2-6)

2.2.4 本征动力学模型参数估值结果

采用MATLAB软件进行编程，结合表8数据进行参数计算，并进行优化，得到P与Pr在ZSM-5分子筛上反应的动力学模型参数，结果见表10。

表 10 本征动力学模型参数

由此得到ZSM-5分子筛上P与Pr烷基化合成IPP的反应(2)和(6)的幂数型本征动力学方程为：

(2-1)

(2-2)

2.2.5 本征动力学模型结果检验

对本实验动力学模型的检验采用F统计法进行检验[18]，其统计量应大于一定置信度下由表查得的统计量的10倍，并且复相关指数应大于0.9。若模型不能满足以上要求，则模型无效[19]。

采用以下公式[20]进行检验，结果如表11所示。

复相关指数：

R2=1-S残/S总>0.9

(2-7)

统计检验：

(2-8)

总平方和：

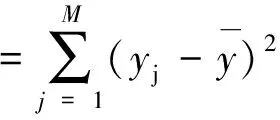
(2-9)

回归平方和：

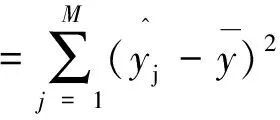
(2-10)

残差平方和：

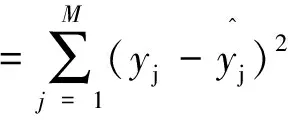
(2-11)

由表11可见，两个反应的本征动力学模型的复相关指数R2均大于0.9，模型的F值比置信度为99%和99.9%的临界F值的10倍大得多，符合本征动力学模型检验要求。

表 11 F统计检验结果

将XP和XPr的模型计算值与实验值对比，并绘成图3，再将二者的模型计算值与实验值的残差分布绘成图4。

由图3可以看出，所有的点均匀分布在对角线上及两侧，且两侧数据点均紧邻对角线，表明模型计算值与实验值吻合性良好。

由图4可以看出，XP和XPr的模型计算值与实验值的残差绝对值均在2%以内，残差总和接近于0，满足检验要求。结合表11，表明本征动力学模型(2-1)和(2-2)可信。

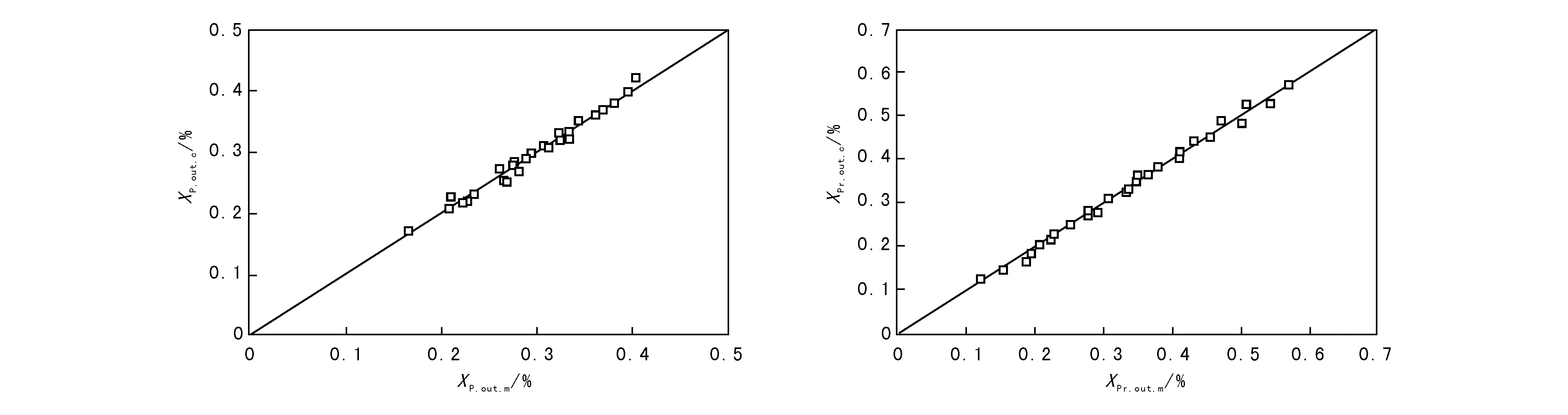
图 3 反应器出口处XP和XPr的模型计算值与实验值的比较Figure 3 Comparison of experimental and calculated data of model of XP and XPr at reactor outlet

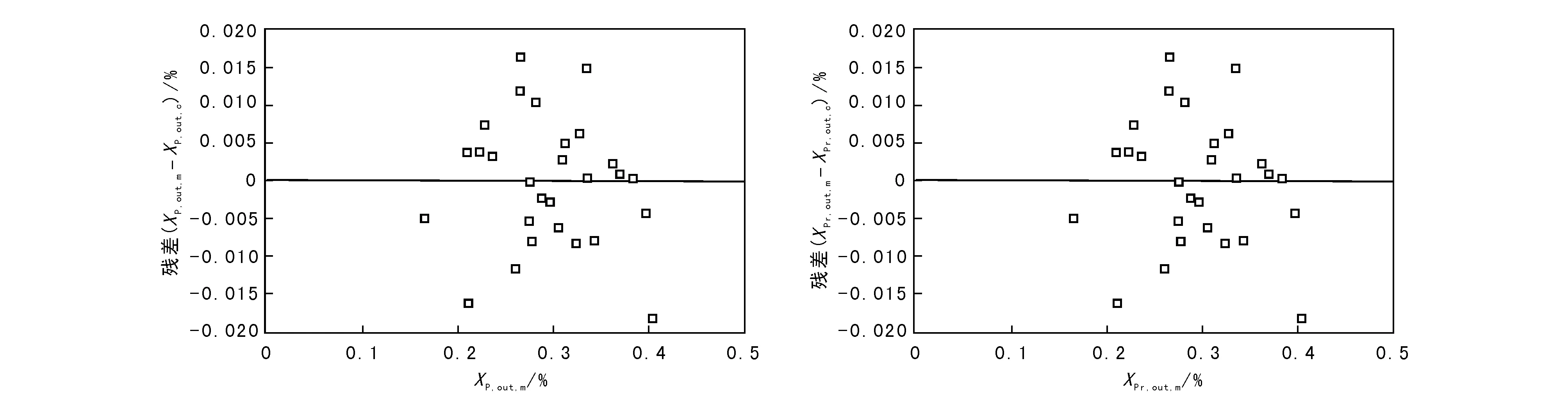
图 4 反应器出口处XP和XPr的残差分布Figure 4 Residual distribution of XP and XPr at reactor outlet

3 结 论

(1) 苯酚与异丙醇烷基化反应中只有反应(1)和(5)为吸热反应，其他反应为放热反应，表明温度升高有利于异丙醇的水解，但不利于异丙基苯酚的生成。由于所有反应的平衡常数均大于1，因此,各反应在(523.15～573.15) K均可自发进行。根据各反应的平衡转化率可知，只有反应(1)为不可逆反应，其他反应均为可逆反应，并得到反应的网络结构。

(2) 通过消除内、外扩散影响的实验研究，确定本征动力学的实验条件，经变空速实验及分析得到合成异丙基苯酚的主体反应为(1)、(2)、(6)。采用幂数型动力学模型经数值积分，参数估值与优化得到反应(2)和(6)的本征动力学方程及参数值。F统计法检验和残差分析表明，得到的动力学模型可信，在实验条件下能较好地描述反应过程。

符号说明:

A、B、C、D——关联系数;

c——浓度，mol·L-1;

dP——催化剂颗粒直径，mm;

Fw——原料体积流量，mL·h-1;

H——焓，kJ·mol-1;

k——反应速率常数，mol·(g-cat·h)-1;

L——催化剂床层高度，mm;

n——基团数目,物质的量，mol;

R——气体常数，8.314 J·(mol·K)-1;

S——熵，J·(mol·K)-1;

u——质量流速，g·h-1;

W——催化剂装填质量，g;

y——气体物质的量分数；

σ——对称数；

ν——反应计量系数；

Cp——定压摩尔热容，kJ·(mol·K)-1；

D——反应管内径，mm；

E——活化能，J·mol-1；

G——吉布斯自由能，kJ·mol-1；

K——化学平衡常数；

k0——指前因子，mol·(g-cat·h)-1；

N——物料摩尔流量，mol·h-1；

p——压力，MPa；

r——反应速率，mol·(g·h)-1；

T——热力学常数，K；

v——空速，h-1；

X——转化率，%；

Z——反应器轴向距离，mm；

η——光学异构体个数；

Δ——变化量；

下角标:

B——苯；

i——组分;

ext——外对称数;

int——内对称数;

in——反应器入口;

out——反应器出口;

r——反应;

f——生成;

c——计算;

m——测量;

上角标:

θ——标准态;

n——反应级数。

[1]李杨,魏立国,商永臣.HZSM-5分子筛上苯酚与异丙醇烷基化反应的研究[J].化学工程师,2010,24(173):18-21.Li Yang,Wei Liguo,Shang Yongchen.Alkylation of phenol with isopropanol over HZSM-5 zeolites[J].Chemical Engineer,2010,24(173):18-21.

[2]肖瑞杰.MCM-56分子筛及MCM-36分子筛催化苯酚与异丙醇烷基化反应的研究[D].哈尔滨:哈尔滨师范大学,2011.

Xiao Ruijie.Alkylation of phenol with isopropanol over MCM-56 and MCM-36 molecular sieve[D].Harbin:Harbin Normal University,2011.

[3]张丽.介孔材料的合成及其在苯酚与异丙醇烷基化中的催化性能[D].哈尔滨:哈尔滨师范大学,2013.Zhang Li.Preparation of mesoporous materials and their performance in alkylation of phenol with isopropanol[D].Harbin:Harbin Normal University,2013.

[4]王莹莹.复合分子筛催化苯酚异丙醇烷基化反应的研究[D].哈尔滨:哈尔滨师范大学,2014.

Wang Yingying.Research of alkylation of phenol with isopropanol over composite molecular sieve[D].Harbin:Harbin Normal University,2014.

[5]罗明耀,蔡守信.苯酚和丙烯烷基化反应动力学模型的研究[J].浙江工学院学报,1990,(3):46-53.

Luo Mingyao,Cai Shouxin.Study on kinetic model of alkylation reaction with phenol and propylene[J].Journal of Zhejiang Institute of Technology,1990,(3):46-53.

[6]范建光.YSBH-02催化剂上苯与异丙醇气相烷基化合成异丙苯的工艺条件及本征动力学研究[D].北京：北京化工大学,2004.Fan Jianguang.Operating conditions and intrinsic kinetics of cumene synthesis from gas-phase alkylation of benzene with isopropanol over a domestic YSBH-02 catalyst[D].Beijing:Beijing University of Chemical Technology,2004.

[7]金克新,赵传钧,马沛生.化工热力学[M].天津:天津大学出版社,1997:261-270.

[8]董新法,方利国,陈砺.物性估算原理及计算机计算[M].北京:化学工业出版社,2006.

[9]李绍芬.化学与催化反应工程[M].北京:化学工业出版社,1986:192-194.

[10]陈甘棠.化学反应工程[M].3版.北京:化学工业出版社,2007:121.

[11]李建伟,李成岳,蒋小川,等.C302铜基催化剂上甲醇合成的动力学研究Ⅰ.动力学模型[J].催化学报,2000,21(6):551-555.

Li Jianwei,Li Chengyue,Jiang Xiaochun,et al.Reaction kinetics of methanol synthesis over Cu-based catalyst C302Ⅰ.Kinetics models[J].Chinese Journal of Catalysis,2000,21(6):551-555.

[12]陈军辉.新型炭法烟气脱硫过程动力学研究[D].成都:四川大学,2004.

Chen Junhui.Kinetics research of new type carbon method flue gas desulfurization process[D].Chengdu:Sichuan University,2004.

[13]王振刚.Cu-Zn/Al2O3催化剂上醋酸间接加氢制乙醇本征动力学[D].北京：北京化工大学,2014.Wang Zhengang.Intrinsic kinetics for the indirect hydrogenation of acetic acid to ethanol on the Cu-Zn/Al2O3catalyst[D].Beijing:Beijing University of Chemical Technology,2014.

[14]贝伦斯M,霍夫曼H,林肯A,著.化学反应工程[M].2版.张继炎,徐建国,齐鸣斋,译.北京:中国石化出版社,1994.

[15]朱炳辰.化学反应工程[M].北京:化学工业出版社,1996:112-133.

[16]邓建中,葛仁杰,程正兴.计算方法[M].西安:西安交通大学出版社,2000:56-68.

[17]徐士良.FORTRAN常用算法程序集[M].北京:清华大学出版社,1992:98-118.

[18]汪荣鑫.数理统计[M].西安:西安交通大学出版社,1999:262-276.

[19]江体乾.化工数据处理[M].北京:化学工业出版社,1984:128-132.

[20]朱中南,戴迎春.化工数据处理与实验设计[M].北京:烃加工出版社,1989:86-87.

Thermodynamics and kinetics of alkylation of phenol with isopropanol to isopropylphenol

YanXuejin1,ZhangJie1*,WangWencong2,LiYingxia1

(1.College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, China;2.Yanhua Middle School Attached to Beijing Normal University, Beijing 102500, China)

The alkylation reaction of phenol and isopropanol was studied based on the Benson group contribution method,so as to confirm the reaction heat,equilibrium constants and equilibrium conversion rate of the main and side reactions.The reaction equation reflecting the thermodynamic properties and network structure for reaction were then established,providing thermodynamic evidence for process design of the system.The intrinsic kinetics experiments were carried out under the condition of space velocity 8 h-1,molar ratio of phenol to isopropanol 0.5-2.0,temperature (513.15-573.15) K,and catalyst particle size (40-60) mesh [corresponding to the particle size of (0.45-0.30) mm].The thermodynamic parameters were estimated by using exponential kinetic model.Runge-Kutta method was used to carry out numerical integration,Simplex method was used to optimize the parameters,and F statistics method was used to verify the model.Finally,a good description of the intrinsic reaction kinetics model was obtained.

chemical kinetics;isopropylphenol;alkylation;thermodynamics;Benson group contribution method;kinetic model

O643.31;O642.1 Document code: A Article ID: 1008-1143(2016)10-0064-10

2016-06-08;

2016-08-25 基金项目：国家自然科学基金(21206008)资助项目

闫雪瑾，1990年生，女，河北省保定市人，在读硕士研究生，研究方向为化学反应工程。

张 傑，副研究员，研究方向为多相催化与催化反应工程。

10.3969/j.issn.1008-1143.2016.10.012

O643.31;O642.1

A

1008-1143(2016)10-0064-10

doi:10.3969/j.issn.1008-1143.2016.10.012