基于 Vague 集的铁路车流径路优化

武 威，董宝田，陈光伟，张晓栋

（1.北京交通大学 交通运输学院，北京 100044；2.中国铁路信息技术中心, 北京 100844）

基于 Vague 集的铁路车流径路优化

武 威1，董宝田1，陈光伟2，张晓栋1

（1.北京交通大学 交通运输学院，北京 100044；2.中国铁路信息技术中心, 北京 100844）

为实现车流径路时间消耗与距离消耗的双重优化，求得更合理径路，针对以往径路优化模型没有考虑径路走行时间的问题，将车辆在车流径路上的运行时间分为在途时间与在站时间，并结合信息化手段对在站时间的历史数据进行统计分析来确定在站时间参数，建立以车辆在路网上运行的路径最短和时间最短为目标的多目标优化模型，采用 K 短路算法求出满足约束的合理径路集，并引入Vague 集来对合理径路集进行评价，从而得到满意解，最后通过算例验证了模型的有效性与算法的可行性。

铁路运输；K 短路算法；Vague 集；车流径路；铁路网

铁路车流径路问题是铁路运输的关键性问题，不少专家和学者都对此问题展开深入研究与探讨。宋建业[1]采用邻接矩阵存储的方法，并在基于支点站的全国铁路环状路网图上，利用 dijkstra算法求解最短径路，通过最短径路线来确定起终点站为非支点站的情况，在路网规模较小时可以有效解决最短径路的问题，但实际中随着路网规模的扩大，最短径路往往难以确定；施其洲等[2]针对路网上的双向空、重车流同时进行多目标线性规划，从整体的角度优化车流径路并尽可能提高线路能力利用率；靳来勇等[3]分析影响区域车流径路确定的因素并给出其制约因素和目标函数；李明博等[4]结合铁路现场的实际情况，提出合理非最短车流径路存在的原因，并对其进行理论解析，从宏观上对车流的分流流向进行分析。以上的车流径路研究均以车辆走行距离为主要考虑因素，但运输时间也是客户非常关心的问题，目前铁路货物运到时间难以准确预测，客户无法有效掌控运输时间，致使很多运输时间敏感型客户对选择铁路运输存有顾虑，对铁路在运输市场上的竞争产生不利影响。因此，考虑信息化手段，利用铁路大数据来估算车流径路上的时间消耗，对车流径路确定过程中的车辆走行时间消耗和距离消耗进行双目标优化，以求得满意的车流径路。

1车流径路的时间消耗

图1　车辆在车流径路上走行的时间消耗

（1）车辆在途时间。车辆在途时间是指车辆在铁路区间线路上的运行时间。

（2）车辆在站时间。车辆在站时间包括如下。①对于装车站，在站时间包括：等待取车时间、取车时间、集结作业时间、编组作业时间、出发作业时间。②对于编组站或区段站，在站时间包括：到达作业时间、解体作业时间、集结作业时间、编组作业时间、出发作业时间。③对于卸车站，在站时间包括：到达作业时间、解体作业时间、等待送车时间、送车时间。这些时间大多具有随机性，有的时间波动小，如到达作业时间和出发作业时间；有的时间波动比较大，如车辆集结时间；采用不同作业方式的编组站，其解体和编组作业时间也不同。这些情况均对车辆在站时间的估计造成很大困难。

（3）中转车平均停留时间。随着信息技术革新和铁路信息化的发展，信息化手段对监测列车运行位置和运行状态起到了关键作用。在实际运营组织过程中，车辆在装车站装车时会提报装车报文，挂运该车辆的列车在出发时会提报列车出发报文，列车到达编组站时会提报列车到达报文，车辆在卸车站卸车时也会提报卸车报文。在计算车辆在装车站的在站作业时间时，可以通过出发报文与装车报文的时间差确定；同理，计算车辆在编组站的车辆中转停留时间，也可以根据编组该车辆的列车在该站的列车到达报文和列车出发报文的时间差来确定。这样就可以得到车辆的在站时间消耗。因此，统计每个车辆在经由技术站的历史中转停留时间，采用求加权平均数的方法确定中转车平均停留时间，计算公式为

式中：∑ N有t有为有调中转车总停留车小时；∑ N无t无为无调中转车总停留车小时；∑ N有为有调中转车数；∑ N无为无调中转车数。

2车流径路的双目标优化模型构建

给定有向图 G = (V，E，l，t)，V 是顶点集，E是边集，l，t 是边上的权。给定车流径路为 f，xij定义为关于运行径路 f 上是否包含弧段 (i，j) 的 0-1 变量，当弧段 (i，j) 在 f 上，车辆由 i 运行到 j 时 xij= 1，否则 xij= 0。

构建优化模型如下。

式中：Z 为目标值；Z1为总车公里数；Z2为总走行时间；lij为 i 站与 j 站之间的站间里程；tij表示 i 站与 j 站之间的运行时间；θ1为 Z1相对于总目标值 Z的权重；θ2为 Z2相对于总目标值 Z 的权重；s，t 分别代表径路的起点和终点；xij为 0－1 变量，等于 0表示车辆运行径路不含弧段 (i，j)，等于 1 则表示径路经过弧段 (i，j)。

公式 ⑸ 表示节点守恒条件，对于径路的经由节点 i，其他节点指向节点 i 的有向线段与节点 i 发出的有向线段数目相等；公式 ⑹ 表示在满足公式⑸ 的条件下，对于任意一个节点 i，至多只能有 1条径路与其相邻节点相连；公式 ⑺ 表示目标值 Z1，Z2相对于总目标值 Z 权重之和为 1。

第一，教材内容要以市场需求为导向，内容结构设计上要将教材文字、电子课件、视频教材、音声等进行统一起来，从而建立起立体化的实训教材，帮助学生更直观、更准确地把握商务日语的使用方法；第二，编制校本教材。商务日语是一个实践性极强的复合型课程，各个高校可以结合本地区产业布局及开发状况，编写符合本地区实际情况的校本教材，并在使用过程中进行不断地改进和完善；第三，采取模块化、互动式、多案例的编写方法，逐步推进商务日语的跨文化交际技能，将实训教材设计与高校专业特色实训室建设相结合，为学生模拟一个与实际工作岗位相似的环境，帮助学生尽快融入到实训课程当中，并提高他们在商务场景中日语语言的应用能力。

为方便讨论，模型暂不考虑线路能力问题，只对给定 OD 的单一车流径路进行优化。在求解多目标优化模型时，各目标之间通常存在冲突，针对某个目标具有优势的解对于另一个目标来说可能并非最优，因而对于这个多目标最短路径问题，其结果往往不存在最优解，而只有满意解。

3基于Vague集的车流径路方案评价

Vague 集在 Fuzzy 集的基础上[5]引入了真隶属度 t 和假隶属度 f，将一元隶属度 t 扩展至二元的真隶属度 t 和假隶属度 f，将 Vague 集用区间的形式表示为 A = [t，1- f ]，其中真隶属度 t 表示支持，假隶属度 f 表示反对，并且还可以表示出中立的比例为 1- t - f。以投票模型为例，如果 Vague 集A = [0.5，0.7]，则表示赞成投票的比例为 0.5，不赞成的为 0.3，弃权比例为 0.2[6]。可见，与 Fuzzy 集相比，Vague 集对不确定性的描述具有更加丰富的信息和意义。

对于真隶属度 t 和假隶属度 f 的确定，常常采用 Vague 集指标公式。定量指标分为效益型和成本型 2 类，效益型指标值越大结果越优，而成本型指标值越小结果越优。据此特点结合 Vague 集可将指标值进行规范化处理。

对于成本型指标，规定真假隶属度分别采用下式计算[7]。

式中：v 为车流径路方案评价指值；vmax和 vmin分别为 v 该指标的理论最大值和最小值，一般是 v 的计算最大指标值和 v 的计算最小指标值乘以对应的最值系数。

对于效益型指标，规定真假隶属度分别采用下式计算[7]。

Vague 集的记分函数用来衡量备选方案满足决策者要求的程度，记分值越高，方案越优。根据Vague 集的相似度来构造记分函数，假设 2 个 Vague值为 X = [tx，1－ fx]，Y = [ty，1－ fy]，则它们之间的相似度定义为[8]

方案 Ai可以用 Vague 集表示为[9]

式中：C1，C2，…，Cn分别为从不同角度对方案 Ai的评价指标；tij表示方案 Ai对评价指标 Cj的真隶属度；fij表示方案 Ai对评价指标 Cj的假隶属度。

对方案 Ai的各评价指标的重要性赋权值，权重分别为 ω = {ω1，ω2，…，ωn}，其中 ω1，ω2，…，ωn∈ (0，1)，并且 ω1+ ω2+ … + ωn= 1。假设理想方案的所有 Vague 值均为 [1，1]，则备选方案与理想方案之间的相似度记分函数计算公式为[8]

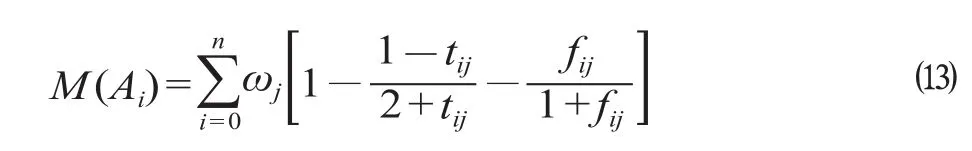
4实例分析

将铁路网中衔接3个及3个方向以上线路的车站作为支点，建立以支点站为节点的路网或局部路网简化拓扑结构，可以有效缩小问题规模，提高运算效率。以如图2所示的局部路网简化拓扑图为例，求解丰台西到徐州北的车流径路。路网拓扑结构图上只表示出支点站，边上的权值表示两站之间的距离。车站名与车站 ID 的对应情况如表1所示。

如果区段起始站和结束站属于同一铁路局的管辖范围，则查定对应铁路局的平均旅行速度统计值作为区段的平均旅行速度；如果区段的始发站和终到站分别属于不同铁路局，则求出两局平均旅行速度统计值的算术平均值作为区段的平均旅行速度。通过区段里程除以区间平均旅行速度可以计算其相应区段的运行时间。路段参数如表2所示。

图2　简化的局部铁路网结构

表1车站名与车站 ID

通过对图2中各站 30 d 的车辆到发报文进行分析，统计其平均有调作业时间和无调作业时间，将二者加权平均数作为车辆中转停留时间。各站的车辆中转停留时间如表3所示。

确定丰台西到徐州北的车流径路时，分别以距离和时间为权值，运用 K 短路算法计算前 K 条最短径路，结果分别如表4和表5 所示。

从表4和表5可以看出，车流径路一般不可能达到距离和时间同时最优，因而提取以上 2 种径路结果的交集，交集中的每一条径路代表一个可行方案，如表6所示。

由于方案中的指标属于值越小目标越优的成本型指标，采用公式 ⑻ 和 ⑼ 分别计算方案 A (i) 在指标 C1和 C2上的 Vague 集，定量指标 vmax为各备选方案中该指标的最大值乘以系数 1.2，vmin为各备选方案该指标的最小值乘以系数 0.8[7]，计算结果如表7所示。

表2　路段参数

表3　车辆中转停留时间

表4　以距离为权值的最短径路 　km

表5　以时间为权值的最短径路 　h

表6　满足时间和距离约束的径路交集

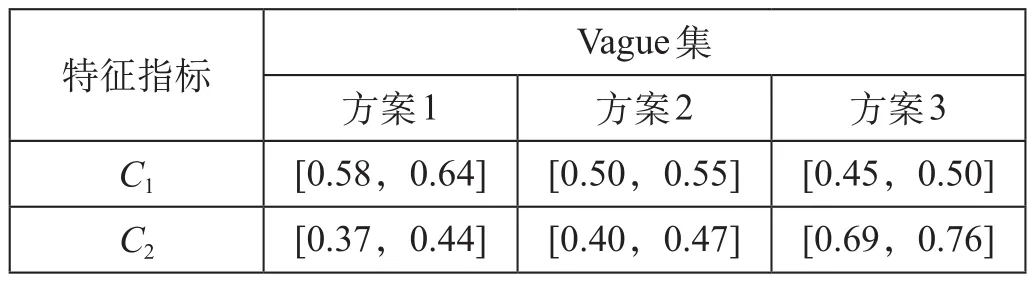
表7　不同方案对应不同指标的 Vague 值

由于需求不同，客户对运输距离 (成本) 和运输时间的预期也不同。令 ω1= 0.45，ω2= 0.55，根据 ⒀ 式，计算出 3 种方案的记分函数值为M (A1) = 0.46，M (A2) = 0.44，M (A3) = 0.58，则M (A3) ＞ M (A1) ＞ M (A2) 。

由表6可知，方案 1 满足距离最短，方案 3 满足时间最短，方案 2 是折中方案。而用 Vague 集求解距离与时间协同优化的结果是方案 3 优于方案1，方案 1 优于方案 2。这是由于在用计分函数求解时，采用的 Vague 集理想方案 [1，1] 代表同时满足距离最短和时间最短的径路，而这种理想方案在算例中并不存在，因而选择合理径路是在给定权重下选择使距离和时间尽可能小的径路。方案 1、方案 3 与理想方案的对比如表8所示。

在表8中，方案 2 相比理想方案的距离消耗为(806－775)/775 = 0.04，相比理想方案的时间消耗(39.79－33.38)/33.38 = 0.19，结合给定权重可以确定总的多余消耗为 0.04×0.45 + 0.19×0.55 = 0.12。其他方案的计算方法与此相同。加权消耗值表示相对于理想值的总增加消耗，总增加消耗越小越接近最优，即最满意方案为方案 3，其次为方案 1，再次为方案 2。

表8　各方案与理想方案的对比

5结束语

针对车流径路的优化问题，建立了以距离消耗最短和时间消耗最少的多目标优化模型，通过利用历史数据确定车辆在途、在站的时间消耗参数，并结合 K 短路算法求出合理径路集，运用 Vague 集的方法来分析合理径路集来确定满足约束的满意解。通过分析可知满意解符合实际情况，并为确定车流径路的时间消耗预测提供一种可行的方法，在一定程度上有助于货物运到时间的确定。下一步研究方向可以对相同 OD 的车辆在同一编组站的中转停留时间分货种、分方向进行细分，更加精细化地确定车辆中转停留时间，从而使车流径路的时间消耗值预测更加准确，使车流径路的确定更加优化。

[1] 宋建业. 全国铁路车流径路计算方法的研究[J]. 兰州铁道学院学报，1990，9 (3)：37-44.

SONG Jian-ye. The Research on the Calculation Method of the Wagon Routing on the Railway Network[J]. Journal of Lanzhou Railway College，1990，9 (3)：37-44.

[2] 施其洲，施 勇. 具有双向、空重车流的路网车流径路多目标线性规划模型及算例[J]. 铁道学报，1999，21(1)：1-9.

SHI Qi-zhou，SHI Yong. Multi-Objective Linear-Programming Model and Its Algorithm for Car Flow Routing with Bidirectional Heavy and Empty Cars in Railway Network[J]. Journal of the China Railway Society, 1999，21(1)：1-9.

[3] 靳来勇，叶玉玲，赵永旭，等. 区域性路网车流径路的选择[J]. 中国铁路，2005(12)：49-51.

JIN Lai-yong，YE Yu-ling，ZHAO Yong-xu，et al. Choosing of Regional Railway Network Car Flow Routing [J]. Chinese Railways，2005(12)：49-51.

[4] 李明博，季 令. 合理的非最短车流径路理论解析[J]. 铁道运输与经济，2008，30(6)：18-20.

LI Ming-bo，JI Ling. Theoretical Analysis of Reasonable Non-shortest Car Flow Routing[J]. Railway Transport and Economy，2008，30(6)：18-20.

[5] 江 伟. Vague 集理论及其在智能决策中的应用研究[D].南宁：广西大学，2008.

JIANG Wei. Application and Research of Vague Set Theory on Intelligent Decision[D]. Nanning：Guangxi University，2008.

[6] 符海东，卢正鼎. 基于 Vague 集距离的多评价指标模糊决策方法[J]. 华中科技大学学报(自然科学版)，2003，31(8)：77-79.

FU Hai-dong，LU Zheng-ding. Fuzzy Decision Making with Multicriteria based on Distance of Vague Set[J]. Journal Huazhong University of Science & Technology (Nature Science Edition)，2003，31(8)：77-79.

[7] 陈 琨，张翠东，孙家驷. 基于 Vague 集的互通式立交方案综合评价方法[J]. 公路交通技术，2008(4)：125-127.

CHEN Kun，ZHANG Cui-dong，SUN Jia-si. Synthetic Evaluation Method for Interchange Scheme based on Vague Set[J]. Technology of Highway and Transport，2008(4)：125-127.

[8] 李彦斌，张 恒，陈文姣. 基于 Vague 集的输电线路设计方案的优选[J]. 科技和产业，2011，11(11)：81-83.

LI Yan-bin，ZHANG Heng，CHEN Wen-jiao. Optional Option of Design Plans for Transmission Lines based on Vague Set[J]. Science Technology and Industry，2011，11(11)：81-83.

[9] 要瑞璞，沈惠璋. 基于 Vague 集投影及距离的模糊多指标决策[J]. 数学的实践与认识，2009，39(2)：19-22.

YAO Rui-pu，SHEN Hui-zhang. Fuzzy Multicriteria Decision Making based on Projectivity and Distance of Vague Sets[J]. Mathematics in Practice and Theory，2009，39(2)：19-22.

责任编辑：吴文娟

Optimization of Car Flow Routing based on Vague Sets

WU Wei1, DONG Bao-tian1, CHEN Guang-wei2, ZHANG Xiao-dong1

(1.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044，China；2.China Railway Information Technology Center, Beijing 100038，China)

Railway car flow routing optimization should take account of path distance as well as path realization time so as to mirror the real process of train operation. To overcome the shortage of lack of path realization time factor in previous optimization models, travelling time of freight car in car flow routing is divided into on-way time and on-station time, and IT technology methods are used to calculate on-station parameters based on historical data of on-station time so that a multiobjective optimization model is established with objectives of shortest path and shortest time; and reasonable path sets is obtained and estimated by Vague sets and algorithm of K-shortest path. Finally, the validity of the model and the feasibility of the algorithm are verified by computational example.

Railway Transportation; Algorithm of K-Shortest Path; Vague Sets; Car Flow Routing; Railway Network

1003-1421(2016)10-0042-06

U292.3

A

10.16668/j.cnki.issn.1003-1421.2016.10.09

2016-06-15

中国铁路总公司科技研究开发计划课题(2014X009-A)