考虑旅客行为的城际铁路分时段定价策略

杨书利

（北京铁路局 天津货运中心，天津 300142）

考虑旅客行为的城际铁路分时段定价策略

杨书利

（北京铁路局 天津货运中心，天津 300142）

目前，城际铁路采用统一定价方式，无法有效平衡客流分布，造成高峰时段超负荷运行，非高峰时段能力过剩的问题。分时段定价可以有效缓解高峰时段客流压力并提高非高峰时段的利用效率。为从实证角度验证分时段定价在平衡供求、疏导客流、提高效益等方面的优势，以弹性需求理论、分时段定价数学模型为基础，以沪宁城际铁路为研究样本，定量分析分时段定价的成本效益。研究结果表明，相比统一定价，分时段定价策略可以更有效地促进客流量的均衡分配并提高收益水平。

城际铁路；弹性需求；分时段定价策略；统一定价

票价是影响城际铁路客流量的重要因素。目前，城际铁路采用统一定价方式，无法有效平衡客流分布，造成高峰时段超负荷运行，非高峰时段能力过剩的问题，因而有必要结合城际铁路定价方法分析客流需求价格弹性和经济效益，研究分时段定价策略在客流调节中的作用，以缓解客流高峰时段运输组织压力。

1考虑旅客行为的城际铁路分时段定价方案

1.1客流需求价格弹性分析

客流需求价格弹性系数即客流需求对票价的弹性，指客流需求变化对票价变化的影响程度。

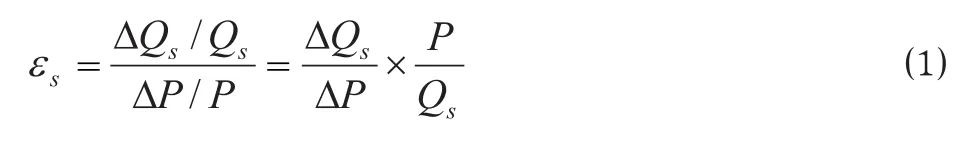
式中：εs为客流需求价格弹性系数；ΔQs为客流需求变动量；Qs为客流需求量；ΔP 为票价变动量；P 为票价。当 0＜| εs|＜1 时，说明客流需求缺乏弹性；当 1＜| εs|＜∞时，说明客流需求富有弹性；当 εs= 0 时，说明客流需求完全无弹性；当 | εs| = 1时，说明客流需求具有单位弹性。

与常规的固定需求下的轨道交通均衡配流模型相比，弹性需求下的均衡配流模型更符合实际情况[1]。根据客流需求价格弹性理论可以得知，城际铁路高峰时段客流需求价格弹性相对于非高峰时段小，因而应通过对客流需求价格弹性较低的高峰时段制订较高票价，限制客流剧增；对于客流需求弹性较高的非高峰时段降低票价，采用薄利多销策略诱导客流，增加总收益。

1.2分时段定价

以连接 2 个城市的城际铁路为研究对象，在 1 d的运营时间内，按时间顺序依次划分为时段，其中1 h 为一个时段，如全天运营时间为 7 : 00—21 : 00，则时段集合编号依次为 7 : 00—7 : 59 编号为1，8 : 00—8 : 59 编号为 2，以此类推。所有时段的集合记作 M，各时段发车数量和列车载客能力已知，并且各时段等间隔发车，各时段客流到达服从均匀分布。在此，假设其他交通方式运营对城际铁路票价没有影响，城际铁路票价仅受客流量的影响。由于不同时段不同票价下客流需求价格弹性不同，客流量有显著不同，因而根据客流需求价格弹性确定不同的票价，通过票价反求客流量。分时段定价过程[2]如图1所示。

图1　分时段定价过程

从图1可以看出，在考虑客流需求弹性条件下，所有时段统一票价，客流出现了明显的早晚高峰现象，缺乏可调控性；而分时段定价根据每个时段不同的客流量制订相应的票价，明显限制了早晚高峰客流迅猛增长，同时也促进了其他非高峰时段客流的增加。

2考虑旅客行为的分时段定价数学模型

2.1相关假设

城际铁路票价的优化受到很多因素的影响，在此只针对客流和票价的关系进行合理优化与改进，故作出以下假设。

（1）连接 2 个中心城市的城际铁路运营时中途不停站。

（2）城际铁路各个时段发车间隔固定，并且各时段内均匀发车。

（3）票价和客流量相互影响，客流需求随票价变化而发生弹性变化，票价和客流量不受其他自然因素和人为因素的影响。

（4）旅客到达客运站是随机的，并且每个时段内服从不同强度的均匀分布。

（5）各个时段的客流分布不均匀，有明显的早晚高峰现象。这是研究的前提条件，分时段定价根据客流不均匀性进行合理优化。

（6）城际铁路列车运营成本不受客流等其他因素影响。

2.2约束条件

（1）限价约束。城际铁路定价受到政府部门的限制与约束，通常政府部门会制订一个最高价和一个最低价，即

式中：k 为城际铁路时段编号；Pk表示 k 时段的票价；M 为城际铁路时段编号集合；Pmin和 Pmax分别表示政府部门限制的最低票价和最高票价。

（2）运输能力限制。由于城际铁路各时段发车数量与发车时间确定，假定各个时段列车的运输能力相同，每列车最大运输能力均为 q0，每个时段的运输量不能超过该时段所有列车最大运输能力之和，可以得到以下约束。

式中：qk为 k 时段的客流量；q0为每列列车最大运输能力；nk为 k 时段发车数量，nk= 60/tk，tk为 k 时段平均发车间隔。

2.3模型设计

考虑铁路部门盈利因素，满足时段客运能力约束，以铁路盈利最大化为上层目标，以均衡配流模型为下层目标，以不同时段的票价和客流量作为决策变量，争取达到各个时段客流分布均衡但不超饱和[3-4]。

2.3.1上层模型

按照铁路部门盈利最大化原则，以各个时段的票价 Pk作为决策变量，可以得到上层规划目标函数如下。

式中：F (Pk) 为 Pk票价下铁路部门的盈利水平；ck为 k 时段每位旅客平均运输成本；c0为每列车的固定成本。

2.3.2下层模型

考虑出行者成本费用，通过下层配流模型，力求达到各个时段出行者出行效用最低且相同，以各个时段的客流量作为决策变量，可以得到下层规划目标函数如下。

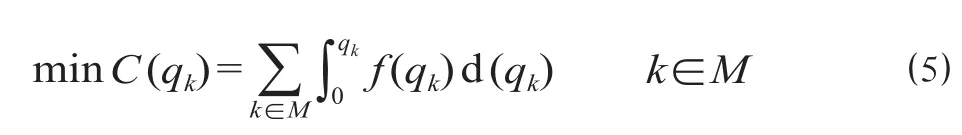
式中：C (qk) 为 k 时段 qk流量下的运输成本；f (qk) 为出行者各个时段成本效用函数。

城际铁路日客流量 Q 等于各个时段的客流量之和，即

城际铁路各个时段客流需求随票价发生弹性变化，因而在下层模型中考虑弹性需求，下层模型等价的优化模型为

2.3.3目标函数转化

由于弹性需求配流问题不能直接求解，必须要转化为固定需求问题，通过网络变换法虚拟一个时段，转化为固定需求问题。

假设 Qmax表示各个时段客流需求之和的最大值，最大客流需求与实际客流需求的差额用 qe表示，可得

故公式 ⑺ 右边部分可以等价表示为

由于 Qmax表示各个时段客流需求之和的最大值，故为定值，因而令 x = Qmax－y，公式 ⑺ 等价为

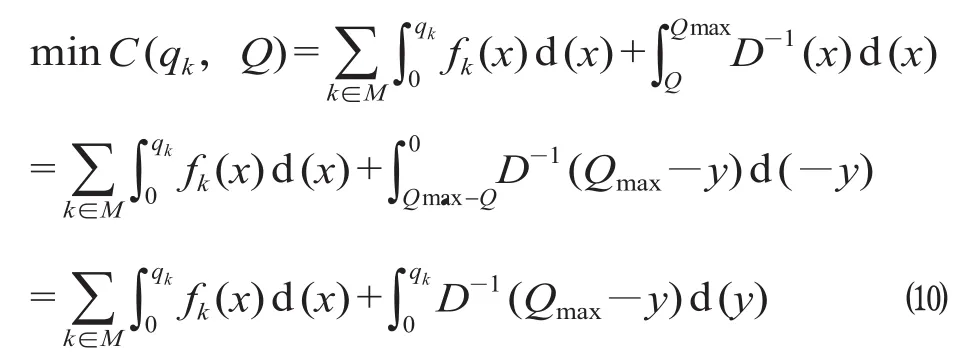
对客流需求反函数 D-1(Q) 扩展，该扩展函数是虚拟多余能力的函数，可以用 H (qe) 表示。

结合上式，公式 ⑽ 可以转化为

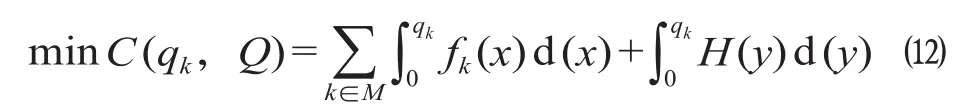
H (y) 可以看成是与各个时段成本函数一致的函数，故可以虚拟一个时段，该时段客流量大小就是多余能力值，因而此问题转化为了一个固定需求的问题。此时，运营的全部时段比原来的时段增加 1个，新时段集合记作为 M*，下层目标函数可以等价转化为

在函数求解过程中，主要采用遗传算法和Frank-Wolfe 算法相结合的方式，对上层数学规划模型利用遗传算法，对下层数学规划模型利用 Frank-Wolfe 算法求解，通过上层和下层反复迭代，最后得到的结果逐次逼近最优解[6-8]。

3案例分析

3.1基础数据

以沪宁城际铁路 (南京—上海) 为例，对其分时段定价策略进行研究。1 d 的运营时间可以按时间顺序划分为 16 个时段；根据 2013 年《铁道年鉴》和沪宁城际铁路调研资料，沪宁城际铁路不同时段客流基础数据如表1所示。

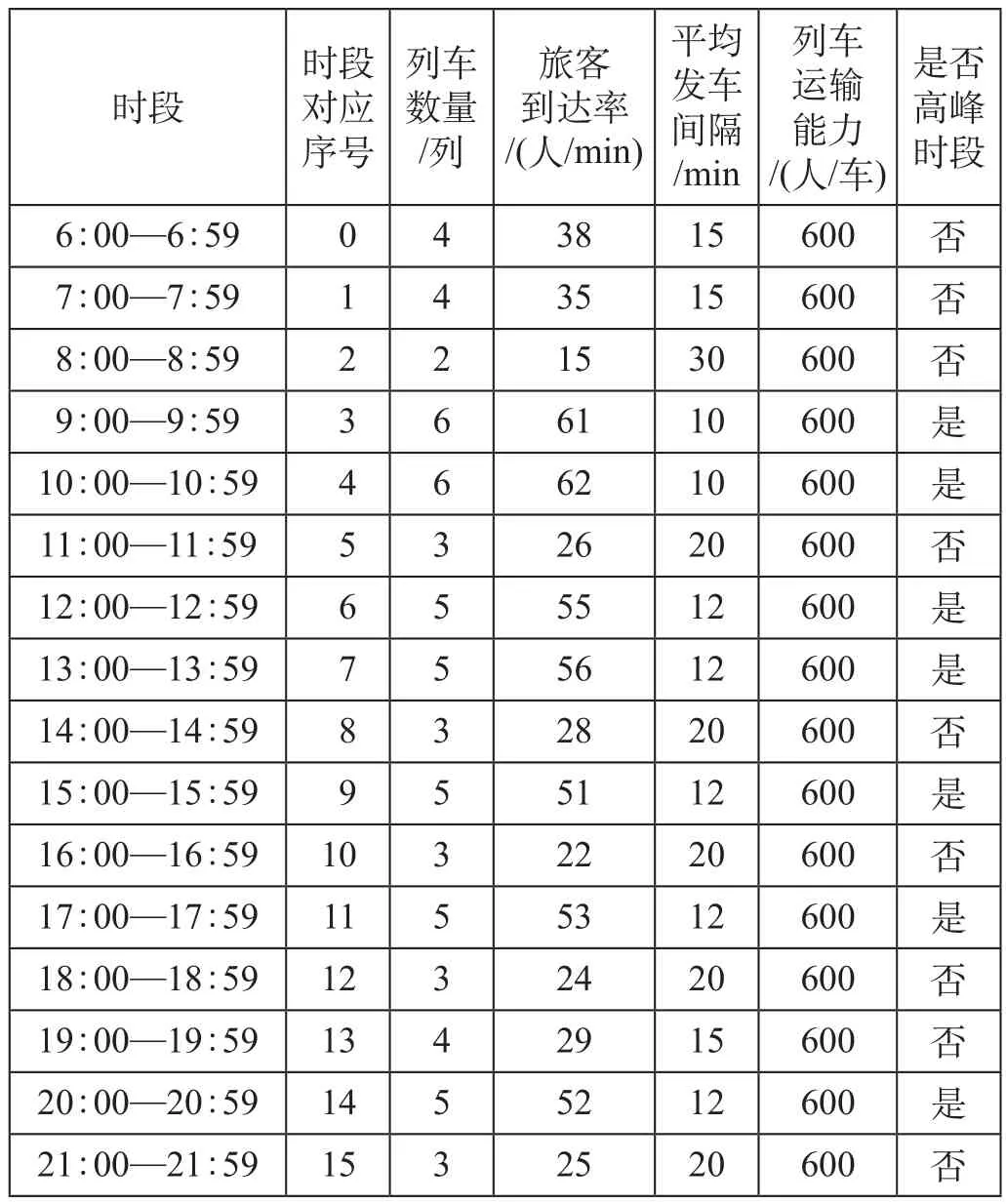
表1沪宁城际铁路不同时段客流基础数据

沪宁城际铁路全天的运输能力 Qmax= 39 600 人次；假设沪宁城际铁路最高限价 Pmax= 93.528 元，最低限价 Pmin= 37.056元；假定沪宁城际铁路运营可变成本 ck= 37.056 元，每列车固定成本 C0= 5 000元。

根据模型，可以计算得到各个时段的客流分布如表2所示。由表2可知，各个时段票价不同，16 个时段总客流量为 37 136 人次，比统一定价客流总量多 853人次。能力约束不同，客流量分布结果也各不相同，各个时段客流分配相对比较均衡，但都不超过已有的客运能力。

表2　分时段定价下各个时段的客流分布

3.2结果分析

3.2.1票价及效益分析

根据所提出的分时段定价法计算出的票价与现有的统一定价进行比较，可以得到沪宁城际铁路各时段的票价比较如图2所示。

从图2可以看出，分时段定价法计算得到的票价不同时段各不相同，与统一定价的票价相比有较大区别，票价较高的时段都出现在客流高峰时段。通过对高峰时段的高位定价，可以有效抑制客流的急速增长。从几个关键高峰时段 (如 4，5，7，8，10 等) 的数据可以看出，其所对应的客流量数据均有效控制在列车运输能力范围内，这说明分时段定价策略有效促进了客流量的均衡分配。从铁路部门效益方面进行分析，通过分时段计算收益，分时段定价方法下铁路总收益为 232.24 万元，统一定价下铁路总收益为220.96 万元，分时段定价方法总收益高于统一定价收益。

图2　沪宁城际铁路各时段票价比较

3.2.2客流结果分析

根据计算的客流结果，参考表2客流数据，沪宁城际铁路分时段定价与统一定价客流量比较如图3 所示。

图3　沪宁城际铁路分时段定价与统一定价客流量比较

由图3可知，分时段定价条件下高峰时段客流量依旧较大，但均未超过客运能力，舒适度和拥挤度相对较好；非高峰时段客流有较大的增长，各个时段客流分布结果较统一定价法更加合理。从旅客效用角度看，旅客虽然在高峰时段支付了较高费用，但在舒适度、避免拥挤和时效性方面体验更好，旅客可以根据自身偏好选择效用最大化的出行方案。

综上所述，沪宁城际铁路采用统一定价法时，票价完全稳定，但各个时段的客流分布不尽合理，高峰时段过度拥挤，超过运输能力限制，而非高峰时段客流较少，浪费运输资源。分时段定价方法下不同时段票价各不相同，但各个时段的客流量都能满足能力约束，没有出现过饱和状态。

3.2.3平均实载率分析

根据相关数据，利用公式 (实载率=列车实际承载人数/标定承载人数)，可以得到沪宁城际铁路各时段实载率。沪宁城际铁路分时段定价和统一定价各时段实载率比较如图4所示。

图4　沪宁城际铁路分时段定价和统一定价各时段实载率比较

由图4 可知，统一定价方法下各时段实载率波动较大，分时段定价法下各时段实载率趋近于1，说明分时段定价法更有利于沪宁城际铁路供给与需求合理匹配，更加满足列车开行方案要求。

4结束语

结合旅客行为分析城际铁路客流需求，构建不同时段旅客出行成本效用函数，建立分时段定价数学模型，以城际铁路部门收益最大化为上层目标函数，以出行者出行效用最低为下层模型，以各时段运输能力和铁路限价为约束条件，从而得到城际铁路分时段票价和分时段客流量分布，并以沪宁城际铁路为例进行分析。结果表明，分时段定价相比于统一定价而言，城际铁路一天中各个时段客流分布较为均衡，没有出现需求和供给不匹配的现象，并且铁路效益更佳。

[1] 孔繁钰，李献忠. 弹性需求下的轨道交通客流分配模型和算法研究[J]. 西部交通科技，2008(1)：83-87.

KONG Fan-yu，LI Xian-zhong. A Study on Passenger FlowDistribution Model and Algorithm for Rail Transit under Elastic Demand[J]. Western China Communications Science & Technology，2008 (1)：83-87.

[2] 史若燃，李志纯. 不同市场机制下多种交通方式定价模型研究[J]. 交通运输系统工程与信息，2010，10(5)：91-97.

SHI Ruo-ran，LI Zhi-chun. Pricing of Multimodal Transportation Networks under Different Market Regimes[J]. Journal of Transportation Systems Engineering and Information Technology，2010，10(5)：91-97.

[3] 曹国红，程 谦. 基于差别定价的铁路旅客票价优化研究[J]. 铁道运输与经济，2013，35(7)：6-10，23.

CAO Guo-hong，CHENG Qian. Study on Optimization of Railway Passenger Ticket Price based on Differential Pricing[J]. Railway Transport and Economy，2013，35(7)：6-10，23.

[4] 李志纯，谷 强，史 峰. 弹性需求下拥挤道路收费的模型与算法研究[J]. 交通运输工程学报，2001，1(3)：81-85.

LI Zhi-chun，GU Qiang，SHI Feng. Toll Model and Algorithm of Road Jammed with Traffic based on Elastic Demand[J]. Journal of Traffic and Transportation Engineering，2001，1(3)：81-85.

[5] 郭 啸. 弹性需求下道路收费的平衡配流模型的研究分析[D]. 长沙：中南大学，2007.

[6] 白 翰，刘浩学，倪怀州，等. 基于遗传算法的公交票价分级策略研究[J]. 交通运输系统工程与信息，2012，12(1)：180-184.

BAI Han，LIU Hao-xue，NI Huai-zhou，et al. Bus Fare Classification with Genetic Algorithm[J]. Journal of Traffic and Transportation Engineering，2012，12(1)：180-184.

[7] 杜 纲，钟石泉. 基于均衡原理的定位：运输路线安排问题模型及求解算法[J]. 系统管理学报，2009，18(4)：469-474.

DU Gang，ZHONG Shi-quan. Model and Algorithm for Location Routing Problem based on Equilibrium Principle[J]. Journal of Systems & Management，2009，18(4)：469-474.

[8] 郑鹏杰. 弹性需求条件下城际铁路时段定价问题研究[D]. 兰州：兰州交通大学，2015.

责任编辑：金 颖

Time-Segment Pricing Strategy of Inter-City Railway based on Passenger Behavior

YANG Shu-li

(Tianjin Freight Transportation Center, Beijing Railway Administration, Tianjin 300142，China)

Nowadays, uniformed pricing method of inter-city railway fails to effectively balance the distribution of passengers flow, and causes overburden operation during peak period and surplus capacity during non-peak period. by distinguishing prices based on different periods, the pressure on peak period can be eased and the efficiency of non-peak period can be improved. The paper verifies the advantage of time-segment pricing in the perspectives of balance between supply and demand, guidance of passenger flow, and elevation of operation performance by adopting elastic demand theory and time-segment pricing model, and takes Shanghai-Nanjing inter-city railway as an example by adopting quantitative method to analyze the cost and benefit of time-segment pricing. The result indicates that time-segment pricing strategy can effectively promote the balance of equilibrium distribution of passenger flow and increase the profit.

Inter-City Railway; Elastic Demand; Time-Segment Pricing; Uniformed Price

1003-1421(2016)10-0032-06

F532.5

B

10.16668/j.cnki.issn.1003-1421.2016.10.07

2016-08-18