基于张量秩校正的图像恢复方法

白敏茹,黄孝龙,顾广泽,赵雪莹

(湖南大学 数学与计量经济学院,湖南 长沙 410082)



基于张量秩校正的图像恢复方法

白敏茹*,黄孝龙,顾广泽,赵雪莹

(湖南大学 数学与计量经济学院,湖南 长沙 410082)

针对医学图像和视频图像的恢复问题，基于张量表示，研究有限样本下的低秩张量数据恢复问题，在张量奇异值分解(t-SVD)理论的基础上，提出了张量秩校正模型和两阶段张量秩校正方法，第一阶段是用张量核范数最小化模型求得预估解，第二阶段，根据预估解，求解张量秩校正模型，获得更高精度的解.构建了求解张量秩校正模型和张量核范数最小化模型的张量近似点算法，使得可以在实数域上对张量直接进行计算，并且从理论上证明了该算法的收敛性.通过对医学图像和视频图像的数值仿真实验，验证了本文所提出模型和方法的有效性，实验结果显示，张量秩校正模型和方法能够取得更高的恢复精度.

图像恢复；张量奇异值分解；张量秩校正；张量近似点算法

随着电子技术和成像技术的发展，从医学图像到遥感图像，从导弹精确制导，到人脸识别及指纹识别再到具有视觉功能的智能机器人，人类活动的方方面面都会产生或涉及到大量的高维图像.高维图像已经成为一种重要的多媒体形式，广泛存在于人们的日常生活中.图像在形成，传输和记录的过程中受多种因素的影响，图像的质量会有所下降，典型表现为色彩模糊和有噪声干扰等.这一降质的过程被称为图像的退化.图像恢复的目的就是尽可能地恢复退化了的高维图像的本来面目.

传统的图像处理方法是基于向量和矩阵的表示形式，往往破坏了这些数据的原始空间结构，在分析过程中不能够很好地刻画这些数据的本质和充分挖掘其内部特性.张量作为向量和矩阵表示的高阶推广，能够更好地表达高阶数据复杂的本质结构，已被广泛应用于计算机视觉与图像、人脸识别、医学图像和统计信号处理等研究领域中[1-6].

高维图像数据往往具有低维属性，张量完备化问题就是利用张量数据的低秩结构，是一种在有限样本或测量数据下最小化张量的秩的优化问题.最小化张量的秩是NP难问题，通常的处理方法有：1)将张量转化成矩阵，然后求解矩阵完备化问题[7]；2)用特殊的张量分解方法来分解张量，如CANDECOMP/PARA-FAC(CP)分解，Tucker分解等方法.

由于矩阵的核范数是矩阵秩的紧的凸逼近，因此对矩阵完备化问题的求解一般是将其转化为矩阵核范数最小化问题求解.对矩阵核范数最小化问题的求解有近似点算法(PPA)[8]，交替方向方法(ADM)，加速近似梯度方法(APG)[9].虽然低秩矩阵完备化问题得到很好发展，但张量完备化问题研究还很不完善.不同于矩阵秩只有一种定义，张量秩有多种定义.传统上主要有两种张量秩的定义，CP秩和Tucker秩，它们分别是基于CP分解和 Tucker分解的.将张量展开成矩阵，利用展开矩阵性质近似逼近张量的秩，是常用的处理方法.例如：Gandy[2]等用各片分别展开矩阵的核范数的和作为张量秩的近似逼近；Liu[5]等进一步将各片分别展开矩阵的核范数通过加权来近似张量的秩，并提出了HaLTRC算法求解该松弛模型(TSN).然而这两种逼近方法并不是张量秩函数的最紧的凸逼近[7].

Kilmer等[10]基于快速傅里叶变换可以将块循环矩阵对角化的思想，提出了张量奇异值分解(T-SVD)方法，使得张量可以在傅里叶变换下实现快速分解.基于T-SVD, Semerci等[6]提出张量核范数概念，对于3阶张量，利用张量核范数近似逼近张量的秩，建立了张量核范数最小化模型(TNN)，构建了交替方向方法(ADMM)求解该模型，并应用于多线性数据的图像压缩和恢复，通过对比，TNN逼近比TSN逼近效果更好.但是该文没有给出ADMM方法的收敛性结果，文中的ADMM算法一部分在实数域上计算，一部分在复数域上计算.与以往模型不一样，TNN模型的目标变量是定义在复数域即傅里叶域内的矩阵，约束变量是定义在实数域的.因此，根据这个问题的特点，设计更加有效的具有收敛性的优化算法，是亟需解决的一个问题.另外，文献[11]指出，矩阵核范数在某些情况下不是矩阵秩的最紧凸逼近，如对角元素被高度样本化，则矩阵核范数最小化模型求解低秩恢复问题的能力就会高度弱化，而矩阵核范数是张量核范数(TNN)的二阶形式.本文针对以上两个问题开展研究，主要贡献有两个：一是提出了张量秩校正模型(CRTNN)和两阶段张量秩校正方法，二是构建了张量近似点算法，用于求解CRTNN模型和TNN模型，从理论上证明了该算法的收敛性.仿真实验验证了本文所提出模型和方法的有效性．结果显示，在医学图像以及视频图像的恢复问题中，张量秩校正方法能够取得更高的恢复精度.

1 张量基本概念

张量即为多维数组，其元素所在位置需要3个或3个以上的变量来表示，可以记为A=an1n2…nN，其中A∈Rn1×n2×…×nN，这里ni，i=1,2, …,nN，称为维数，N为阶数.特别地，向量为一维张量，矩阵为二维张量.张量A的片是只有两个指标没有固定的矩阵形式，例如3阶张量A∈Rn1×n2×n3的前片表示为A(:,:,i)，i=1,2,3.针对彩色图像的数据结构，本文主要讨论3阶张量.本节简要介绍与张量奇异值分解有关的基本知识，更多详细的介绍见文献[10].

首先介绍由张量的前片构成的块循环矩阵，对张量A∈Rn1×n2×n3，其前片为n1×n2的矩阵A1,A2,A3其中Ai=A(:,:,i)，则有：

(1)

而快速傅里叶变换(FFT)可以将块循环矩阵转化成块对角矩阵，有如下形式：

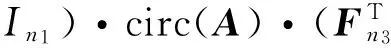
(2)

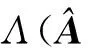
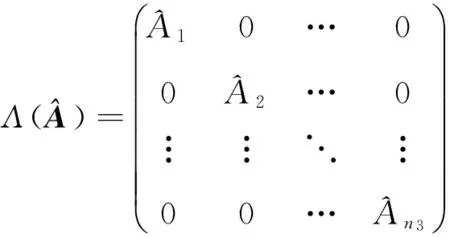
(3)

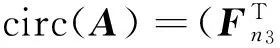
(4)

取MatVec变换作用于张量A∈Rn1×n2×n3的每一个前片，则MatVec(A)将张量A∈Rn1×n2×n3作用成n1n3×n2的矩阵：

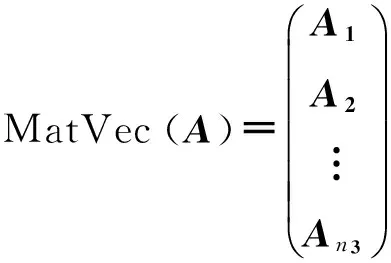
(5)

将MatVec(A)返回张量则用fold变换：

fold(MatVec(A))=A.

(6)

定义1.1[10]张量A∈Rn1×n2×n3和B∈Rn2×l×n3，则A与B的张量积定义如下：

C:=A*B=fold(circ(A)·MatVec(B)).

(7)

其中C∈Rn2×l×n3.

接下来介绍单位张量，张量的转置，张量奇异值分解(t-SVD).

定义1.2[10]张量In×n×l∈Rn×n×l为单位张量当它的第一个前片为n×n的单位矩阵，剩余两前片的元素均为0.

定义1.3[10]张量A∈Rn1×n2×n3，则张量A的张量转置AT∈Rn2×n1×n3，是通过保持第1个前片位置不变，第2个前片和第3个前片位置互换，并且分别对张量A每一个前片做转置得来.

定义1.4[10]张量A∈Rn×n×l为f-对角化张量当且仅当其每一个前片矩阵均为对角矩阵.

定义1.5[10]张量A∈Rn×n×l为正交张量当且仅当它满足：

AT*A=A*AT=In×n×l.

(8)

定理 1.6[10](张量奇异值分解(t-SVD))张量A∈Rn1×n2×n3，则A可以分解为：

A=U*S*VT.

(9)

其中U和V为正交张量，其中U∈Rn1×n1×n3，V∈Rn2×n2×n3，S∈Rn1×n2×n3为f-对角化张量.

最后介绍三阶张量的多线性秩和张量核范数(TNN)以及它们之间的联系.

在一定条件下，矩阵核范数是矩阵的秩的凸松弛，同理，张量核范数(TNN)是张量多线性秩的凸松弛[13].

2 张量完备化的秩校正方法

在图像采集过程中，由于各种原因，可能会出现图像数据损失的情况，即图像序列组成的张量X中有部分元素的值缺失.张量数据恢复问题即为张量完备化问题，就是利用张量数据的低秩结构，在有限样本或测量数据下最小化张量的秩的优化问题.Liu[5]等将张量按照不同方向分别展开成矩阵的核范数通过加权来近似张量的秩，建立了张量完备化的如下凸松弛模型(TSN)：

(10)

其中X(i)是张量X 的i模矩阵，并提出了HaLTRC算法求解该TSN模型.

Semerci等[6]则基于张量核范数TNN，提出了张量核范数最小化模型(TNN)：

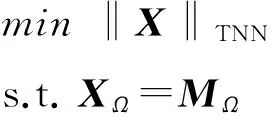
(11)

这里张量X,M∈Rn1×n2×n3，M在集合Ω里的元素是给定的，不在Ω里的元素则是0，即：

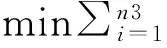
(12)

注意到矩阵核范数在某些情况下不是矩阵秩的最佳凸逼近，如对角元素被高度样本化，则矩阵核范数最小化模型求解低秩恢复问题的能力会高度弱化[11].为了获得更高精度解，针对张量核范数最小化模型(TNN)，本文提出了一个张量秩校正模型(CRTNN)：

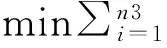
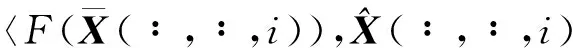
s.t.XΩ=MΩ.

(13)

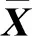
案例3：女，59岁，于2017年5月前因乳房疼痛不适，在外院检查发现乳腺癌，病理活检诊断为非特殊性浸润癌，ER(-),PR(-),HER2(-)，行全身检查，准备手术治疗，检查发现颅内多发占位，考虑乳癌脑转移，预后不佳，不建议乳癌手术治疗，给予相关保守治疗。后经几次放疗，效果不佳，患者渐渐意识状况下降，经综合考虑，患者家人要求免疫治疗。2018年3月在我院进行免疫治疗，经过3个多月治疗患者脑内肿瘤未见明显增大，患者各种神经系统症状均予以改善，KPS评分值提高。

F(D)=UDiag(f(σ(D)))VT.

σ(D)为矩阵D的奇异值，对称函数f:Rn→R定义如下：

对于τ>0，ε>0，标量函数φ:R→R表示如下：

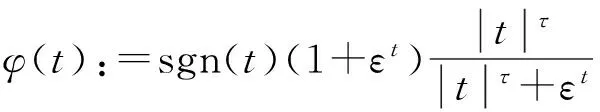
其中sgn(t)为符号函数，定义如下：

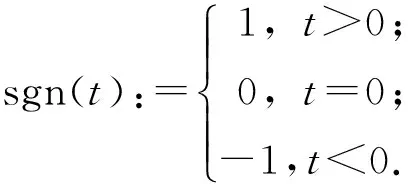
(14)

针对张量秩校正模型，下面给出两阶段张量秩校正方法：

3 算法求解及收敛性分析

3.1 算法求解

在本节中，应用近似点算法(PPA)求解式(11)和式(13).

问题(13)通过转化为式(14),应用近似点算法(PPA)求解.

式(14)的拉格朗日函数为：

则近似点算法(PPA)求解：

(15)

其中γ∈(0,2)，r·s>1.

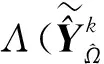
(16)

(17)

(18)

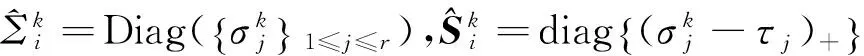
(19)

由于式(15)是在傅里叶域里求解式 (14)矩阵核范数最小化问题.然而原问题式(13)是在实数域里的结果，并且变量都是以张量形式计算.考虑到逆傅里叶变换和张量奇异值分解(t-SVD)的思想，在每一步迭代中应用如下步骤：

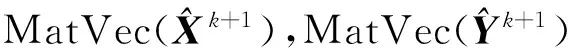
通过上述变换，则可以把矩阵迭代过程转换为张量迭代过程：

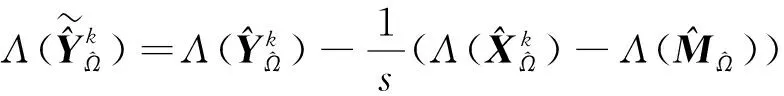
(20)

将式(20)里的矩阵形式转化为张量形式，并还回实数域：

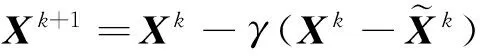
(21)

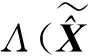
(22)

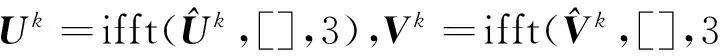
综上，得出求解问题(12)的近似点算法(PPA)如下：

算法3.1

任取γ∈(0,2)，及r·s>1，对给定(Xk,Yk) ，

.(23)

2)松弛步：新的迭代步，

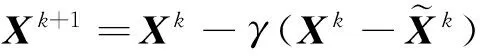
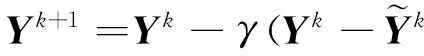
(24)

3.2 收敛性分析

定理3.1 设{Xk,Yk}为由算法3.1产生的迭代序列，若γ∈(0,2)，及rs>1，则序列{Xk,Yk}收敛到问题(13)的鞍点.

证明 对于矩阵求解问题，由He[8]定理3.7分析，当k→时，易知：

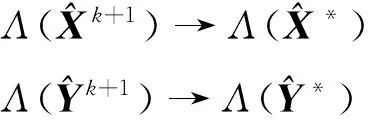
(25)

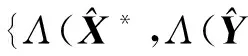
(26)

由于快速傅里叶变换和逆快速傅里叶变换均为连续有界算子，故有：

(27)

取MatVec(Xk+1),MatVec(X*),MatVec(Yk+1)以及MatVec(Y*)分别表示circ(Xk+1),circ(X*),circ(Yk+1),和circ(Y*)的第一列块循环矩阵，并作fold变换.则得到：

(28)

X*和Y*为(13)的鞍点.

证毕.

4 仿真实验

本文针对医学图像和视频图像的恢复问题，分别对张量核范数加权和模型(TSN模型)式(10)、张量核范数最小化模型(TNN模型)式(11)以及张量秩校正模型(CRTNN模型)式(13)进行仿真实验，TSN模型采用HaLRTC方法求解，TNN模型和CRTNN模型采用近似点算法(PPA)求解，并给出仿真结果，所有结果都是在Core i5 的CPU及4G内存的Windows 7系统下的ASUS笔记本中运行MATLAB R2012b计算得出.图像恢复的数值评价指标通常由相对误差和峰值信噪比(PSNR)计算，相对误差计算公式：

(29)

式中：M为实值张量；X为预估张量，峰值信噪比计算公式：

(30)

式中：n1，n2，n3为张量M∈Rn1×n2×n3的维数，同时终止条件为：

(31)

tol为终止参数，取tol=10-3，主要是小于这个值之后，变化特别微小.

文中选取的图像为大小415×477×3的医学图像，视频图像为大小112×160×3的视频的其中一帧，进行仿真实验，并比较TSN模型，TNN模型，CRTNN模型的恢复效果.

图1为医学图像和视频图像原始图像.图2,图3分别为医学图像和视频图像在样本率为20%(即有效信息只有20%)的情况时用TSN模型，TNN模型，CRTNN模型视觉恢复效果对比，从图2，图3的PSNR值对比和视觉恢复效果对比中，可以发现本文提出的CRTNN模型能得到更好的恢复效果.

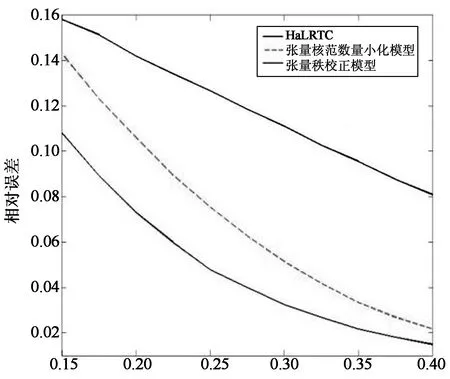
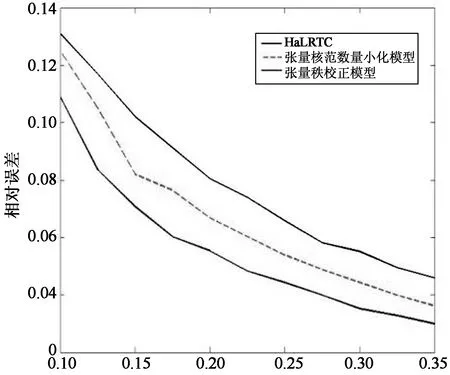
图4分别为医学图像和视频图像在TSN模型，TNN模型，CRTNN模型下对不同样本率得到的相对误差曲线对比．从中可以明显看出：本文提出的张量秩校正方法对不同的样本率得到的恢复图像的相对误差曲线都是最低的，表明本文提出的CRTNN模型能够取得更高精度的恢复效果.

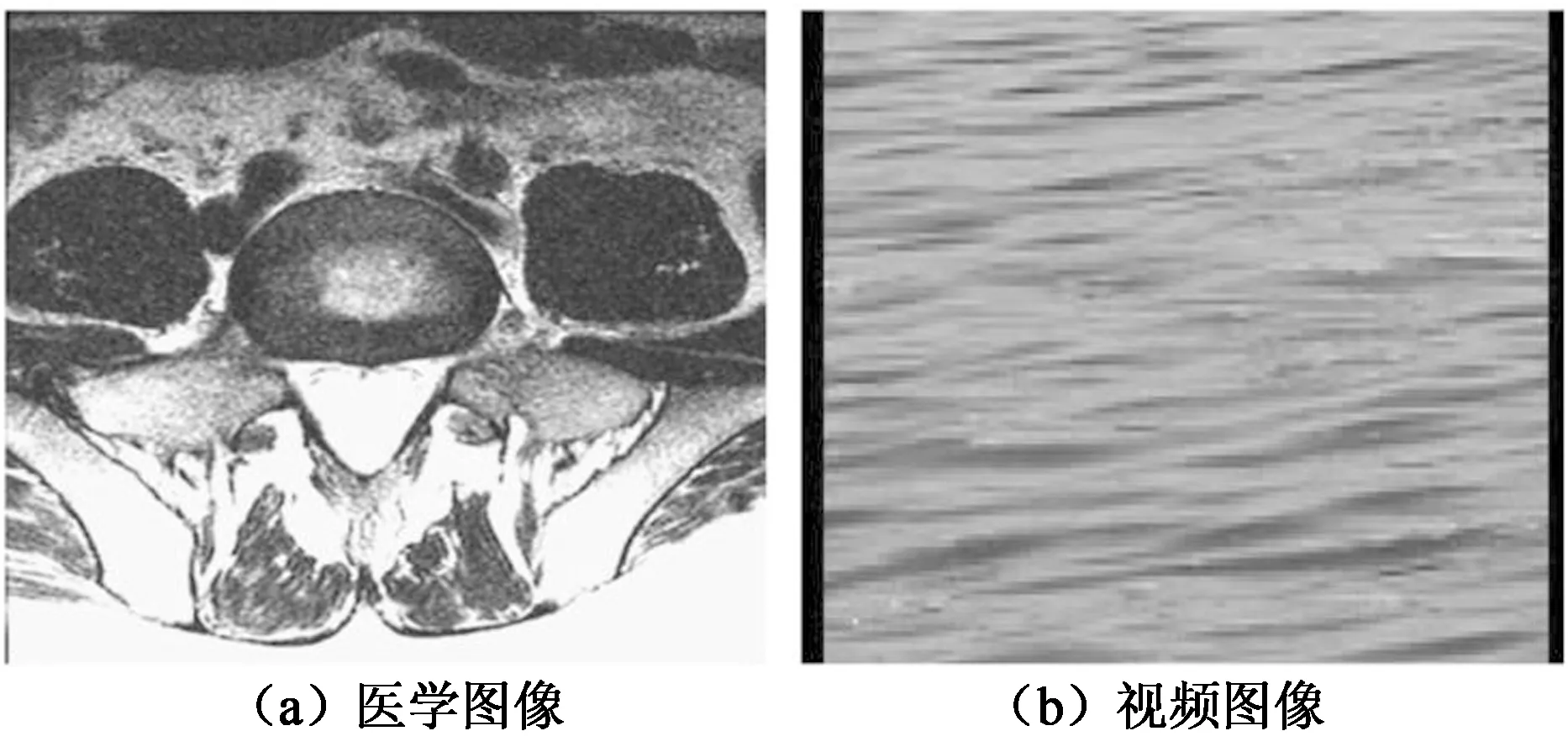
图1 原始图像

图2 样本率为20%的医学图像及其分析在TSN模型，TNN模型和CRTNN模型下的恢复图

Fig.2 Recovery results on a medical image with 20% sample ratio by models TSN,TNN and CRTNN, respectively

图3 样本率为20%的视频图像及其分别在TSN模型，TNN模型和CRTNN模型下的恢复图

Fig.3 Recovery results on a video image with 20% sample ratio by models TSN, TNN and CRTNN, respectively

(a)医学图像结果

(b)视频图像结果

5 结 论

针对高维图像恢复问题，本文提出了张量秩校正模型和两阶段张量秩校正方法，并提出了求解张量秩校正模型的张量近似点算法，从理论上分析了该算法的收敛性.仿真结果验证了本文所提出模型和方法的有效性，结果表明，张量秩校正方法模型能够取得更高的恢复精度.能否将该模型和算法推广到四阶及以上的图像恢复问题？这个问题值得进一步研究.

[1] ELY G, AERON S, MILLER E L. Exploiting structural complexity for robust and rapid hyper spectral imaging [C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2013：2193-2197.

[2] GANDY S, RECHT B, YAMADA I. Tensor completion and low-n-rank tensor recovery via convex optimization [J]. Inverse Problems, 2011, 27(2): 025010.

[3] HAO N H, KILMER M E, BRAMAN K, et al.Facialrecognitionwithtensor-tensordecompositions[J].SIAMJournalonImagingSciences, 2013， 6(1): 437-463.

[4]KILMERM,BRAMANK,HAON,et al.Third-ordertensorsasoperatorsonmatrices:Atheoreticalandcomputationalframeworkwithapplicationsinimaging[J].SIAMJournalonMatrixAnalysisandApplications, 2013, 34(1):148-172.

[5]LIUJ,MUSIALSKIP,WONKAP, et al.Tensorcompletionforestimatingmissingvaluesinvisualdata[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2013, 35(1): 208-220.

[6]SEMERCIO,HAON,KILMERME,et al.Tensor-basedformulationandnuclearnormregularizationformultienergycomputedtomography[J].IEEETransactiononImageProcessing, 2014, 23(4): 1678-1693.

[7]MUC,HUANGB,WRIGHTJ,et al.Squaredeal:Lowerboundsandimprovedrelaxationsfortensorrecovery[C]//Proceedingsofthe31stInternationalConferenceonMachineLearning(ICML-14), 2014, 32(1): 73-81.

[8]HEBS,YUANXM,ZHANGWX.Acustomizedproximalpointalgorithmforconvexminimizationwithlinearconstraints[J].ComputationalOptimizationandApplications, 2013, 56(3): 559-572.

[9]TOHKC,YUNS.Anacceleratedproximalgradientalgorithmfornuclearnormregularizedleastsquaresproblems[J].PacificJournalofOptimization, 2010, 6(3): 615-640.

[10]KILMERME,MARTINCD.Factorizationstrategiesforthird-ordertensors[J].LinearAlgebraanditsApplications, 2011, 435(3):641-658.

[11]MIAOW,PANS,SUND.Arank-correctedprocedureformatrixcompletionwithfixedbasiscoefficients[J].Math.Programming，2016，159(1)：289-338.

[12]ZHANGZ,ELYG,AERONS,et al.Novelmethodsformultilineardatacompletionandde-noisingbasedontensor-SVD[C]//InProceedingsoftheIEEEConferenceonComputerVisionandPatternRecognition(CVPR), 2014, 3842-3849.

[13]CAIJF,CANDESEJ,SHENZ.Asingularvaluethresholdingalgorithmformatrixcompletion[J].SIAMJournalonOptimization, 2010, 20(4): 1956-1982.

Tensor Rank Corrected Procedure for Image Restoration

BAI Min-ru†,HUANG Xiao-long,GU Guang-ze,ZHAO Xue-ying

(College of Mathematics and Econometrics, Hunan Univ, Changsha, Hunan 410082, China )

Tensor-based restoration of medical images and video images was studied with limited samples. On the basis of the theory of tensor singular value decomposition (t-SVD), a tensor rank-correction model (CRTNN) was proposed to correct the tensor nuclear norm minimization model (TNN). A two-stage rank correction method is given as follows: the first stage is used to generate a pre-estimator by solving the TNN model, and the second stage is to solve the CRTNN model to generate a high-accuracy recovery by the pre-estimator. A tensor proximal point algorithm was proposed to solve the CRTNN model and the TNN model, making it possible to calculate tensor directly in the real field. The convergence of the algorithm was proved in theory. Numerical experiments of medical images and video images verify the efficiency of the proposed model and method. The experiment results show that tensor rank-correction model and method can achieve higher-accuracy recovery.

image restoration；t-SVD; tensor rank-correction model; tensor proximal point algorithm

1674-2974(2016)10-0148-07

2016-01-17

国家自然科学基金资助项目(11571098)， National Natural Science Foundation of China(11571098) ； 湖南省高校创新平台开放基金资助项目(14K018)

白敏茹(1968-)，女，江西宜春人，湖南大学博士生导师, 副教授

†通讯联系人，E-mail:minru-bai@163.com

TP751

A