面向液压挖掘机电控多路阀的控制系统参数整定

王安麟,田光伟,李晓田

(同济大学 机械与能源工程学院，上海 201804)



面向液压挖掘机电控多路阀的控制系统参数整定

王安麟*,田光伟,李晓田

(同济大学 机械与能源工程学院，上海 201804)

针对传统液压挖掘机多路阀结构与整机性能间的耦合、液压控制系统精度低带来的整机控制不匹配问题，为实现液压挖掘机多路阀简单化设计和整机控制系统自适应变化，提出面对液压挖掘机电控多路阀的控制系统参数整定方法.界定操纵电手柄输出为0-1数字信号，考虑整机多路阀结构特征，设计液压挖掘机电控多路阀的变参数一阶控制系统，提出综合系统冲击、能量利用率、跟随性三项指标作为参数整定的评价算法.通过设计电手柄-控制器-液压挖掘机整机性能表达的数字化平台三者衔接的半物理仿真平台进行试验，分析结果表明：控制系统有效，且控制器响应的一阶控制系统参数T、K可基于整机性能整定得出；时间常数T可由电控多路阀阀芯固有频率和阀芯开度决定，与阀芯阻尼比相关度较小.

控制系统；液压挖掘机；数字化平台；性能；时间常数

液压挖掘机在土方建筑机械中扮演着一个至关重要的角色，其高效作业有助于快速、节能地完成施工计划[1].然而，液压挖掘机作业工况复杂恶劣、载荷波动剧烈，且多路阀阀芯结构与其性能存在很大关联，设计复杂.另外，液压控制系统精度低也是影响液压挖掘机整机控制性能的一个直观因素.经验丰富的操作人员通过控制手柄可以实现较为理想的作业，但是人为因素大，操作强度高，操作人员容易疲劳.因此，简化多路阀结构，并从设计制造到应用全过程，设计整机性能高、操作便捷的液压挖掘机系统与控制策略将具有重要意义.目前国内外对液压挖掘机的研究很多，其中主要包括有先进控制策略[2-3]、混合动力[4]，以及对传统元件的再设计[5].但这些研究尚存在的缺陷在于：基于发动机-泵-负载之间的功率匹配未考虑操作人员在操作手柄开启或关闭过程中由多路阀带来的动态性能影响.同时，随着电子计算机技术和信息控制技术的迅速发展，现代挖掘机先导控制系统可以由电、磁等形式来完成相应动作，避免受先导管路阻力的影响，提高响应速度和控制精度.文献[6-7]研究液压挖掘机节能控制技术时，设计采用电手柄控制多路阀，即由电手柄产生信号，通过比例放大器和系统回路，产生电磁力或液压先导力作用于多路阀阀芯.其研究结果表明：采用电控技术和合适的控制策略，可以达到节能的效果.但是从操作人员发出操作指令到作用于整机过程，其中缺少优化环节，且控制指令是模拟信号，操作量需要人掌控，必然增加了操作强度.因此，有必要根据液压挖掘机整机模型特性开展控制响应过程对系统性能影响的研究.

为实现上述目的，本文用电磁比例多路阀替换传统结构复杂的液控多路阀，提出面对液压挖掘机电控多路阀的控制系统参数整定方法.研究液压挖掘机控制系统的控制参数、电控多路阀特征、整机系统三者之间的影响关系，期望在一定程度上为提高整机性能、以及设计模型与电控系统之间的自适应性提供依据.

1 液压挖掘机整机性能表达的数字化仿真平台

本研究主要分析液压挖掘机工作臂和旋转部分工作特性，铲斗内可以加载土壤，不考虑加载挖掘力影响.为了实现数字化分析仿真，通过VB编程搭建液压挖掘机整机性能表达的数字化平台.

液压挖掘机的工作过程呈现循环往复周期性特点，其一个工作循环的主要工况构成为：挖掘工况 、满斗举升回转工况、卸载工况、空斗返回工况.但是不论哪种工况，分解开来主要是由液压挖掘机4个执行元件来完成，即铲斗、斗杆、动臂、回转.其每一执行元件动作都是由一个发动机、泵、管道、多路阀、执行元件组成的系统回路，不同的是多路阀结构和数量.鉴于多路主阀是实际整机工作过程中的核心元件，整机动态特性和静态特性影响多路主阀性能与结构[8-9].所以在本研究中，以20 t液压挖掘机系统为例，将原液压挖掘机系统的液控多路阀用电磁比例多路阀代替，阀芯驱动力为电磁力，改变输入电流大小，从而控制多路阀开度和流量.下面就单动作铲斗工况下铲斗主阀结构和流量建模进行探究，其他工况下主阀分析建模类似于单动作铲斗工况，在此不作阐述.

铲斗主阀结构和内部液压油路建模如图1所示，每个阀口看作为一个节流阀.

图1 铲斗主阀建模示意图

根据节流口处的压力-流量方程，可以得出多路阀各阀口处的流量方程，如QP-A表示为式(1)，其他各阀口处的流量方程同理：

(1)式中:QP-A为P口到A口的液压油流量； PP为多路阀P口压力；PA为多路阀A口压力；Cd为流量系数；ρ为液压油密度；f为相应阀口间的开口面积.

基于上述分析，将节流阀阀口两端的压差定义为阀口压降Δp0，Bar；同时标定压降对应的流量为Q0，L/min；f0为相应阀口全开时的开口面积；x0为阀芯开度.则有：

(2)

理论上，流量系数Cd由节流口形状、流体状态、流体性质等因素决定，开口面积f与阀芯形状有关，一般难以确定，需由试验得出.

当铲斗主阀为滑阀时，开口面积Q与阀芯开度成正比.则由式(2)可推导出阀口位移变化时的流量Q与压降之间的关系为

(3)

所以，在构建液压挖掘机整机性能表达的数字化平台中，通过试验标定出阀口压降Δp0和对应流量Q0后，阀口流量可直接由阀口两端的压降和阀芯位移得出，避免流量系数Cd、开口面积f难以确定的问题，简化了数字化平台上构建不同结构的多路阀的过程.另外，已知铲斗油缸的大、小腔面积，根据阀口流量Q得到铲斗油缸的压力变化曲线.

根据上述分析，建立其他工况下多路阀数字化模型.同时，根据文献[7]，建立液压挖掘机整机系统其他部分，如机械部分、传动部分，最终得到液压挖掘机整机性能表达的数字化平台，如图2所示.

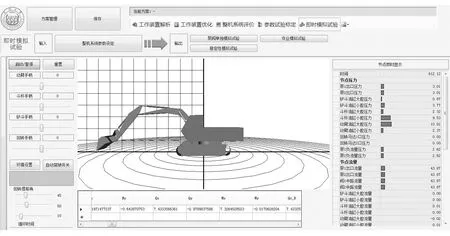
图2 液压挖掘机整机性能表达的数字化平台

本平台是在和国内某公司产学研合作下完成，为验证平台的正确性，利用AMESim软件建立同样的机械模型对比，其仿真模型图见文献[10]，仿真如图3所示液压挖掘机某一挖掘复合工况，所得对比结果如图4所示.

图3 仿真的动作工况

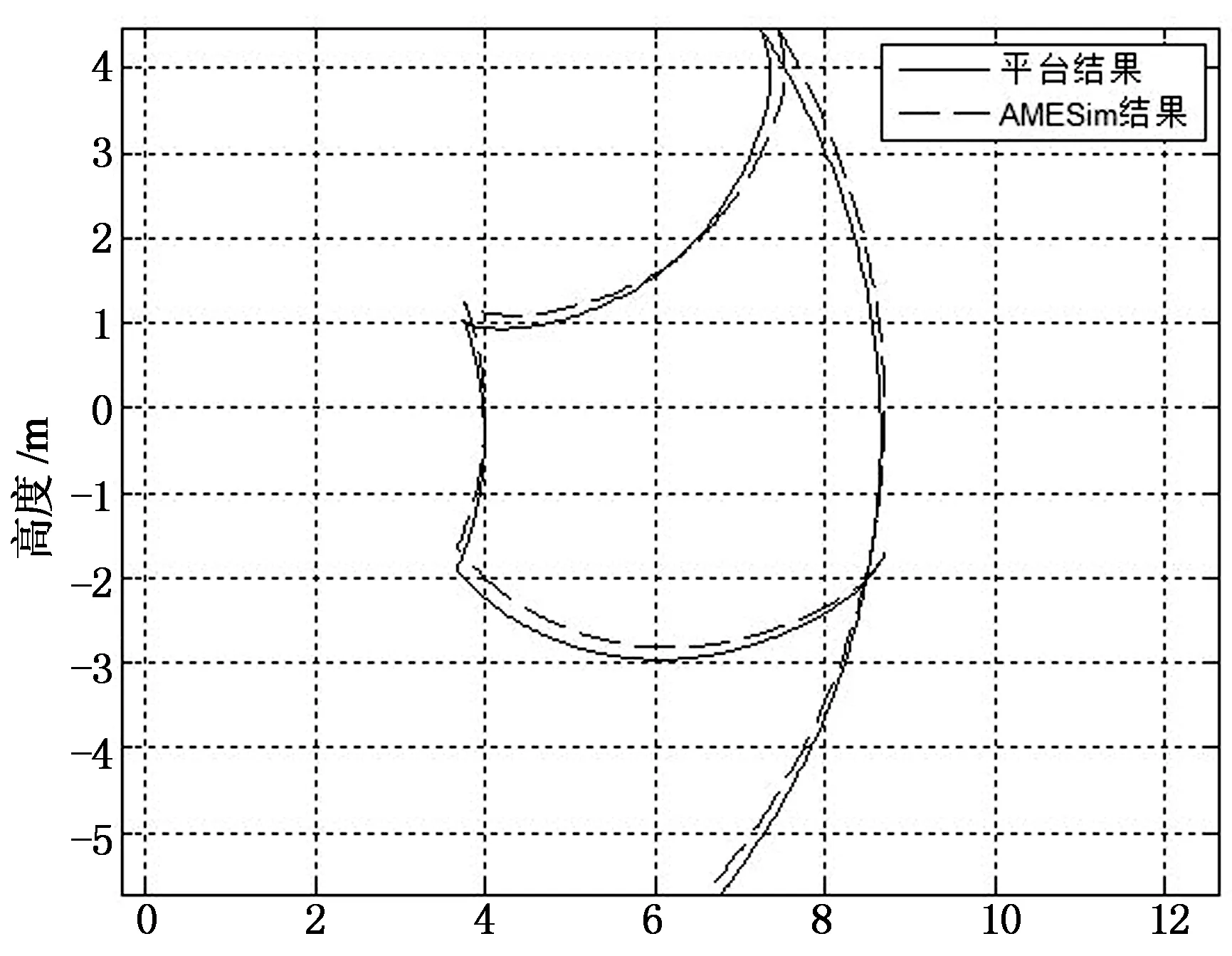
宽度/m

文献[11]和图4可以表明，利用键合图理论所构建的液压挖掘机整机性能表达的数字化平台和AMESim结果具有一致性，实现了液压挖掘机机电液大系统的一体化解析、优化、仿真.误差主要来源于AMESim模型中关节之间假定是刚性接触，而在本研究中的关节之间采用的是一个弹簧阻尼系统.

2 电控多路阀的控制系统设计

根据液压挖掘机整机控制结构，设计液压挖掘机电手柄控制系统，其电手柄输出0-1指令信号，具体控制过程如图5所示.

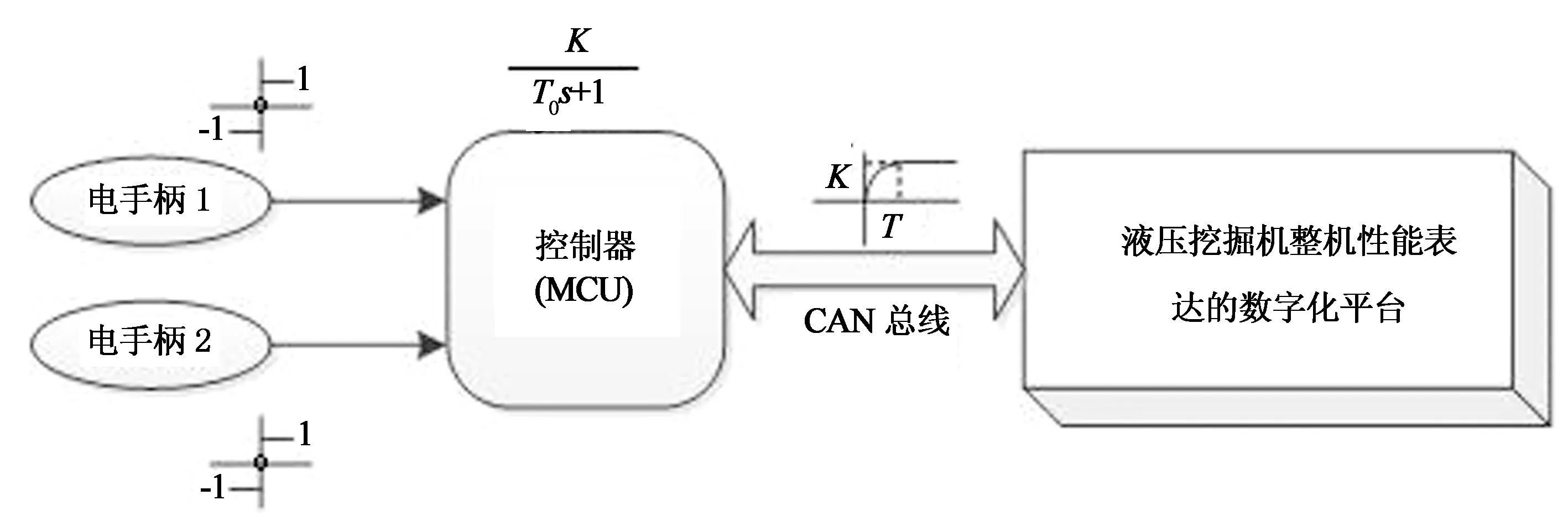
图5 面向液压挖掘机电控多路阀的控制系统

当操作人员操作电手柄时，液压挖掘机控制器得到操作者需要操作某一执行元件的信号.理论上，液压挖掘机从开始位置到理想响应位置需要一个时间过程，但是时间T对系统的性能有一定的影响.若T过小，将会对系统执行元件造成冲击；而T过大，系统达到理想响应时间过程过长，影响作业效率.另一方面，时间T对系统执行元件获能也存在影响.因此，拟设计一阶液压挖掘机控制器，其控制函数G(s)为：

(4)

式中：T0,K分别为控制系统时间常数和稳态值.

鉴于控制器输出响应信号直接作用于整机电控多路阀，且多路阀为整机核心元件，故本研究主要探讨液压挖掘机电控多路阀特征与控制系统的关系.液压挖掘机控制器在得到操作人员操作指令后，结合当前液压挖掘机电控多路阀特征，合理优化时间常数T0，使之合理过渡达到稳态值K，从而使系统性能较优.另一方面，为降低操作人员劳动强度，所设计的控制系统从两个方面出发考虑：一是稳态值K设置为多路阀阀芯开度x0；二是手柄输入为0-1数字指令信号，即1代表某执行元件动作，0代表液压挖掘机工作机构不动作.此时，操作人员只需要发送操作指令即可，而不需要操纵控制量.而控制系统的时间常数T0可由控制器根据后续评价指标整定得到.

根据单位一阶信号特征[12]，系统过渡响应时间一般取T=4T0，即时间常数T0和系统响应时间T成比例关系.为形象直观化，后续论述控制系统的时间常数采用响应时间T表征，所得结果实质上只取1/4大小.

3 电控多路阀系统的设计评价

在液压整机系统中，系统冲击、能量利用率、跟随性常作为评价指标，所以在本研究中，综合选取上述3个系统响应量作为液压挖掘机性能评价指标，结合整机电控多路阀特性进行半物理仿真分析，整定得到控制器控制系统的时间常数T.

3.1 系统冲击

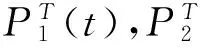
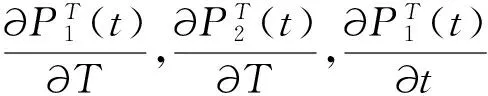
3.2 能量利用率

3.3 跟随性

控制响应时间常数T决定整机多路阀从开启到工作、或工作到关闭过程持续的时长以及特性，整机油缸活塞位移或者旋转马达角度也存在差异.在本研究中，设定相同的作业时间，控制器改变响应时间常数T，若对位移量或角度影响较大，则显然不满足操作目标要求，即“跟随性”差.

3.4 评价算法

综合上述3个性能评价指标来确定响应时间常数T，显然其是一个多目标优化问题.具体评价算法步骤如下：

步骤1 针对某一工况，设置时间常数T变化区间[Ti,Tj]；

步骤2 利用数字化平台，生成系统评价指标响应曲线；

步骤3 基于跟随性指标，以STi(t)或θTi(t)曲线为基准，求得在最大位移误差为δ下时的时间常数T区间为[Ti,Tg](注：仿真试验中设定δ=5%)；

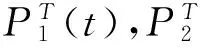
步骤5 基于能量利用率的原则，根据步骤3所得区间和步骤4所确定时间参数点附近，求取ηT最大点Tk，即Tk为液压挖掘机最优控制响应时间常数.

4 电控多路阀控制系统的仿真与其参

数整定4.1 仿真参数设定

根据上述分析，基于液压挖掘机整机性能表达的数字化平台搭建半物理仿真试验平台，对某一型号液压挖掘机进行仿真分析，其有关主要参数如表1所示.且设定仿真时间为18 s，发动机设定工作在H档，整机为负流量控制系统.

仿真试验分A，B，C和D 4种工况.电控多路阀阀口压降受阀芯结构、阀口开度等因素决定，在数字化平台上仿真试验设定如表2所示．滑阀阀芯固有频率为40 Hz，阀芯阻尼比为1，阀芯开度x0为1 cm.

表1 某一型号液压挖掘机主要参数

4.2 仿真结果

当操作人员操作电手柄，向控制器发出指令信号后，控制器根据电控多路阀特性确定响应时间常数T.其仿真设定工况如图6所示，即设定工作时间持续3 s，响应时间Ti(i取1,2,3,4)由液压挖掘机控制器调节控制.

图6 仿真工况设定

本文中探究T1，T2，T3和T4变化一致时的控制系统，其仿真系统原理图如图7所示.结合第2节分析，考虑T在[0.05，2.00]范围内变化，且每次仿真时间常数T的增量ΔT为0.05 s，按如下试验步骤进行仿真：

步骤1 初始化.包括仿真工况设定、整机模型状态和电控多路阀参数，使得当操作电手柄发出0-1信号时，控制器可根据初始化条件识别A,B,C,D电控多路阀控制系统.

步骤2 控制器控制参数设定.设定电控多路阀控制系统仿真响应时间常数T为0.05 s，稳定值K为阀芯开度x0

步骤3 启动仿真.完成该次仿真，并记录保存各评价指标的结果.

步骤4 更新控制环节参数.即改变时间参数T为0.05+n×ΔT，其n为仿真次数.

步骤5 仿真判定.保持仿真工况设定不变，初始化整机模型，若T不大于2 s，则返回步骤3，继续进行仿真试验；若T大于2 s，则终止仿真试验.

步骤6 基于上述多次仿真试验得到的结果，按给定评价算法，可整定得到A,B,C,D电控多路阀控制系统的最优控制响应时间常数Tk.

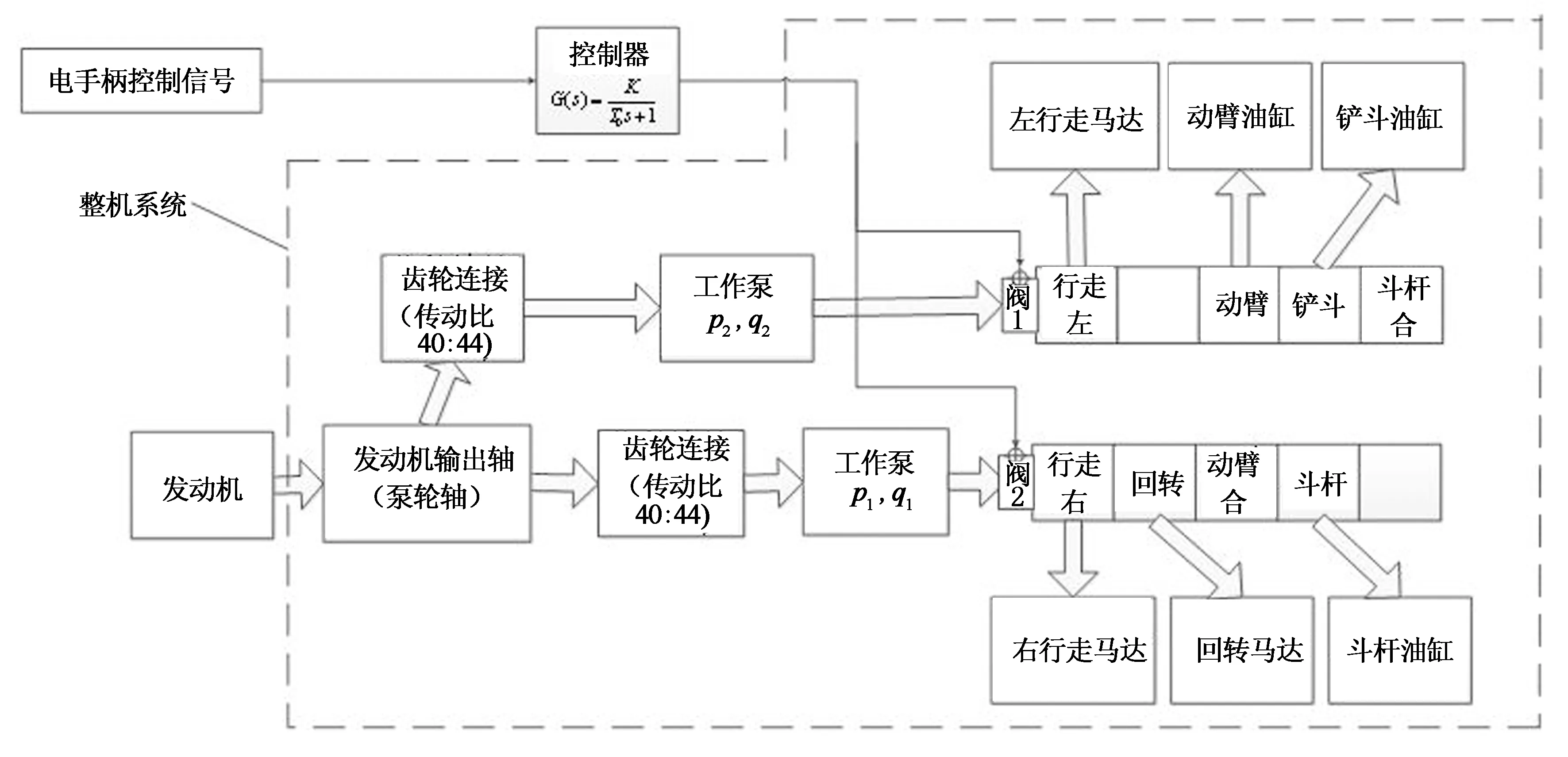
图7 仿真系统原理图

其仿真结果如图8～11所示，根据评价算法计算得出A,B,C,D 4种工况下的时间常数最优值分别为1.05 s,0.95 s,0.9 s,0.95 s.对比图8～11可以看出：A工况下，当T=1.05 s时，铲斗缸获能百分比最高，此时铲斗缸大、小腔压力变化较优，而铲斗活塞位移相对T变化不大，跟随性满足要求.同理于B工况下，当T=0.95 s时，液压挖掘机性能最优.C工况下，动臂缸获能百分比、动臂缸大腔压力变化、以及动臂活塞位移相对T变化都不大，但在T=0.9 s时，动臂缸小腔压力变化较优.而对于D工况下，回转角度和回转马达获能随T的增大而增大，为保证跟随性，T取0.95 s较优.

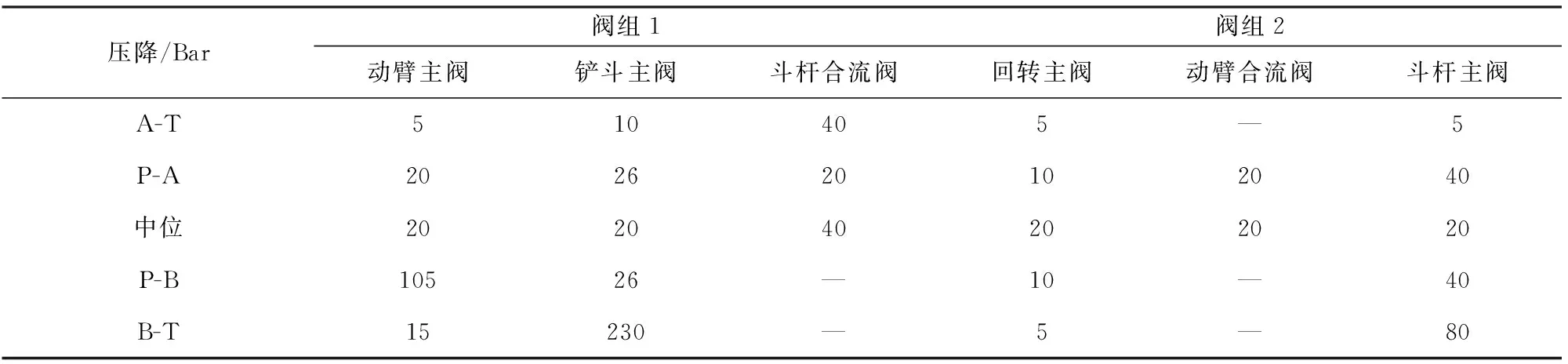
表2 多路阀阀口压降

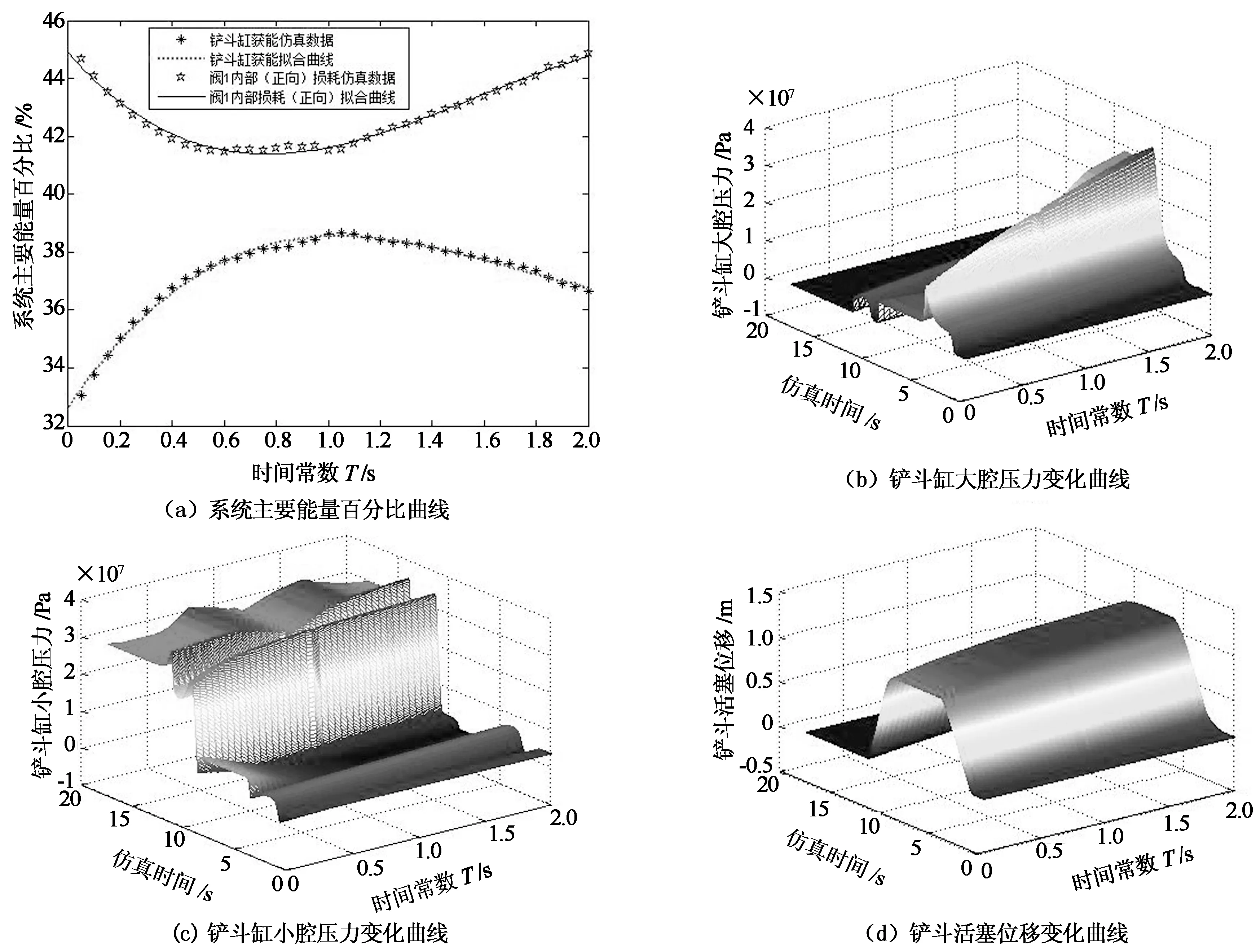
图8 A工况下时间常数T变化时系统性能

图9 B工况下时间常数T变化时系统性能

图10 C工况下时间常数T变化时系统性能

图11 D工况下时间常数T变化时系统性能

改变多路阀阀芯主要参数，即阀芯开度、阻尼比，以及固有频率，再次仿真分析，可得到此时系统对应的整机最优响应时间常数如表3～表5所示.

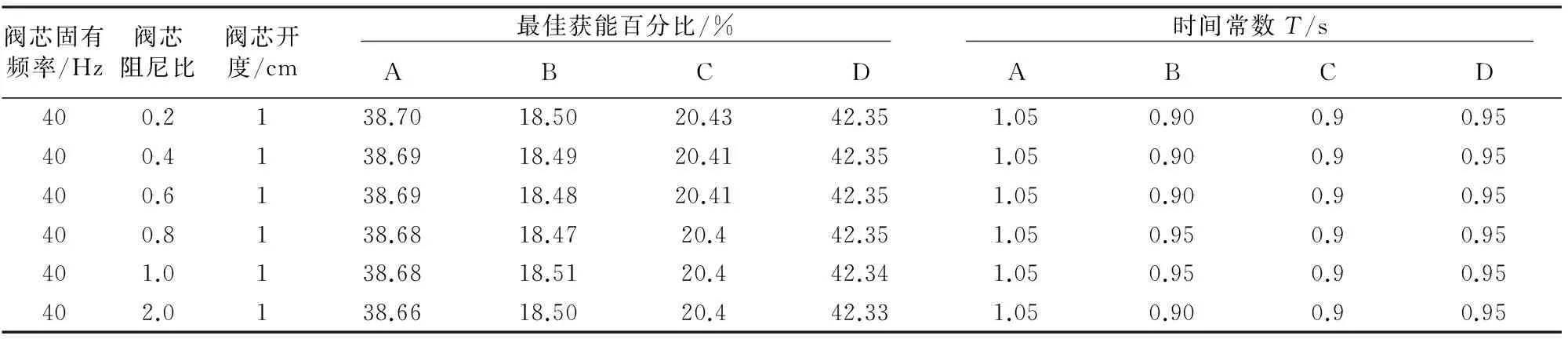
表3 响应时间常数T与阀芯阻尼比关系

表4 响应时间常数T与阀芯开度关系

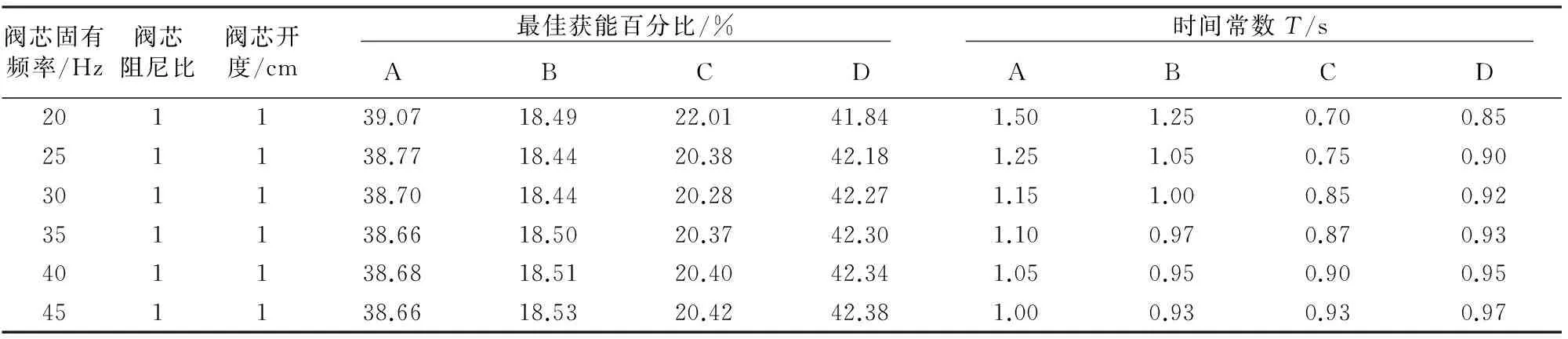
表5 响应时间常数T与阀芯固有频率关系

由表3～表5仿真结果可以发现：整机系统中的电控多路阀其阀芯阻尼比与控制器响应时间常数相关度较小，主要是阀芯开度和阀芯固有频率会影响控制器响应时间常数确定；另一方面，改变阀芯开度和阀芯固有频率，控制器输出响应时间常数呈规律性变化.

因此，面向液压挖掘机电控多路阀的控制系统可以在一定程度上解决液压挖掘机从整机机械设计到电控系统设计过程中的参数整定问题，弱化多路阀与整机性能的耦合，改善操作人员操作强度，提高整机匹配性能.

5 结 论

1)针对当前液压挖掘机控制系统存在操作强度大、多路阀结构耦合等问题，实现液压挖掘机多路阀简单化设计和整机控制系统自适应变化，本研究采用电手柄与电磁比例多路阀，提出了面向液压挖掘机电控多路阀的控制系统参数整定方法.并利用基于液压挖掘机整机性能表达的数字化平台搭建的半物理仿真试验证明了该方法的可行性.

2)本研究设计的控制系统相关参数主要是控制器输出一阶信号的时间常数T和稳态值K，其评价方法综合包括系统冲击、能量利用率、跟随性.设定K等于电磁比例多路换向阀阀芯开度x0，时间常数T面向液压挖掘机电控多路阀特性(即：阀芯固有频率、阻尼比、阀芯开度)整定得到.仿真结果表明：时间常数T可主要由多路阀阀芯开度和阀芯固有频率确定，且在不同工况下呈现规律性变化；而阀芯阻尼比与其相关度较小.

3)本文以电控多路阀液压挖掘机的整机控制性能为研究对象，实现了整机多路阀设计、电控操作、整机性能三者之间的一体化匹配，其研究方法与思想对同类问题具有借鉴性.

[1] BENDER F A, SONNTAG M, SAWODNY O. Nonlinear model predictive control of a hydraulic excavator using Hammerstein models[C]// Proceedings of the 6th International Conference on Automation, Robotics and Applications. Queenstown, New Zealand :IEEE , 2015: 557-562.

[2] PARK J, CHO D, KIM S,etal. Utilizing online learning based on echo-state networks for the control of a hydraulic excavator[J]. Mechatronics，2014, 24(8): 986-1000.

[3] KIM Y B, HA J, KANG H,etal. Dynamically optimal trajectories for earthmoving excavators[J]. Automation in Construction，2013, 35(4): 568-578.

[4] 刘昌盛,何清华, 龚俊,等. 液压挖掘机混合动力系统节能特性及试验研究 [J]. 湖南大学学报：自然科学版,2015,42(8):40-46.

LIU Chang-sheng , HE Qing-hua , GONG Jun，etal. Energy saving performance and experimental study on hybrid system of hydraulic excavator[J]. Journal of Hunan University: Natural Sciences, 2015,42(8): 40-46. (In Chinese)

[5] CASOLI P, ANTHONY A. Gray box modeling of an excavator’s variable displacement hydraulic pump for fast simulation of excavation cycles[J]. Control Engineering Practice，2013, 21(4): 483-494.

[6] 王炎. 液压挖掘机负荷传感系统的仿真研究及节能分析[D]. 长沙:中南大学机电工程学院, 2009：21-27.

WANG Yan. Simulation research and energy analysis of hydraulic excavator with load-sensing system[D].Changsha: College of Mechanical and Electronic Engineering，Central South University, 2009:21-27． (In Chinese)

[7] 林慕义, 史青录. 单斗液压挖掘机构造与设计[M]. 北京:冶金工业出版社,2011:428-434.

LIN Mu-yi, SHI Qin-lu. Construction and design of single bucket hydraulic excavator[M]. Beijing: Metallurgical Industry Press, 2011:428-434. (In Chinese)

[8] 高峰. 液压挖掘机节能控制技术的研究[D]. 杭州:浙江大学机械工程学院, 2002:41-46.

GAO Feng. Study on energy-saving control technology of hydraulic excavator[D]. Hangzhou: College of Mechaincal Engineering， Zhejiang University, 2002:41-46．(In Chinese)

[9] 王丽薇, 吕晓林. 基于ITI-SimulationX的液压挖掘机多路阀建模与仿真[J]. 机床与液压, 2012,40(9): 126-134.

WANG Li-wei, LV Xiao-lin. Modeling and simulation of multi-way valve in hydraulic excavator based on ITI-SimulationX[J]. Machine Tool & Hydraulics,2012,40(9):126-134. (In Chinese)

[10]王安麟,石世宁. 基于响应面法的中型挖掘机模型参数标定[J]. 机械设计, 2013,30(7):59-63.

WANG An-lin, SHI Shi-ning. Parameter calibration for medium excavator model based on response surface methodology[J]. Journal of Machine Design,2013,30(7):59-63. (In Chinese)

[11]XIAOTIAN L, ANLIN W. Definitions of causality in bond graph model for efficient simulation mechanism[J]. Mechanism and Machine Theory,2014, 80(10): 112-124.

[12]杨叔子,杨克冲,吴波，等. 机械工程控制基础[M]. 武汉:华中科技大学出版社,2011:82-83.

YANG Shu-zi, YANG Ke-chong, WU Bo,etal. Mechanical control engineering fundamentals[M]. Wuhan: Huazhong University of Science and Technology Press, 2011:82-83.(In Chinese)

Parameter Turning of Control System Based on Electronically Controlled Multi-valve of Hydraulic Excavator

WANG An-lin†，TIAN Guang-wei，LI Xiao-tian

(College of Mechanical Engineering, Tongji Univ, Shanghai 201804, China)

Aimingat on the coupling between the multi-valve structure of the conventional hydraulic excavator and the machine performance，the no-matching problem of machine control generated by the low precision of hydraulic control system, a parameter turning method of control system based on electronically controlled multi-valve of hydraulic excavator was proposed to achieve simplified design of hydraulic excavator multi-valve and adaptive change of the machine control systems. The output of electrical control handles was defined as 0-1 digital signal. Considering the structural characteristics of the multi-valve，the first-order control system of variable parameters for electronically controlled multi-valve of the hydraulic excavator is designed. An evaluating algorithm of parameter tuning was put forward, combining the system shock，energy efficiency，and the following performance. By designing hardware-in-Loop simulation, which is formed of the electrical control handles, controller, performance digital platform of hydraulic excavator, it shows that the control systems are effective, and the parameterTandKof the first-order control system，which the controller responds to，can base on the machine performance to be tuned. It is also found that time constantTcan be determined by the natural frequency of multi-valve spool and the valve opening，and has smaller correlation with the spool-valve damping ratio. The design method of the hydraulic excavator provides good application value for the machine multi-valve design，which is associated with the design of control and operation.

control systems; hydraulic excavator; digital platform; performance; time constant

1674-2974(2016)10-0052-10

2015-12-23

2012年重大科技成果转化项目(财建[2012]258号)

王安麟(1954-)，男，陕西安康人，同济大学教授，博士生导师

†通讯联系人，E-mail: wanganlin@tongji.edu.cn

TH-39

A