角平分线、平行线与等腰三角形

□苗赛莉

角平分线、平行线与等腰三角形

□苗赛莉

角平分线、平行线与等腰三角形关系密切，在题设中若见其一，应思其二，想其三，这种解题思路往往是打开第一道大门的金钥匙，突破解题的一个难点，使一类题目变难为易成为可能.这种思维方法称为“知识板块”思维法.

为帮助大家更好理解，现作如下归纳：

1.角平分线遇平行线出现等腰三角形.

①直线与角的一边平行出现等腰三角形.

如图1，已知：O D平分∠A O B，C D∥O A，则可得△O C D为等腰三角形.

图1

②直线与角的平分线平行出现等腰三角形.

如图2，已知：O C平分∠A O B，O C∥D E，则可得△O D E为等腰三角形.

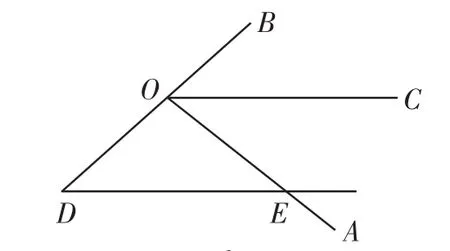
图2

2.等腰三角形与角平分线往往出现平行线.

①等腰三角形的一腰与角的一边出现平行.

如图1，已知：△O C D中，C O＝C D，O D平分∠A O B，则可得C D∥O A.

②等腰三角形的底边与顶角的外角平分线出现平行.

如图2，已知：△O C D中，O D＝O E，O C平分∠A O B，则可得O C∥D E.

3.等腰三角形与平行线往往产生角平分线.

①过一腰的直线与角的一边平行产生角平分线.

如图1，已知：△O C D中，C O＝C D，C D∥O A，则可得O D平分∠A O B.

②过顶角顶点的直线与底边平行产生角平分线.

如图2，已知：△O C D中，O D＝O E，O C∥D E，则可得O C平分∠A O B.

例已知在△A B C中，B D平分∠A B C，过点D作D E∥B C，分别交A B、A C于点E、F，连接C D.

（1）如图3，若C D为∠A C B的平分线，求证：E F＝B E＋C F.

（2）如图4，若C D为∠A C B的外角平分线，试猜想：E F、B E、C F三条线段的数量关系，并验证你的猜想.

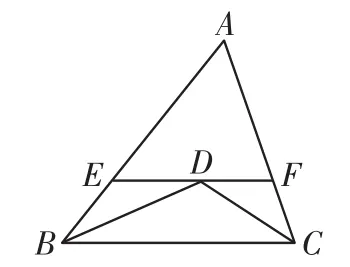
图3

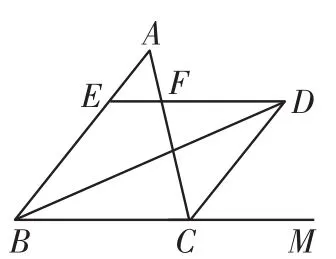
图4

分析：（1）本题中已知条件中有角平分线，还有平行线，利用角平分线和平行线，易知△B D E和△C D F为等腰三角形，得到B E＝D E，C F＝D F，通过等量代换可得E F＝B E＋C F.

（2）虽然C D从△A B C内部移到了外部，但C D还是角平分线，利用平行，结合（1）的思路，易知△B D E和△C D F为等腰三角形，从而得到B E＝D E，C F＝D F.借助E F＝D ED F，可得E F＝B E－C F.

解：（1）∵B D和C D分别为∠A B C和∠A C B的平分线，

∴∠E B D＝∠C B D，

∠F C D＝∠B C D.

∵D E∥B C，

∴∠E D B＝∠C B D，

∠F D C＝∠B C D，

∴∠E B D＝∠E D B，

∠F D C＝∠F C D，

∴B E＝D E，C F＝D F，

∴E F＝D E＋D F＝B E＋C F，即E F＝B E＋C F.

（2）猜想：E F＝B E－C F.

验证：∵B D和C D分别为∠A B C和∠A C M平分线，

∴∠E B D＝∠C B D，

∠F C D＝∠M C D

∵D E∥B C，

∴∠E D B＝∠C B D，

∠F D C＝∠M C D，

∴∠E B D＝∠E D B，

∠F D C＝∠F C D，

∴B E＝D E，C F＝D F，

∴E F＝D E－D F＝B E－C F，

即E F＝B E－C F.

点评：本题中的两问都是由角平分线、平行线发现等腰三角形，并且同时出现两个等腰三角形.利用角平分线和平行线发现等腰三角形是突破此类问题难点的关键.