巧用对称妙构等腰

□朱元生

巧用对称妙构等腰

□朱元生

在解几何题的过程中，若遇有高线、角平分线、线段的垂直平分线，可根据图形的轴对称性，巧妙构造等腰三角形，借助等腰三角形的有关性质，往往能够迅速找到解题途径，直观易懂，简捷明快.

一、图形含有垂线（或高线），以垂线（或高线）为对称轴构造等腰三角形

例1如图1，已知A D⊥B C于点D，且∠B＝2∠C，试说明：A B＋B D＝D C.

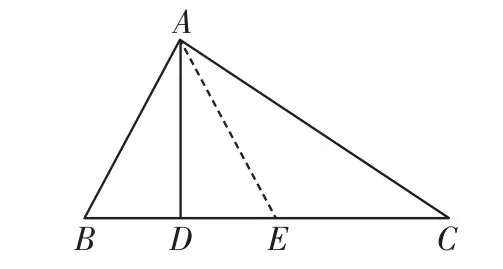
图1

分析：因为A D⊥B C，以A D为对称轴进行变换，点B的对称点E必落在B C上，连接A E，则△A B E为等腰三角形，根据等腰三角形的性质使问题迎刃而解.

解：因为A D⊥B C，以A D为对称轴进行变换，点E为点B的对称点.

连接A E，则△A B E为等腰三角形，所以∠A E B＝∠B＝2∠C，且D B＝D E.

因为∠A E B＝∠C＋∠C A E，

而∠A E B＝2∠C，

所以∠C＝∠C A E，

从而A E＝C E.

因此A B＝A E＝E C

所以A B+B D=E C+D E=D C.

二、图形含有角平分线，以角平分线为对称轴构造等腰三角形

例2如图2，在等腰Rt△A B C中，∠B A C＝90°，∠B的平分线交A C于D，过C作B D的垂线交B D的延长线于E，试说明：B D＝2 C E.

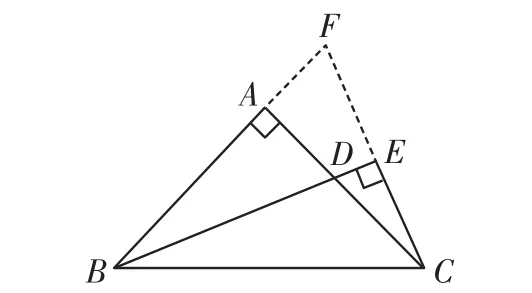
图2

分析：因为B E是∠A B C的平分线，且B E⊥C E，以B E为对称轴进行变换，点C的对称点必是B A和C E的延长线的交点F，则△B C F为等腰三角形，根据等腰三角形的性质可使问题巧妙获解.

解：因为B E是∠A B C的平分线，且B E⊥C E，以B E为对称轴进行变换，点C的对称点则为B A和C E的延长线的交点F，则△B C F为等腰三角形.

所以C E＝E F，即C F＝2 C E.

在△A B D和△A C F中，

因为∠B A D＝∠C A F＝90°，

A B＝A C，

∠A B D＝90°－∠F＝∠A C F，

所以△A B D≌△A C F（ASA），

所以B D＝C F＝2 C E.

三、图形含有线段的垂直平分线，以垂直平分线为对称轴构造等腰三角形

例3如图3，在△A B C中，A B＝ A C，∠A＝120°，A B的垂直平分线交A B于点E、交B C于点D，试说明：

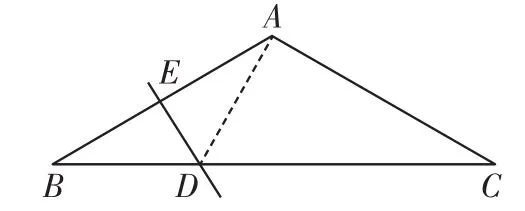
图3

分析：因为D E是线段A B的垂直平分线，以D E为对称轴进行变换，点B的对称点必为点A，连接A D，则△A B D为等腰三角形，根据等腰三角形的性质可使问题迅速获解.

解：D E为线段A B的垂直平分线，连接A D，则△A B D为等腰三角形.

因为A B＝A C，∠A＝120°，

所以∠B＝∠C＝30°.

因为△A B D为等腰三角形，

B D＝A D，则∠B A D＝∠B＝30°，

从而∠D A C＝90°.

根据图形的轴对称，巧妙构造等腰三角形，可迅速找到解题途径，不仅能使问题化难为易，迎刃而解，而且有助于培养同学们探索求新的学习习惯，提高同学们的数学思维能力和几何解题能力.