三角形角平分线的应用

□韩春见

三角形角平分线的应用

□韩春见

三角形的角平分线是三角形中的一条重要线段，要全面学好三角形的相关知识，需对三角形的角平分线给予足够的关注.

一、直接用角平分线分得的两个角相等

例1（1）如图1，点D是△A B C中∠A B C和∠A C B两个内角平分线的交点，求证：∠D＝90°＋

图1

图2

（2）如图2，点D是△A B C中∠A B C和∠A C B两个外角平分线的交点，试猜想∠D与∠A的数量关系，并证明你的结论.

（2）为结论开放问题，沿着（1）的思路：先表示∠D和∠A，再借助条件B D和C D为∠A B C和∠A C B两个外角平分线，易猜想到结论为∠D＝ 90°－

解：（1）∵点D是△A B C中∠A B C和∠A C B两个内角平分线的交点，

在△B C D中，

∠D＝180°－（∠D B C＋∠D C B），

在△A B C中，

∠A B C＋∠A C B＝180°－∠A，

证明略.

点评：（1）本题主要就是运用了角平分线分得的两个小角等于原两大角的一半.（2）本题的第2小问是结论开放问题，准确猜想出结论是解决问题的关键.

二、利用三线合一

例2已知：如图3，P是∠A O B平分线上的一点，P C⊥O A，P D⊥O B，垂足分别为C、D.求证：

（1）O C＝O D.

（2）O P是C D的垂直平分线.

图3

分析：该题涉及角平分线和线段的垂直平分线，这两者之间有较为紧密的联系.在该题中，可利用这两者之间的关系为解题创造条件.

证明：（1）由条件可知，

∠P C O＝∠P D O＝90°，

∠C O P＝∠D O P，O P＝O P，

故△P O C≌△P O D.

所以O C＝O D.

（2）由（1）知△P O C≌△P O D，

所以C P＝D P.

由定理“到一条线段两个端点距离相等的点，在这条线段的垂直平分线上”，可知点P在线段C D的垂直平分线上，

又∵O C＝O D，同理可知点O也在线段C D的垂直平分线上，

故O P是C D的垂直平分线.

引申：如图3，C、D是射线O A、O B上的两点.若O P是线段C D的垂直平分线，

求证：O P是∠A O B的角平分线.

证明：∵O P是线段C D的垂直平分线，

∴O C＝O D，

∴由等腰三角形三线合一，可知O P是∠A O B的角平分线.

点评：例2是利用O P是∠A O B的角平分线这一条件，证明O P是线段C D的垂直平分线的.引申问题却反过来用O P是线段C D的垂直平分线这一条件，来证明O P是∠A O B的角平分线.在很多情况下二者可互相转化，互为条件，这是解这类问题的关键.

三、向角的两边作垂线

例3已知：如图4，∠C＝90°，∠B＝30°，A D是Rt△A B C的角平分线.求证：B D＝2 C D.

图4

分析：根据已知条件可求出∠B A C的度数，再由A D是△A B C的角平分线，可分别求出图4中其余各角的度数，再证明结论就容易了.

证明：由∠C＝90°，∠B＝30°，知∠B A C＝60°.

∵A D是△A B C的角平分线，

∴∠B A D＝∠C A D=30°，

∴∠B＝∠B A D，∴A D＝B D.

在△A D C中，

∠D A C＝30°，∠C＝90°，

∴A D＝2 C D.故B D＝2 C D.

引申：该题中，若条件不变，如图4，从D点向A B作垂线交A B于点E，请问：（1）△A D E≌△A D C是否成立？（2）B D＝2 D C是否成立？

证明：（1）∵A D是△A B C的角平分线，

∴由角平分线的性质可知D E＝D C，

在Rt△A D E和Rt△A D C中，

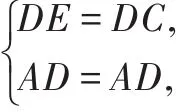
∴Rt△A D E≌Rt△A D C.

（2）在△B D E中，

∠B＝30°，∠B E D＝90°，

∴B D＝2 D E.

由（1）可知D E＝D C，故B D＝2 D C.

点评：全等的条件可轻松找到，B D＝2 D E显然也成立.这是在特殊角三角形的情况下考虑的，若推广到一般三角形的情况，解答该题的主要依据“角平分线上的点到这个角的两边的距离相等”依然是一个重要的解题条件.

例4已知：如图5，△A B C的外角∠C B D和∠B C E的平分线相交于点F.求证：点F在∠D A E的平分线上.

图5

分析：该题图比较简单，单从上图中很难看出应该怎么证明结论.但问题既然涉及角平分线，我们很容易想到定理“在一个角的内部，且到角的两边距离相等的点，在这个角的平分线上”，所以不妨过点F分别作B D、B C、C E的垂线段，这样就找到了解决问题的切入点.

证明：如图5，过点F分别作B D、B C、C E的垂线段F G、F H、F M.

∵B F是∠C B D的平分线，

∴F G＝F H.

同理F H＝F M，则F G＝F M.

∵点F在∠D A E内，且点F到A D、A E的距离相等，

∴点F在∠D A E的平分线上.

引申：该题中，若条件不变，请问：∠A与∠B F C有怎样的数量关系？（∠B F C＝90°－∠A，探索求解过程程略）.

点评：以上两题巧妙地利用了角平分线的性质和判定来证明问题.角平分线的性质和判定是平面几何中的两个重要知识点，在中考中独立命题不多，常与线段垂直平分线、三角形全等以及圆等其他几何知识相互渗透，往往以填空题、解答题等低中档题目出现.

四、在角的两边截取相等的线段

例5如图6，已知△A B C的角平分线A D交B C于点D，且∠A B C＝2∠C，A B＝4cm，B D＝3cm，求线段A C的长.

图6

分析：要求线段A C的长，就是要想办法将线段A C与已知线段A B和B D联系起来.利用∠B A D＝∠C A D相等，可在∠B A C的两边截取相等线段，如在边A B所在的射线上截取A E＝A C，可得△A E D≌△A C D，只要证明△B D E是一个等腰三角形，即可得A C＝A E＝A B＋B E＝A B＋B D＝7cm.（注：在边A C上截取也可求得A C＝7cm）.

解：延长A B到E，使A E＝A C，连接D E.

∵△A B C的角平分线A D交B C于点D，

∴∠B A D＝∠C A D.

∵A D＝A D，

∴△A D E≌△A D C，

∴∠E＝∠C.

∵∠A B C＝2∠C，

∠A B C＝∠E＋∠B D E，

∴∠E＝∠B D E，

∴B E＝B D＝3cm，

A C＝A E＝A B＋B E＝A B＋B D＝4＋3＝7（cm）.

点评：当给定的题设条件及图形并不具有明显的全等条件时，需要我们认真观察、分析，根据图形的结构特征，挖掘潜在因素，通过添加适当的辅助线，巧构全等三角形.三角形的角平分线为构造全等三角形提供了一对相等角（∠B A D＝∠C A D）和一对公共边（A D＝A D），只需再添加一个条件就可得到全等，借助全等三角形的性质，就可迅速找到解题的途径.