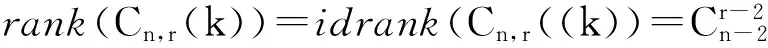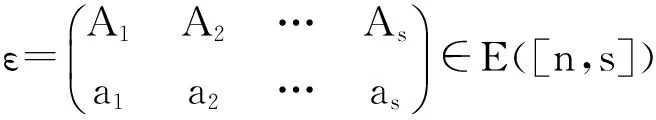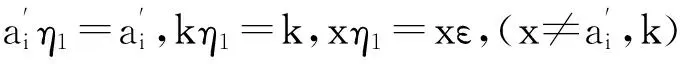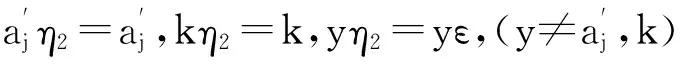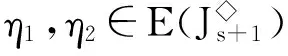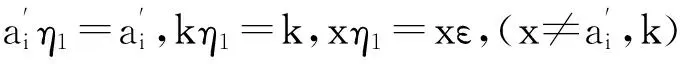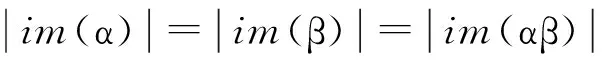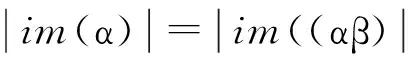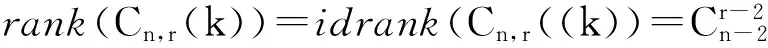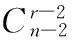半群Cn,r(k)的秩和幂等元秩
亓顺芹
(贵州师范大学 数学科学学院, 贵州 贵阳 550001)
半群Cn,r(k)的秩和幂等元秩
亓顺芹
(贵州师范大学 数学科学学院, 贵州 贵阳 550001)
变换半群;保序;降序;幂等元秩;秩
0 引言
设[n]={1,2,…,n}并赋予自然数的大小序,Singn是[n]上的奇异变换半群。设α∈Singn,若对任意的x∈[n],有xα≤x,则称α是降序的;若对任意的x,y∈[n], x≤y⟹xα≤yα,则称α是保序的。设Dn和On分别为Singn中的所有降序变换集和所有保序变换集,则Dn和On是Singn的子半群。设POn=On∪{α:dom(α)⊂[n],(∀x,y∈dom((α))x≤y⟹xα≤yα}是保序部分变换半群(不含[n]上的恒等变换),PDn=Dn∪{α:dom(α)⊂[n],(∀x,y∈dom((α))xα≤x}是降序部分变换半群(不含[n]上的恒等变换)。记Cn=Dn∩On,PCn=PDn∩POn,则Cn和PCn是POn(或PDn)的子半群,Cn和PCn分别称为降序且保序变换半群和降序且保序部分变换半群。
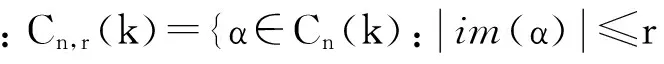
1 预备知识
对任意的α∈Cn,r(k)(r≥2),由降序性和保序性易验证α有如下表示法(称为α的标准表示):
这里:a1 为叙述方便,在Cn,r(k)上引入如下的二元关系:对任意的α,,β∈Cn,r(k),定义 αL◇β⟺im(α)=im(β) αR◇β⟺ker(α)=ker(β) 则L◇,R◇与J◇都是Cn,r(k)上的等价关系。易见L◇⊆J◇,R◇⊆J◇,对于1≤m≤r≤n-1,记 设A是[n]的子集,C是A的子集,如果C满足:x,y∈C,z∈A,且x≤z≤y⟹z∈C,则称C是A上的凸子集。 设S是Cn,r(k)的子集,通常用E(S)表示S中所有幂等元组成的集合。本文未定义的术语及符号请参见文献[10]。 定理1 设1≤r≤n-1,2≤k≤n,则 引理1 设α∈Cn,r(k),则α是幂等元的充要条件是对任意的t∈im(α),有 t=min{x:x∈tα-1}。 证明 由于α∈Cn(k)是幂等元的充要条件是对任意的t∈im(α),有t∈tα-1,故α∈Cn,r(k)是幂等元的充要条件是对任意的t∈im(α),有t=min{x:x∈tα-1}(因此由t∈tα-1且x∈tα-1可推出t=tα=xα≤x)。 证明 任取 显然kε=k。其中:1=a1 证明 任取 其中1=a1 xγ=v0,(x∈[v0,max(v0α-1)]) xγ=xα,(x∈[[n]v0,max(v0α-1)]) 则β,γ是Cn,r(k)的幂等元,于是 Aiβγ=ciγ=v0=Aiα,(x∈[v0,max(v0α-1)]) Aiβγ=ciγ=ai=Aiα,(x∈[[n]v0,max(v0α-1)]) 引理4 设α,β∈Cn,r(k),若(α,β)∈J◇,(α,αβ)∈J◇,则(αβ,β)∈L◇,(α,αβ)∈R◇。 证明 对任意的α,β∈Cn,r(k),若(α,β)∈J◇,(α,αβ)∈J◇,则 定理1的证明: [1] GOMES G M S,HOWIE J M.On the ranks of certain semigroups of order-preserving Transformations[J].Semigroup Forum,1992(45):272-282. [2] GARBA G U.On the Idempotent Ranks of Certain Semigroups of Order-Preserving ransformations[J].Portugal Math,1994,51:185-204. [3] HIGGINS P M.Idempotent Depth in Semigroups of Order-Preserving Mappings [J].Proc Roy Soc Edinburgh Sec A,1994,124(5):1045-1058. [4] LARADJI A,UMAR A.On Certain Finite Semigroups of Order-Decreasing Transformations I[J].Semigroup Forum,2004,69(2):184-200. [5] LEVI I.Nilpotent Ranks of Semigroups of Partial Transformations [J].Semigroup Forum,2006,72(3):459-476. [6] 高荣海,徐波.降序有限部分变换半群的幂等元秩[J].西南大学学报(自然科学版),2008,30(8):9-12. [7] 徐波,冯荣权,高荣海.一类变换半群的秩[J].数学的实践与认识,2010,40(8):222-224. [8] 赵平,游泰杰,徐波等.降序且保序有限部分变换半群的幂等元秩[J].山东大学学报(理学版),2011,46(4):75-77. [9] 赵平,游泰杰,徐波.半群CPOn的秩[J].西南大学学报(自然科学版),2011,33(6):106-110. [10]HOWIE J M.An Introduction to Semigroup Theory [M].London:Academic Press,1976. Rank and idempotent rank of the semigroups Cn,r(k) QI Shunqin (School of Mathematics Science,Guizhou Normal University, Guiyang, Guizhou 550001,China) transformation semigroup; order-preserving; order-decreasing; idempotent rank; rank 1004—5570(2016)05-0057-03 2016-05-25 国家自然科学基金项目(批准号11461014) 亓顺芹(1991-),女,硕士研究生,研究方向:半群理论及编码理论,E-mail:2812889092@qq.com. O152.5 A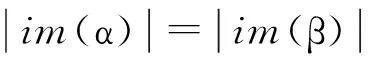
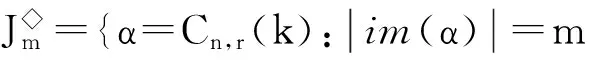
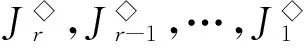
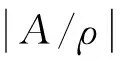
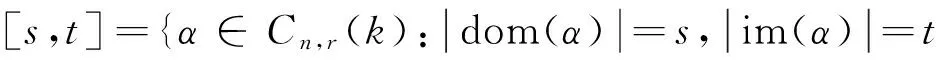

2 主要结果及其证明