全空间中一类椭圆方程组解的存在性
张虎梅,李鸿翔,郝悦斌
(山西大学 数学科学学院,山西 太原 030006)
全空间中一类椭圆方程组解的存在性
张虎梅,李鸿翔,郝悦斌
(山西大学 数学科学学院,山西 太原 030006)
讨论了下面问题:
椭圆方程组;Nehari流形;能量泛函
0 引言
研究下面一类椭圆方程组
(1)
椭圆方程组解的存在性得到了广泛的研究,涌现出很多重要的研究成果。 尤其在有界区域上出现了大量的研究工作,比如Alves在文献 [1]中研究了下面的问题
(2)

(3)

(4)
他们通过对f,g进行了适当假设证明了方程组(4)至少存在一个正解。
还有在文献 [11]中Liu对相类似的方程
(5)
也进行了研究,她先对a(x),b(x)作了合适的衰减假设,再通过临界点理论,在有界的球内找到了近似解,然后通过分析找到的近似解的结构再取极限,从而证明了方程组(5)有无穷多的正能量解。因为本文是在RN上来研究,而且要考虑比较一般的权函数q(x),这将会导致紧性严重缺失,所以需要更加仔细地分析极小化序列,研究极小化序列的各种可能行为来克服紧性缺失的问题,本文将作出适当的假设来证明椭圆方程组(1)解的存在性。现在给出q的假设:
(Q):0<δ:=infRNq 本文的结论如下: 定理1 若N≥3,α>1,β>1,α+β∈(2,2*),并且q满足假设Q,那么椭圆方程组(1)至少存在一个非平凡的非负弱解。 定义H1(RN)的内积为: (u1,u2)=∫RN▽u1·▽u2+q(x)u1·u2dx, 相对应的范数为:‖u‖={∫RN|▽u|2+q(x)u2 要在空间X上对方程组(1)进行讨论。相对应地定义能量泛函为: 方程组(1)的一个弱解就相当于泛函I(u,v)在H1(RN)×H1(RN)上的一个临界点。对泛函I(u,v)来讲,易知I无下界,所以要将I限制到Nehari流形上,定义如下: N={(u,v)∈X|u≠0,v≠0,〈I′(u,v),(u,v)〉=0} 若(u,v)∈N,则相对应的能量泛函是: 现在定义:m=inf(u,v)∈NI(u,v)。 引理1 N是非空集,m>0。 证明 首先证N是非空集。 因为(u,v)∈X,u≠0,v≠0,且∫RN|u|α|v|βdx≠0,所以存在t>0,使得(tu,tv)∈N,就有 再证m>0。因为(u,v)∈N,则可用Sobolev不等式和不等式|u|α|v|β≤|u|α+β+|v|α+β,得到 ‖u‖2+‖v‖2=2∫RN|u|α|v|βdx ≤2∫RN|u|α+β+|v|α+βdx 假定{(uk,vk)}k⊂N是I的极小化序列,而显然(|uk|,|vk|)∈N,同时又有I(|uk|,|vk|)=I(uk,vk)成立,故{(|uk|,|vk|)}k也是极小化序列,所以在RN中有uk(x)≥0,vk(x)≥0,且uk,vk在H1(RN)中是有界的,故有u,v∈H1(RN)使得 ·uk(x)→u(x)a.e.,vk(x)→v(x)a.e.x∈RN。 引理2 λ>0。 需要考虑3种情况:l=λ,l=0,和 0 引理3 若l=λ,则(u,v)∈N,I(u,v)=m。 2∫RN|uk|α|vk|βdx, 而显然有I(u,v)≥m,又通过范数的弱下半连续性可得 I(u,v)≤lim infkI(uk,vk)=m。引理3证毕。 现在我们定义一个泛函: 最后定义mγ=inf(u,v)∈NγIγ(u,v)。 引理4 存在(u,v)∈Nγ使得Iγ(u,v)=mγ。 ≤∫RN|▽ek|2+|▽fk|2dx+γ∫RN|ek|2+|fk|2dx =2∫RN|ek|α|fk|βdx =2∫RN|wk|α|zk|βdx。 =Iγ(ek,fk)。 现在来证明弱极限u,v∈Nγ且Iγ(u,v)=mγ。 先证u,v∈Nγ,由类似引理1的证明得 (6) 取极限得 0 =t2lim infkIγ(uk,vk)=t2mγ 再由范数的弱下半连续性可得 Iγ(u,v)≤lim infkIγ(uk,vk)=mγ,而Iγ(u,v)≥mγ,故有Iγ(u,v)=mγ。引理4证毕。 引理5 m 证明 易知Nγ≠Φ,mγ>0,存在(u0,v0)∈Nγ使得Iγ(u0,v0)=mγ,且u0≥0,v0≥0。由Q的假设我们可推断存在δ1>0和一个球BR(x1)使得对∀x∈BR(x1)有q(x)≤γ-δ1,而且也存在δ2>0,一个球BR(x2)以及一个集合A⊆BR(x2)使得在A中处处有u0(x)≥δ2。 现在可以定义一个函数u1∈H1(RN)使得u1(x)=u0(x-x1+x2)。如果x∈BR(x1),那么x-x1+x2∈BR(x2),因此在一个集合A′⊆BR(x1)中处处有u1(x)≥δ2。则 因为q(x)≤γ,所以 从而 因此存在t∈(0,1)使得(tu1,tv1)∈N有 引理6 u=0,v=0不会发生。 证明 可以固定ε>0,取Rε>0使得对∀|x|≥Rε有|q(x)-γ|≤ε,从而 (7) 2∫RN|uk|α|vk|βdx, 所以易知对每个k存在tk≥1使得对(tkuk,tkvk)∈Nγ有 (8) (9) (10) |uk|α|vk|βdx- 取极限得mγ≤m。矛盾。引理6证毕。 首先通过选择一个正的递增序列{Rj}j使得Rj+1>Rj+1,因此当Rj→+∞时有下列性质成立: 又因为在RN中的有界子集上存在紧性,所以对每个j有下列结论成立: 故对每个j∈Ν存在子序列{(ukj,vkj)}有 现在取{(ukj,vkj)}作为一个新的极小化序列记为{(uj,vj)}j。 考虑对每个j存在一个函数ψj∈C∞(RN)使得下列结论成立: · 对每个x有0≤ψj(x)≤1, · 若|x|≤Rj,则ψj(x)=1, · 若|x|≥Rj+1,则ψj(x)=0, · 对每个x有|▽ψj(x)|≤C。 =|ψjuj|α|ψjvj|β+(1-ψj)α|uj|α(1-ψj)β|vj|β 另一方面 ∫RN|uj|α|vj|βdx=∫BRj|uj|α|vj|βdx+ ∫RN|u″j|α|v″j|βdx ∫RNψj(1-ψj)|▽uj|2dx-∫RNψjuj▽uj·▽ψjdx -∫RNψjuj▽uj·▽ψjdx。 |∫RNψjuj▽uj·▽ψjdx|≤∫RNψjuj|▽uj||▽ψj|dx 同样的有 |∫RN(1-ψj)uj▽uj·▽ψjdx|≤ο(1), ∫RN|▽u″j|2dx+ο(1), ∫RN|▽v″j|2dx+ο(1), 引理9 若l∈(0,λ),(u,v)∈N,则I(u,v)=m。 由引理8我们可以写出 (11) 所以对于足够大的j可推出 (12) 因此,存在sj∈(0,1)使得(sju″j,sjv″j)∈Nγ有 =I(uj,vj)+ο(1), 取极限得mγ≤m。 矛盾。 故有I(u,v)≥m,所以I(u,v)=m成立。 引理9证毕。 引理10 l=0不会发生。 2∫RN|u|α|v|βdx, [1] AlVES C O,MORAIS FILHO D C,SOUTO M A S.On systems of elliptic equations involving subcritical or critical Sobolev exponents[J] .Nonlinear Analysis,2000,42:771-787. [2] BOUCHEKIF M,NASRI YASMINA.On elliptic system involving critical Sobolev-Hardy exponents[J].Mediterr J math,2008,5:237-252. [3] BOUCHEKIF M,NASRI YASMINA.On a elliptic system at resonance[J].Annali di Matematica,2010,189:227-240. [4] KANG D,PENG S.Existence and asymptotic properties of solutions to elliptic systems involving multiple critical exponents[J].Science China Mathematics,2011,54(2):243-256. [5] ZHANG Y.Multiple solutions of an inhomogeneous Neumann problem for an elliptic system with critical Sobolev exponent[J].Nonlinear Anal,2012,75:2047-2059. [6] HAN P.High-energy positive solutions for a critical growth Dirichlet problem in noncontractible domains[J].Nonlinear Anal,2005,60:369-387. [7] 张亚静,郝江浩.一个非齐次临界Neumann 问题的多正解[J].数学物理学报,2013,33A(4):661-672. [8] WU T.Multiple positive solutions for semilinear elliptic systems with nonlinear boundary condition[J].Appl Math Comput,2007,189:1712-1722. [9] BROWN K J,WU T.A semilinear elliptic system involving nonlinear boundary condition sign-changing weight function[J].J Math Anal Appl,2008,337:1326-1336. [10]LI G,WANG C.The existence of nontrivial solutions to a semilinear elliptic systems in the whole space without the Ambrosetti-Rabinowitz condition[J].Acta Mathematica Scientia,2010,30B(6):1917-1936. [11]LIU Z.Infinitely many solutions for some nonlinear scalar system of two elliptic equations[J].J Math Anal Appl,2011,382:731-747. Existence of solutions for elliptic system in the whole space ZHANG Humei,LI Hongxiang,HAO Yuebin (School of Mathematical Sciences, Shanxi University, Taiyuan,Shanxi 030006,China) By using the calculus of variations, we can prove that at least one nontrivia and nonnegative solution exists in the following elliptic system. ellipticsystem;Neharimanifold;energyfunctional 1004—5570(2016)05-0041-08 2016-04-10 国家自然科学基金资助项目(61374089);山西省自然科学基金资助项目(2014011005-2) 张虎梅(1989-),女,硕士研究生,研究方向:非线性泛函分析,E-mail:1244755406@qq.com. O175.25 A 应用变分法证明了以上椭圆方程组至少存在一个非平凡的非负解。1 预备知识


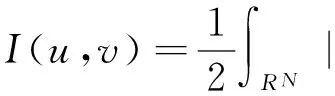



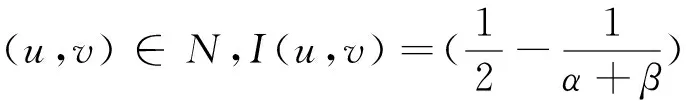
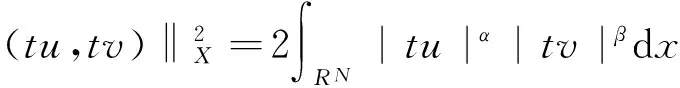





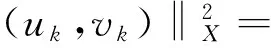


2 l与λ的3种情形
2.1 l=λ
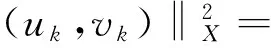
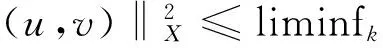
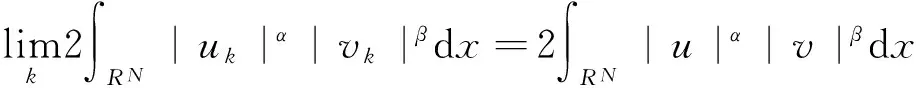



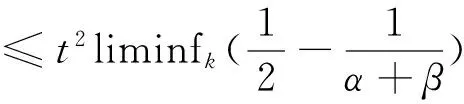
2.2 l=0且u=0,v=0




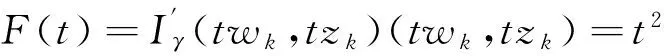



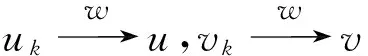




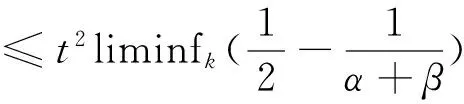












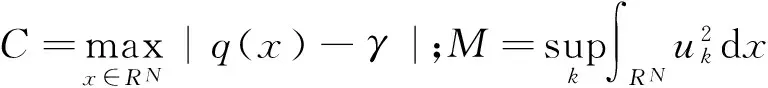




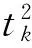
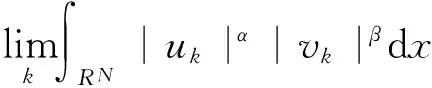
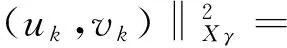

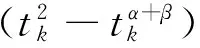

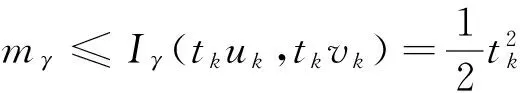

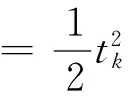

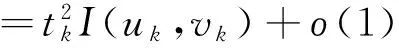
2.3 0

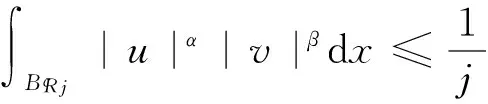




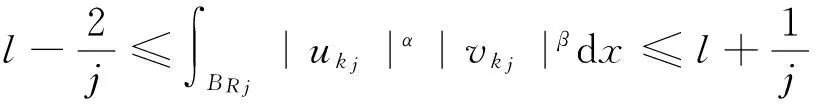






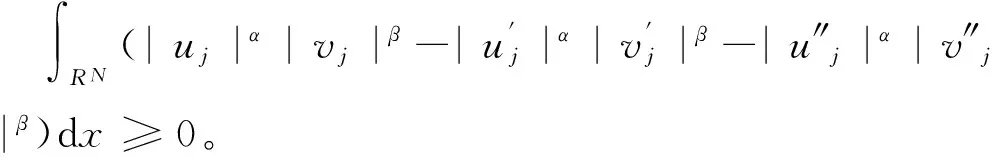



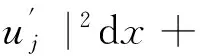
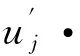
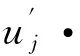




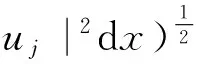
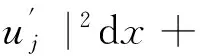


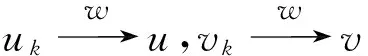

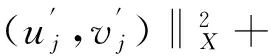









2.4 l=0

3 定理1的证明


