浅析初中数学中点问题

山西祁县第三中学　畅建芬

浅析初中数学中点问题

山西祁县第三中学畅建芬

初中数学线段中点

线段的中点是几何图形中的一个特殊点，与中点有关的问题很多。在近几年的中考题中，中点问题是高频题，涉及到选择、填空、简答每一种题型。添加适当的辅助线，恰当地利用中点是处理中点问题的关键。

一、等腰三角形的“三线合一”

如果已知等腰三角形底边上的中点，就要联想到“三线合一”的性质。

例如：如图，已知：∠BAC=60°，AB= AC=2，D为BC边的中点，则AD=____

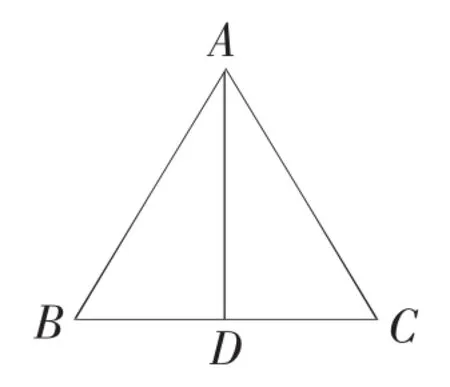
分析：知道了底边BC的中点D，应该联想到“三线合一”，连接AD，则AD既是底边的中线又是底边的高线还是顶角的角平分线，再利用直角三角形的锐角三角函数或勾股定理都可以解决问题。

二、直角三角形斜边上的中线等于斜边的一半

如果已知中有垂直或直角，就要看中点是否是直角三角形斜边上的中点，用“直角三角形斜边上的中线等于斜边的一半”这一定理来解决问题。

例如：如图，已知△ABC中，BD、CE为高线，点M是DE的中点，点N是BC的中点.求证：MN⊥DE.

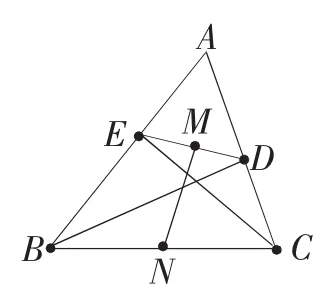
分析：本题是从另一类重要的特殊图形——直角三角形入手，揭示中点问题的解法。由于直角三角形斜边上的中线等于斜边的一半。因此如果题目中有直角三角形斜边中点的条件，那么最好的辅助线是做出斜边中线，这样就能得到两个腰长相等的等腰三角形，把直角三角形问题转化为等腰三角形问题，从而实现直角三角形与等腰三角形的互化，可以获得更多的条件，为解题提供思路。

三、三角形的中位线

如果条件告诉的中点既不是直角三角形斜边的中点，也不是等腰三角形底边的中点，可联想三角形的中位线定理。

例如：如图，△ABC中，中线BE、CD相交于 F，求证：FC=2FD.

分析：由已知三角形两边的中点，想到连接两中点构成中位线，运用中位线定理解决问题。

四、遇到两平行线所截得的线段的中点时，常联想“八字型”全等三角形

例如：如图：梯形 ABCD中，∠A=90°，AD∥BC，AD=1，BC=2，CD=3，E为AB中点，求证：DE⊥EC。

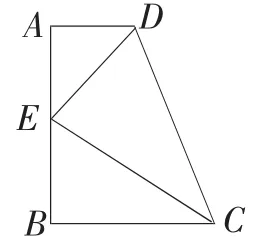
分析：如果直接证明，是不容易的，联想到AD∥BC，点E是AB的中点，我们延长DE，与CB的延长线交于点F，这样，我们不但构造出一对八字型的全等三角形，还得到了一个等腰三角形，从而利用等腰三角形的“三线合一”解决问题。

五、遇到中点，倍长中线构造全等

例如：如图，已知ΔABC中，AB=5，AC=3，BC上的中线AD=2，求BC的长.

分析：AD为BC边上的中线，延长AD到E，使DE=AD，连接BE，这样就构造了全等而且利用勾股定理的逆定理得到了一个直角三角形，再利用直角三角形的勾股定理得以解决。

六、中线平分三角形的面积

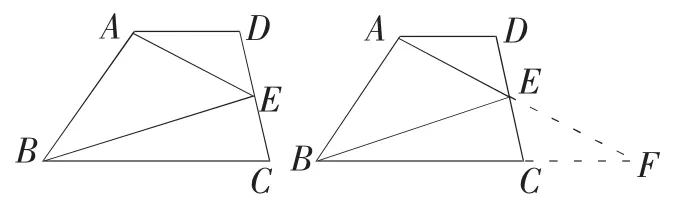
例如：如下图（左）所示，已知梯形ABCD中，AD∥BC，点E是CD的中点，连接AE、BE。求证

分析：如果直接证明，是不容易，我们就构造出一对八字型的全等三角形，如下图（右），就把三角形ADE迁移到三角形ECF的位置上，问题就好解决了。

七、垂径定理

例如：如下图所示，AB是⊙O的弦，点是AB的中点，若 AB=8cm，OC=3cm，则⊙O的半径为______cm．

分析：由点C是AB的中点，想到圆的垂径定理，得到OC⊥AB，这样就可以利用直角三角形的勾股定理来解决问题。

八、在解决几何图形问题时，我们对一些典型问题要掌握一些常用的解题方法

有些题目综合性比较强，但万变不离其宗，我们只要能从复杂的图形中分解出基本图形，仍然可以利用中点问题的一般方法来应对。

例如1、已知AD是△ABC的角平分线，AB＝10，AC＝6，CN⊥AD于N，且M是BC的中点.则MN的长为______.

分析：已知AD是角平分线，CN⊥AD，可以想到AN具有角平分线和高线两种角色，这种情况只有在等腰三角形中才有，所以延长CN与AB相交就会得到一个等腰三角形，再根据等腰三角形的三线合一的性质得到N为中点，再由三角形中位线定理得出结果。

2.如上图（右），已知△ABC中，AD是高，CE是中线，DC=BE，DG⊥CE，G为垂足.求证：G是CE的中点。

分析：要证明G为CE的中点，而已知DG⊥CE，只要证明△CDE是等腰三角形，从而得到辅助线，连接DE去证明DE=DC,而DC=BE，从而利用直角三角形斜边上的中线等于斜边的一半得以证明。

往往一道数学题并不是单一的一个知识点的应用，而是多种知识的综合，所以在处理中点问题时，要培养学生的观察能力，提高学生的图形结合能力，综合分析能力与概括能力，实现各知识间的互相转换。

总之，中点问题的种类还很多，需要我们进一步去研究探索。