夹紧顺序、夹具布局和夹紧力对装夹变形影响与同步优化分析研究

许晓宇， 赵晓慈

(北京航空航天大学机械工程及自动化学院，北京 100191)

夹紧顺序、夹具布局和夹紧力对装夹变形影响与同步优化分析研究

许晓宇， 赵晓慈

(北京航空航天大学机械工程及自动化学院，北京 100191)

为减小工件装夹变形，提高薄壁件加工精度，以薄壁零件装夹变形最小化为目标函数，通过遗传算法和有限元方法相结合，提出夹紧顺序、装夹布局和夹紧力同步分析方法。用该方法对一航空薄壁零件装夹进行优化分析，优化结果与经验设计及传统分析结果进行对比，有效地降低了工件因装夹不当引起的变形，验证了夹紧顺序、夹具布局和夹紧力同步优化方法的有效性。

装夹变形；遗传算法；有限元；同步优化

薄壁零件由于重量轻、比强度高等结构特点，在航空航天和兵器等行业有着许多重要应用。但由于其刚度较低，在装夹和加工过程中容易发生装夹变形，影响装夹变形的主要因素有夹具布局、夹紧顺序和夹紧力大小。因此，如何对薄壁零件装夹方案进行优化，从而得到多因素条件下最小装夹变形的优化模型，对薄壁件的加工具有重要工程应用价值。国内外文献对装夹优化问题有一定的研究，Prabhaharan等[1]分别通过遗传算法和蚁群算法对夹具布局进行了优化；Li等[2]利用遗传算法对一薄板件进行分析，研究支撑元件位置对工件变形的影响；Kang等[3]通过建立夹具系统三维稳定性模型，对夹紧力大小进行优化分析；Chen等[4-5]通过遗传算法和有限元方法相结合，建立夹具布局和变夹紧力分层优化模型；倪丽君[6]采用合适的接触模型，建立了参数化的工件-夹具系统有限元求解模型，研究了以最小化工件最大加工变形为目标函数的单目标装夹优化方法；周小兵[7]对装夹方案中的装夹位置进行了优化，并求解出了典型零件在典型装夹方案下的变夹紧力相关曲线；李国栋等[8]针对弱刚度工件装夹变形问题，提出了基于遗传算法的夹具布局和夹紧顺序同步优化方法；张传泰[9]基于定位原理的数学模型，提出工件装夹稳定性的判断准则；周孝伦等[10]基于对接触问题的处理和遗传算法，提出了夹具布局和夹紧力的同步优化方法。由于加工变形与装夹顺序、夹紧力、摩擦力、装夹布局和切削力等多重因素有关，以往研究大多针对其中的一、两种因素进行优化分析，忽略了各因素之间的耦合关系，并且存在异步优化问题，为此，利用遗传算法和有限元批处理技术进行求解，本文对夹紧顺序、夹紧布局及夹紧力进行同步优化，进而获得最小装夹变形的分析方法。

1　装夹方案的数学建模

1.1夹紧顺序模型

夹具在设计过程中经常使用多重夹紧元件和定位元件，假设工件装夹布局方案由m个定位元件以及n个夹紧元件构成，接触力模型如图1所示。工件受到重力旋量 Wg和法向上的夹紧力Fi=[Fiσ,0,0]的共同作用，将工件与夹具之间近似为点接触，故可设定第i个定位元件或夹紧元件的接触位置为，iσ、iτ、iβ分别为工件在第 i个接触位置正交的单位法向量和两个单位切向量。令，其中k=σ,τ,β，，为夹具布局矩阵。

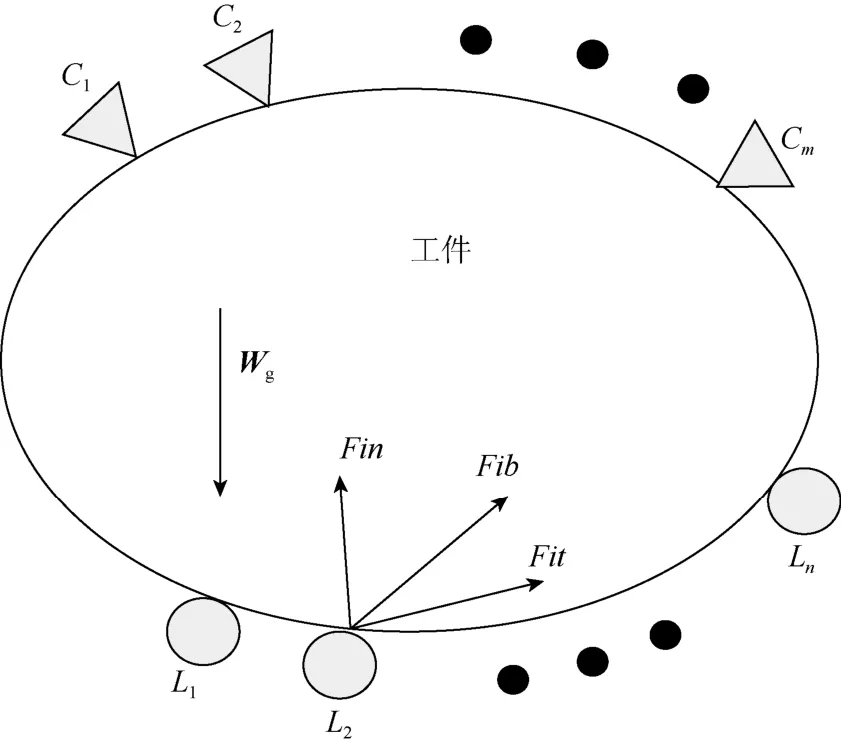
图1　装夹元件接触力模型

在工件实际定位和加工过程中，各个元件对于工件的影响并不完全相同，在初始状态，m个定位元件并不参与夹紧作用，故作用力只有工件重力和定位件支撑力，工件的静力平衡方程可表示为：

夹紧元件C1对工件施加夹紧力Fc1，则此时静力平衡方程可以表示为：

其中，Gp1为夹紧步骤1中前m个定位件结构矩阵，Gc1为夹紧元件C1矩阵。

由此递推，加紧步骤j中的平衡方程为：

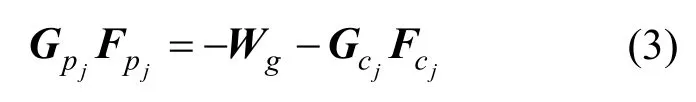
1.2约束条件

1.2.1摩擦锥约束条件

根据库伦摩擦定理，工件与夹具元件接触处最大的摩擦力不能大于摩擦锥，故在第q个夹紧步骤中第i个元件与工件接触处，约束条件为：

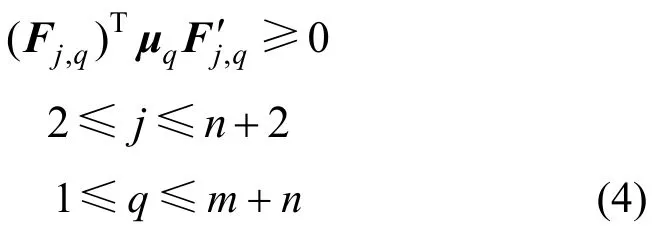
1.2.2夹紧约束

为了使工件固定，确保定位的准确性，夹紧力的方向必须指向工件且工件与装夹元件始终保持接触状态。夹紧力Fj,q与工件夹紧面的外法线矢量的点乘必须小于零，即：

1.3目标函数

针对装夹变形问题，以最大装夹变形最小化为目标函数，具有n种夹具布局，m种夹紧顺序的夹具优化模型可以描述为：

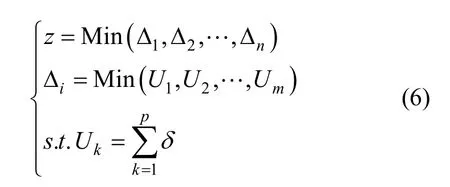
其中，z表示在夹紧力范围内，n种夹具布局m种夹紧顺序的夹紧方案中的最优夹紧方案所对应的夹紧误差，Δi表示在第i种夹具布局时，m种夹紧顺序中的最优夹紧顺序方案所对应的夹紧误差。Uk表示在第k种夹紧顺序方案的第p个夹紧步骤所对应的工件最大变形面上节点的最大位移 δ，表示节点的位移增量。

2　模型优化方法

遗传算法不关注设计变量同目标函数之间的函数关系，适合求解没有显式函数且多态的夹具布局和夹紧力优化问题。将遗传算法和有限元方法结合起来应用于夹具设计，综合考虑了夹紧顺序、夹具布局和夹紧力对工件装夹变形的影响，从而建立更为合理的装夹优化模型。通过Isight仿真软件优化组件搜索优化方向，利用有限元软件ANSYS的APDL语言建立批处理程序来计算在不同装夹方案下工件变形量。具体优化流程如图2所示，操作步骤如下：

(1) 建立有限元模型。通过有限元软件ANSYS建立APDL参数化模型作为输入文件，并设置输出结果保存文件；

(2) 建立ANSYS批处理文件。作为ANSYS与Isight命令接口；

(3) 命令集成。将 ANSYS参数化模型作为输入文件，结果文件作为输出文件，并设置输入、输出文件参数，有限元批处理文件作为中间命令，在Isight内进行组件集成；

(4) 优化操作。通过 Isight优化组件，设置遗传算法参数，定义设置变量，选择目标值和设定各变量约束条件；

(5) 运行程序。通过遗传算法对模型参数赋值，利用有限元求解适应度值并返回遗传算法操作，反复迭代并根据迭代次数判断是否可以终止优化，由此得到最优的夹具设计方案。

3　算例分析

采用上述方法对某一航空薄壁框类零件进行优化分析。该零件尺寸长120 mm，宽60 mm，高30 mm，壁厚4 mm。工件材料为7075-T6铝合金，弹性模量70 GPa，泊松比为0.3[6]。装夹模型如图3所示，其中L1、L2、L3分别为定位元件，C1、C2、C3为夹紧元件。针对3-2-1定位原则共有9种装夹顺序，如表1所示。各夹具元件的坐标取值范围如表2所示。

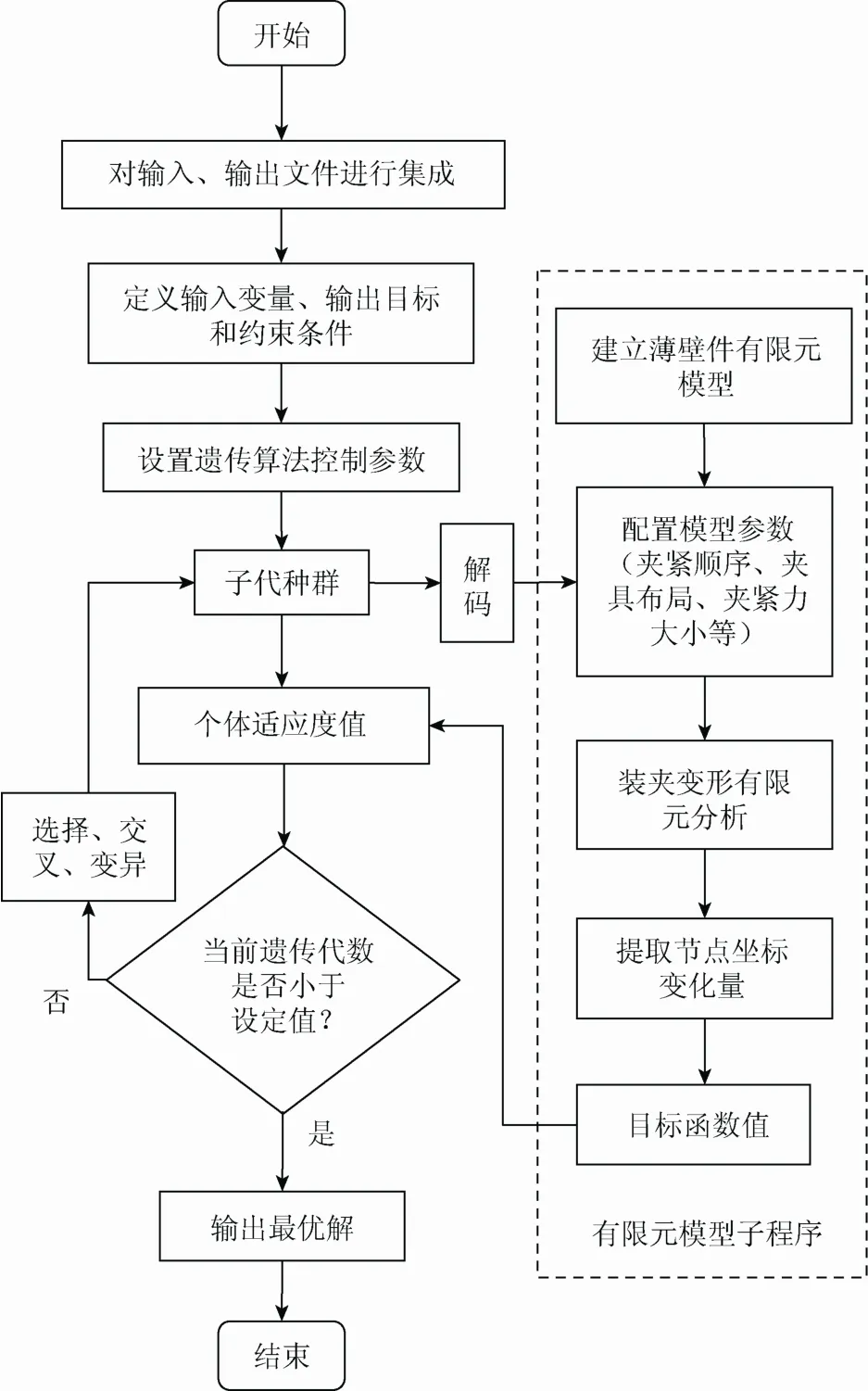
图2　同步优化流程

图3　装夹布局模型

根据装夹方案的数学模型，当不考虑工件与夹具间的摩擦时，工件在第i个夹紧步骤无摩擦稳定的充分必要条件是，式中G（i）为夹具元件的布局矩阵，F（i）为第i个接触点处的接触力向量，为接触力悬量。对符合六点定位原则的稳定性模型进行数学求解，得到无摩擦工件装夹稳定性分析的数学模型，即当且仅当满足方程有解时，工件稳定，其中B为无摩擦约束条件下的线性约束矩阵，Y为外力旋量，由此判断夹紧力是否满足夹具系统稳定性要求，本算例中各夹具元件夹紧力范围如表3所示。

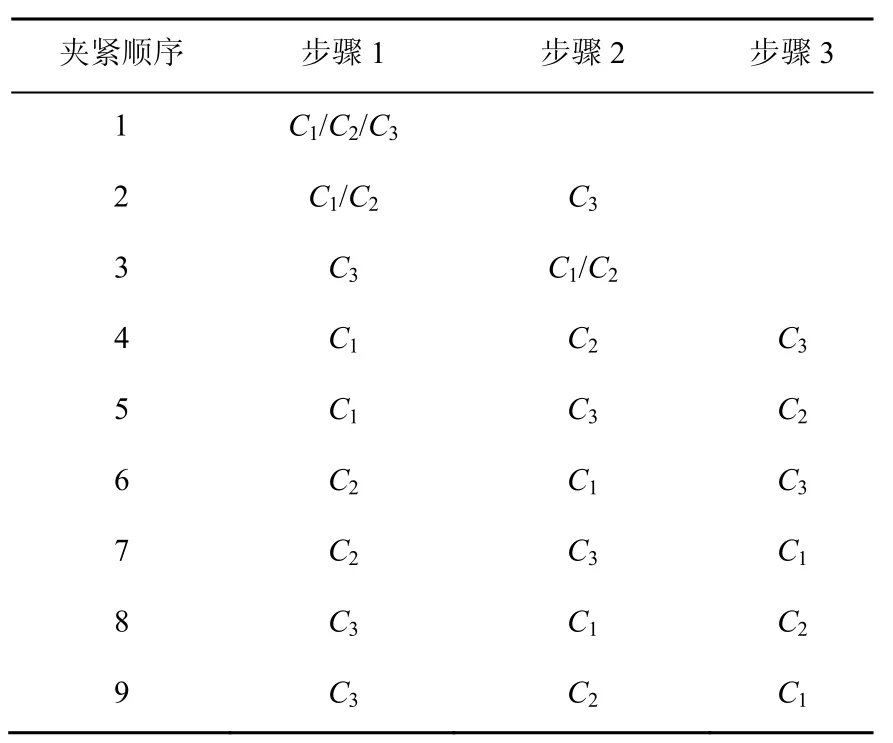
表1　夹紧顺序方案[8]

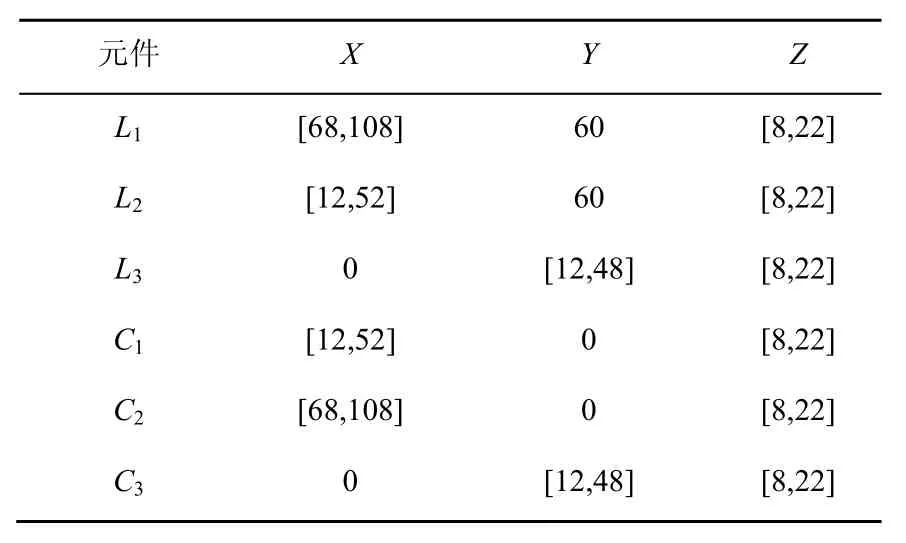
表2　夹具元件位置坐标范围[8](mm)

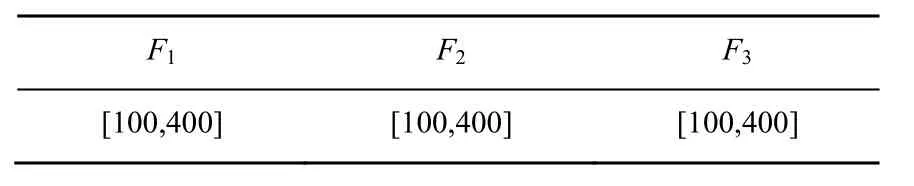
表3　夹紧力的取值范围(N)

基本遗传算法中有4个运行参数需要预先设定，M为群体大小，一般取20～100；T为中止进化代数，一般取100～500；Pc为交叉概率，一般取0.40～0.99；Pm为变异概率，一般取0.000 1～0.100 0[11]。文献[6]中，M取20，迭代次数T取100，Pc交叉概率为0.8，变异概率Pm取0.1，终止条件为最佳适应度不变的代数达到20。

通过同步优化分析，最后得到针对该框类薄壁零件在给定尺寸和材料模型条件下，最优的夹紧顺序为方案9，夹具布局和夹紧力的大小收敛情况如图4所示。图4(a)显示了遗传算法进化过程，直观地显示了每个个体所对应的目标函数值以及整体进化趋势；图4(b)显示了在进化过程中，筛选最佳适应度值的过程。从图中可以看出，随着遗传优化的不断进行，该薄壁工件最大装夹变形量不断降低，当进化代数达到设置值时，迭代终止，得到在给定参数下该优化模型的最优解。

为保证工件定位准确，加工过程中不发生位置偏移，经验设计往往采用对称分布，并施加较大的夹紧力，但增加了工件装夹变形。在异步优化中，需控制其他因素不变，只对某一变量进行优化，并保持该变量不变，优化其他变量，从而得到最优解，却忽略了各因素之间的耦合关系。将本算例优化结果与经验设计及传统异步优化分析结果进行比较，装夹变形量结果对比如表4所示。

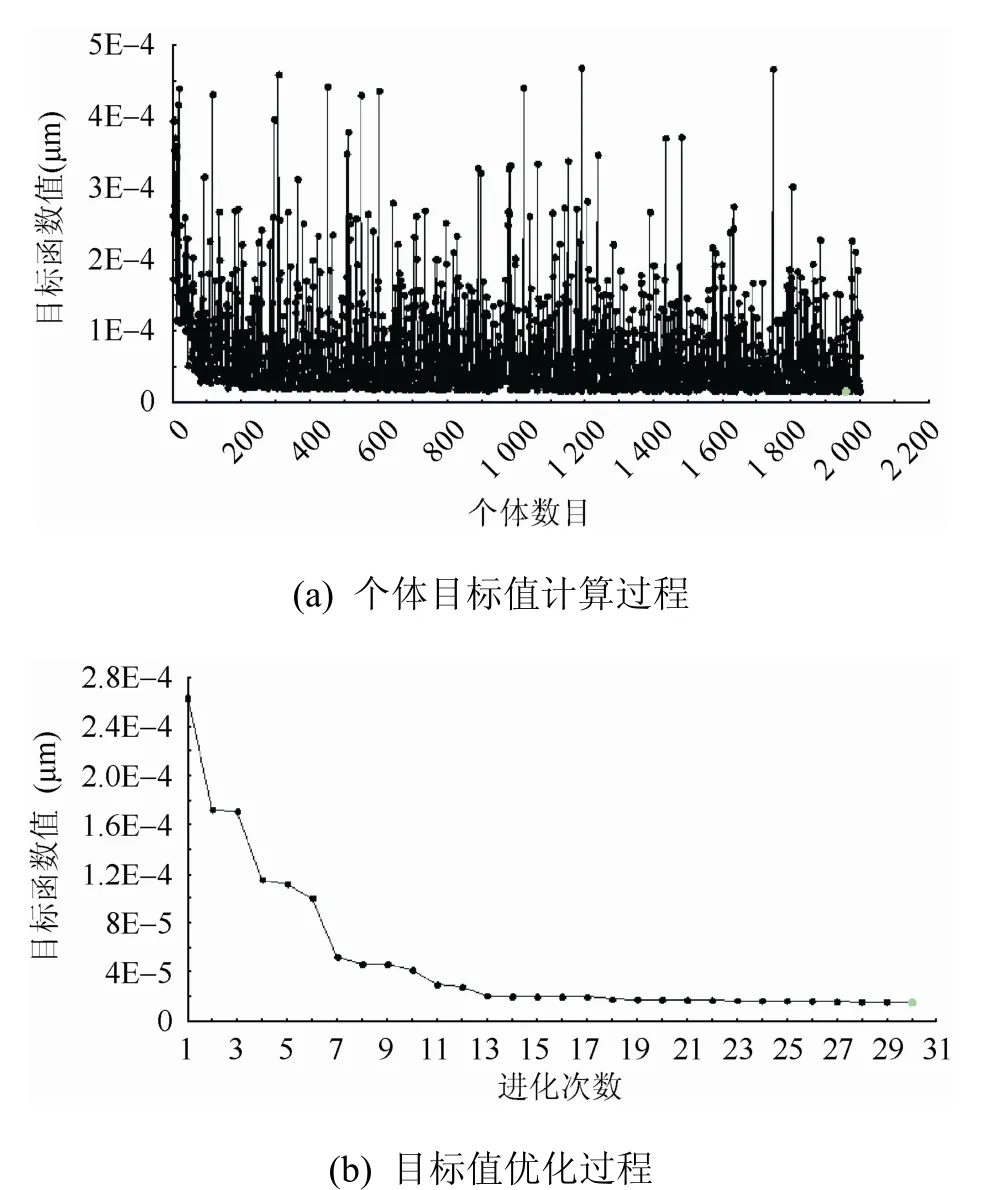
图4　遗传算法优化过程

通过同步优化分析，得到最优解的值为15.33 µm，经验设计中节点的最大变形量为109.60 µm，单目标优化最大变形量为24.84 µm，相比较经验设计和单目标优化，同步优化设计的装夹变形量分别降低了86.2%和38.3%。

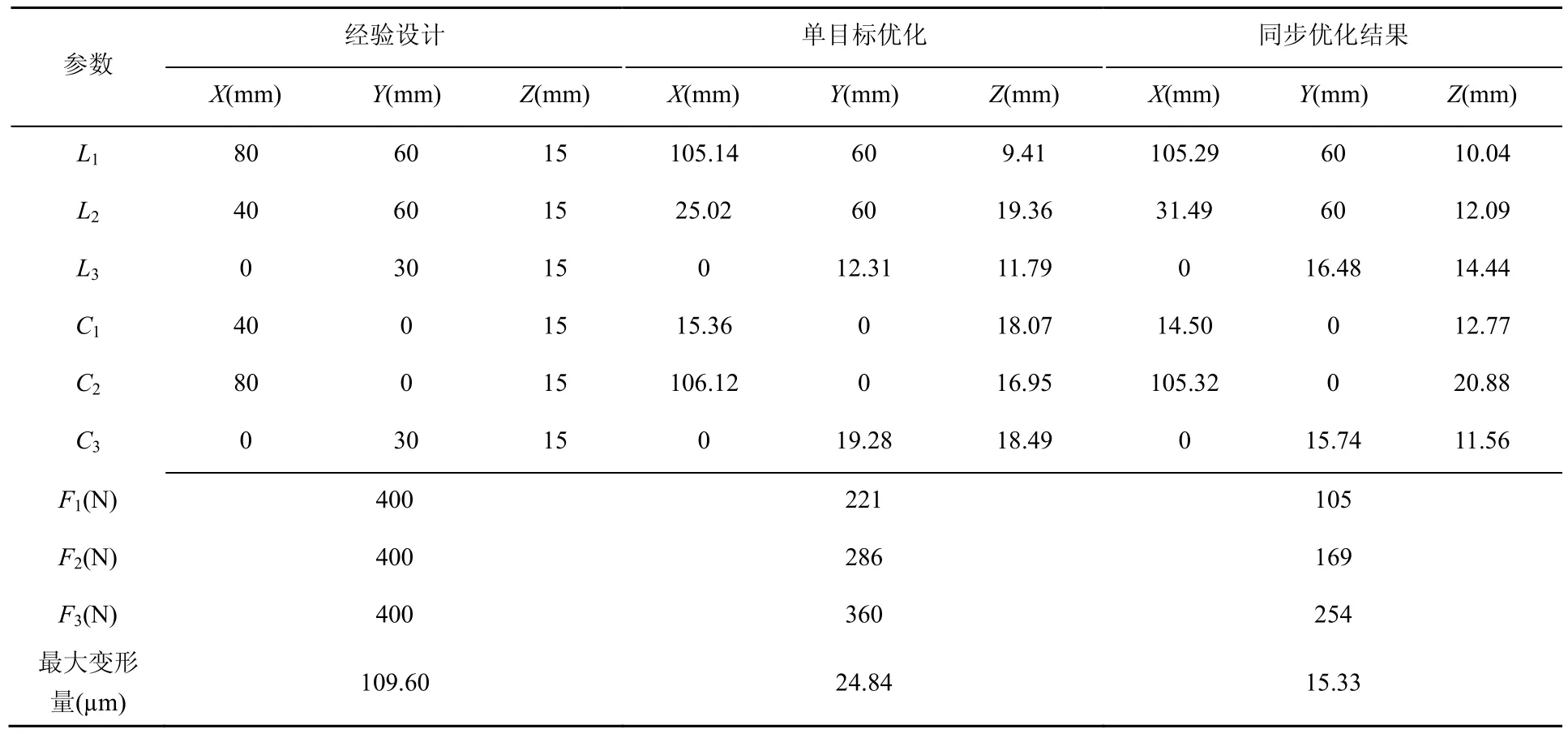
表4　经验设计、单目标优化、同步优化装夹变形量对比

4　结　论

本文针对夹具设计中的装夹变形问题，提出了夹紧顺序、夹具布局和夹紧力同步优化分析方法，减少了因夹紧顺序不同以及布局不合理、夹紧力大小设置不当而引起的工件弹性变形。利用本文提出的优化方法，对实际工程中的薄壁框类零件进行分析验证，并与经验设计和传统夹具异步优化进行比较，结果表明，夹紧顺序、夹具布局和夹紧力同步优化方法能更有效地降低装夹变形，验证了该优化方法的有效性。本文提出的同步优化模型方法，为工程中多目标优化和减少装夹变形问题提供参考。但由于夹具设计的多样性和复杂性[12]，对不同零件模型和装夹方案还有待于更全面、更深入地分析。

[1] Prabhaharan G, Padmanaban K P, Krishnakumar R. Machining fixture layout optimization using FEM and evolutionary techniques [J]. International Journal Advanced Manufacturing Technology, 2007, 32(11): 1090-1103.

[2] Li X, Molfino R, Zoppi M. Fixture layout optimization for flexible aerospace parts based on self-reconfigurable swarm intelligent fixture system [J]. International Journal of Machine Tools & Manufacture, 2013, 66(9): 1305-1313.

[3] Kang Y, Rong Y, Yang J C. Computer-aided fixture design verification. Part 3. stability analysis [J]. International Journal Advanced Manufacturing Technology, 2003, 21: 842-849.

[4] Chen W F, Ni L J, Xue J B. Deformation control through fixture layout design and clamping force optimization [J]. International Journal Advanced Manufacturing Technology, 2008, 38(9): 860-867.

[5] 陈蔚芳, 陈华, 倪丽君. 基于GA和FEM的夹具布局和变夹紧力优化设计[J]. 数值计算与计算机应用, 2009, 30(1): 1-9.

[6] 倪丽君. 计算机辅助夹具设计中的装夹优化技术[D].南京: 南京航空航天大学, 2007.

[7] 周小兵. 精密薄壁零件装夹变形的分析与控制研究[D].南京: 南京航空航天大学, 2006.

[8] 李国栋, 王海全, 李春, 等. 弱刚度工件夹紧顺序与夹具布局的同步优化[J]. 工程与试验, 2009, 49(2): 49-53.

[9] 张传泰. 基于遗传算法和有限元的工件装夹优化研究[D]. 大连: 大连理工大学, 2010.

[10] 周孝伦, 张卫红, 秦国华, 等. 基于遗传算法的夹具布局和夹紧力同步优化[J]. 机械科学与技术, 2005, 24(3): 339-342.

[11] 雷英杰, 张善文, 李续武, 等. 遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2014: 16.

[12] 沈晓红, 刘璇, 周细文, 等. 概念设计中的夹具几何特征识别[J]. 工程图学学报, 2001, 22(1): 19-25.

Clamping Sequence, Fixture Layout and Clamping Force on Machining Deformation and Synchronous Optimization Analysis

Xu Xiaoyu,Zhao Xiaoci

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

In order to minimize the clamping deformation and improve the machining accuracy of thin-walled parts, a synchronous optimization method of clamping sequences, fixture layout and clamping forces was presented with the objective function of minimizing the deformation and through the combination of genetic algorithm and finite element method. An aviation thin-walled work piece was optimized by this method, and compared the optimization results with the experience empirical design and the traditional analysis results. This method can effectively reduce the work piece deformation due to improper clamping and improve the machining accuracy. The result proved the veracity of the synchronous optimization method of clamping sequences, fixture layout and clamping forces.

clamping deformationl; genetic algorithm; finite element; synchronous optimization

TP 391

10.11996/JG.j.2095-302X.2016010020

A

2095-302X(2016)01-0020-05

2015-06-26；定稿日期：2015-08-13

许晓宇(1991–)，男，黑龙江哈尔滨人，硕士研究生。主要研究方向为CAD/CAE/CAM。E-mail：xuxiaoyu277@buaa.edu.cn

赵晓慈(1979–)，女，江苏大丰人，实验师，博士。主要研究方向为计算机辅助设计、分析及虚拟仿真等。E-mail：skyzh@buaa.edu.cn