基于Cosserat弹性杆理论的柔性线缆物理建模方法
林海立, 刘检华, 唐承统, 刘佳顺
(北京理工大学机械与车辆学院,北京 100081)
基于Cosserat弹性杆理论的柔性线缆物理建模方法
林海立, 刘检华, 唐承统, 刘佳顺
(北京理工大学机械与车辆学院,北京 100081)
针对虚拟环境中线缆敷设过程仿真的线缆建模问题,提出一种基于Cosserat弹性杆理论的柔性线缆物理建模方法。该方法在线缆离散模型的基础上根据Cosserat弹性杆理论导出线缆的总体势能,并通过优化算法得到线缆总体势能最小时的线缆形态,即线缆的平衡状态。模型考虑到线缆的柔性和连续性,能够模拟线缆的弯曲和扭转变形;通过对线缆进行离散表达,实现了对线缆总体势能的数值求解;引入罚函数将求解线缆总体势能最小值问题转化为非线性无约束优化问题;非线性无约束优化问题的求解采用信赖域方法,提高了求解的稳定性。设计并开发了虚拟环境中的线缆敷设过程仿真原型系统,并进行实例验证,证明该方法的可行性。
线缆;物理建模;敷设仿真;Cosserat弹性杆理论;能量最小
作为能量和信号的传输通道,线缆在机电产品中应用广泛,而线缆的布局和敷设安装质量直接影响机电产品的质量及可靠性。近年来,随着CAD技术的发展,在虚拟环境中进行线缆布局设计与敷设过程仿真逐渐成为国内外的研究热点。
在工程应用中,线缆具有复杂的拓扑结构,涵盖了大量的几何拓扑信息、工程语义信息和分散的布线信息[1]。柔性线缆的模型表达是进行虚拟环境下线缆敷设过程仿真的基础,该模型不仅要支持电缆的几何和拓扑特性,还要支持线缆的物理特性表达,并满足虚拟现实系统特有的实时性要求。与布料和人体组织等柔性体不同,线缆最大的特点是其长度通常远大于直径,工程中通常以线缆的中心线为扫描路径,以一定的截面信息扫描来形成线缆的三维模型,因此中心线的确定是线缆建模的关键,先前表示线缆的中心线的方法包括折线段,或自由曲线如贝塞尔曲线、B样条曲线[2-3]等,但这些方法属于线缆的几何建模,没有考虑线缆的物理属性,进行线缆敷设过程仿真时缺乏真实性。
柔性物体建模与仿真研究一直受到国内外学者的关注,IEEE(computer graphics and applications) 与SIGGRAPH曾数次召开专门的小组讨论会对该方向进行探讨[4]。由于柔性物体的形状不像刚体那样固定不变,而是随着外界条件的不同发生改变,因此建模难度很大。线缆物理建模是典型的柔性体的物理建模,由于线缆敷设过程中,其整体的运动与机器人机械臂的运动具有相似性,基于该思想,魏发远等[5]提出了一种基于蛇形机器人的线缆建模与敷设仿真方法,将来源于机器人理论的逆运动学方法应用于线缆建模中。德国学者Hergenröther 和Dähne[6]开发的虚拟装配系统中采用了类似的模型,通过一系列相连接的刚性杆表示线缆,每个连接处称为关节,在关节处加入扭簧和质点以考虑抗弯刚度和重力这两个物理属性,当线缆端部移动到某一位置时,采用能量优化法和逆运动学方法,求解出每一关节所应有的变量并使系统具有最小能量。以上建模方法能够体现线缆在敷设仿真过程中“长度不变”的性质,但考虑的线缆物理参数较少,真实性不足。
能量曲线方法由加拿大学者 Terzopoulos和Qin[7]提出,其认为曲线具有质量和抗弯特性,在一定的约束下,当曲线具有最小物理变形能时曲线处于稳定状态,因此通过数学规划或优化方法得到具有最小物理变形能的曲线,将该曲线作为线缆的中心线,即可得到处于稳定状态的线缆。王志斌等[8]在线缆布局设计中利用该模型对线缆的长度进行取样,解决了线缆取样长度不精确的问题。
弹簧质点模型[9-11]在线缆建模与敷设仿真中有较多应用,该模型具有易于实施、计算效率高的优点。在该方法中线缆由一系列质点和连接质点的直线弹簧表示,在质点处加入扭簧或者在两个质点间隔加入直线弹簧,可以考虑线缆的抗弯刚度。在弹簧质点模型解算方面,Loock等[12]在Baraff基础上采用隐式计算,该算法允许较长的时间步,具有较强的实时性,但真实性无法保证。
由于逆运动学、能量曲线和弹簧质点模型在处理线缆受约束形变时部分考虑了线缆的物理属性,具有一定真实性且具有实时性强的特点,是目前线缆敷设仿真中主要采用的物理模型。但以上建模方法考虑线缆物理属性并不全面,其中最重要的是不能对线缆的扭转变形进行模拟,使得在线缆敷设过程仿真中其真实性并不十分理想。
线缆在敷设过程中的局部应变很小,基本保持在材料的弹性范围内,因此有学者将其本构关系抽象为弹性关系,并用弹性杆模型进行线缆物理建模。弹性细杆静力学理论是Kirchhoff于1859年建立的,工程中绳索、钻杆、纤维等都曾将弹性细杆作为其力学模型[13]。刘检华等[14]提出的以Kirchhoff弹性细杆非线性力学理论为基础的虚拟环境下活动线缆建模与运动仿真方法,对活动线缆的仿真有较好的效果,但该方法需求解微分方程组的边界值,并利用“打靶法”在已知两端位置和朝向的基础上对线缆的整体外形进行求解,其问题是求解所需要的初值难以给定,而且求解时间较长,无法满足线缆敷设过程仿真的实时性需求。在物理模型求解方面,Bertails等[15]利用离散方法求解Kirchhoff方程,并提出一种离散和连续相结合的模型,将发丝模拟为一系列相连的螺旋曲线段,由通用坐标描述线缆,并用积分的方法重构线缆,从而消除了加入长度不变约束产生的硬度,提高了数值求解的稳定性,该方法为目前较为先进的弹性杆建模方法。而 Bergou等[16]采用离散微分几何的方法,显示以最少自由度的简化坐标方程表示线缆的中心线,并以标量表达线缆材料框架,以避免使用联系中心线和材料框架的硬化约束。
Cosserat理论作为Kirechhoff理论的改进,考虑了弹性杆的轴向线应变和弯曲剪应变等物理参数,建立更精确的平衡方程。Cosserat理论由Cosserat兄弟于19世纪提出,目前该方法已经成为非线性弹性力学的基本方法。Cosserat理论首先由 Pai[17]用于弹性杆这类细长的可变形结构的建模,该方法同样需通过“打靶法”数值求解微分方程得到杆的静态外形;由于数值解法在初始条件上难以确定,同时在处理自接触和与其他物体接触的问题上也存在困难,之后的方法多关注于模型的离散表达。Spillmann和Teschner[18]提出用于柔性杆动力学模型,该模型以Cosserat理论为基础导出杆件的连续能量表达式,通过对杆的离散计算出杆的每个单元具有的能量,进而由拉格朗日方程得到杆的动力学微分方程,数值求解该微分方程得到杆的动态变化。由于动力学模型需要较长时间进入稳定状态,黄劲等[19]提出了一个稳定、快速的优化策略对线缆进行形变模拟,并着重研究了大步长、准静态模拟过程中的接触处理这一关键问题。Grégoire 和 Schömer[20]提出了通用弹簧质点模型表达线缆这类柔性零件的外形,并以Cosserat理论对其弯曲和扭转进行建模,通过能量最小化过程求解线缆的平衡状态,此方法避免了动力学模型中的振动现象,具有较好的稳定性。但该方法采用比例积分控制实现模型的定长约束,引入了约束力变量,并通过迭代的方法确定约束力,使得模型变得复杂,降低了求解效率;四元数标准化约束中,为了避免线缆外形出现“V”形的异常形变,需改变了约束表达式,将四元数的模变为其倒数,这使得雅克比矩阵变得复杂,降低了求解效率;在优化问题求解中级联使用了多种优化方法以保证算法收敛,但初值的选择仍对求解效率和算法收敛性影响较大。
本文基于以上研究,提出采用Cosserat弹性杆理论对线缆进行物理建模,考虑敷设仿真中线缆做低速运动,提出了线缆的运动过程仿真可通过每一时刻线缆的静力学平衡状态进行表达,线缆的静力学平衡状态即为线缆具有最小弹性势能状态。可由Cosserat理论推导出线缆的弹性势能,通过选取适当的罚因子系数将约束转化为罚函数,并通过信赖域方法求解非线性优化问题得到线缆具有最小能量的形态。由于Cosserat弹性杆模型考虑到了弹性杆的弯曲变形,并通过四元数表示线缆截面的扭转变形(相对于基于 Kirchhoff弹性杆理论的线缆建模方法,考虑了更多物理特性),因而本文提出的方法更为精确,能够在线缆敷设过程的仿真中更加真实地表现出线缆的形态。
1 Cosserat弹性杆模型
线缆是细长的柔性体,实际敷设过程中其应变很小,可以认为其本构关系为弹性关系。因此采用Cosserat弹性杆理论进行线缆物理建模,并对线缆做两方面的假设:
(1) 几何方面。在刚性截面假设基础上,几何形态由中心线的移动和截面沿中心线的转动所体现,即将线缆作为一个轴向长度远远大于半径的空间圆柱体进行研究,且需满足:①中心线在变形前后均为二阶以上的光滑曲线;②活动线缆的长度和曲率半径远大于横截面的尺度;③相邻横截面可绕中心线作相对扭转,扭角为连续函数;④线缆在松弛状态下无原始曲率和扭率。
(2) 物理特性方面。将线缆等效为匀质、各向同性的圆截面弹性细杆,满足以下条件:①杆为均匀各向同性,应力和应变满足线性本构关系;②横截面为刚性平面,忽略弯曲引起的剪切变形,横截面与中心线正交。
1.1弹性杆的空间位姿描述
弹性杆为细长的可变形体,其可以呈现出弯曲、扭转等复杂的形态。弹性杆截面的几何中心连成空间曲线 C称为弹性杆的中心线,在刚性截面假定基础上,弹性杆的几何形态由截面沿中心线的移动和转动所体现,因此可以通过弹性杆中心线构建出弹性杆的外形。
为了方便描述弹性杆的空间姿态,需要建立多个坐标系。如图1所示,对于弹性杆的中心线C,以曲线上的一固定点 P0为原点建立弧坐标系 s,以空间中一固定点O建立参考坐标系(O−ξηζ) ,O点到空间中一点的向量为r。在曲线上任意一点P可定义一个依附于曲线的右手坐标系(P−NBT)称为Frenet坐标系,如图2所示。其中T为该点处切线方向上的单位矢量,N为该点处的法线方向上的单位矢量,矢量B由B=T×N得到。

图1 描述弹性杆的坐标系

图2 Frenet坐标系
仅通过 Frenet坐标系无法表示线缆的扭转变形,由于弹性杆的几何形态由截面沿中心线的移动和转动所体现,因此在截面中心点 P建立与刚性截面相固连的主轴坐标系(P−xyz),各坐标轴的单位矢量称为基矢量为d1、d2、d3,其中z轴与P点处的切线轴 T重合,即3= dT。主轴坐标系x轴与Frenet坐标系的N轴的夹角为θ,夹角θ为截面扭转变形的体现。
1.2主轴坐标系的空间位姿描述
主轴坐标系的姿态通过参考坐标系的旋转量表示,本文采用四元数表示旋转。
主轴坐标系基矢量为d1、d2、d3,参考坐标系基矢量为即:



1.3弹性杆的弯扭度
弹性杆的弯曲、扭转变形程度用弯扭度矢量u表示,中心线上任意一点 P处的弯扭度是该点处主轴坐标系的角位移对弧坐标s的变化率。与角速度的概念类似,且不同的是角位移是对时间 t的变化率。弯扭度等价于动点P沿着中心线沿弧坐标正向以单位速度做匀速运动时主轴坐标系的角速度。
在计算中使用四元数对弯扭度矢量进行表达,Schwab和Meijaard[21]推导出了四元数与旋转的角速度矢量的关系为:


计算得到在主轴坐标系中角速度矢量的各个分量为:
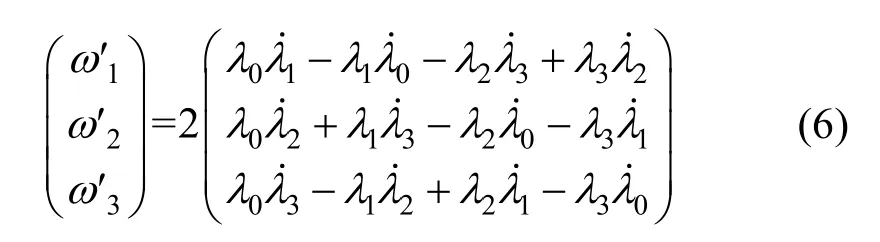
由于弯扭度矢量与角速度都是角位移的变化率,将式(6)中对时间变量t的微分改写为对弧坐标s的微分,可以得到弯扭度矢量u在主轴坐标系中的表达:

1.4弹性杆的能量表达式
处于平衡状态的曲杆只具有弹性势能,所以无需考虑运动过程中的动能以及耗散能。弹性势能包括拉伸形变具有的弹性势能 Vs和弯曲、扭转形变具有的弹性势能 Vb。文献[18]给出弹性杆的Cossserat理论中弹性势能表达,得到拉伸形变具有的弹性势能Vs的表达式为:

其中剪切变形被忽略。ks为抗拉刚度,其与拉伸杨氏模量Es有关,可通过计算得到。
弯曲和扭转变形所具有的弹性势能Vb与弯扭度矢量有关,见式(9):


其中,E为弯曲变形中的杨氏模量,G为扭转变形时的切变模量,r为截面半径。
对于理想杆,拉伸变形中的杨氏模量 Es等于弯曲变形时的杨氏模量E,由于实际线缆中存在多条线缆组成的线束,其截面并不均匀而且存在空隙,在实际测量中线缆拉伸时的杨氏模量 Es相比于弯曲时的杨氏模量E大。
1.5模型的约束
Cosserat杆模型是具有内在约束的系统,由于中心线上任意一点处的切线方向与该点处主轴坐标系的基矢量 d3的方向相同,所以存在方向一致约束:

对于四元数λ,只有当其模等于1时,才能表示为纯转动,因此存在四元数的标准化约束:

2 线缆的离散模型
在给出的Cosserat弹性杆的连续模型,包含两个关于弹性势能的积分式(8)和(9)以及两个对坐标的约束式(11)和(12)。在Cosserat弹性杆的应用中通常采用离散模型,文献[18]将弹性杆中心线离散为节点和线段,文献[19]采用弹簧质点模型模拟弹性杆。本文,采用Cosserat弹性杆理论建立线缆物理模型,并对线缆进行离散表达,根据线缆截面的刚性假设,线缆的几何形态由中心线决定。离散之后的线缆中心线为折线,已知各折线段中点的四元数和折线顶点的坐标,用代数式表达折线上各点的四元数和坐标,通过数值计算得到线缆的总能量。
2.1中心线的离散
如图3所示,对于没有分支的线缆取其中心线上的N个节点,顺序连接这些节点得到N−1条中心线段。第i个节点的位置由参考坐标系原点到节点的向量[1,N]表示,第j条中心线段对应的四元数由1]表示。

图3 线缆的离散模型
在对线缆进行离散后,式(8)和(9)中的微分项可以近似求出。第i与i+1个节点间的空间向量ir对弧坐标s的微分为:

其中,li是线缆处于自然状态时,第i条中心线段的长度。
第j条中心线段上四元数对弧坐标s的微分为:

其中,lj是曲杆处于自然状态时,第j条和第j+1条中心线段和的一半。
计算中近似给出第j条中心线段上任意一点处的四元数为:

2.2离散模型的能量表达式
将式(13)带入式(8)中,对第i条中心线段在长度li上进行积分,得到拉伸变形具有的弹性势能为:

将弯扭度用四元数表示,对第j条中心线段在长度lj上积分,得到弯曲、扭转变形具有的弹性势能为:

将上式代入式(14)和(15)可以进一步计算出到第j条中心线段弯曲、扭转变形具有的弹性势能,假设线缆在松弛状态下无原始弯扭度,那么uk(1≤k≤3)都为0。
3 求解离散模型的平衡状态
线缆敷设仿真中的核心是解决在线缆定长的情况下,其某一点运动时对线缆其他点的“联动”位置求解(即线缆的运动过程求解)[22]。Spillmann 和 Teschner[18]采用动力学方法求解弹性杆的运动过程,其方法存在振动现象,与现实中的线缆运动有一定差别,另外动力学方法中的时间步选择不当还会导致计算效率过低或结果不收敛。在线缆敷设过程中,对线缆的操作大多是在低速下完成的,没有明显的振动现象发生,忽略速度造成的影响认为其处于静力学平衡状态,所以线缆敷设仿真的关键是求解线缆处于平衡状态时的形态。
本文通过求解线缆弹性势能的优化问题,获得其有最小弹性势能的姿态,即线缆的平衡状态。其中线缆的弹性势能由Cosserat理论推导得出,并由罚函数将优化问题转化为无约束优化问题,最后采用信赖域方法对该优化问题进行求解。
3.1线缆弹性势能优化模型
通过式(16)和(17)计算出弹性杆具有的弹性势能为:

在一定约束下,当线缆具有最小弹性势能时,其处于平衡状态。本文通过求弹性势能 V的最小值,得到弹性杆的平衡状态。属于约束非线性最优化问题,优化模型为:

3.2优化模型中的约束施加
模型中存在多个等式约束,在处理计算机图形学约束的模型时,常用到罚函数方法。对于等式约束C(x)=0,将其转化为二次能量项加入目标函数中。当解不满足约束条件时,就增加目标函数的值。
其中方向一致约束变为:

四元数标准化约束变为:

在离散模型中对式(22)和(23)进行计算,得到每一段的罚函数能量表达式,其中方向一致约束为:

四元数标准化约束为:

引入罚函数把约束改写能量表达式(22)和(23),将约束最优化式(19)转化为无约束最优化问题:

文献[20]指出当抗弯刚度 kb1、kb2和抗扭刚度kb3较大时,弹性杆会发生“V”形的变形,其原因为弯曲和扭转变形集中于发生急剧变形处,其他部分不发生形变,导致“V”形部分的四元数的模接近于零。解决方法为改变四元数标准化约束能量式为:

当四元数的模为零时,能量将会变为无穷大,从而避免了以上问题的发生。但此方法会增加求解的困难,降低求解的效率。实际上产生上述问题的原因在于抗弯刚度和抗扭刚度过大使得罚函数的约束作用消失,通过增大罚函数罚因子系数同样可以防止这种情况发生,从而避免了改写四元数标准化约束形式引起的求解困难。
3.3能量优化模型的求解
文献[20]在一次求解步骤中顺序地采用了5种优化算法,即牛顿-高斯法、非线性共轭梯度法、线性共轭梯度法、最速下降法、一维搜索法,以保证得到能量优化问题的最优解。因为其原因是牛顿-高斯法只有初始值和最优解足够接近时,才能收敛。线缆的空间形态复杂,用以表示线缆形态的状态量较多,如式(24)中存在较多的变量,其初值往往难以给定,如果初始点与最优值差别较大,采用以上方法无法求得最优解。为了避免初始点选取的困难,本文采用信赖域方法[23],该算法为全局收敛方法,对初始点要求不高,使用该方法求解具有较高的稳定性。
3.4算法的计算效率
确保线缆模型求解的实时性是实现虚拟环境下线缆敷设过程仿真必须满足的要求,在确定罚函数罚因子系数及终止条件后,求解的效率主要由采用的优化算法决定。信赖域方法是全局收敛算法,初值不影响最优值的取得,但对求解时间有较大影响。当初值在最优值附近时,求解速度较快,由于操作过程相邻位置线缆状态变化不大,因此可将前一位置的线缆状态作为其后线缆位姿求解的初值,能够显著提高求解效率。图 4所示为17个位置求解时间,由于模型求解的第一位置,初值任意给定,求解时间较长,其后各位置求解耗时降低(计算时间控制在60 ms),满足了实时性要求。

图4 线缆各位置求解时间
4 线缆敷设仿真实例验证
采用本文提出的方法,开发了虚拟环境中的线缆敷设过程仿真软件系统,系统采用2.80 GHz Intel Core i5-2300 CPU,显卡为NVIDIA GeForce GT 240,内存4 GB,操作系统为Window 7 SP1。
该系统利用三维造型引擎 ACIS和三维显示交互工具包HOOPS建立三维环境,其中的结构件模型是在Pro/E中建模,并通过数据转换接口导入到本系统中。线缆的外形由物理模型计算得出,使用Matlab优化工具箱(Optimation Toolbox)求解模型中的能量优化问题,利用Matlab与C++的混合编程实现算法集成,以键盘和鼠标为输入设备,实现对线缆及其他虚拟物体的装配操作。
弹簧质点、能量曲线及逆运动学模型无法对线缆扭转变形进行模拟,但本文提出的物理模型能模拟这种形变,图 5所示为线缆操作中接头旋转,可真实反映线缆的扭转变形,并与真实情况相符。
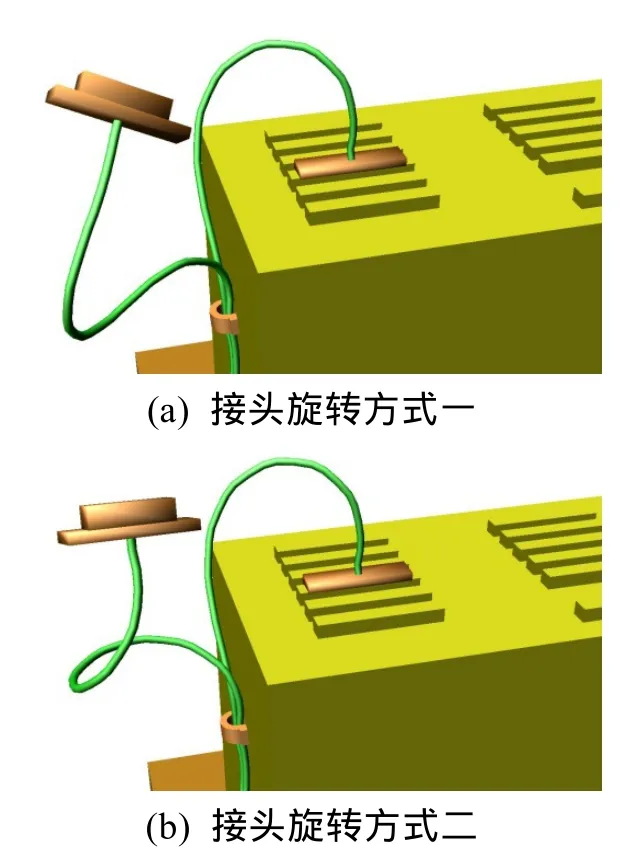
图5 线缆插装操作
对于多根线缆在敷设过程中通常需要捆扎,操作扎带可以带动线缆一起运动,捆扎效果如图6所示。
线缆敷设过程仿真实例如图 7所示,首先将所需的结构件模型和线缆模型导入虚拟环境中;然后将线缆移动到装配位置附近,操作接头可对接头进行插装,之后通过卡箍将线缆固定到结构件上,对于多根线缆用扎带进行捆扎,最终完成线缆的敷设。

图6 线缆捆扎及扎带调整

图7 线缆敷设过程仿真实例
5 结 论
(1) 针对面向柔性线缆敷设过程仿真的线缆物理建模问题,提出并建立了基于Cosserat弹性杆理论的柔性线缆物理模型,其考虑了线缆的弯曲和扭转变形,能够对敷设过程中线缆的形变进行真实的模拟。
(2) 通过罚函数方法对模型中的约束进行转化,选取适当的罚因子系数,实现了模型中的四元数标准化约束和方向一致约束。
(3) 采用信赖域方法求解线缆模型中的非线性优化问题,该方法具有全局收敛特性,避免了初始点难以确定的问题,并采用将上一位置的线缆状态作为线缆下一位置模型计算的初始点的方法,提高了线缆物理模型求解的效率,满足了虚拟环境下线缆敷设仿真的实时性要求。
(4) 开发了虚拟环境中的线缆敷设过程仿真软件系统,通过实例验证了线缆物理模型的可行性,后续工作将考虑建立分支线缆的物理模型。
[1] 王发麟, 廖文和, 郭宇, 等. 复杂机电产品线缆信息本体表达与存储分析[J]. 图学学报, 2015, 36(3): 376-383.
[2] 刘检华, 万毕乐, 宁汝新. 虚拟环境下基于离散控制点的线缆装配规划技术[J]. 机械工程学报, 2006, 42(8): 125-130.
[3] 杨守勇. 三维线缆建模及布线设计的研究与实现[D].大连: 大连理工大学, 2012.
[4] Eischen J W, Deng S, Clapp T G. Finite-element modeling and control of flexible fabric parts [J]. IEEE Computer Graphics and Applications, 1996, 16(5): 71-80.
[5] 魏发远, 王峰军, 陈新发. 含有柔性电缆的复杂系统装配仿真[J]. 工程设计学报, 2007, 14(1): 25-31.
[6] Hergenröther E, Dähne P. Real-time virtual cables based on kinematic simulation [C]//WSCG ’2000, The 8th International Conference in Central Europe on Computer Graphics, Visualization and Interactive Digital Media 2000. Plzen, Czech Republic, 2000: 402-409.
[7] Terzopoulos D, Qin H. Dynamic NURBS with geometricconstraints for interactive sculpting [J]. ACM Transactions on Graphics (TOG), 1994, 13(2): 103-136.
[8] 王志斌, 刘检华, 刘佳顺, 等. 电缆虚拟布线中的物理特性分析与布局设计技术[J]. 计算机辅助设计与图形学学报, 2014, 26(7): 1193-1202.
[9] 尚炜, 宁汝新, 刘检华, 等. 复杂机电产品中的柔性线缆装配过程仿真技术[J]. 计算机辅助设计与图形学学报, 2012, 24(6): 822-831.
[10] 王志斌. 虚拟环境下基于物理属性的线缆布局与装配仿真技术[D]. 北京: 北京理工大学, 2014.
[11] 王志斌, 刘检华, 刘佳顺, 等. 面向电缆虚拟装配仿真的多分支弹簧质点模型[J]. 机械工程学报, 2014, 50(3): 174-183.
[12] Loock A, Schömer E, Stadtwald I. A virtual environment for interactive assembly simulation: from rigid bodies to deformable cables [C]//5th World Multiconference on Systemics, Cybernetics and Informatics (SCI’01). Orlando, Florida, USA, 2001: 325-332.
[13] 刘延柱. 弹性细杆非线性力学[M]. 北京: 清华大学出版社, 2006: 15-19.
[14] 刘检华, 赵涛, 王春生, 等. 虚拟环境下的活动线缆物理特性建模与运动仿真技术[J]. 机械工程学报, 2011, 47(9): 117-124.
[15] Bertails F, Audoly B, Cani M P, et al. Super-helices for predicting the dynamics of natural hair [J]. ACM Transactions on Graphics (TOG), 2006, 25(3): 1180-1187.
[16] Bergou M, Wardetzky M, Robinson S, et al. Discrete elastic rods [J]. ACM Transactions on Graphics (TOG), 2008, 27(3): 63:1-63:12.
[17] Pai D K. Strands: interactive simulation of thin solids using cosserat models [J]. Computer Graphics Forum, 2002, 21(3): 347-352.
[18] Spillmann J, Teschner M. C o R d E: Cosserat rod elements for the dynamic simulation of one-dimensional elastic objects [C]//Proceedings of the 2007 ACM SIGGRAPH, Eurographics Symposium on Computer Animation. Eurographics Association, 2007: 63-72.
[19] 黄劲, 沈中伟, 王青, 等. 基于优化的大步长准静态线缆模拟[J]. 计算机辅助设计与图形学学报, 2011, 23(1): 1-10.
[20] Grégoire M, Schömer E. Interactive simulation of one-dimensional flexible parts [J]. Computer-Aided Design, 2007, 39(8): 694-707.
[21] Schwab A L, Meijaard J P. How to draw Euler angles and utilize Euler parameters [C]//ASME 2006 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2006: 259-265.
[22] 刘检华, 万毕乐, 孙刚, 等. 线缆虚拟布线与敷设过程仿真技术[J]. 计算机集成制造系统, 2012, 18(4): 787-795.
[23] 张光澄, 王文娟, 韩会磊, 等. 非线性优化计算方法[M]. 北京: 高等教育出版社, 2005: 146-159.
Physical Characteristic Oriented Modeling for Flexible Cable Harness Based on Cosserat Elastic Rod Theory
Lin Haili,Liu Jianhua,Tang Chengtong,Liu Jiashun
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)
To simulate laying process of cable harness, a physical characteristic oriented modeling for flexible cable harness is proposed based on Cosserat elastic rod theory. The cable’s total energy is obtained by applying Cosserat elastic rod theory on discrete cable model. The cable’s configuration with the lowest energy can be obtained by using optimization algorithm, which is the equilibrium state. The model takes into consideration the flexibility and continuity of the cable, which could simulate bending and twisting. From the discrete expression of the cable, the cable’s energy can be calculated by numerical method. And penalty method is used to convert the constraint problem to an unconstrained problem. The trust region algorithm is implemented to get the configuration of the cable with minimum potential energy. This method is applied in the simulation of cable laying process in a virtual environment and a prototype system is developed, and the model is validated by this system.
cable harness; physical modeling; laying simulation; Cosserat elastic rod theory; energy minimizing
TP 391.9
10.11996/JG.j.2095-302X.2016010034
A
2095-302X(2015)01-0034-09
2015-09-24;定稿日期:2015-10-15
林海立(1991–),男,四川西昌人,硕士研究生。主要研究方向为计算机辅助设计。E-mail:linhailisc@163.com
刘检华(1977–),男,江西萍乡人,教授,博士,博士生导师。主要研究方向为复杂产品装配与检测。E-mail:jeffliu@bit.edu.cn
——《势能》

