基于分段三次函数的最大熵方法的收敛性

王 洁，王 涛

(哈尔滨师范大学)



基于分段三次函数的最大熵方法的收敛性

王 洁，王 涛

(哈尔滨师范大学)

提出了分段三次函数最大熵方法，通过求解Frobenius-Perron算子方程不动点给出了稳态密度的估计，证明了方法的收敛性并说明了在一定条件下方法的收敛速度可以达到O(n-4).

最大熵；分段三次函数；密度函数

0 引言

最大熵方法是一种数值计算方法，由Jayne在1957年首次提出，用来解决有限齐次的Hausdorff矩问题，并给出了不变映射S:[0,1]→[0,1]的稳态密度. 这种方法的有效性和简便性受到越来越多的学者关注，并用来解决各领域的问题[1-3].

原始的最大熵方法是用以{1,x,x2,…,xn}为基的多项式进行运算求解，在方法的运算过程中需要求解非线性方程，但有时用这种方法计算矩会产生很大的条件数，从而引起函数值的相对误差较大，因此导致了最大熵方法应用上的困难.为了克服这些困难，一些学者提出了改进的最大熵方法，如利用正交多项式基代替原来的多项式基等[4]. Ding在文献[5]中提出了一种分段常数最大熵方法，将非线性方程的求解转换为线性方程的求解，取得了较好的效果.为了增加算法的收敛速度，2011年Ding又提出应用分段线性函数来估计稳态密度[6]，这种方法有效，且收敛速度达到了O(n-2).2015年他又进一步提出分段二次函数最大熵方法[7]，该方法的收敛速度是O(n-3).

该文提出了基于分段三次函数的最大熵方法，通过第二节的计算与证明可以得出，在一定的条件下提出的方法收敛的速度更快，可以达到O(n-4).

1 预备知识

在最大熵方法中，非线性函数H是一个Boltzmann熵，定义为：

它满足的约束条件为

(1)

其中D≡{f ≥0:f ∈L1(0,1),‖f‖1=1}是所有密度函数组成的集合，{g1,g2,…,gk}⊂L∞(0,1)，m1,m2，…，mk是给定的k个常量. 最大熵方法的核心就是解决如下的最大熵问题,

1≤i≤r}

(2)

Lasota和Mackey在文献[8]中首先给出了满足约束条件(1)的最大熵问题(2)的解为

2 分段三次函数最大熵方法的收敛性

令S:[0,1]→[0,1]是一个非线性变换，使得相应的Frobenius-Perron算子的不动点方程Psf=f有解f*.由文献[6]知道，当f*满足一定的光滑性条件时，密度函数的最大熵估计依范数收敛于f*.

Δn={φ:φ∈C0[0,1],φ|Ii∈P3(Ii),i=1,2,…,n}

其中C0[0,1]是定义在[0,1]上的连续函数，P3(Ii)是定义在Ii上的三次函数空间.定义

集合{φ0,φ1,…,φ2n}是2n+1维向量，它是Δn空间的一组基，满足

将分段三次函数φi代入上述最大熵问题(2)，由文献[7]可知最大熵问题的解为

构造基函数φ0,φ1,…,φn如下：

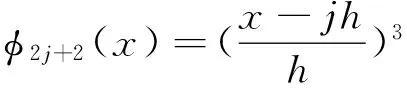
定理1 令g∈C4[0,1]，设

p(x)=aφ2j(x)+bφ2j+2(x)+cφ2j+2(x)

其中x∈[xj,xj+1]⊆[0,1]，j=0,1,…,n-1，且对∀x,y∈[0,1]，有g(x)-g(y)≤(x-y)4，那么g(x)-p(x)=O(h4).

证明 由于

将g(x)在x=jh处用泰勒公式展开后有

其中ξ∈(jh,x)，则

(3)

由于g(x)-g(y)≤(x-y)4，可知g(x)-p(x)=O(h4)，定理证毕.

定理2 令g∈C4[0,1],φ0,φ1,…,φn是分段三次函数的基，那么

证明 在每一个子区间[xj,xj+1],j=0,1,2,…,n-1上应用定理1即可完成证明.

证明 仿照文献[7]定理4.5的证明即可得到定理3.

[1] Mead LR, Papanicolaou N. Maximum entropy in the problem of moments [J]. J Math Phys, 1984(25): 2404-2417.

[2] Ding J. A maximum entropy method for solving Frobenius-Perron operator equations [J]. Appl Math Comput, 1998(93): 155-168.

[3] Ding J, Mead L. Maximum entropy approximation for Lyapunov exponents of chaotic maps [J]. J Math Phys 2002(43): 2518-2522.

[4] Ding J, Rhee N. A maximum entropy method based on orthogonal polynomials for Frobenius-Perron operators [J]. Adv Appl Math Mech, 2011, 3(2): 204-218.

[5] Ding J, Rhee NH. Birkhoff’s ergodic theorem and the piecewise-constant maximum entropy method for Frobenius-Perron operators [J]. Int J Comput Math, 2012(89):1083-1091.

[6] Ding J, Jin C, Rhee NH. A maximum entropy method based on piecewise linear functions for the recovery of a stationary density of interval mappings [J]. J Stat Phys, 2011(145): 1620-1639.

[7] Upadhyay T, Ding J, Rhee NH. A piecewise quadratic maximum entropy method for the statistical study of chaos [J]. J. Math Anal Appl, 2015(421): 1487-1501.

[8] Lasota A, Mackey M. Chaos, Fractals and Noises [M]. New York: Spring-Verlag, 1994.

(责任编辑：季春阳)

Convergence of A Maximum Entropy Method Based on Piecewise Cubic Function

Wang Jie, Wang Tao

(Harbin Normal University)

A maximum entropy method based on piecewise cubic function is proposed in this paper. By solving Frobenius-Perronoperator equation, the stationary density estimation is given, which is the fixed point of the operator. Then the convergence of the given method is proved, with the rate O(n-4).

Maximum entropy; Piecewise cubic function; Density function

2016-01-15

O211

A

1000-5617(2016)02-0040-03