基于布尔代数理论的农林牧复合生态系统可达性研究*

于 娇,顾凤岐

(东北林业大学)



基于布尔代数理论的农林牧复合生态系统可达性研究*

于 娇,顾凤岐**

(东北林业大学)

将黑龙江省集贤县的农林牧复合生态系统建立结构模型，细分系统的九个分室，作出系统结构的有向图，并给出有向图的邻接矩阵，进而由布尔代数的相关理论求出系统的可达矩阵，由可达矩阵考虑系统的可达性，可达性反映出系统的稳定性，这对于农林牧复合生态系统的研究具有重要的意义.

布尔代数；农林牧复合生态系统；可达矩阵；稳定性

0 引言

19世纪30年代，布尔偶然读到一些介绍数学知识的教科书，由此布尔对数学产生了浓厚的兴趣，尤其是对代数关系的对称和美有着很强的感觉.他用数学方法把逻辑简化为一种极其容易和简单的代数，成功地建立了逻辑演算.他用等式表示判断，把推理看作等式的变换.这种变换的有效性不依赖人们对符号的解释，只依赖于符号的组合规律[1].这一逻辑理论人们常称它为布尔代数.开始研究布尔代数，也叫逻辑代数.19世纪50年代，布尔代数问世了，这在数学史上无疑是设立了一个新的里程碑.如今，布尔代数已发展成为纯数学理论的一个重要的分支.

1 布尔代数在结构模型中的应用

对于一个复杂的系统而言，建立一个直观的结构模型对系统的研究是十分必要的.结构模型有三要素，分别是有向图，邻接矩阵以及可达矩阵.

1.1 有向图

有向图是最简单的方式用来表达系统中各部分之间的宏观关系.如果要素Si对Sj有影响，则在图中由Si到Sj用一条有向线段连接起来，方向从Si指向Sj，不断重复这种连接方式便构成了有向图，如图1所示.

图1

1.2 邻接矩阵

结构模型可用矩阵形式来描述，除了用有向图表示系统结构关系之外，还可用有向图对应的矩阵表示系统结构关系，这种矩阵叫做关系矩阵，其中最直接的一种叫做邻接矩阵，用来表示各单元之间直接的连接关系[2].邻接矩阵是一种布尔矩阵，其运算方法遵循布尔代数的运算规则.

对于有n个要素的系统(S1,S2,S3,…,Sn)，定义邻接矩阵A如下：

由图论可知，邻接矩阵与有向图是一一对应的关系，由邻接矩阵可以画出唯一的有向图，反之，根据有向图可写出唯一的邻接矩阵.

1.3 可达矩阵

在定义可达矩阵之前，先引入布尔矩阵.

定义1[3]将元素取值于{0,1}且矩阵运算由∨和∧ 定义的矩阵称为布尔矩阵，运算符∨和运算符∧分别叫做“逻辑加”和“逻辑乘”.其中， 0∨0=0∧0=1∧0=0∧1=0,1∨0=0∨1=1∨1=1∧1=1.

由此可见，邻接矩阵是一个布尔矩阵，其算法自然满足布尔运算规则，通俗的讲，矩阵运算的过程中，矩阵中的元素满足布尔算法1+1=1，1+0=0+1=1，1×1=1，1×0=0×1=0.

假设某系统由S1，S2，S3，S4，S5五部分组成，作出系统的有向图，该有向图的邻接矩阵为：

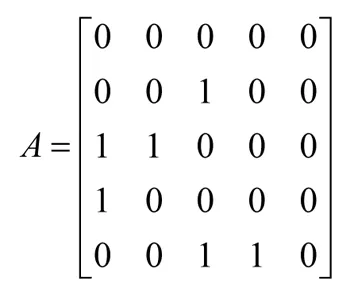
在上述邻接矩阵A上加一个单位矩阵I可得：

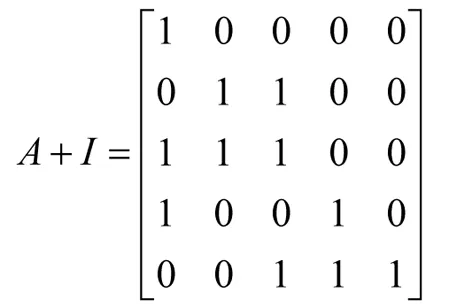
矩阵A+I描述了各点间经长度为0和1(不大于1)的路的可达情况.同样，(A+I)2描述了各点间经长度不大于2的路的可达情况.应该说明的是，在此所做的加法和乘法运算均为布尔运算[4].若经运算后有如下关系式：

(A+I)i-2≠(A+I)i-1≠(A+I)i+1=M,i≤n-1.

则矩阵M称为可达矩阵.它表明了各点间经长度不大于n-1的通道的可达情况.可达矩阵M的元素mii为1代表要素Si到Sj存在可到达的路径，对于点数为n的图，最长的通道(即路径)不能超过n-1.此外，M=M2.

可达矩阵是判别一个有向图是否为强连通图或弱连通图的有效工具[5]，因此通过可达矩阵可以检验整个系统的紧密连接程度.求得有向图可达矩阵的方法有很多[6]，该文利用布尔矩阵的运算性质求有向图的可达矩阵.

如上例中有：

所以可达矩阵M=(A+I)2，由此可知S2可达S1和S3，S3可达S1和S2， S4可达S1， S5可达 S1、S2、S3、S4.即可达矩阵完全表示出了各单元间的直接关系，它能够很好的把握系统结构，判断系统的连通程度强弱.

用传统矩阵布尔代数算法每迭代一次需要花费布尔代数乘法n3个，布尔代数加法n2(n-1)个[7].由此可见计算量是相当大的.因此对于阶数较大的邻接矩阵，通常借助于计算机来完成迭代.

2 农林牧复合生态系统的可达性分析

2.1 系统结构模型的建立

将集贤县农林牧复合生态系统分为籽粒(X1)，秸秆(X2)，根(X3)，畜牧业(X4)，青贮(X5)，土壤有机质(X6)，人口(X7)，肥料(X8)以及林业(X9)九个分室.外界环境记为(X0).系统结构模型的有向图如图2所示.

图2 系统结构模型的有向图

2.2 系统结构模型的可达性分析

由系统的有向图可作出系统的邻接矩阵，A=(aij)，(i,j=0,1,2,…,9)，当i或j等于0时，表示的是外界与系统的物质交换情况.可得：

对上述邻接矩阵A加上一个单位矩阵I，可得：

那么

以此类推，由于矩阵的阶数较大，所以借助于计算机来求解，由matlab计算可得：

矩阵M称为可达矩阵，由上式可知，可达矩阵的元素几乎全为1，这表明图中绝大多数点都可以到达其他各点.

3 结束语

该文建立了农林牧复合生态系统的结构模型，并由该结构模型作出了有向图，建立了系统的邻接矩阵.基于布尔代数的相关理论求解系统的可达矩阵，并对系统的可达性进行研究，研究结果表明，生态系统中的绝大部分单元能够到达系统中的其他各点，整个生态系统是紧密连接在一起的，该农林牧复合生态系统稳定性比较强.布尔代数算法将计算过程进行了简化，不必考虑具体数值，而是通过1和0来表现出系统内单元之间的可达与否，进而判断出系统的强弱连接程度.布尔代数理论对整个计算过程起到了至关重要的作用.

[1] 刘晓利.有向图的强连通性分析及判别算法[J].计算机应用与软件,2005,22(4):138-139.

[2] 高广学.简化可达性矩阵的计算[J].齐齐哈尔大学学报,1999,15(4):42-44.

[3] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1997.

[4] 张立昂,刘田,译.计算理论基础[M].北京:清华大学出版社,2000.

[5] Kim K H.Boolean matrix theory and application[M].New York:Dekker,1982.

[6] 肖人彬.基于系统结构建模分析的骨架矩阵代数求法[J].华中理工大学学报,1997,25(7):46-48.

[7] 喻湘存,熊曙初.系统工程教程[M].北京：清华大学出版社,北京交通大学出版社,2006.

(责任编辑：于达)

Accessibility of Animal Husbandry Compound Ecosystem Research Based on the Theory of Boolean Algebra

Yu Jiao， Gu Fengqi

(Northeast Forestry University)

In this article, animal husbandry compound ecological system structure model of the jixian county of heilongjiang province is set up, nine points of the room in system are segmentated, the system structure of directed graph is made, and adjacency matrix of directed graph is given. And then the accessible matrix of the system is given by the theory of Boolean algebra, and accessibility reflects the stability of the system by considering the reachable matrix system accessibility, The research of animal husbandry compound ecosystem has the vital significance.

Boolean algebra;Animal husbandry compound ecosystem;Accessible matrix;Stability

2016-01-25

*黑龙江省自然科学基金资助项目(C0224)

**通讯作者

O153.2

A

1000-5617(2016)02-0036-04