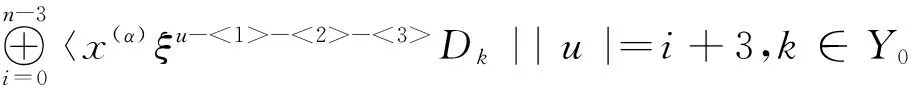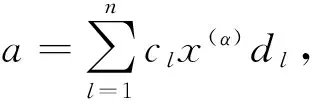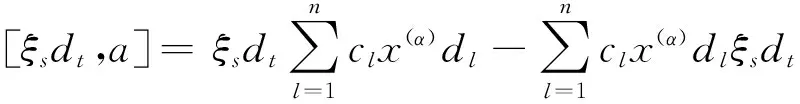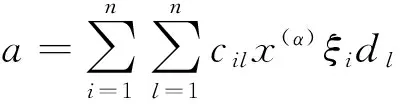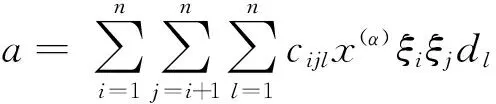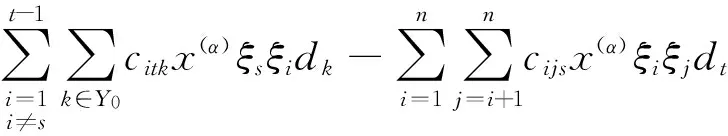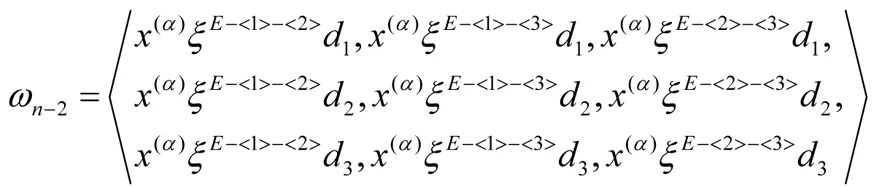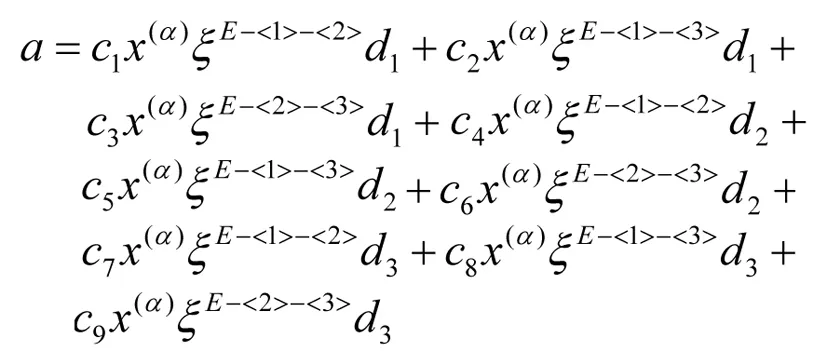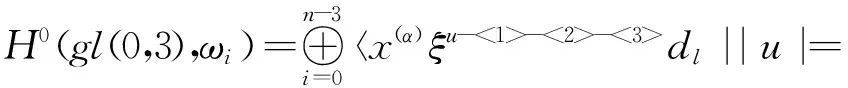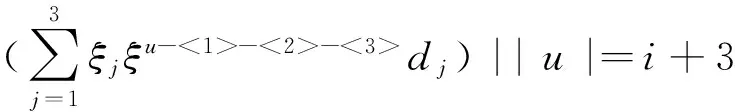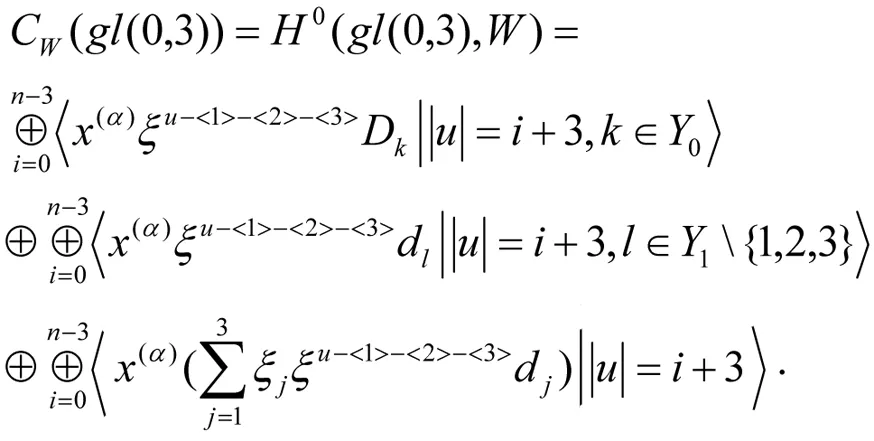素特征域上gl(0,3)在广义Witt李超代数中的中心化子*

田丽媛, 侯 莹, 郑克礼

(东北林业大学)



素特征域上gl(0,3)在广义Witt李超代数中的中心化子*

田丽媛, 侯 莹, 郑克礼**

(东北林业大学)

主要研究素特征域上gl(0,3)在广义Witt李超代数W中的中心化子，其中gl(0,3)是一般线性李超代数的一个子代数, 并且同构于W的一个子代数. 计算从gl(0,3)到广义Witt型李超代数的每个子模的中心化子. 并利用解线性方程组的方法确定gl(0,3)在广义Witt李超代数中的中心化子.

中心化子; 子代数; 零维上同调群; 线性方程组

0 引言

李超代数最早起源于理论物理中超对称现象的研究. 作为超对称的数学模型, 李超代数在数学和物理学中多学科都有及其重要的应用[1]. 对于非模李超代数的研究已经有了很多深入的结论[2]. 而模李超代数正处在发展阶段, 还有许多问题需要解决[3]，比如Cartan型单模李代数的分类问题, 这方面的研究工作对进一步发展和完善这一理论尤为重要. 中心化子的概念起源于群结构的研究[4]. 中心化子不仅仅是一个子集, 还是一个子代数. 作为李(超)群的线性化对象, 李(超)代数自然也存在着中心化子[2,5]. 由于对于伴随表示一个李(超)代数可以做为其子代数的自然模, 则中心化子可以等价的看作零维上同调群. 近年来Cartan型模李超代数低维上同调群(即内外导子)被大量的研究(参见文献[6]及其参考文献). 文献[7]对系数在Witt上的单模李超代数gl2|1的低维上同调进行了深入研究, 给出了解决此类问题的同调方法. 因为线性李超代数的低维上同调群对于李超代数的分类具有重大意义, 所以这也是该文研究素特征域上一类一般线性李代数在李超代数模上的中心化子的主要动机.

该文在素特征域上分别计算了H0(gl(0,3),w)与H0(gl(0,3),ω), 借助已有结论与解方程组的方法表示出系数在广义Witt李超代数上的gl(0,3)的零维上同调, 即得到gl(0,3)在广义Witt李超代数中的中心化子结构.

1 素特征域上的CW(gl(0,3))

[8], 广义Witt李超代数W有如下结构：

W=w⊕ω,

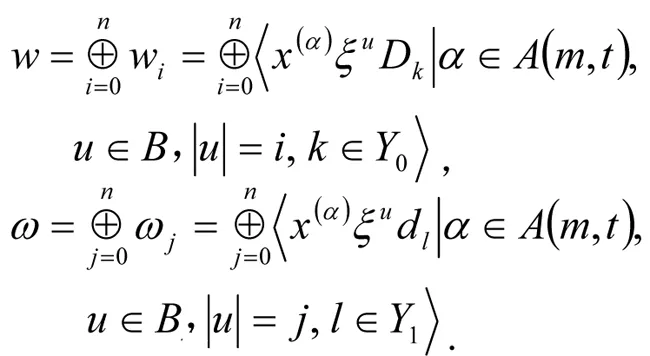
显然{eij|i,j=1,2,3}是gl(0,3)的标准基, 其中eij是(i,j)位置为1其他位置为0的矩阵. 由于gl(0,3)是李代数， 可以证明gl(0,3)同构于W的子代数〈ξidj|i,j=1,2,3〉. 则W可通过伴随表示看作gl(0,3)-模. 因此存在系数在W上的gl(0,3)的n-维上同调群.

由于H0(gl(0,3),W)=H0(gl(0,3),w)⊕H0(gl(0,3),w). 为了决定素特征域上的CW(gl(0,3)), 只需要对所有的i=0,1,…,n考虑零维上同调H0(gl(0,3),wi)与H0(gl(0,3),wi)即可. 首先, 将考虑零维上同调群H0(gl(0,3),w).

命题1 H0(gl(0,3),w0)=〈x(α)Dk|k∈Y0〉

证明 由定义有w0=〈X(α)Dk|k∈Y0〉对任意的y∈gl(0,3)有[y,x(α)Dk]=0, 则

H0(gl(0,3),w0)=w0=〈x(α)Dk|k∈Y0〉

命题2 H0(gl(0,3),w1)=〈x(α)ξiDk|i∈Y1{1,2,3},k∈Y0〉.

证明 由定义有w1=〈x(α)ξiDk|i∈Y1,

k∈Y0〉. 设存在

其中cik∈F, 满足[gl(0,3),a]=0. 设s=1,2,3; t=1,2,3,则

已知Dk是线性无关的, 所以ctk=0(t=1,2,3).

这意味着对所有的y∈gl(0,3)i∈Y1{1,2,3}与k∈Y0有[y,x(α)ξiDk]=0.

命题3 H0(gl(0,3),w2)=〈x(α)ξiξjDk|i,j∈Y1{1,2,3},k∈Y0〉.

证明 由定义有w2=〈x(α)ξiξjDk|i,j∈Y1且i

其中cijk∈F, 满足[gl(0,3),a]=0. 设s=1,2,3;t=1,2,3, 则

已知Dk是线性无关的, 得

c1jk=0(j∈Y1{1})

c2jk=0(j∈Y1{1,2})

c3jk=0(j∈Y1{1,2,3})

这意味着对所有的y∈gl(0,3),i∈Y1{1,2,3}与k∈Y0有[y,x(α)ξiξjDk]=0.

推论1 H0(gl(0,3),wi)=

〈x(α)ξu-<1>-<2>-<3>Dk||u|=i+3,k∈Y0,0≤i≤n-3〉.

命题4 H0(gl(0,3),wn-2)=0.

证明 由文献[8]已知H0(gl(0,2),wn-2)=〈x(α)ξE-<1>-<2>Dk〉, 显然H0(gl(0,3),wn-2)是H0(gl(0,2),wn-2)的子集. 设存在

则H0(gl(0,3),wn-2)=0.

命题5 H0(gl(0,3),wn-1)=H0(gl(0,3),wn)=0.

定理1 H0(gl(0,3),w)=

其次, 对于所有i=0,1,…,n, 考虑零维上同调H0(gl(0,3),ωi).

命题6 H0(gl(0,3),ω0)=〈x(α)dl|l∈Y1{1,2,3}〉.

-csx(α)dt=0

则cs=0 (s=1,2,3).

命题7 H0(gl(0,3),ω1)=〈x(α)ξidl|i,l∈Y1{1,2,3}>⊕〈x(α)(ξ1d1+ξ2d2+ξ3d3)〉.

则ctl=cis=0(t,s=1,2,3), 但c11=c22=c33.

因此H0(gl(0,3),ω1)=〈x(α)ξidl|i,l∈Y1{1,2,3}〉⊕〈x(α)(ξ1d1+ξ2d2+ξ3d3)〉.

命题8 以下命题成立： .

证明 由定义有ω2=〈x(α)ξiξjdl|i,j,l∈Y1〉对任意的a∈ω1有

设s=1,2,3;t=1,2,3,则

推论2 以下结论成立：

H0(gl(0,3),ωi)=〈x(α)ξu-<1>-<2>-<3>dl||u|=i+3,l∈Y1{1,2,3}〉⊕

其中1≤i≤n-3.

命题9 H0(gl(0,3),ωn-2)=

x(α)ξE-<2>-<3>d1+x(α)ξE-<1>-<3>d2+

x(α)ξE-<1>-<3>d3.

证明 显然地,ωn-2=〈x(α)ξE--dl|i,j,l∈Y1|〉, 以下通过分别考虑两种情形来完成此命题的证明.

(i)如果i,j,l=1,2,3. 则

设存在

设s=1,2,3; t=1,2,3, 令[ξsdt,a]=0,则c1=c2=c4=c6=c8=c9=0, c3=c5=c7即可.

因此有H0(gl(0,3),ωn-2)=

x(α)ξE-<2>-<3>d1+c5x(α)ξE-<1>-<3>d2+

x(α)ξE-<1>-<2>d3.

(ii) i,j,l≠1,2,3, 则易得H0(gl(0,3),ωn-2)为零.

综上所述, 结论得证.

命题10 H0(gl(0,3),ωn-1)=0

证明 已知H0(gl(0,2),ωn-1)=x(α)ξE-<1>d2+x(α)ξE-<2>d1, 显然H0(gl(0,3),ωn-1)是H0(gl(0,2),ωn-1)子集, 又有

[ξ1d3,x(α)ξE-<1>d2+x(α)ξE-<2>d1]≠0.

则H0(gl(0,3),ωn-1)=0.

命题11 H0(gl(0,3),ωn)=0.

定理2 以下结论成立：

最终,由定理1与定理2 得以下定理.

定理3 以下结论成立：

参 考 文 献

[1] Fayet P, Ferrara S. Supersymmetry [J], Phys Rep,1977,32:5:249-334.

[2] Scheunert M. Theory of Lie superalgebras. An introduction [M]. Springer-Verlay, 1979.

[3] 张永正, 刘文德. 模李超代数 [M].科学出版社, 2004.

[4] Jacobson N. Basic algebra I (2 ed.) [M], Dover Publications, 2009.

[5] Jacobson N. Lie algebras [M]. Interscience Publshers, New York, 1962.

[6] Bai W. and Liu W D. Superderivations for modular graded Lie superalgebras of Cartan type [J]. Algebr. Represent. Theor, 2014, 17: 69-86.

[7] 孙丽萍, 远继霞, 刘文德. 李超代数gl2|1到Witt 超代数的低维上同调 [J]. 数学实践与认识, 2013, 43: 239-243.

[8] 郑克礼. 李超代数的若干结构与表示[D]. 博士学位论文：东北师范大学, 2014.The Centralizer of gl(0, 3) in the Generalized Witt Lie Superalgebra Over Fields of Prime Characteristic

(责任编辑：于达)

Tian Liyuan, Hou Ying, Zheng Keli

(Northeast Forestry University)

In this paper, the centralizer ofgl(0,3) in the generalized Witt Lie superalgebrasWover fields of prime characteristic is studied, wheregl(0,3) is a subalgebra of the general linear Lie superalgebra, and it is isomorphic to a subalgebra ofW. The centralizer ofgl(0,3) in each submodule of the generalized Witt Lie superalgebras is calculated. Using the method of solving system of linear equations, the centralizer of thegl(0,3) in generalized Witt Lie superalgebras is determined.

Centralizer; Lie superalgebra; Zero cohomology group; System of linear equations

2016-02-24

*黑龙江省东北林业大学大学生创新项目(1022520152620);中央高校基本科研业务费专项资金资助(2572015BX04);国家自然科学基金资助(11171055, 11471090)

**通讯作者: zhengkl@nefu.edu.cn

O

A

1000-5617(2016)02-0005-03