基于MATLAB四旋翼姿态航向仿真*

代 君,刘战合,王 菁

(郑州航空工业管理学院)



基于MATLAB四旋翼姿态航向仿真*

代 君,刘战合,王 菁

(郑州航空工业管理学院)

基于互补滤波下的信息融合算法，将实验获得的MTI小型姿态航向参考系统中惯性器件的实际数据进行仿真分析，在比较了陀螺仪积分、加速度计计算、互补滤波法得到的姿态角效果后，最终分析了互补滤波理论应用于姿态航向解算中的优化效果.

姿态航向参考系统；互补滤波；MTI

0 引言

近十几年来，四旋翼飞行器逐渐走入人们的日常生活，四旋翼飞行器在电子技术飞速发展的促进下日益趋向小型化.

四旋翼飞行器主要依靠四个旋翼产生升力，通过改变各个旋翼的升力大小，可以控制四旋翼的飞行方向与飞行姿态.而对于四旋翼姿态航向参考系统来讲，惯性传感器是必不可少的.惯性传感器包括陀螺仪、加速度计以及磁强计 ，通过这些安装在四旋翼上的传感器所测得的数据，计算机可以计算出四旋翼的姿态及航向.

四旋翼姿态航向系统，顾名思义，就是为飞行控制人员测量、提供并显示姿态角(包括俯仰角和滚转角)和航向角的系统，使飞行控制人员能够根据这些数据及时调整操作，达到飞行目的 .对于四旋翼姿态航向的计算算法进行研究，可以使四旋翼飞行器的姿态角、航向角、偏航角的误差更小，提高系统定位精度.研究算法需从无人机的姿态信息融合系统着手，这种参考系统由微加速度计、磁航向计、微型陀螺仪组成.加速度计和磁航向计组合可以计算得到俯仰角、滚转角、偏航角；陀螺仪通过测量三个方向的角速度，通过积分即可算出姿态角. 但是这两种方法都有所缺陷，计算得到的姿态角误差均比较大.因此要寻求一种更为有效的算法来解决这些问题，即为该文所要论述的方法——互补滤波算法.这种算法可以满足四旋翼导航控制系统的可靠度、精度的要求，因此具有重要的理论和现实意义.

1 互补滤波

互补滤波器可以分别给陀螺仪和加速度计的测量数据赋予加权系数，使得四旋翼飞行器的姿态角在静态时主要依靠加速度计的测量值，大机动时主要依靠陀螺仪的测量值.

1.1 互补滤波器原理

滤波器包括低通滤波器、高通滤波器、采样周期、时间常量等 .

(1)低通滤波器.目标是滤除高频数据，留下低频数据.如angle=0.98*angle+0.02*x_acc;(加速度传感器通过低通滤波器)

(2)高通滤波器.与低通滤波概念相反，能用来抑制陀螺漂移.

(3)采样周期.该次仿真采样率为100 Hz，即采样周期为0.01 s.

(4)时间常量.滤波器的时间常数是信号作用的相对时间.

(5)互补滤波则是通过给低通和高通滤波器赋予一定的加权系数，使其输出一个有意义的、准确的线性估计.如图1所示：

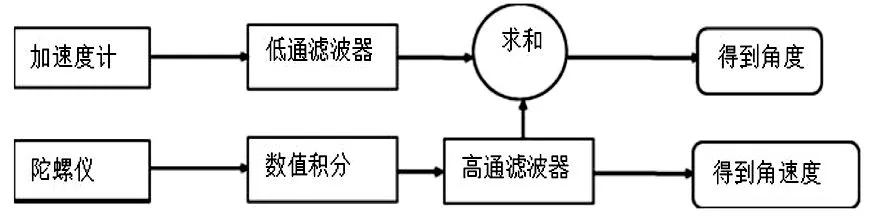
图1 互补滤波原理图

1.2 互补滤波算法[4]

根据陀螺仪和加速度计在频域上互补的特性，可以用互补滤波算法结合它们的优点.互补滤波器的传递函数如下：

(1)

(2)

将式(2)带入重力场及地磁场分量的微分方程即

(3)

四旋翼平衡时，加速度计的输出是：

fb=a-gb+n1

(4)

其中，fb为比力向量; a为加速度向量； gb为重力加速度； n1为噪声向量.磁强计输出为：

(5)

由式(3)和(4)，得：

(6)

由式(3)和(5)，得：

(7)

由式(6)、(7)，可以得到重力场和地磁场的互补滤波器的时域方程为：

(8)

(9)

通过互补滤波，将三种惯性器件进行优势互补，使得长时间情况下保持姿态解算的高精度且不会发生陀螺的漂移.

2 姿态航向仿真分析

2.1 硬件介绍

MTI[5]输出的数据非常全面，包括三维加速度计、三维陀螺仪和三维磁强计数据.此外，它还直接输出姿态角和航向角，可以为该次仿真作为参照，见表1.

表1 MTI采样项目信息

2.2 仿真总体构架

本次MATLAB仿真将分别对稳定状态下和大机动状态下两种情形进行仿真，并分别绘制出在这两种状态下，由陀螺仪、加速度计以及互补滤波算法解算出来的姿态角及航向角随时间的变化曲线图.然后，对稳定状态下的陀螺仪积分得到的姿态角随时间变化曲线进行分析，由于陀螺仪会发生漂移，所以预测误差很大.随后，对大机动状态下的加速计计算得到的姿态角随时间的变化曲线进行分析，由于加速度计在动态响应方面存在劣势，所以预测加速度计得到的结果偏差将比较大.最后，使用互补滤波算法求得姿态角随时间的变化曲线，并和前两中计算方法进行对比分析，如果PID参数选择准确，预测互补滤波效果会优于前两者.流程图解如图2所示.

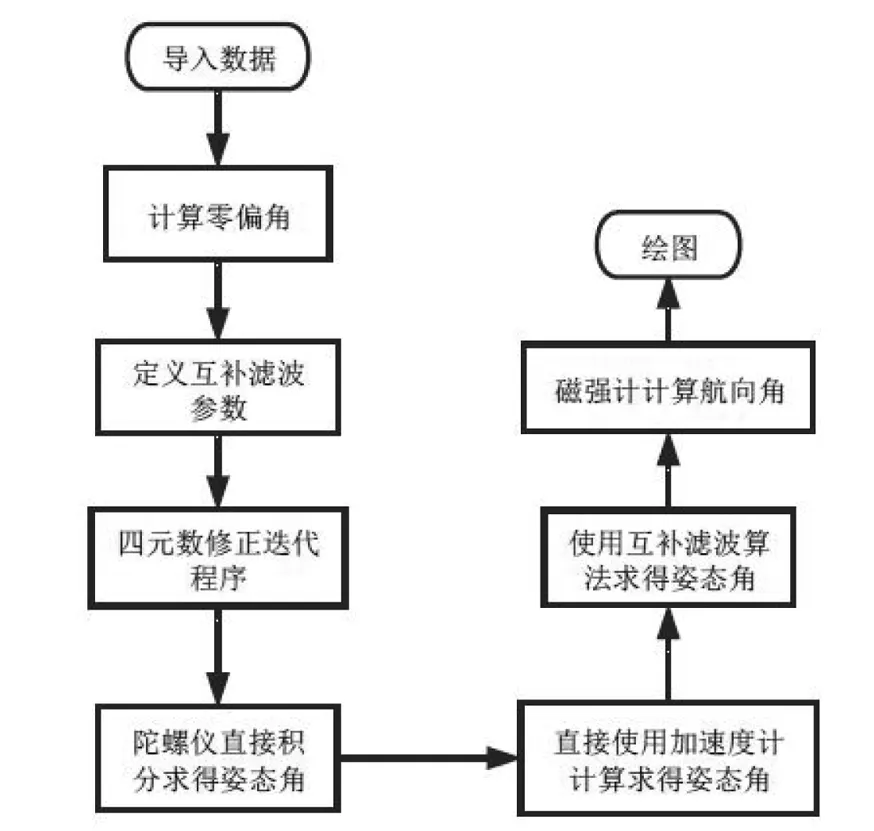
图2 仿真流程图

2.3 仿真实验

由于此次使用的MTI小型AHRS系统输出的数据有加速度计、陀螺仪、磁强计以及三个姿态角(Roll、Pitch、Yaw)，所以可将仿真得到的数据与MTI小型AHRS输出的原始姿态角数据进行对比分析.

(1)稳定状态下采集加速度计、陀螺仪，分别采用加速度计计算和四元数方法计算(陀螺仪积分)俯仰角、滚转角，得到结果如图3、图4所示.

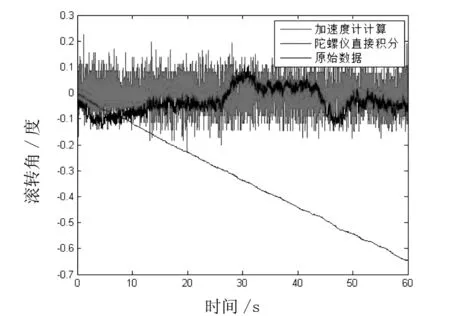
图3 滚转角变化

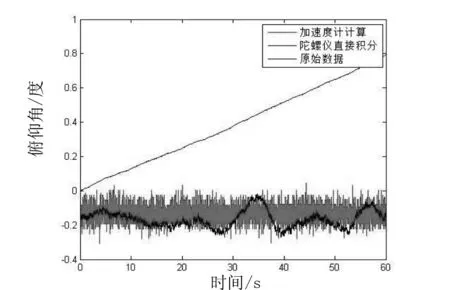
图4 俯仰角变化

从图3和图4中可以明显地看出，在四旋翼稳定飞行状态下，由于陀螺仪存在漂移的现象(即陀螺仪的误差会累积)，其在稳定的状态下所测得的滚转角和俯仰角，随着时间的增长，会越来越偏离真实值.因此，如果没有其他修正的方法，得到姿态角误差只会越来越大.所以，直接采用陀螺仪数据积分所得到的姿态角结果是不准确的.

(2)大机动时，只使用加速度计测量计算的姿态角数据与原始数据对比如图5和图6所示.

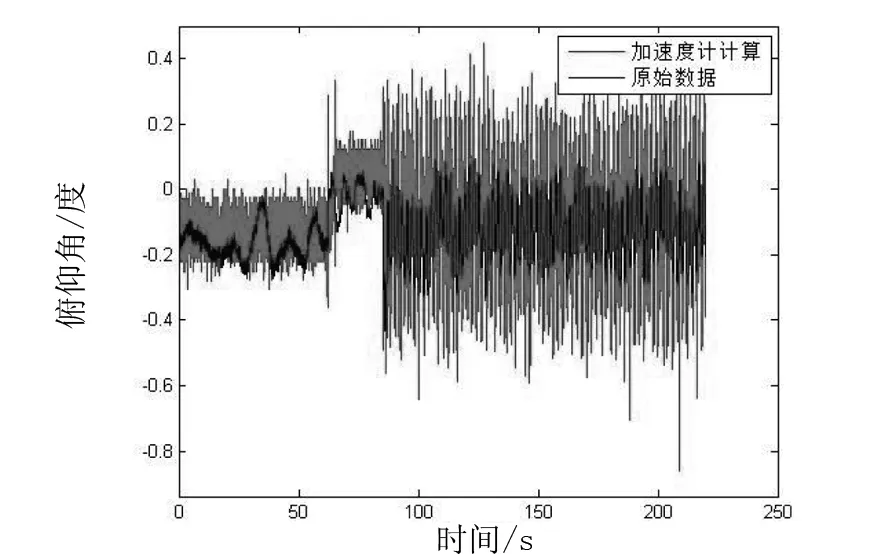
图5 俯仰角变化

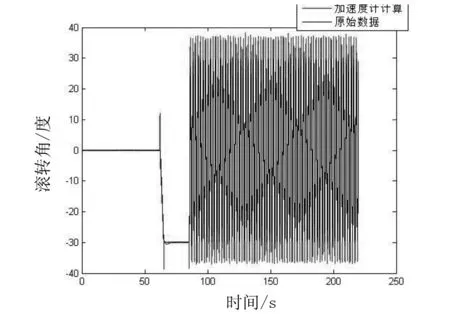
图6 滚转角变化

从图5和图6中可以看出，在80 s之后四旋翼做了较大的机动飞行，此时的加速度计计算的数据比原始数据大，即存在额外的加速度，致使测量误差更大，所以只使用加速度计测得的姿态角数据也是不准确的.

(3)同样的情况下，大机动时，采用加速度计数据和陀螺仪数据融合的方法(互补滤波)来进行仿真，所得到的姿态角变化曲线结果与加速度计直接计算的结果对比如图7、图8所示.为了达到对比的效果明确，将原始数据和加速度计计算的姿态角也放在图中.

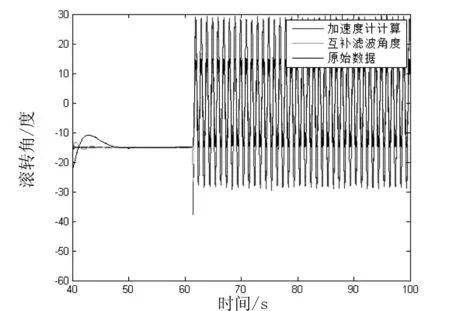
图7 滚转角变化

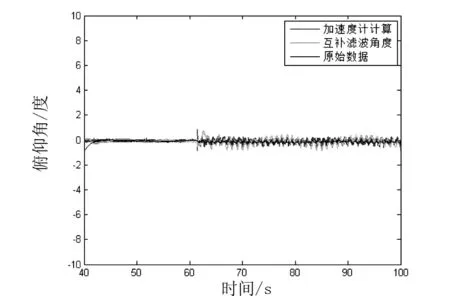
图8 俯仰角变化

显然，从图7和图8中可以看出，从63 s开始，四旋翼开始做大机动飞行，俯仰角大小几乎不变，而滚转角大小变化剧烈，说明四旋翼在进行较频繁的滚转机动飞行.而互补滤波器得到的滚转角几乎与MTI直接输出的原始数据重合，而加速度计由于其本身的动态劣势，使得测量误差较大.这证明互补滤波算法的优化作用是显而易见的，它能够综合陀螺仪和加速计的优点，使得测量精度更高，在大机动飞行时，动态响应更好.但是相比MTI小型AHRS直接输出的数据还有差距，考虑到这点，就需要进行一些对比.

为了更清楚的对比互补滤波算法所得到的姿态角的上下浮动情况与MIT系统输出的姿态角的数据的差别，取出部分仿真过程中的数据来进行计算，对各项都计算均方差，所得到结果见表2.

表 2 均方差对比

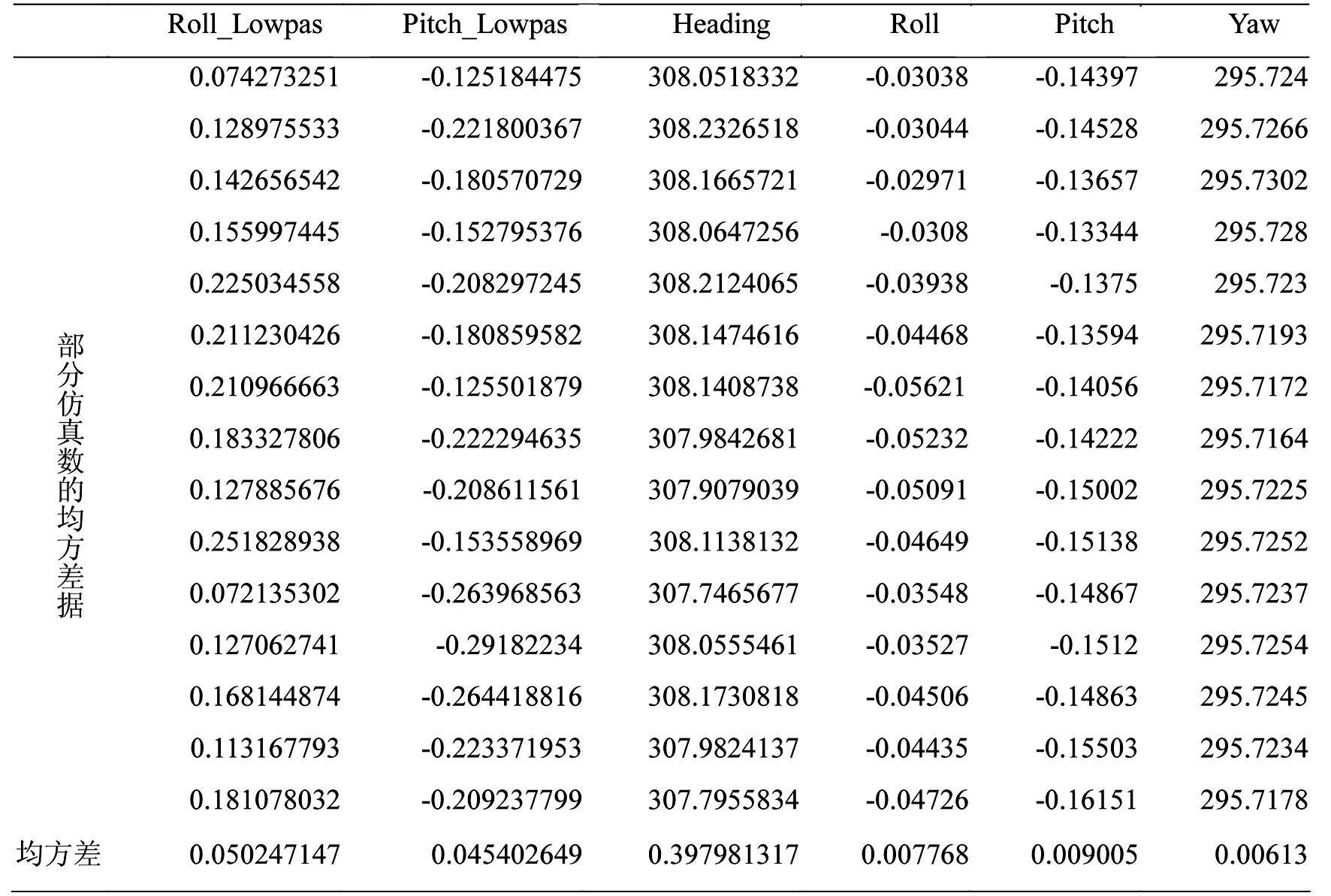
由表2可以看出，使用滤波算法所得到滚转角和俯仰角，以及用磁强计数据计算得到的偏航角数据的均方差都比MTI系统直接输出的三个姿态角的均方差大.虽然本文所采用的互补滤波算法相比于陀螺仪积分和加速度计直接计算有一定的优化效果，但是相比于MTI的数据来说，仍然不够稳定.这可能与MTI内部可能采用更为优化的卡尔曼滤波算法有关，在此后的研究中，将进一步深入研究.

(4)对于磁强计计算得到偏航角，与陀螺仪修正法得到的偏航角，该文只将其与原始数据进行对比，而不再将其进行互补滤波计算.不过程序中求解时对磁强计和陀螺仪所得结果均经行了修正.对比图如图9所示.

由图9可以看出，在63 s之后，由于四旋翼做大机动飞行，虽然只改变滚转角，但由于磁强计的动态响应较差，所以在那之后它所测得的数据也发生了较明显的变化.可以说明，磁强计的动态特性也不好.后续的研究中将进一步研究一些优化算法，会使磁强计得到的偏航角效果更好一些.

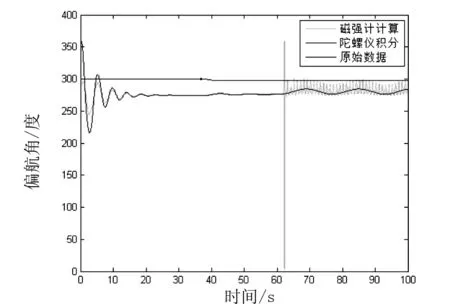
图9 偏航角变化

3 结束语

实验结果表明，在稳定状态下，相比直接使用陀螺仪数据积分计算得到的俯仰角和滚转角来说，加速度计计算得到俯仰角和滚转角还是比较稳定的，没有发生类似陀螺仪因漂移而产生的过大误差的情况.而在大机动飞行的时候，由于加速度计的动态响应很差，产生了额外加速度，导致其测出的数据有较大的误差.互补滤波算法综合了加速度计和陀螺仪的优点，所得到的结果更加接近原始数据，因此使用互补滤波算法进行姿态解算结果更加准确，工程应用方面亦可进行应用.

[1] 沈林成.无人机系统导论[M]. 北京：国防工业出版社，2014.9.

[2] 李荣冰,刘建业,曾庆化.基于MEMS技术的微型惯性导航系统发展状况[J].中国惯性技术学报,2004,12(6)：88-95.

[3] 时贵敏.基于MEMS传感技术的航姿系统算法研究[D].哈尔滨：哈尔滨工程大学工学硕士学位论文，2014.

[4] 徐鹏.某型无人机姿态航向参考系统的设计与实现[D].西安：西北工业大学硕士学位论文,2007.

[5] 郭晓鸿，杨忠，陈喆，杨成顺，龚华军，EKF和互补滤波器在飞行姿态确定中的应用[J],中国惯性技术学报,2011,30(11):56-60.

[6] 乔伟，刘鹏，黄艳辉. 微惯性单元姿态解算方法[J]，集成电路通讯,2011(3):36-40.

(责任编辑：季春阳)

The Simulation of Quadrotor Attitude Heading Based on MATLAB

Dai Jun, Liu Zhanhe, Wang Jing

(Zhengzhou University of Aeronautics)

In this paper, the simulation is analyzed on the information fusion algorithm based on the complementary filter and uses the actual experiments data of the inertial device from MTI small attitude heading

ystem. After comparing the results of attitude angle from the results of integral calculation of accelerometer and gyroscope and the results based on Complementary Filter, the optimization effect of the Complementary Filter theory applied in the attitude data measurement is analyzed.

Attitude Heading Reference; System; Complementary Filter; MTI

2016-02-09

*河南省科技厅(162102210237)；航空科学基金(2014ZA55001)；河南省教育厅(15A590001)

TP249

A

1000-5617(2016)02-0060-05