GARCH模型下我国商业银行同业拆借利率风险度量

余欣泉，曾小利

(福建师范大学经济学院，福建 福州 350117)



GARCH模型下我国商业银行同业拆借利率风险度量

余欣泉，曾小利

(福建师范大学经济学院，福建 福州 350117)

在利率市场化的大背景下，基于Shibor的统计数据，采用VaR方法，利用GARCH模型度量我国商业银行在同业拆借时所面临的隔夜拆借利率风险值与隔周拆借利率风险值。结果表明，GED分布条件下的GARCH(1，1)模型能够较好地拟合我国商业银行同业拆借利率的波动性。我国商业银行应坚定推行金融体制改革，同时不断完善SHIBOR运行机制及现有的度量模型去有效应对利率市场化带来的挑战。

商业银行；同业拆借利率；风险度量；GARCH模型

2013年7月20日，中国人民银行决定全面放开金融机构贷款利率管制，2014年以来存款利率也在不断放开。2015年，中国人民银行对存款利率进行了一序列改革：2015年5月11日，中国人民银行决定金融机构存款利率浮动区间的上限由存款基准利率的1.3倍调整为1.5倍； 2015年8月26日，中国人民银行决定放开一年期以上(不含一年期)定期存款的利率浮动上限；自2015年10月24日起，中国人民银行决定对商业银行和农村合作金融机构等不再设置存款利率浮动上限。经过这一序列利率市场化改革，利率将更多地受市场规律的影响，同时我国商业银行的利率风险管理问题也逐渐暴露出来。利率市场化改革毫无疑问会给我国商业银行带来一定程度的风险，尤其是在我国银行间同业拆借利率市场化之后， 随着交易量的激增，商业银行利率风险的表现更为突出，探寻一种行之有效的量化我国商业银行利率风险的方法已成为当务之急。

一、 文献综述

利率风险的准确度量是我国商业银行进行利率风险管理的前提。传统的利率敏感性缺口分析方法和持续缺口分析方法因其本身固有的缺陷已越来越不能满足现代商业银行利率风险度量的要求，而VaR模型在测度的范围、精度和工具等方面都较前两种方法为优，并且随着计算机和统计技术的不断发展，VaR方法运算量大和运算成本高的问题也得到了有效解决。

VaR模型源自马科维兹1952 年创立的基本均值一方差模型。Philippe Jorion于1997年第一次对VaR方法进行了详细的介绍和阐述。Kupiec 提出了检验Var 方法准确性的回溯检验方法，提出了基于失败次数似然比的检验。之后，随着研究的深入，学者们主要集中于研究VaR的计算方法。Shukur(2000)认为VaR能够用于根据风险来调整投资和交易的绩效，充当绩效评价的工具。Helmut(2001)认为VaR能够为交易者确定资金头寸的上限以及如何配置资本提供参考。Ricardo( 2006)、Beirne等( 2010)分别采用GARCH 模型对VaR进行预测。此后越来越多国家的金融当局视VaR模型为测量利率风险的有效工具。随着金融市场的发展，我国学者也开始对VaR方法进行了大量研究。戴国强、徐龙炳等人(2000)[1]通过对VaR方法在计算投资组合的潜在价值风险进行探讨，并列举了VaR方法对我国金融风险管理的四个意义，得出VaR方法适合运用到我国对商业银行的监管中去；王春峰( 2002)[2]指出，VaR模型中对于样本数列的正态性假设可以简化计算并且易于理解，但现实中的数据并不符合正态假设的理想分布。国内很多学者对同业拆借利率序列的分布情况进行了大量的研究。李成和马国校( 2007)[3]认为t 分布不适合描述我国银行间同业拆借利率序列的分布状况，广义误差分布(GED 分布)能较好地刻画我国银行间同业拆借利率序列的分布；王德全( 2009)[4]认为t分布和g分布下的模型能更好地捕捉我国银行间质押式回购市场利率序列的尖峰厚尾性；房小定、吕鹏(2013)[5]利用VaR 模型进行度量得出，EGARCH(1，2)-GED 分布能够较好地刻画Shibor对数收益率序列的分布结果。

二、 数据的选取与检验

同业拆借市场是我国率先完成利率市场化的市场，2007 年1 月4 日上海银行间同业拆放利率(Shibor)的正式推出，标志着我国货币市场基准利率培育工作的全面启动，作为我国打造的基准利率，其运行的效率和效果对于维护货币市场的稳定发展以及整个金融市场的发展都具有重要的意义。Shibor是由信用等级较高的银行组成报价团自主报出的人民币同业拆借利率确定的算术平均利率，可认为是剥离了信用升贴水后的利率。Shibor 的形成机制和运行机制与伦敦同业拆借利率Libor 具有较高的相似性，在每个交易日搜集各个银行的报价，通过算术平均计算后得出每一个品种的Shibor 值。本文基于Shibor上海银行间同业拆借利率，选取Shibor的O/N和1W数据作为样本[6]，数据期间为2012年1月4日到2016年2月25日，利用GARCH模型，然后在随机误差分布为t分布和GED 的假定下，采用对比分析的方法，选出拟合效果最优的模型对我国商业银行同业拆迁的利率风险进行VaR度量。

1.数据的处理

由于O/N数据和1W数据的序列波动非常剧烈，为了得到较为平稳的金融数据以便于分析，对Shibor的原始数据取对数，得到自然对数收益率[7]，公式表示为Rt=lnshiborrt-lnshiborrt-1，这样可以消除掉原始数据的自相关性，并使用Eviews 8对数据进行处理。

2.平稳性检验

为确定收益序列没有随机趋势或确定趋势，进而导致“伪回归”，首先对对数收益序列进行平稳性检验。Eviews里有多种平稳性检验的方法，本文选用ADF检验法。ADF检验法假设原始序列单位根，即非平稳的，如果检验结果接受原假设则说明原始序列是非平稳；反之就是平稳的，则需要对其进行一阶差分继续进行检验。检验结果如表1所示。

表1 ADF检验

其中R1表示银行隔夜拆借收益率，R7表示一周收益率。从表中可以看到，无论是在1%、5%或10%的临界水平下，对数收益率的ADF检验的T统计量都小于其置信水平下的临界值，因而拒绝原假设，选择备选假设，即该对数收益率序列不存在单位根，属于平稳序列[8]。

3.正态性检验

根据王春峰的研究可知，如果样本数据符合正态分布的特征，那么将会使得VaR模型非常简化并且易于理解，但是金融数据一般都体现出“尖峰厚尾”的非正态性特点，因此必须对原始数据进行正态性检验，检验方法通常有Quantile—Quantil图示法和Jarque—Bera检验法[9]，本文采用后一种方法进行检验，检验结果如图1、图2所示。

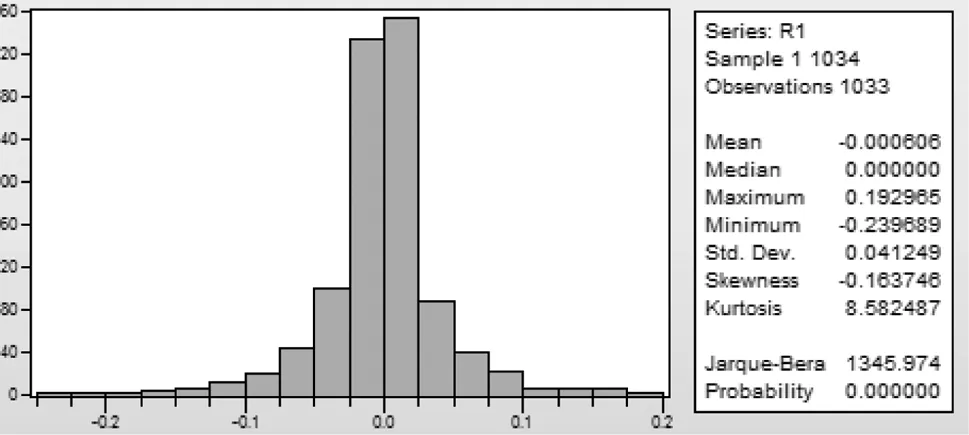
图1 R1序列的直方图

图2 R7序列的直方图

其中Skewness代表偏度，Kurtosis代表峰度，当样本序列服从正态分布时，S=0，K=3。Jarque—Bera检验法假设样本序列的分布和正态分布没有显著性差异，JB 统计量显示的P 值的意义是在JB 统计量超出原假设下观测值的情况下的概率，倘若概率比较小，就拒绝原假设，也就是说该序列是不服从正态分布的。从R1和R7序列的直方图中可以看到，原始序列的概率分布并不符合正态分布的“钟形”特征，其中SR1=—0.16，KR1=8.58；SR7=0.19，KR7=6.20，均超过正态分布的K=3，其凸起程度远远大于正态分布，呈现出尖峰形态，并且R1和R7的JB值分别为1345.9与448.1，都非常大，相应的概率都为0，表明在1%的显著性水平下可以拒绝原假设接受备选假设，所以样本数据的时间序列不服从正态分布。

4.自相关性检验

为有效避免“伪回归”结果的出现从而提高模型估计的准确度与可信性，必须判别回归方程的扰动项是否存在序列相关，所以进行自相关性检验。常用的序列相关的检验方法一般有先关图、DW统计量检验、序列相关的LM检验和Q统计量检验，本文采用相关图的检验方法。Q统计量检验法假设样本时间序列是非自相关的，如果Q统计量的概率值p大于给定的显著性水平，则接受原假设，即时间序列是非自相关的；如果概率值p小于给定的显著性水平，则拒绝原假设，即收益率序列是自相关的。

从Eviews中的序列直方图可以看到，R1序列的Q统计量概率都为0，而AC和PAC的值都不等于0且大多数的值都接近0，因此可以认为R1序列存在较弱的自相关。R7序列在滞后四阶后其Q统计量概率都变为0，并且AC和PAC的值都处于接近于0的数值，也可认为R7序列存在较弱的自相关。可以得出结论，样本数据序列存在较弱的自先关性，但是为了便于分析数据，假定对数收益率序列R几乎不存在自相关性，因此将均值方程设定为白噪声，方程为：R=u+εt[10]，其中u为收益率序列的均值，εt表示残差。

5.条件异方差性检验

在进行线性回归模型检测时，通常要求随机误差项是同方差的，但是在面对金融数据序列时，此假设往往是不成立的，因为金融序列的数据一般会表现出“波动聚集性”的特征，所以其随机误差项通常是不稳定的。在对金融时间序列进行建模时，应先判断其残差序列是否存在异方差性，即判断模型估计得到的残差序列是否存在ARCH效应。本文选用残差平方图检验法对ARCH效应进行检验。残差平方序列的相关图给出了残差平方序列直到任意指定的滞后长度k的自相关函数和偏自相关函数，并计算相应各期滞后阶数的Q统计量[11]。如果残差序列不存在ARCH效应，则残差在所有的滞后阶数上的自相关函数和偏自相关函数统计上都显著地不异于0，且其相应的Q 统计量也不显著；否则则说明残差序列存在ARCH效应。

从Eviews中得到的R1和R7的残差平方相关图中都可以看到其AC和PAC值都显著地不为0，并且在滞后了四阶后其Q统计量都大于50，而与Q统计量相伴随的概率值都为0，所以拒绝原假设，即银行同业拆借的对数收益率存在条件异方差现象，可以建立GARCH模型进行度量。

三、GARCH模型的建立

GARCH模型是一个针对金融数据所专门设定的回归模型，与普通回归模型不同之处在于它对随机误差项的方差进行了进一步的建模，特别适用于波动性的分析。而对于存在“尖峰厚尾”特征的金融数据[12]，GARCH模型能够进行很好的描述。通常低阶的GARCH模型就能够充分描述数据的集聚性，所以对于一般的GARCH(p，q)模型，先取p=1或2，q=1或2，然后再通过对比这些不同模型的AIC和SC值判断具体的p值和q值，从而选出最优的模型。对于GARCH(1，1)、GARCH(1，2)、GARCH(2，1)和GARCH(2，2)模型建立后的AIC和SC值比较后的结果如表2所示。

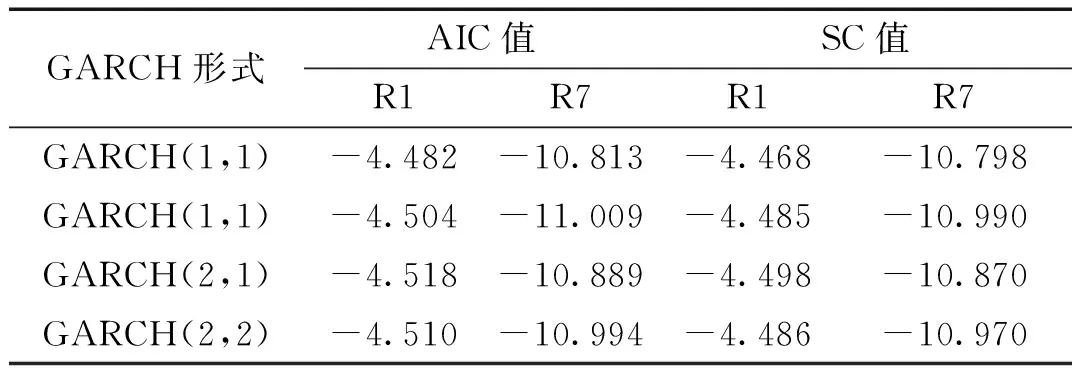
表2 R1和R7 GARCH模型的AIC值和SC值比较

由表2可以看到，R1序列和R7序列的GARCH(1，1)的AIC值和SC值最小，并且其各系数都通过了显著性检验，所以选用GARCH(1，1)模型，并通过ARCH—LM检验判断其ARCH效应是否已经被消除。结果如表3。

表3 R1和R7基于GRCH模型的ARCH-LM检验结果

从表3中可以看到，R1的F统计量为0.009951，其伴随的概率是0.9206，大于0.05，表明模型已经消除了条件异方差现象，得到的模型结果如下：

同时也可以得出R7的F统计量及其伴随的概率分别为0.0045109和0.8318，其概率值大于0.5，表明模型消除了条件异方差现象，因此可以得到R7序列的模型结果：

四、实证分析

1.模型分析

根据上文的分析，可知收益时间序列不符合正态分布的特征，表现出“尖峰厚尾”的特点，所以建立模型时不能使用模型系统默认的正态分布的假设，对残差分布作t分布和GED分布的假设，然后基于不同分布假设下的GARCH模型进行对比选出最优模型[13]。基于t分布和GED分布的GARCH(1,1)模型，利用Eviews得出结果如表4。

表4 R1基于t分布和GED分布的GARCH(1，1)的拟合结果

根据表4的计量结果，R1序列的拟合结果都是基于t分布的ARCH项，非对称项的系数都不显著，因此拟合效果都较差，而基于GED分布的ARCH项与非对称项系数都比较显著，模型的拟合结果较好。基于同样的方法分析R7序列也得出R7序列基于GED分布的ARCH项与非对称项系数都比较显著，因此选取基于GED分布的GARCH(1，1)模型对收益序列进行分析。

2.基于GED分布的GARCH(1，1)模型下的VaR计算

五、结论及建议

随着我国利率市场化改革进程的不断推进，传统的利率敏感性缺口度量模型因其本身固有的缺陷已经不能满足市场需求，必须立足于我国商业银行自身的特点选取更好的利率风险度量模型。GARCH模型对于那些具有“尖峰厚尾”特征的数据能够进行很好的描述。通过正态性检验得出结论，我国商业银行同业拆借的收益数据不符合通常的正态分布的特征，表现出“尖峰厚尾”的特征，并且具有集聚现象，可以通过GARCH模型来度量其面临的利率风险大小。

通过对不同分布条件下的GARCH模型的比较发现，广义误差分布(GED)条件下的GARCH模型对于度量我国商业银行同业拆借时所存在的利率风险具有更好的拟合度，并且滞后一阶的GARCH(1，1)模型的效果最好。GARCH能够很好地刻画我国商业银行在利率市场化的大金融背景下，在同业拆借时所面临的风险大小，隔夜拆借的VaR值是4.5%，隔周拆借时的VaR值为9.87%。我国商业银行在同业拆借时，必须通过制度和技术上的改进以降低甚至消除这些风险。

首先，从宏观视角来看，必须坚定不移地进行金融体制改革，同时全面进行利率市场化改革，使商业银行成为市场的主宰者，由市场决定利率的变化。利率的市场化改革使得存款利率的上限不断抬高，贷款利率的下限不断降低，银行的利润不断被压缩，提高了利率风险。我国商业银行必须采取一系列措施以有效应对利率市场化带来的挑战，大力发展不受利率影响的表外业务，同时加强实施差异化策略进而创造比较优势增加竞争力。我国商业银行体系还应努力培育一个以金融市场供求为基础，对其他利率的确定起到指导性作用和制约的基准利率。

其次，基准利率是我国利率市场化改革的重要组成部分，金融管理机构必须不断完善SHIBOR的运行机制。随着SHIBOR的正式运行，我国培育货币市场的基准利率的进程已拉开序幕，但是SHIBOR本身固有的交易结构不均衡问题也逐渐表现出来，只能生成有效的短期利率曲线，而无法形成长期有效的报价系统。我国商业银行应大力发展中长端交易市场，提高金融债券、企业债券、公司债券等债券市场的交易规模，从而形成连续、稳定的中长端交易数据，进而形成连续稳定的长期利率曲线。

最后，我国商业银行在度量其风险时应优化现有的风险度量模型。随着利率市场化的不断加深，我国同业拆借市场所面临的外部环境也越来越复杂，传统的利率度量模型的弊端也随之不断暴露，因此需要不断改进已有的模型。GARCH模型能够较好的拟合我国商业银行同业拆借利率的波动性，同时VaR方法可以比较准确地度量出我国同业拆借利率的风险值，并且越来越受到国际金融体系的重视。我国商业银行应从自身的性质和特点出发，不断展现出其特有的优势，提高使用VaR方法的精确性。

[1]戴国强，徐龙炳，陆蓉.国际汇率波动的非线性探索及其政策意义[J].国际金融研究，1999，(10):9-15.

[2]王春峰，万海辉，李刚.基于MCMC的金融市场风险VaR的估计[J].管理科学学报，2000，(2):55-64.

[3]李成，马国校.Var模型在我国银行同业拆借市场中的应用研究[J].金融研究，2007，(5):62-76.

[4]王德全.外汇风险度量——基于GARCH类模型及VaR方法[J].南方金融，2009，(8):11-15.

[5]房小定，吕鹏.基于GARCH模型的上海同业拆借利率风险度量[J].西北电子科技大学学报，2013，(4):18-25.[6]宿玉海，王美伶.我国商业银行隔夜拆借利率风险值(VaR)度量[J].财政金融研究，2015，(6):106-112.[7]何晓光，黄德权.基于ARMA——GARCH类模型的SHIBOR的VaR比较[J].经济管理研究，2014，(4):38-43.[8]何有世，赵金伟.基于CVaR的上海银行间同业拆放利率风险度量[J].财会月刊，2011，(5):45-48.

[9]孙德山.基于GARCH模型的深证综合指数收益率波动性研究[J].辽宁师范大学学报，2015，(4):447-451.

[10]张恒，吴可.基于GARCH模型的人民币汇率波段动态特征研究[J].经济数学，2015，(4):94-98.

[11]徐炜，黄炎龙.GARCH模型与VaR的度量研究[J].数量经济技术经济研究，2008，(1):121-131.

[12]严伟祥，张杰.基于GARCH——VaR模型的对冲基金市场风险度量研究[J].经济管理研究，2013，(5):78-83.[13]李成，马国校.VaR模型在我国银行同业拆借市场中的应用研究[J].金融研究，2007，(5):62-77.

[14]杨夫立.基于GARCH 模型的证券投资基金VaR计算与实证研究[J].经济问题，2012，(6):87-90.

(责任编辑：杨成平)

The Risk Measurement of China’s Commercial Bank Interbank Offered Rate under GARCH Model

YU Xin-quan, ZENG Xiao-li

(School of Economics, Fujian Normal University, Fuzhou 350117, China)

Under the environment of interest rate liberalization, the paper uses Shibor data, VaR method and GARCH model to measure the risk for China’s commercial bank interbank offered rate. The results show that GARCH (1,1) model under the GED distribution can well fit the volatility of the interbank offered rate in China’s commercial banks. China’s commercial bank should carry out financial system reform, and improve SHIBOR mechanism and existing measurement model to meet the challenges of interest rate liberalization.

commercial bank; interbank offered rate; risk measurement; GARCH model

2016-5-28

余欣泉(1990-)，男，江西景德镇人，研究生。研究方向：经济计量分析与预测。

F064.1

A

1008-4940(2016)05-0010-06