辫子群的q-组合式

胡红梅

(华东师范大学数学系,上海200241)

辫子群的q-组合式

胡红梅

(华东师范大学数学系,上海200241)

从标准R-矩阵和适当选取的相互对偶的辫子群出发,作者在［1］中利用双重玻色化定理刻画了ABCD型量子包络代数Uq(g)的递归构造.本文详细刻画在这些递归构造中,辫子群的生成元在更高一秩的新量子群中的表达式,它们是关于单根向量的q-组合式形式.

R-矩阵;递归构造;q-组合式;辫子群;FRT-型生成元

0 引言

Majid在拟三角霍普夫代数的表示构成的辫子张量范畴的框架下重新理解了Rad ford的双积,建立了玻色化理论［2-5］.之后,Majid又在文章［6］中发展了双重玻色化理论,这个理论不仅改进了FRT-构造［7］,而且也将Drinfeld在文章［8］中建立的量子双重理论推广到由辫子群的一个弱拟三角对偶对所伴随的广义量子双重理论.双重玻色化理论是建立在由拟三角的霍普夫代数(H,R)的表示构成的辫子张量范畴中的.简略地来说,从两个相互对偶的辫子群出发,然后通过双重玻色化理论在张量空间上存在唯一的更大的新量子群结构,它由H通过附加的“正根”B和附加的“负根”扩张而成,其中两个玻色化都是这个新量子群的子霍普夫代数.特别地,从李代数g的根格Q和对偶根格Q∨出发,Majid建立了一个弱拟三角对偶对,然后把量子群的正负部分Uq(n±)看成“Cartan”部分H的表示范畴里的相互对偶的辫子群,利用上面的双重玻色化理论实现了文章［9］中的Uq(g).另一方面,当H是经典型量子包络代数Uq(g)时,依据弱拟三角对偶对,通过Oq(G)的余表示范畴中相互对偶的辫子(余)向量代数来得到Uq(g)的表示范畴中相互对偶的辫子群,作者证实了这个新的量子群是更高一秩的量子包络代数,且给出了具体的递归构造过程［1］.本文中作者将通过这些构造来分别具体刻画每种构造中的辫子群V(R′,R)和的生成元在新量子群中的表达式,它们都是关于新量子群的单根向量的q-组合式形式.

1 ABCD型量子包络代数的递归构造

首先简述一下在文章［1］中关于ABCD型量子包络代数的双重玻色化的递归构造.引言中出现的是扩张的量子包络代数［10］,它可以被粗略地理解成由形如的群像元所伴随的更大的量子包络代数.Oq(G)是相应类型的李群的坐标代数的量子化,它是FRT-双代数A(R)的商霍普夫代数［7］.在文章［6］中证明了这两个霍普夫代数构成弱拟三角对偶对,对偶关系式是,其中R是相应的标准R-矩阵,具体定义将在下面给出.λ被称为量子群正规化常数,称为的FRT-型生成元.Majid在文章［11］中讨论A(R)的余表示构成的辫子范畴时引入了如下的相互对偶的辫子向量代数V(R′,R)和辫子余向量代数.

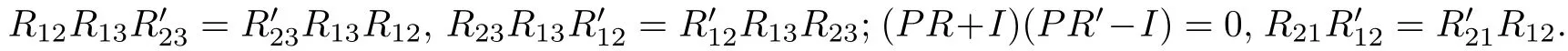
定义1.1［11］设R是任意一个可逆的R-矩阵,R′是另一个可逆矩阵,且满足:这里的P是置换矩阵.V(R′,R)由1和{ei|i=1,···,n}生成,且满足关系左余作用使得它是辫子范畴A(R)M中的辫子群,称为辫子向量代数,其辫子群的结构是

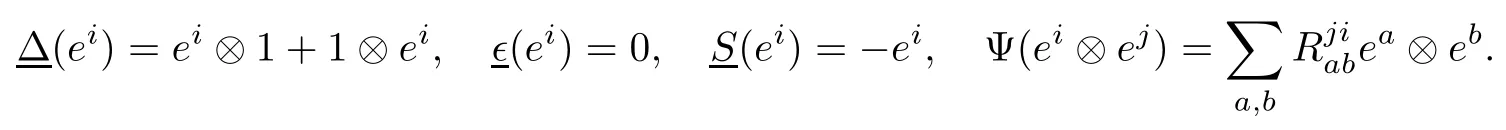
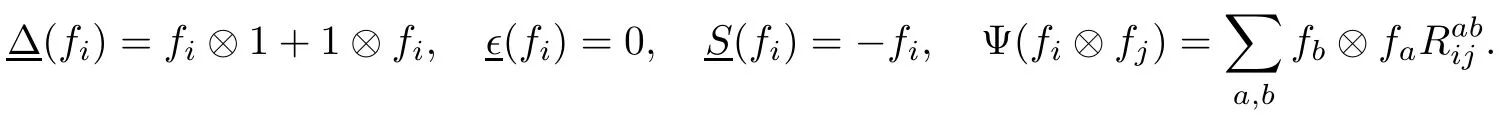
定理1.2［1］设R是ABCD型标准R-矩阵.当R是A-型时,选取R′=q-2R;当R是BCD-型时,选取R′=RPR-(∈q∈-N+1+q2)R+(∈q∈-N+3+1)P(BD-型对应的∈=1,C-型对应的∈=-1).其中当N是偶数时,令N=2n;当N是奇数时,令N=2n+1.双重玻色化构造得到的新量子群有如下的交叉关系式和余积

(1)A-型

B,C,D型的向量表示的量子群正规化常数λ=q-1.

(2)B-型

将辫子群中的元素e2n+1,f2n+1,及矩阵m+中的元素分别同构等同为新增加的单根向量En+1,Fn+1以及群像元Kn+1,那么利用双重玻色化构造得到的新的量子群同构于量子包络代数Uq(so2n+3).

(3)C-型

将辫子群中的e2n,f2n,以及元素同构等同为新的单根向量En+1,Fn+1以及群像元Kn+1,则就同构于由所伴随的量子包络代数Uq(sp2n+2).

(4)D-型

将辫子群中的e2n,f2n,以及元素同构等同为新的单根向量En+1,Fn+1以及群像元Kn+1,则就同构于由所伴随的量子包络代数Uq(so2n+2).

下面我们就来探究上面定理的每种递归构造中的辫子向量代数和辫子余向量代数V(R′,R),中的生成元在新量子群中的表达式.由定义1.1可知辫子向量代数和辫子余向量代数V(R′,R),是由一对矩阵数据(R,R′)决定的.不同的R,R′矩阵对应不同的辫子群.

2 辫子群的q-组合式

我们将利用新量子群在定理1.2中的交叉关系式(1)和(2)来探究辫子群在这些新量子群中的表达式.首先我们来考虑上面的A型的递归构造中的辫子群在新量子群中的表达式.在接下来的内容中我们用的标准R-矩阵同有些文献(例如［9］,［10］)中的标准R-矩阵是P°*°P的关系.我们也定义一个记号［x,y］q:=xy-qyx.

A-型的标准R-矩阵中的每个元素的表达式为

命题2.1定理1.2的(1)中将辫子群中的生成元en+1,fn+1同构等同为新量子群中的单根向量En+1,Fn+1后,则辫子群和V(R′,R)中其余生成元在新量子群中的表达式是如下的q-组合式形式.

从这些表达式可以观察到

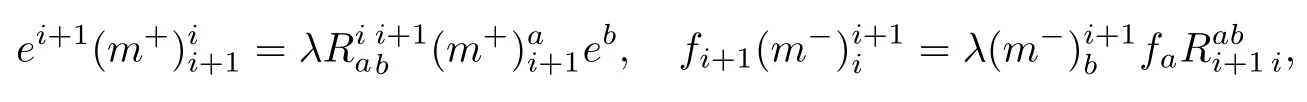
然后再根据R-矩阵中的元素的取值(4),可得

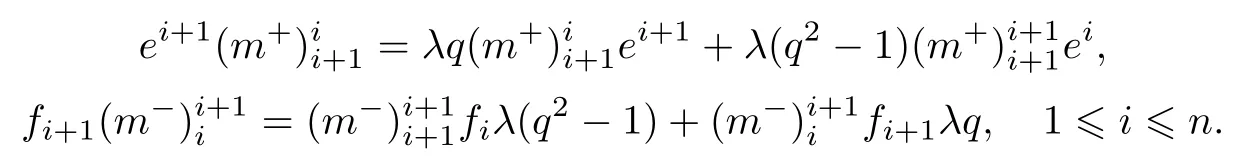
然后将关系式(7)代入,可得

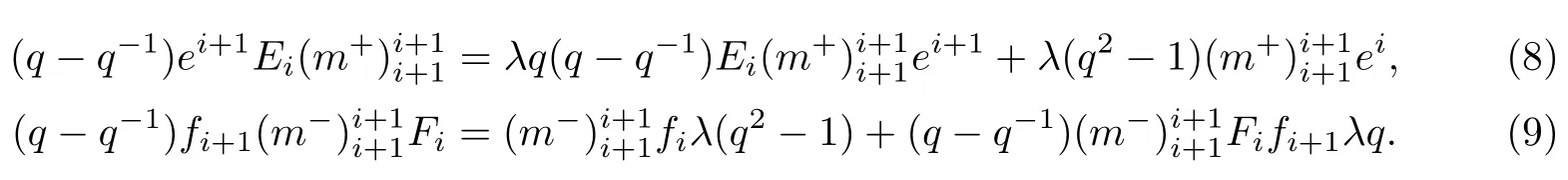
同样再由新量子群中的交叉关系可得

将这些关系式分别代入(8),(9)中,可得

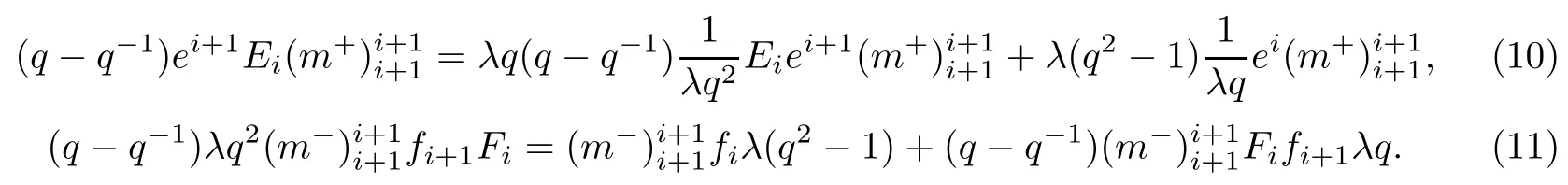
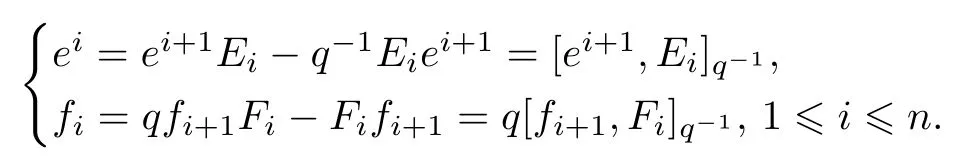
从而得到了关系式(5)和(6),命题得证.

接下来我们将分别考虑BCD型的递归构造中辫子群的生成元在新量子群中的表达式.首先给出BCD型的标准R-矩阵中的每一个元素的取值表达式

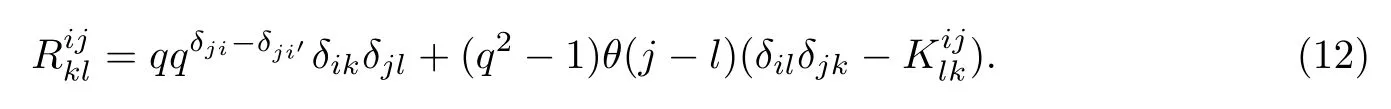
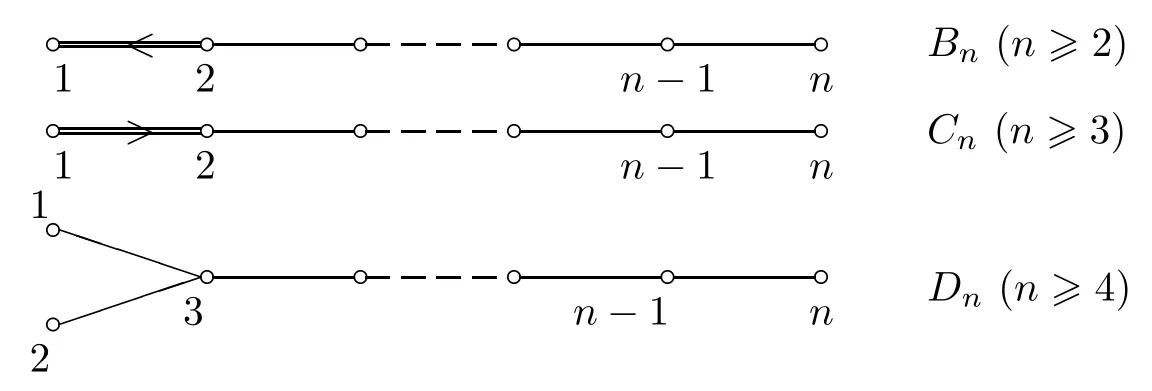
对应B-型,∈=∈1=···=∈2n+1=1.并且当i＜n+1时,;当i=n+1时, ρn+1=0;当i＞n+1时,.根据(12)式可知B-型的标准R-矩阵中一些位置元素的具体取值.首先根据可知,如果i+j/=2n+2,或者l+k/=2n+2,则.因此对于任意的i,j,我们有

命题2.2定理1.2的(2)中将辫子群中的生成元e2n+1,f2n+1同构等同为新量子群Uq(so2n+3)中的单根向量En+1,Fn+1后,则辫子群和V(R′,R)中其余生成元在新量子群中的表达式是如下的q-组合式形式.

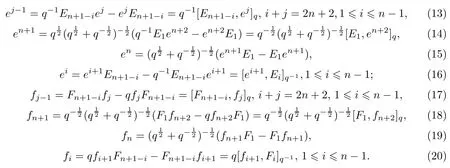
当1≤i≤n-1,i+j=2n+2时,则n+3≤j≤2n+1⇔n+2≤j-1≤2n.依据新量子群中的交叉关系和上面的R-矩阵的取值可得

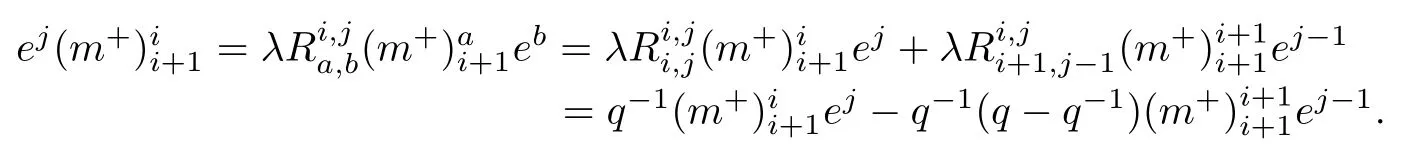
然后再根据新量子群中如下两个交叉关系式

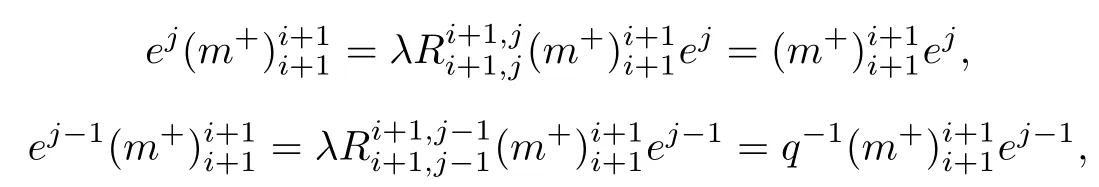
则关系式(21)就变为

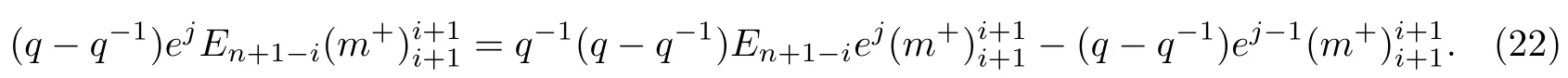
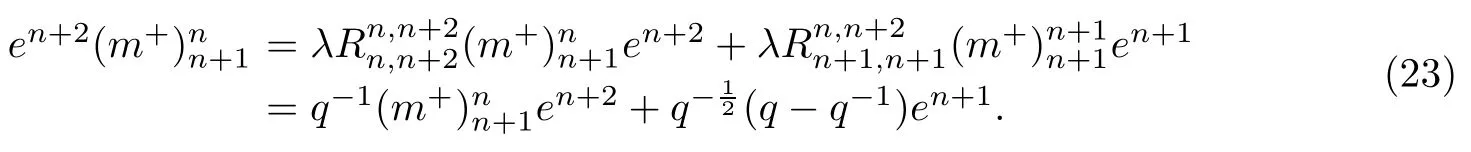
命题2.3定理1.2的(3)中将辫子群中的生成元e2n,f2n同构等同为新量子群Uq(sp2n+2)中的单根向量En+1,Fn+1后,则辫子向量余代数和辫子向量代数V(R′,R)中其余生成元在新量子群中的表达式是如下的q-组合式形式.

证明对应Uq(sp2n)的向量表示,我们需要的中的FRT-型生成元以及一些关系式在文章［1］中已经给出,下面我们先罗列出这些元素.

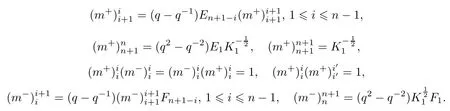
当i+j=2n+1,1≤i≤n-1时,则n+2≤j≤2n⇔n+1≤j-1≤2n-1.同理依据新量子群中的交叉关系式以及R-矩阵中元素的取值,证明的具体过程类似.下面我们主要给出依据的交叉关系式以及得到的结论.根据R-矩阵的取值,我们可以得到下面这些具体的交叉关系等式:

依据这些等式,可证得(27)式.同时为了证明等式(28),我们主要依据下面的交叉关系式:

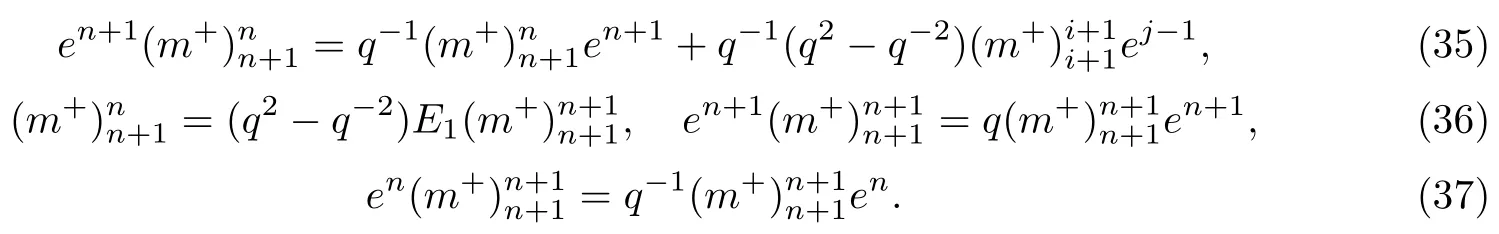
而另一方面,我们再根据R-矩阵中元素的取值,以及双重玻色化递归构造中新量子群的交叉关系式,可得到下面的等式:

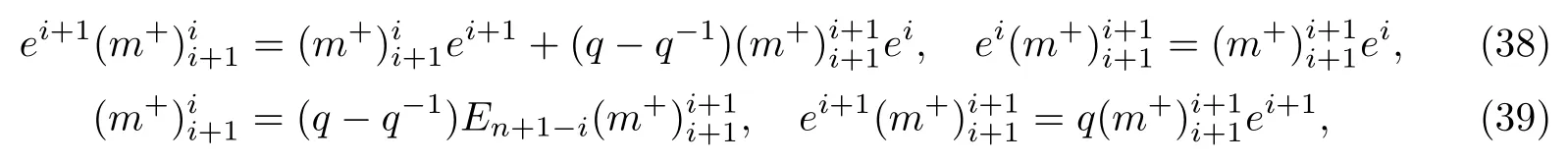
再依据这些等式可得证(29)式.而表达式(30)-(32)可类似得证.

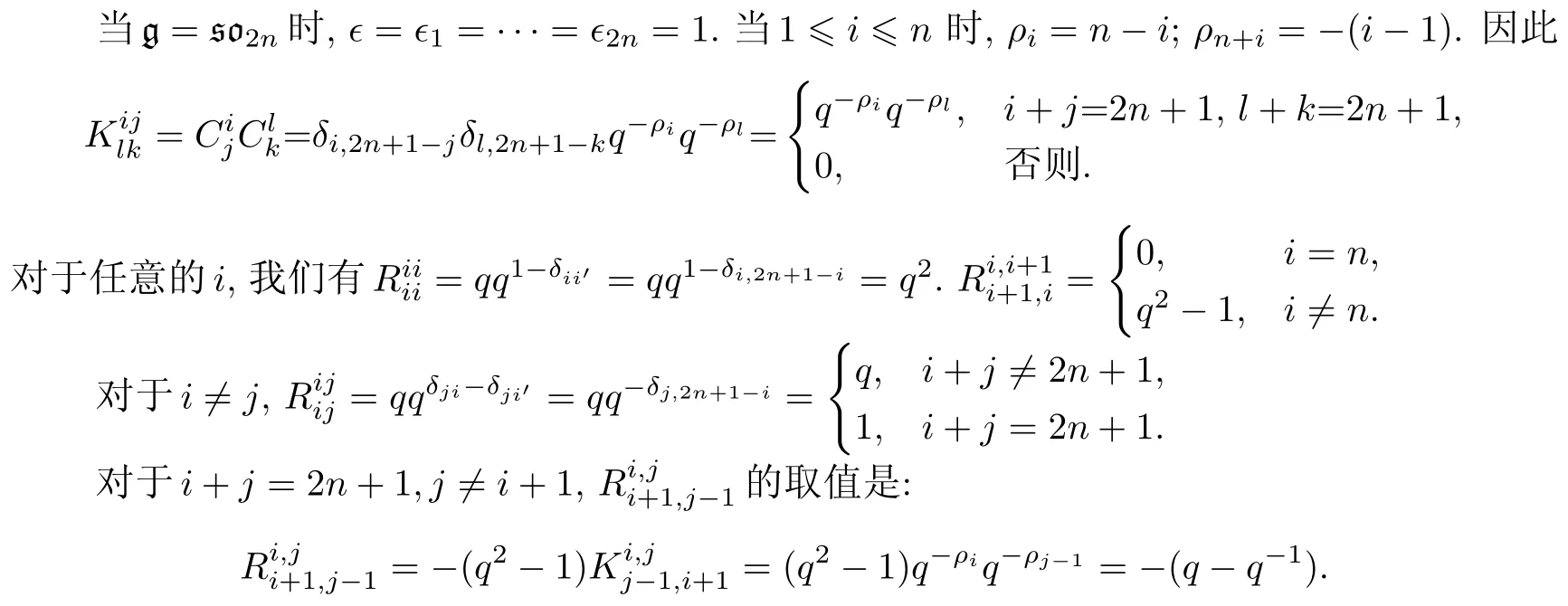
命题2.4定理1.2的(4)中将辫子群中的生成元e2n,f2n同构等同为新量子群Uq(so2n+2)中的单根向量En+1,Fn+1后,则辫子群和V(R′,R)中其余生成元在新量子群中的表达式是如下的q-组合式形式.

证明对应Uq(so2n)的向量表示,我们需要的中的FRT-型生成元以及一些关系式同样在文章［1］中已经得到了,罗列如下:

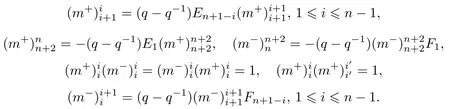
当i+j=2n+1,1≤i≤n-1时,则n+2≤j≤2n⇔n+1≤j-1≤2n-1.同理依据新量子群中的交叉关系式以及R-矩阵中元素的取值,我们得到如下的关系式:

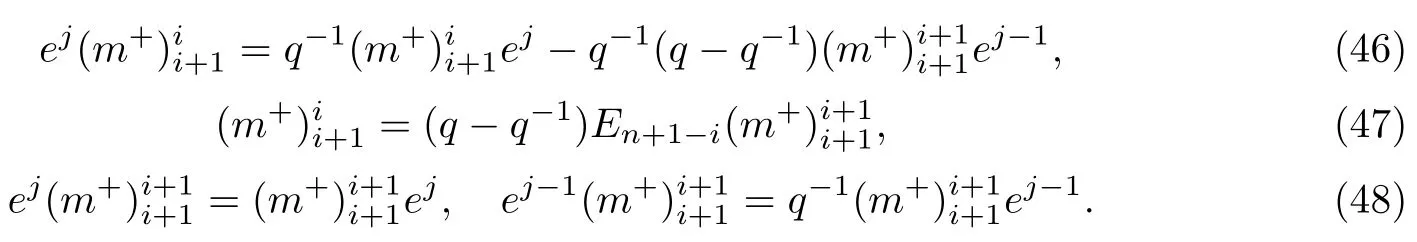
然后依据这些关系式,可证明得到关系式(40).为了得到en的表达式,我们考虑下面的交叉关系式,其中用到的取值.

因此我们得到下面的这些关系式:

依据这些等式,可以得证关系式(41).而另一方面,我们再依据R-矩阵的取值,又得到下面的关系式:

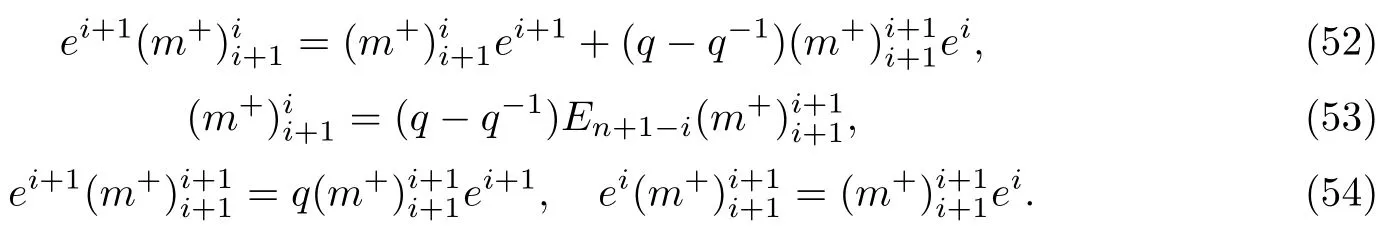
它们可以用来得到关系式(42).而表达式(43)-(45)可类似得证.

［1］HU H M,HU N H.Double-bosonization and Majid’s conjecture,(I):rank-induction of ABCD［J/OL］.Journal of Mathematics and physics,2015,56(111702);http://dx.doi.org/10.1063/1.4935205.

［2］RADFORD D.Hopf algebras With projection［J］.Journal of Algebra,1985,92(2):322-347.

［3］RADFORD D,TOW BER J.Yetter-Drin feld categories associated to an arbitrary bialgebra［J］.Journal of pure and Appl Algebra,1993,87(3):259-279.

［4］MAJID S.Cross products by b raided groups and boson ization［J］.Journal of Algebra,1994,163(1):165-190.

［5］MAJID S.Some comments on bosonization and biproducts［J］.Czech Journal of physics,1997,47(2):151-171.

［6］MAJID S.Double-bosonization of braided group s and the construction of Uq(g)［J］.Math proceedings Cambridge philos Society,1999,125(1):151-192.

［7］FADDEEV L D,RESHETIKHIN N Y,TAKHTA JAN L A.Quantization of Lie groups and Lie Algebras［J］. Leningrad Mathematics J,1990,1(1):193-225.

［8］DRINFELD V G.Quantum group s［C］//proceedings of the International Congress of Mathematicians.American Mathematics Society,1987,1(2):798-820.

［9］LUSZT IG G.Introduction to Quantum Groups［M］.Cam b ridge,MA:Birkhäuser,1993.

［10］K LIM YK A,SCHMÜDGEN K.Quantum groups and their representations［M］.Berlin:Sp ringer-Verlag,1997.

［11］MAJID S.B raided momentum in the q-poincare group.Journal of Mathematics physics［J］.1993,34(5):2045-2058.

(责任编辑林磊)

The q-commutators of b raided groups

HU Hong-mei
(Department of Mathematics,East China Normal University,Shanghai 200241,China)

With the standard R-matrices and suitably chosen a pair of dual braided groups,the authors gave the rank-inductive constructions of Uq(g)for the ABCD series via the double-bosonization theory in［1］.This paper described exp licitly the expressions for the generators of braided groups in the new higher rank-one quantum groups in these constructions,which are the q-commutators With the simple root vectors.These q-commutators are very important to the structure of new quantum groups.

R-matrix;rank-inductive construction;q-commutator;braided group; FRT-generator

O152.2

A

10.3969/j.issn.1000-5641.2016.01.002

1000-5641(2016)01-0009-10

2015-04

国家自然科学基金(11271131)

胡红梅,女,博士研究生,研究方向为量子群及其表示理论.E-mail:hmhu0124@126.com.