用《高等数学》微积分工具解决高中物理问题

叶晓文

（山东东平明湖中学高三卓越班 271500）

用《高等数学》微积分工具解决高中物理问题

叶晓文

（山东东平明湖中学高三卓越班 271500）

本文章针对《高等数学》中的微积分工具对高中物理问题进行分析，采用过程语言对物理过程进行描述，帮助同学更好地理解数学物理问题，为解决高中物理难题提供一种新方法。

一般来讲，我们在高中所接触到的物理问题，都是从宏观上进行分析，列出数学方程式进行计算，最后得出数学答案，再转化为物理含义。往往在解题的过程中，忽略了物理学的内在含义。为了解决这个问题，本文采用《高等数学》中微积分的思想，对高中物理中的典型问题进行分析，达到从物理角度，利用数学工具，解决物理问题的目的。

下面，我们就力学中的有关问题对微积分的应用进行阐述：

一、解决变速直线运动位移问题

但是，这一种公式从表面上看无法与 物理过程相联系。在运动的过程中，物体的速度是连续变化的，不应该用一个固定的公式来进行计算。这样会给学生理解物理过程带来很大的困难。又比如加速度是不断变化时，这时候又必须重新推导公式，下面我们尝试用微积分来进行求解。

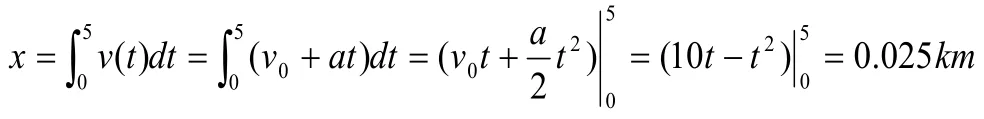
二、解决变力做功问题

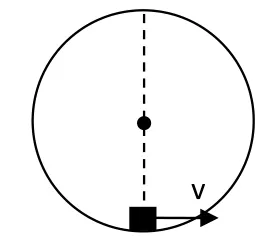
例2：如图所示，质量为m的物体以恒定速率v沿半径为R的竖直圆轨道运动，已知物体与竖直圆轨道间的摩擦因数为μ，求物体从轨道最低点运动到最高点的过程中，摩擦力做了多少功。

普通解析：物体沿竖直圆轨道从最低点匀速率运动到最高点的过程中，在不同位置与圆环间的正压力不同，故而摩擦力为一变力，本题不能简单的用 sFW .= 来求。

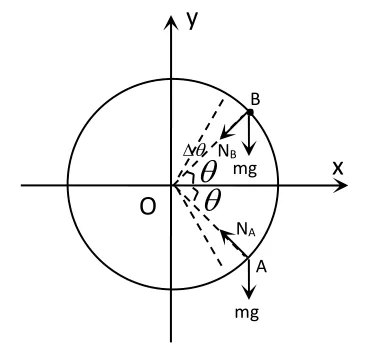
可由圆轨道的对称性，在圆轨道水平直径上、下各取两对称位置设与水平直径的夹角为在的足够短圆弧上可看作直线，且摩擦力可视为恒力，则在两点附近的内，摩擦力所做的功之和可表示为：

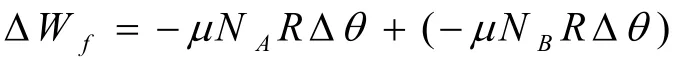
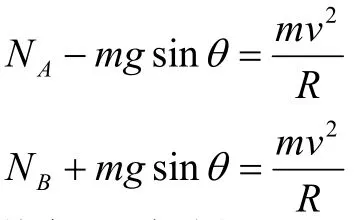
综合以上各式得 ：

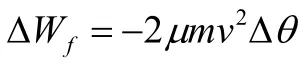
帮摩擦力对车所做的功：

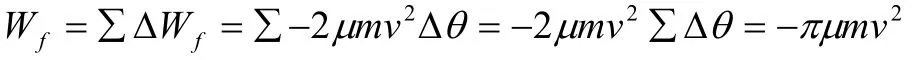
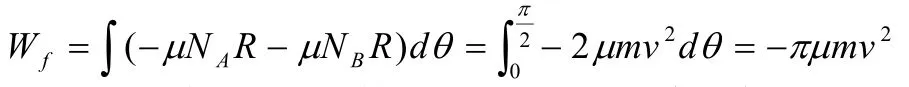
这题是一个复杂的变力做功问题，利用公式直接求功是难以办到的。利用微积分思想，把物体的运动无限细分，在每一份位移微元内，力的变化量很小，可以忽略这种微小变化，认为物体在恒力作用下的运动；接下来把所有位移仙的功相加，即“无限求和”，则总的功就可以知道。

三、微分的应用

下面我们从代数上考察物理量的变化率：

例3.若某质点做直线运动，其位移与时间的函数关系为上s=3t+2t2，试求其t时刻的速度的表达式。（所有物理量都用国际制单位，以下同）

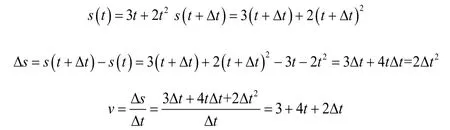
在高中物理中还有很多例子，比如我们讲过的瞬时速度，瞬时加速度、感应电动势、引力势能等都用到了微积分思想，所有这些例子都有它的共性。作为大学知识在高中的应用，虽然微积分高中不要求，但他的思想无不贯穿整个高中物理。“微积分思想”丰富了我们处理问题的手段，拓展了我们的思维。我们在学习的时候，要学会这种研究问题的思想方法，只有这样，在紧张的学习中，我们才能做到事半功倍，并可以解决一些复杂的物理问题。

[1] 高等数学，同济大学出版社，[M]，2007.4

[2] 高一物理必修一，人民教育出版社，[M]，