基于投影的直觉模糊群决策专家权重确定方法

孟俊娜,于利爽,刘炳胜

(天津大学管理与经济学部,天津300072)

基于投影的直觉模糊群决策专家权重确定方法

孟俊娜,于利爽,刘炳胜

(天津大学管理与经济学部,天津300072)

文章针对方案属性值为直觉模糊数的群决策问题,提出了一种基于投影的专家权重确定方法。该方法按照投影分析的基本思想,给出了确定直觉模糊环境下群决策专家权重的计算步骤。其核心是计算每个专家的隶属度矩阵在群体隶属度矩阵上的投影和非隶属度矩阵在群体非隶属度矩阵上的投影,进而利用领导者的偏好度求出专家个体决策矩阵与群体决策矩阵的相似度,最终确定每个专家的权重。最后给出的算例表明了该方法的可行性和有效性。

群决策;直觉模糊数;投影;专家权重

0 引言

Zadeh[1]于1965年提出了模糊集理论,该理论的核心思想是把取值仅为0或1的特征函数扩展到可在单位闭区间[0,1]中任意取值的隶属函数。由于模糊集的隶属函数值仅是一个单一的值,它并不能同时表示支持、反对和犹豫的程度,因而Atanassov[2]将仅考虑隶属度的Zadeh的传统模糊集拓展为考虑隶属度、非隶属度和犹豫度的直觉模糊集。直觉模糊集比传统的模糊集在处理模糊性和不确定性等方面更具灵活性和实用性,因此有关直觉模糊集理论的研究引起了学者们的广泛关注[3～8],并已应用于群决策和模式识别等领域。

目前,对于直觉模糊环境下的群决策专家权重确定问题的研究较少。文献[5]利用专家个体评价结果与群体评价结果的偏差最小化以及专家个体评价结果之间的偏差最小化,建立两个非线性规划模型确定专家的权重;文献[6]将专家矩阵集结为群体决策矩阵,利用专家矩阵和群体决策矩阵的相似度确定专家权重。文献[7]通过直觉模糊集的交叉熵和熵分别确定专家的权重,并利用组合加权法确定专家的最终权重。现有的直觉模糊环境下专家定权的研究多直接考虑专家个体决策矩阵和群体决策矩阵的关系,忽略了专家个体的隶属度矩阵和群体隶属度矩阵、非隶属度矩阵和群体非隶属度矩阵间的关系。基于此,本文以传统投影法的基本理论为基础,通过计算专家个体的隶属度矩阵在群体隶属度矩阵上的投影和非隶属度矩阵在群体非隶属度矩阵上的投影,最终确定直觉模糊群决策的专家权重。

1 预备知识

1.1 直觉模糊集和直觉模糊数

Atanassov在文献[2]中将Zadeh的模糊集扩展为直觉模糊集,考虑了隶属度、非隶属度和犹豫度三个方面的信息,因而能更细腻地刻画客观世界的模糊性本质。

定义1[2]:设X是一个非空集合,则称A=｛x,μA(x), vA(x)|x∈X}为直觉模糊集,其中μA(x)和vA(x)分别表示X中元素X属于A的隶属度和非隶属度,即μA:X→[0,1], vA:X→［0,1］,且满足0≤μA(x)+vA(x)≤1。此外,πA(x)= 1一μA(x)一vA(x)表示X中的元素X属于A的犹豫度。

定义2[9]:称a=(μa,va)为直觉模糊数,其中μα∈[0,1],vα∈[0,1],0≤μα+vα≤1。

定义3[10]:设αj=(μαj,vαj)(j=1,2,…,n)为一组直觉模糊数,且设IFWA:Θn→Θ,若

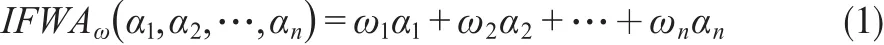
则称IFWA为直觉模糊加权平均算子。

其中ω=(ω1,ω2,…,ωn)T为αj(j=1,2,…,n)的权重向量,

定义4[10]:设αj=(μαj,vαj)(j=1,2,…,n)为一组直觉模糊数,则由IFWA算子得到的集成值也是直觉模糊数,且

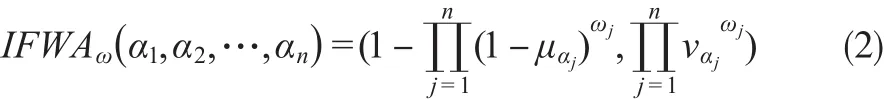
其中ω=(ω1,ω2,…,ωn)T为αj(j=1,2,…,n)的权重向量,ωj∈［0,1］(j=1,2,…,n),且

定义5[11,12]:对任一直觉模糊数α=(μα,vα),定义s(α)=μα一vα为a的得分函数,h(α)=μα+vα为a的精确函数。

定义6[10]:对于直觉模糊数α1=(μα1,vα1)和α2=(μα2,vα2), s(α1)=μα1一vα1和s(α2)=μα2一vα2分别为a1和a2的得分函数,h(α1)=μα1+vα1和h(α2)=μα2+vα2分别为a1和a2的精确函数,则:

(1)若s(α1)＜s(α2),则α1＜α2;

(2)若s(α1)=s(α2),则

①若h(α1)=h(α2),则α1=α2;②若h(α1)＜h(α2),则α1＜α2;③若h(α1)＞h(α2),则α1＞α2。

1.2 投影法

定义7[13,14]:设α=(α1,α2,…,αn)和β=(β1,β2,…,βn)是两个n维向量,定义:

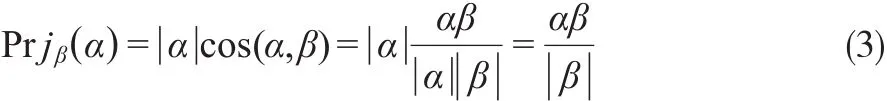
一般来说,Pr jβ(α)的值越大,表示向量a越接近于向量β。

与向量间的投影类似,Yue[15]给出了矩阵间的投影式。

为矩阵A在矩阵B上的投影。类似地,Pr jB(A)的值越大,表示矩阵A越接近于矩阵B。

2 基于投影的直觉模糊群决策专家权重确定过程

对于直觉模糊环境下的多属性群决策问题来说,假设有m个可行方案A1,A2,…,Am,n个评价属性G1,G2,…,Gn和t个决策专家E1,E2,…,Et。决策专家Ek对可行方案Ai在评价属性Gj下的决策值为直觉模糊数则专家Ek(k=1,2,…,t)的直觉模糊决策矩阵为:

下面给出基于投影的直觉模糊群决策专家权重确定方法的具体计算步骤。

步骤1:将专家Ek(k=1,2,…,t)的直觉模糊决策矩阵Xk分为隶属度矩阵和非隶属度矩阵

步骤2:确定所有专家的群体决策矩阵X*。

这里,取所有专家对每个方案每个属性决策意见的均值为群体决策。因此,有:

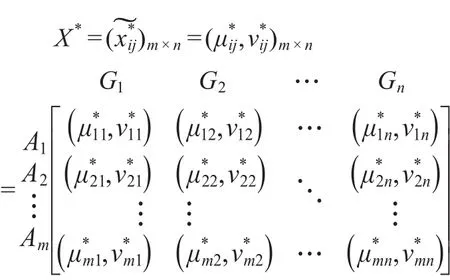
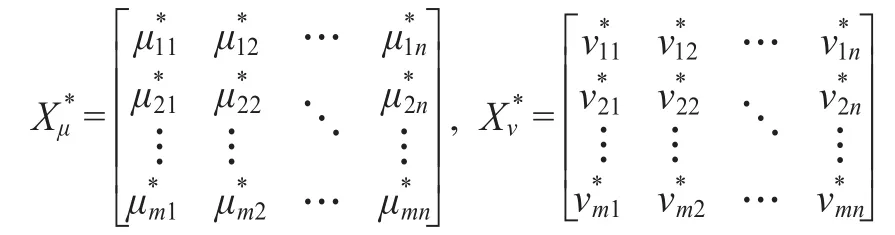
步骤3:将群体决策矩阵X*分为隶属度矩阵和非隶属度矩阵

式中：Te表示驱动电动机的的额定转矩(N·m)；ne表示电动机额定转速(r/min)；Tmax表示电动机的最大转矩(N·m)，过载系数λ，一般取2～3。

这里用专家决策矩阵在群体矩阵上的投影来衡量每个专家的评价值和群体值的相似程度。考虑到每个专家的决策矩阵和群体决策矩阵均包括隶属度矩阵和非隶属度矩阵,因此考虑两类投影关系:每个专家的隶属度矩阵在群体隶属度矩阵上的投影和每个专家的非隶属度矩阵在群体非隶属度矩阵上的投影。

步骤4:计算专家Ek(k=1,2,…,t)的隶属度矩阵在群体隶属度矩阵上的投影和专家的非隶属度矩阵在群体非隶属度矩阵上的投影。

由式(4)可以分别计算出:

①专家Ek(k=1,2,…,t)的隶属度矩阵在群体隶属度矩阵X*μ上的投影:

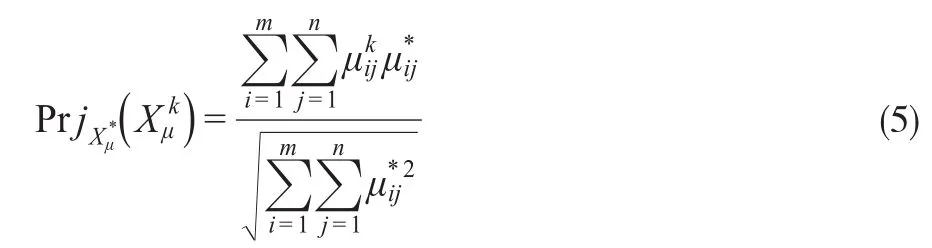
②专家Ek(k=1,2,…,t)的非隶属度矩阵在群体非隶属度矩阵上的投影:

步骤5:计算专家Ek(k=1,2,…,t)的决策矩阵Xk与群体决策矩阵X*的相似度。

一个专家的决策矩阵越相似于群体决策矩阵,那么这个专家的评价信息是重要的,应被赋予一个较大的权重。反之,一个专家的决策矩阵与群体决策矩阵差异较大,那么这个专家的评价信息是不重要的,因而应被赋予一个较小的权重。定义:

为专家Ek的决策矩阵Xk与群体决策矩阵X*的相似度。其中,定义θ∈［］0,1为偏好度,是一个给定值,表示领导者对隶属度矩阵信息的偏好程度。如θ=0.7表示领导者更偏好隶属度矩阵给出的信息。

步骤6:计算专家Ek(k=1,2,…,t)的权重值。

对Ek(θ)(k=1,2,…,t)进行归一化处理。有:

那么专家Ek的权重值为:

基于上面给出的专家权重确定方法,可以进行直觉模糊群决策。利用已确定的专家权重和式(2)可以得到每个方案的评价值,利用定义5和定义6可以对方案进行比较排序,最终确定最优方案。

3 算例

某一食品生产企业为其加工过程中的某原料在全国范围内寻找最优供应商。现在有5个供应商A1,A2,…,A5可供选择,该企业邀请来自各领域的4位专家E1,E2,…,E4利用5个决策属性对这5个供应商进行评估:G1为原料的价格; G2为原料的质量;G3为供应商的信誉;G4为供应商品质控制能力;G5为原料供应渠道的畅通性。专家Ek(k=1,…,4)利用直觉模糊数评估供应商Ai(i=1,2,…,5)在决策属性Gj(j=1,2,…,5)下的特征。专家Ek(k=1,…,4)评估结果表1至表4所示的直觉模糊决策矩阵Xk。

表1 专家E1的直觉模糊决策矩阵X1

表2 专家E2的直觉模糊决策矩阵X2

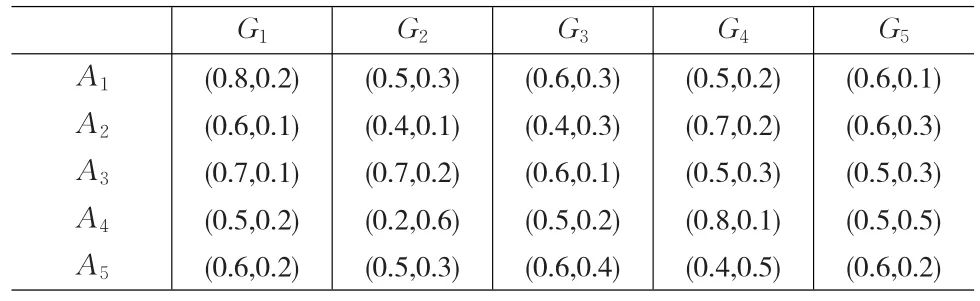
表3 专家E3的直觉模糊决策矩阵X3

表4 专家E4的直觉模糊决策矩阵X4

步骤1:将专家Ek(k=1,…,4)的直觉模糊决策矩阵Xk分为隶属度矩阵和非隶属度矩阵

由于篇幅限制,下面仅具体列出专家E1的隶属度矩阵和非隶属度矩阵

步骤2:确定所有专家的群体决策矩阵X*:

步骤3:将群体决策矩阵X*分为隶属度矩阵和非隶属度矩阵

步骤4:利用式(5)和式(6)可以得到专家Ek(k=1,…,4)的隶属度矩阵在群体隶属度矩阵上的投影和专家的非隶属度矩阵在群体非隶属度矩阵上的投影:

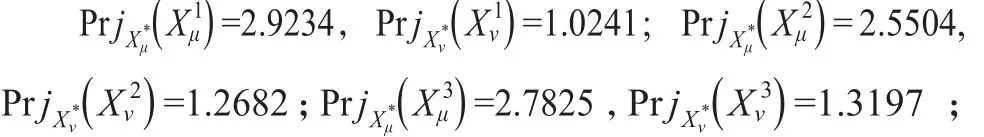
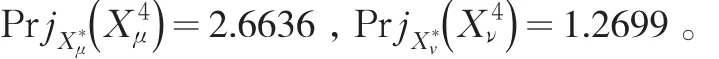
步骤5:计算专家Ek(k=1,…,4)的决策矩阵Xk与群体决策矩阵X*的相似度Ek()θ:

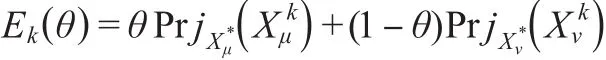
这里,取领导者的偏好度θ=0.7。则有:

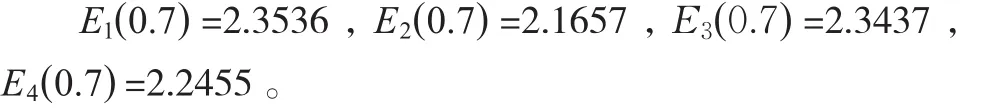
步骤6:计算专家Ek(k=1,2,…,t)的权重值。

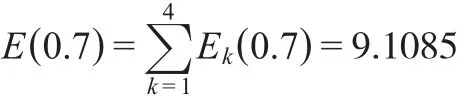
那么专家Ek的权重值为:

因此,4位专家E1,E2,…,E4的权重值分别为0.2584, 0.2378,0.2573,0.2465。

接下来,进行直觉模糊环境下的群决策。利用4位专家的权重和式(2),将他们对每个方案每个属性的直觉模糊矩阵集结为群体对每个方案每个属性的直觉模糊矩阵X:

设5个决策属性的权重分别为ρ=(0.2,0.15,0.2,0.3, 0.15)T。利用决策属性权重和式(2)可以集结群体直觉模糊矩阵X的每一行,从而得到每个供应商的直觉模糊评价值:

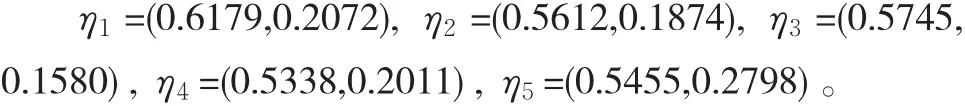
由定义5可得每个供应商的得分函数值:

依据供应商的得分函数值和定义6,可以得到各供应商的排序为:

因此,最优供应商为A3。

4 结束语

对于直觉模糊环境下的群决策问题,本文提出了基于投影的专家权重确定方法。该方法的核心是计算专家个体的隶属度矩阵在群体隶属度矩阵上的投影和专家个体的非隶属度矩阵在群体非隶属度矩阵上的投影,然后利用偏好度,求出每个专家的决策矩阵和群体决策矩阵的相似度,进而确定专家权重。本文的方法充分考虑并利用了专家个体和群体的隶属度矩阵和非隶属度矩阵的信息,提高了群决策的科学性和可靠性。这为直觉模糊群决策下确定专家权重提供了一种新的方法和思路。最后给出的算例分析表明该方法有效可行,在解决工程招标中的承包商选择、制造业中的供应商选择等存在不确定性因素的管理决策问题中简单实用。

[1]Zadeh LA.Fuzzy Sets[J].Information and Control,1965,(8).

[2]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems, 1986,(20).

[3]Zhang L y,Li T,Xu X H.Consensus Model for Multiple Criteria Group Decision Making Under Intuitionistic Fuzzy Environment[J]. Knowledge一Based Systems,2014,(57).

[4]w ei G w.Gray Relational Analysis Method for Intuitionistic Fuzzy Multiple Attribute Decision Making[J].Expert Systemswith Applications,2011,(38).

[5]Xu Z S,Cai X Q.Nonlinear Optimization Models for Multiple Attribute Group Decision Making w ith Intuitionistic Fuzzy Fnformation [J].International Journalof IntelligentSystems,2010,(25).

[6]Chen ZP,yangw.A New Multiple Attribute Group Decision Making Method in Intuitionistic Fuzzy Setting[J].Applied Mathematical Modelling,2011,(35).

[7]王晓杰,魏翠萍,郭婷婷.基于交叉熵和熵的直觉模糊多属性群决策专家权重的确定[J].曲阜师范大学学报,2011,(37).

[8]吴怀岗,张晴.基于直觉模糊集算子的多属性群决策方法[J].统计与决策,2010,(12).

[9]Xu ZS,yager RR.Some Geometric Aggregation Operators Based on Intuitionistic Fuzzy Sets[J].International JournalofGeneral Systems, 2006,(35).

[10]Xu Z S.Intuitionistic Fuzzy Aggregation Operators[J].IEEE Transactionson Fuzzy Systems,2007,(15).

[11]Chen SM,Tan JM.Handling Multicriteria Fuzzy Decision一making Problems Based on v ague Set Theory[J].Fuzzy Sets and Systems, 1994,(67).

[12]Hong D H,Choi C H.Multicriteria Fuzzy Decision一making Problems Based on vague Set Theory[J].Fuzzy Sets and Systems,2000, (114).

[13]王应明.多指标决策与评价的新方法——投影法[J].系统工程与电子技术,1999,21(3).

[14]徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.

[15]y ue Z L.Approach to Group Decision Making Based on Determining the w eights of Experts by Using Projection Method[J].Applied MathematicalModelling,2012,36(7).

(责任编辑/浩天)

C934

A

1002-6487(2016)20-0043-04

国家自然科学基金青年项目(71403181)

孟俊娜(1974—),女,山西运城人,博士,副教授,研究方向:项目管理、群决策分析与评价。于利爽(1989—),女,山东威海人,硕士研究生,研究方向:群决策分析与评价。刘炳胜(1979—),男,天津人,博士,副教授,研究方向:建筑业经济与管理、工程决策理论与方法。