空间分层数据无条件模型的改进及其估计

闵素芹,何晓群

(1.中国传媒大学理学院,北京100024;2.西京学院应用统计科学研究中心,西安710123)

空间分层数据无条件模型的改进及其估计

闵素芹1,何晓群2

(1.中国传媒大学理学院,北京100024;2.西京学院应用统计科学研究中心,西安710123)

抽样调查中得到的数据经常既包含个体信息又包含地理单元信息,形成以地区集聚的分层数据。空间分层数据中地理单元间往往具有空间依赖性,区别于传统的分层数据。分析空间分层数据时需要首先建立无条件模型用作初步分析。因此,在传统分层无条件模型中引入完全空间自回归模型来表达空间相关性,建立空间分层数据的无条件模型,并研究其估计方法,借助参数估计值可做模型选择。

无条件模型;空间依赖性;分层数据;EM算法

0 引言

社会科学研究中,样本往往来自不同的层次和单位,很多研究中采取的抽样方式为分层随机抽样,在这样的抽样设计下,个体的特征会产生集聚现象,由此得到的数据带来了分层的结构。比如,在抽样调查中,数据往往既包含个人信息,又有关于所在地区的信息。可以把这样的数据结构分层,个人信息看作第一层,地区作为第二层,即个人嵌套于地区。分层线性模型适用于处理此类数据,随着计算机技术水平的飞速发展,其估计方法的计算问题得以解决,近年来在社会科学和行为科学领域应用越来越广泛。

分层数据分析中经常将无条件模型用作初步分析,它可以提供两个层次中结果的变化信息。如Frenzel等(2007)[1]、Espelage等(2011)[2]、Simms(2014)[3]的研究中都首先运用无条件模型计算组内方差、组间方差、及组内相关系数(ICC),得出造成因变量的组间变异是不可忽略的,从而有必要进一步建立一般分层模型。Neupert等(2015)基于对51名60～96岁的老年人380天每天一次的追踪调查数据,运用分层模型研究应激预应对如何影响老年人的身体健康、记忆力减退等问题。重复测量的个体变化数据即纵向数据,将每一个人的多次测量视为嵌套于这个人。在利用分层线性模型时,层-1为重复观察模型,层-2为关注个体间差异的个人层次模型。研究中运用无条件模型分析了每天的应激预应对观测数据存在显著的个体内方差,结果表明每个人的应激预应对是动态变化的[4]。

在抽样调查中采用分层抽样设计时,层的划分常常按照行政区划进行,这样得到的数据既包含个体信息,又包含关于区域、城镇、市、省等的地理单元信息,就形成了以地区集聚的分层数据。空间分层数据因为地理单元间往往具有空间自相关性,区别于传统的分层数据。Ancelin也提到空间统计所面临的挑战时指出按一层观测值(如:空间单元层)进行的分析,不能提供低层(如个体行为)有用的信息[5]。由于传统分层模型假定地区间(组间)相互独立,而地理单元之间的空间相关性使得层-2模型残差的假设分布不再成立,从而估计出现问题。在分析空间分层数据时,也需要首先建立无条件模型。本文在分层模型中引入完全空间自回归模型来表达空间相关性,改进了传统分层数据的无条件模型,并研究其估计方法,依据参数估计值选择是否需要采用考虑空间效应的分层模型。

1 空间分层数据无条件模型的构建

无条件模型是最简单的分层线性模型,这种情况下层-1和层-2模型都不含自变量,模型为:

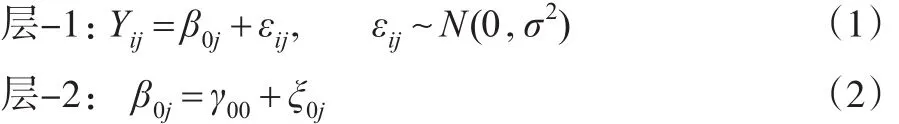
γ00代表总体中结果的总平均数,ξ0j为第j个组的随机效应,假定其均值为0,方差为τ00,σ2代表组内变化, τ00则捕获了组间变化。

对于空间分层数据,层-2模型残差分布的假设不再成立,残差的空间模式存在空间依赖性,引入能够描述空间自相关的项能有效的克服模型的缺陷。

在分析空间分层数据时,空间自相关反映为邻近地区β0间的依赖性,即地区1的β01,地区2的β02,…,地区J的β0J存在空间自相关。本文考虑在层-2模型中引入空间效应,空间效应用完全空间自回归模型来表达。此时,层-1模型与传统分层模型(1)一致,其中,yij是因变量, β0j是截距项,εij是随机误差项。

若以矩阵向量的方式表达,则式(1)为:

而空间分层数据中β0具有空间效应,此时,层-2模型为:

此模型为完全空间自相关模型,不包含解释变量。其中,ρ表示空间自相关系数,W表示J×J的空间权重矩阵,通常是二元对称矩阵,表达J个地理单元的空间邻近关系。

综上,带空间效应的两层模型的无条件模型表达为:

模型中,ρ＞0表示该地区被结果变量的值与其相似的地区所包围,即:结果变量高值的地区被其他相似的高值地区所包围,低值被低值所包围。另一方面,ρ＜0表示高值的地区被低值地区所包围。ρ=0则表示没有空间依赖,此时模型为普通的带随机效应的单因素方差分析模型。

2 无条件空间分层模型的最大似然估计

空间分层数据的无条件模型层-1无自变量,层-2为完全自回归模型。与传统两层模型相比,增加了空间效应表示部分,其中空间权重矩阵W是已知的,多了一个需要估计的参数ρ。要通过最大似然估计方法估计模型中的参数ρ，σ2，μ，τ。

下面给出期望最大化(EM)算法。期望最大化算法认为y是观测数据,ξ是缺失数据。因此,完整数据为(y，ξ),ρ，σ2，μ，τ是需要被估计的参数。

2.1 最大化步(M Step)

ξ是未知的层-2模型的误差项向量,其假设为:

因此,给定β0，σ2后y的条件分布为:

因E[y|ρ，σ2，μ，τ]=Uμ1J,V[y|ρ，σ2，μ，τ]=τU(I-ρW)-1(I-ρW)-1TUT+σ2IN,故,当ρ，σ2，μ，τ也为已知的情况下,y的条件分布为:

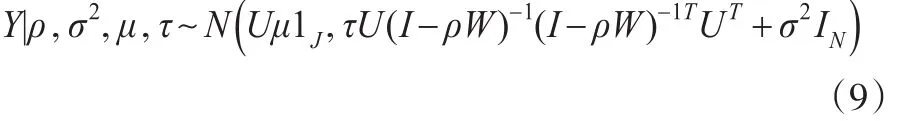
而且,cov(y，ξ)|ρ，σ2，μ，τ=cov(Uμ1J+U(I-ρW)-1ξ+ε，ξ)=E[(Uμ1J+U(I-ρW)-1ξ+ε-Uμ1J)ξT]=τU(I-ρW)-1

所以,y与ξ的联合分布为:

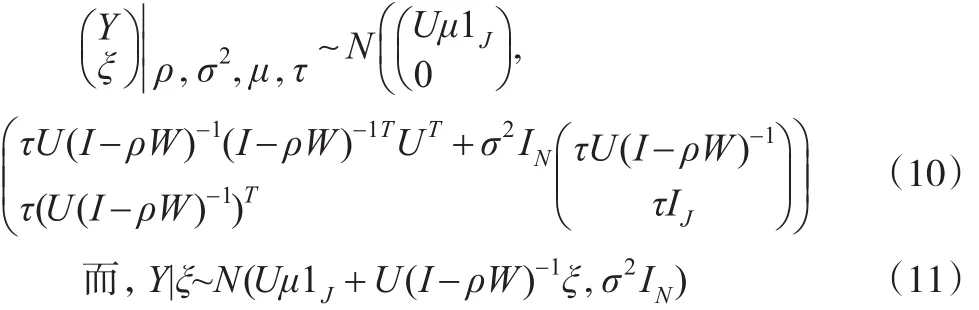
完整数据的似然函数取自然对数,得:

而,ln f(y，ξ|ρ，σ2，μ，τ)=ln l(ρ，σ2，μ，τ|y，ξ)对数似然函数ln l(ρ，σ2，μ，τ|y，ξ)分别对ρ，σ2，μ，τ偏微分,

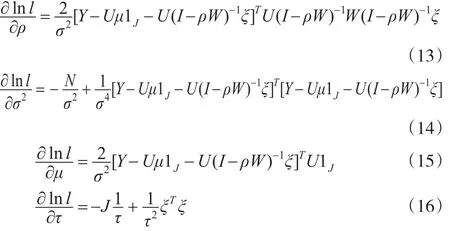
但是,无法给出ρ的显式表达。所以,考虑结合运用Fisher得分算法。得分向量为:

各分量由式(13)至式(15)给出。

Hessian矩阵为:

Fisher得分方法需要求二阶导数的期望矩阵,

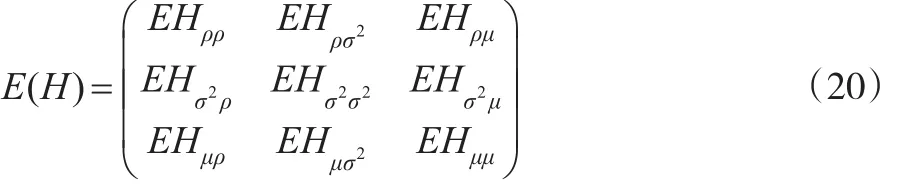
2.2 期望步

由式(10),根据正态分布剖分定理,y为已知的条件下ξ的条件分布的条件期望向量和条件方差协方差矩阵分别为:

将式(21)记为a,式(22)记为B。故,若y与ρ，σ2，μ，τ已知,由式(21)、(22),ξ的事后条件分布为:

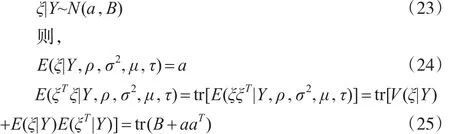
2.3 EM算法

(1)给出初始值ρ(0)，(σ2)(0)，μ(0)，τ(0);记ρ(k)，(σ2)(k)，μ(k)，τ(k)是第k+1次迭代开始时参数的估计值;

(2)估计完整数据的充分统计量:E(ξ|y，ρ，σ2，μ，τ)，E(ξTξ|y，ρ，σ2，μ，τ)

式(24)与式(25),这些期望值根据前一步迭代得到的ρ(k)，(σ2)(k)，μ(k)，τ(k)值求得;

(4)将新的参数估计值代入到步骤(2)中,重复上述步骤,M步和E步不断地迭代交互运算,直到所估计的参数值都很接近,或每次迭代运算的对数似然函数值变化很小,就达到收敛。可以通过计算每一步迭代的对数似然值来加以监测。

3 结论

根据参数ρ的值与其显著性可以反映邻近地区β0间的依赖性,根据σ2，τ的估计值,计算组内相关系数如果空间自回归系数ρ显著不为零,则认为空间自相关需要考虑,ICC≥0.059表示组间差异不可忽略[6]。此时,需要进一步建立空间分层模型进行后续分析。若ρ=0,ICC≥0.059则表示没有空间依赖性,但组间变异不可忽略,此时应选用传统分层线性模型进行后续分析。

[1]Frenzel A C,Pekrun R,Goetz T.Perceived Learning Environment and Students'Emotional Experiences:AMultilevel Analysis ofMathematics Classrooms[J].Learningand Instruction,2007,17(5).

[2]Espelage D,Green H,Polanin J,w illingness to Intervene in Bullying Episodes Among Middle School Students Individual and Peer一group Influences[J].The Journalof Early Adolescence,2011,(11).

[3]Simms K.Are Expectations About Health Care Universal?The International Evidence[J].Global Journal of Business and Social Science, 2014,1(10).

[4]NeupertSD,EnnisG E,Ramsey JL,etal.Solving Tomorrow's Problems Today?Daily Anticipatory Copingand Reactivity to Daily Stressors[J].The Journals of Gerontology Series B:Psychological Sciences and Social Sciences,2015,(3).

[5]Anselin L.The Future of Spatial Analysis in The Social Sciences[J]. Geographic Information Sciences,1999,5(2).

[6]温福星.阶层线性模型的原理与应用[M].北京:中国轻工业出版社,2009.

(责任编辑/亦民)

O212

A

1002-6487(2016)20-0016-03

北京高等学校“青年英才计划”项目(y ETP0611);中国传媒大学优秀中青年教师培养工程(y XJS2013330);中国传媒大学理工科规划项目(XNL1402)

闵素芹(1978—),女,山东青州人,博士,副教授,研究方向:统计模型理论与应用。何晓群(1954—),男,陕西西安人,教授,博士生导师,研究方向:应用数理统计。