怀化地区年最大日降雨量分布模型的确定及推算*

张　昆，陈章法，王起唤，肖　昀

（怀化市气象局，湖南怀化 418000）

怀化地区年最大日降雨量分布模型的确定及推算*

张昆，陈章法，王起唤，肖昀

（怀化市气象局，湖南怀化 418000）

采用怀化地区11个国家站1965～2014年的50年最大日降雨量资料，用-Ⅲ型分布﹑耿贝尔分布和对数正态分布3种概率分布模型，分别进行了拟合，选择拟合最好的分布模型，估算降雨极值的重现期及重现期值。结果表明，-Ⅲ型分布﹑耿贝尔分布﹑对数正态分布能较好地拟合年最大日降雨量的分布，在11个站的拟合中，有3个站用-Ⅲ型分布，2个站用耿贝尔分布，6个站用对数正态分布拟合最佳，且通过了显著性水平x2=0.05的拟合优度检验。

概率分布x2拟合优度检验重现期

沅江是洞庭湖水系的第二大河流，干流全长1033 km。其中，怀化市内447km，流域面积8.9163万km2。近年来，流域性洪水在沅江流域境内时有发生，给怀化地区经济社会发展带来了严重影响，特别是对沿岸城市﹑乡村造成了严重威胁，其产生与一些重现期长的最大降雨量有密切的关系。重现期很长的最大降雨量，如百年一遇的特大暴雨，虽然发生的概率很小，但若出现则可能造成毁灭性的灾害。因此，估算降雨极值的重现期，对防御洪涝及其次生灾害，有着十分现实的意义。从气象服务角度出发，估算降雨极值的重现期及重现期值，会给服务者和服务受众对于降水强度与历年相比有更直观的认识。

从一般数学意义上讲，随机变量的极值不稳定。但，在概率论的意义上，事件的极值可以是稳定的，对其极值的变化，可以进行概率预报。因此，应科学地解决实际中遇到的极值问题，必须对事件极值的概率分布理论，进行合理统计推断。文章运用Pearson-Ⅲ﹑耿贝尔分布﹑对数正态分布3种概率分布，分别拟合怀化地区11个站的年最大日降雨量，并进行x2拟合优度检验，从中选取最优拟合分布模型，估算降雨极值的重现期及重现期值。

1　资料和方法

文章选取怀化地区11个站1965～2014年的50年最大日降雨量数据，用Pearson-Ⅲ型分布﹑耿贝尔分布和对数正态分布3种概率分布模型分别进行了拟合，选择拟合最好的分布模型，从而估算降雨极值的重现期及重现期值。所选数据均经过质量控制及检验，可以确保准确性和精度误差。

1.1概念的提出

气候极值是相对某一统计时段而言。例如，某要素的极大值xp，如果其大于或等于xp的事件平均每N年出现1次，则称xp为N年一遇的极大值，它重现期就是N年。在要素年极值的原始序列{xi}中，xi大于或等于xp的发生概率。

P=P（x≥xp）=1/N

根据极大值的概率分布函数，可以推算出给定发生概率P对应的极大值xp，即重现期为N（=1/P）的极大值，这就是极大值的概率计算或概率分析。

1.2Pearson-Ⅲ分布

Pearson-Ⅲ分布具有广泛的概括和模拟能力，在气象上常用拟合年﹑月的最大风速和最大日降雨量等极值分布，其概率密度函数和保证率分布函数。

其中，参数x0为随机变量所能取的最小值，a为形状参数，β为尺度参数，Γ(α)是α的伽玛函数。用矩法估计可得3个参数的表达式。

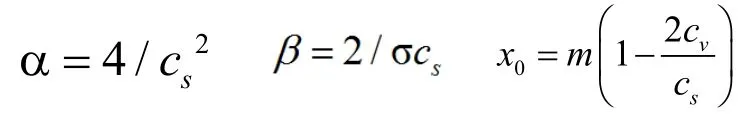
式中m为数学期望，σ为均方差，cs为偏态系数，cv为变差系数。

1.3耿贝尔分布

耿贝尔分布又称为第1型极值分布，其保证率函数。

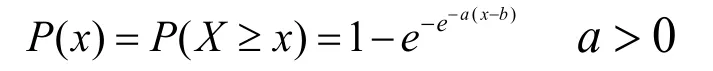
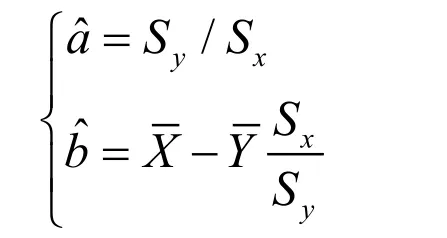
式中，xS﹑yS为标准差，为平均值。

1.4对数正态分布

假定极值变量的对数服从正态分布，设X为1极值变量，x为取值，它的对数lnYX=服从正态分布，即其中，ym和可估计。

1.5拟合优度检验

它反映了样本实际频数与理论频数的差异大小。其中，ni为观测频数，表示观测样本值落在区间(xi,xi+1)中的个数。若包含j个样本估计的参数，则统计量的自由度为v=k−j−1。给定信度a后，由查表得若χ2＜χ2，则认为样本服从该分布。具体步骤。

（1）根据年最大日降雨量样本的频数分布情况，将资料分成k个区间段。

（2）计算理论频数和实际频数。首先，计算频率Pi=P(xi+1)−P(xi)。其中i=1，2，…，k，样本量n与Pi的乘积nPi为理论频数。然后，统计每个区间内样本的实际频数ni。

（3）计算 χ2值。

（4）Pearson-Ⅲ分布有3个未知参数，自由度v=k−j−1=k-4；耿贝尔和对数正态分布有2个未知参数，自由度v=k−j−1=k-3。

1.6利用Excel计算各分布模型的累积分布函数及重现期值

利用Excel计算各分布模型的累积分布函数及重现期值（见表1）。

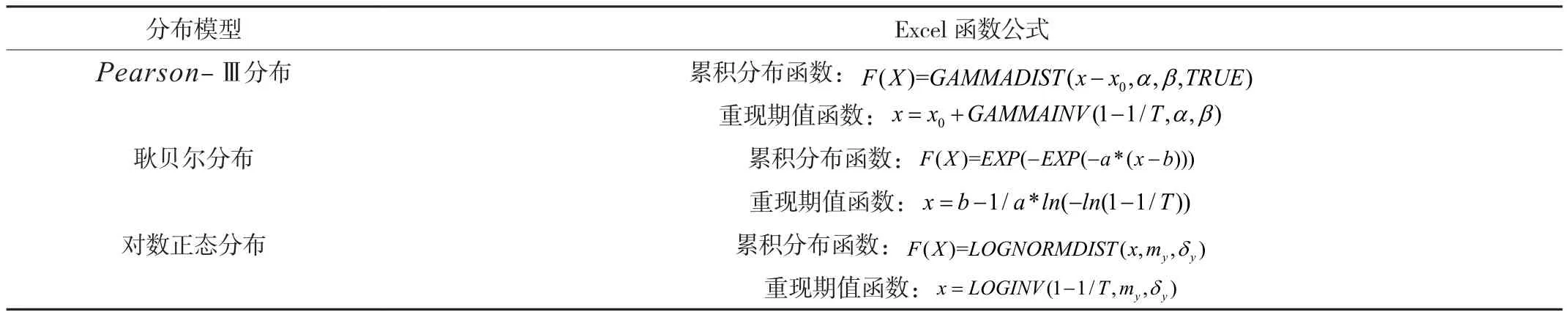
表1　利用Excel计算各分布模型的累积分布函数及重现期值

2　结果分析

2.1拟合优度检验

分别用Pearson-Ⅲ分布﹑耿贝尔分布和对数正态分布，对怀化地区11个站年最大日降雨量进行拟合，并进行了拟合优度检验。在通过检验的基础上，根据检验值的大小，选取最佳拟合分布，具体结果见表2。

表2　怀化地区各站年最大日降雨量拟合优度检验（a=0.05）

2.2重现期计算结果

针对不同的站点，选用最佳拟合分布模型，计算不同降雨量的重现期。具体结果见表3。

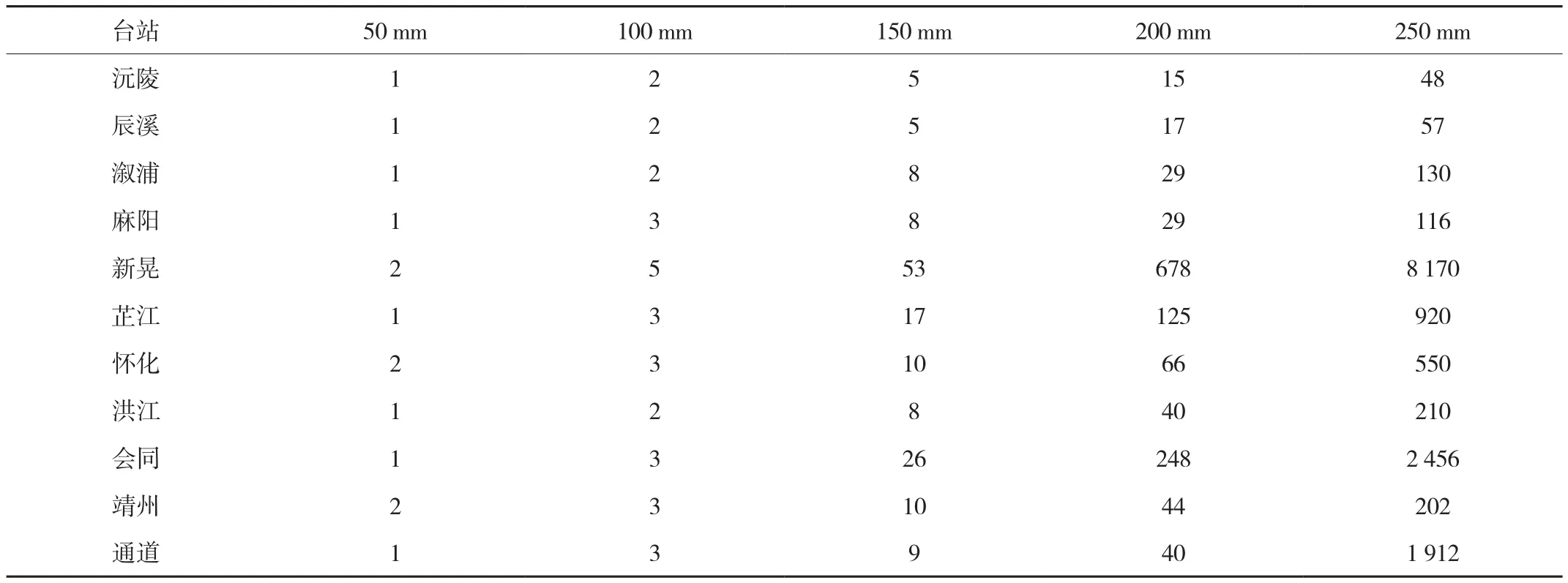
表3　怀化地区各站给定不同最大日降雨量求重现期的理论值 　　年

2.3重现期值计算结果

重现期值计算结果（表4）。

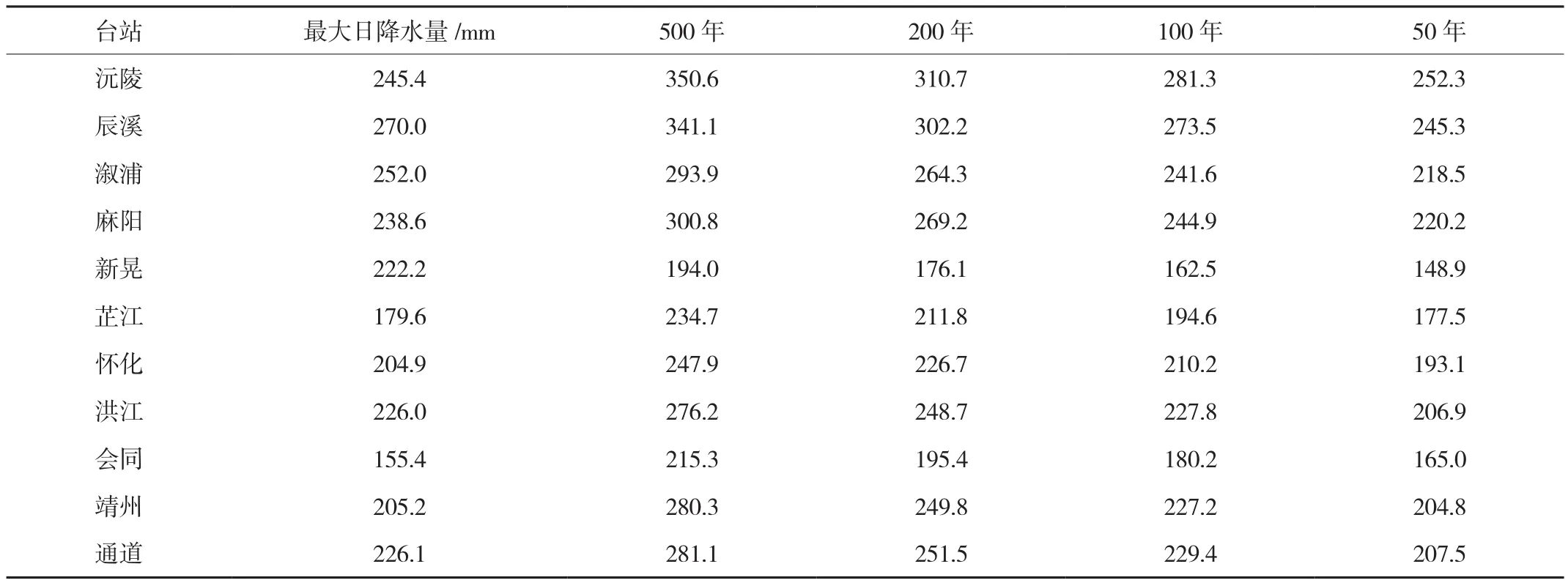
表4　怀化地区各站不同重现期的年最大日降雨量理论值 　mm

3　结论与讨论

（1）Pearson-Ⅲ分布﹑耿贝尔分布和对数正态分布均具有较好的拟合能力，可用来拟合年最大日降雨量的分布，进而求得不同降雨量的重现期。在怀化地区11个站的拟合中，有3个站用Pearson-Ⅲ型分布，2个站用耿贝尔分布，6个站用对数正态分布拟合最佳。

（2）对于不同量级降雨量的重现期，50mm的日降雨量基本上全市每年都会出现；100mm的日降雨量怀化地区北部2～3年出现1次，中部3～5年出现1次，而南部2～3年出现1次；250mm的日降雨量重现期，差别较大。

（3）从怀化地区各站不同重现期降水极值分布看，各地差异较大。怀化北部降水极值较大，南部次之，中部较小。其中，北部沅陵最大，中部的新晃最小。

（4）针对不同站点，用3种不同的概率分布方法进行拟合，并选取最佳拟合模型，对不同量级降雨量的重现期进行计算，且通过了显著性水平a=0.05的检验，计算值可应用于气象服务。

[1]魏生生，郭化文，陈建昌．国内外求可能最大降雨量研究的综述．气象科技，1998，27（1）：16～21

[2]马开玉．气候统计原理与分析方法．北京：气象出版社，1993：69～76

[3]林两位，王莉萍．用Pearson-Ⅲ概率分布推算重现期年最大日雨量．气象科技，2005，33（4）：314～317

[4]尹文有，郑皎，王继红，等．年最大日雨量极值分布拟合与推算．气象科技，2011，39（2）：137～140

*项目资助：湖南省气象局2016年短平快课题（XQKJ16B074）